人教版八上高分笔记之导与练12.3.2角的平分线的判定(原卷+答案)
文档属性
| 名称 | 人教版八上高分笔记之导与练12.3.2角的平分线的判定(原卷+答案) |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-09 22:01:36 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
12.3角的平分线的性质
角的平分线的判定
知识要点:
角的内部到角的两边的距离??
__的点在角的平分线上.
2.到三角形三边距离相等的点是三角形______________
易错点睛
如图,L1,L2,L3是三条两两相交的笔直公路,现欲修建一个加油站,使它到三条公路的距离相等,这个加油站的位置共有(?
??)
A.1处
B.2处
C.3处
D.4处
【点睛】??应考虑内角平分线的交点或内、外角平分线的交点。
典型例题:
题型一
角的平分线的判定及其应用
例1、如图,∠MON=60°,A,B分别为射线OM,ON上的动点(点A,B不与点0重合),在∠MON的内部,ΔAOB的外部有一点P,且AP=BP,∠APB=120°.求证:点P在∠MON的平分线上.
解题策略:利用角的平分线的判定定理时,一般过某一点作角的两边的垂线,即添加辅助线,这是解决此类问题的基本方法.
变式练习:
两块完全一样的三角尺按如图所示的方式摆放,它们的一组对应直角边分别在△ABC的边AB,AC上,且这组对应边所对的顶点重合于点M,则点M一定(
?)
在ZA的平分线上
B.在AC边的高上
C.在AB边的中线上???
D.以上都有可能
如图,已知AB//CD,AD⊥CD,AE⊥BC,∠DAC=35°,AD=AE,则∠B的度数为(
)
A.50°
B.60°
C.70°
D.80°
第2题
第3题
如图,在ΔABC中,0是ΔABC内一点,且点0到ΔABC三边的距离相等.若∠A=70°,则∠BOC=_____________
如图,已知D,E,F分别是ΔABC的三边上的点,CE=BF,且ΔDCE?的面积与ΔDBF的面积相等.求证:AD平分∠BAC.
题型二
角的平分线的性质与判定的综合应
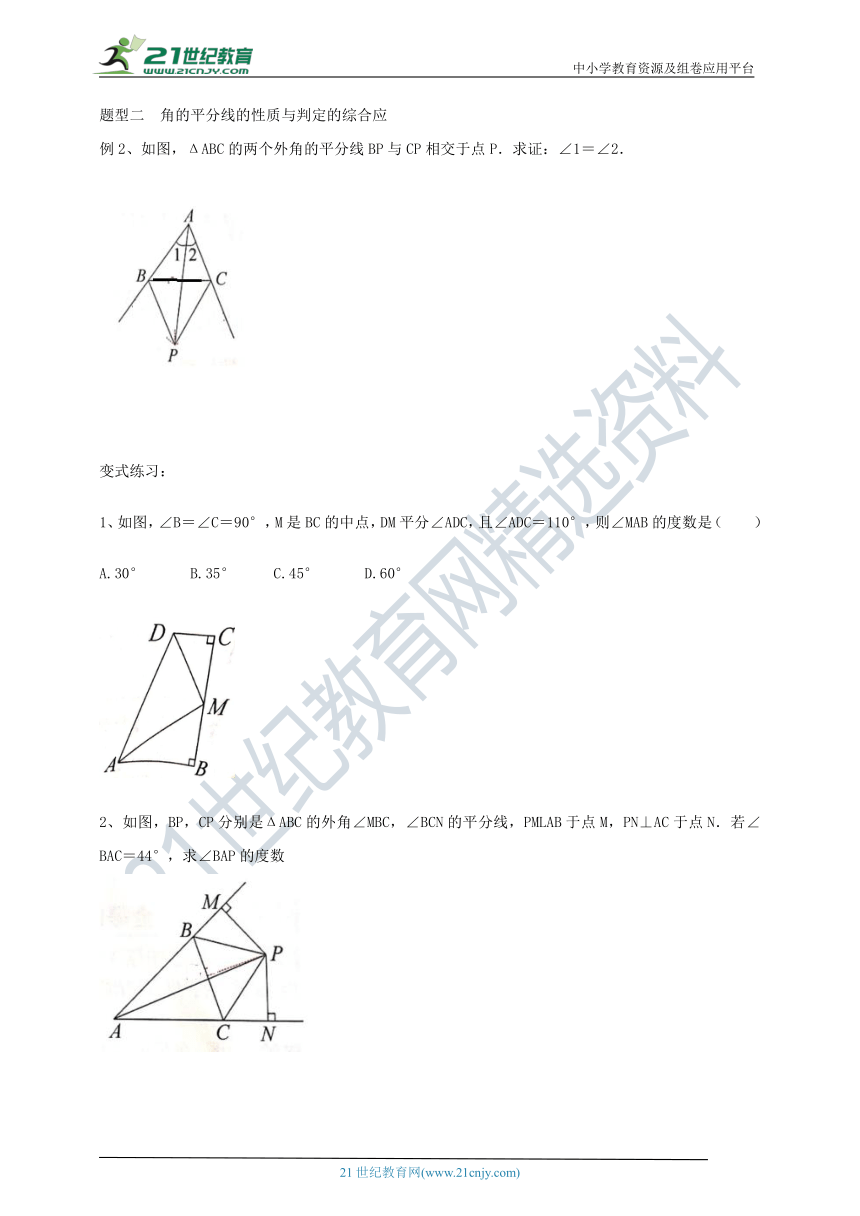
例2、如图,ΔABC的两个外角的平分线BP与CP相交于点P.求证:∠1=∠2.
变式练习:
1、如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB的度数是(
)
A.30°
B.35°
C.45°
D.60°
2、如图,BP,CP分别是ΔABC的外角∠MBC,∠BCN的平分线,PMLAB于点M,PN⊥AC于点N.若∠BAC=44°,求∠BAP的度数
基础练习:
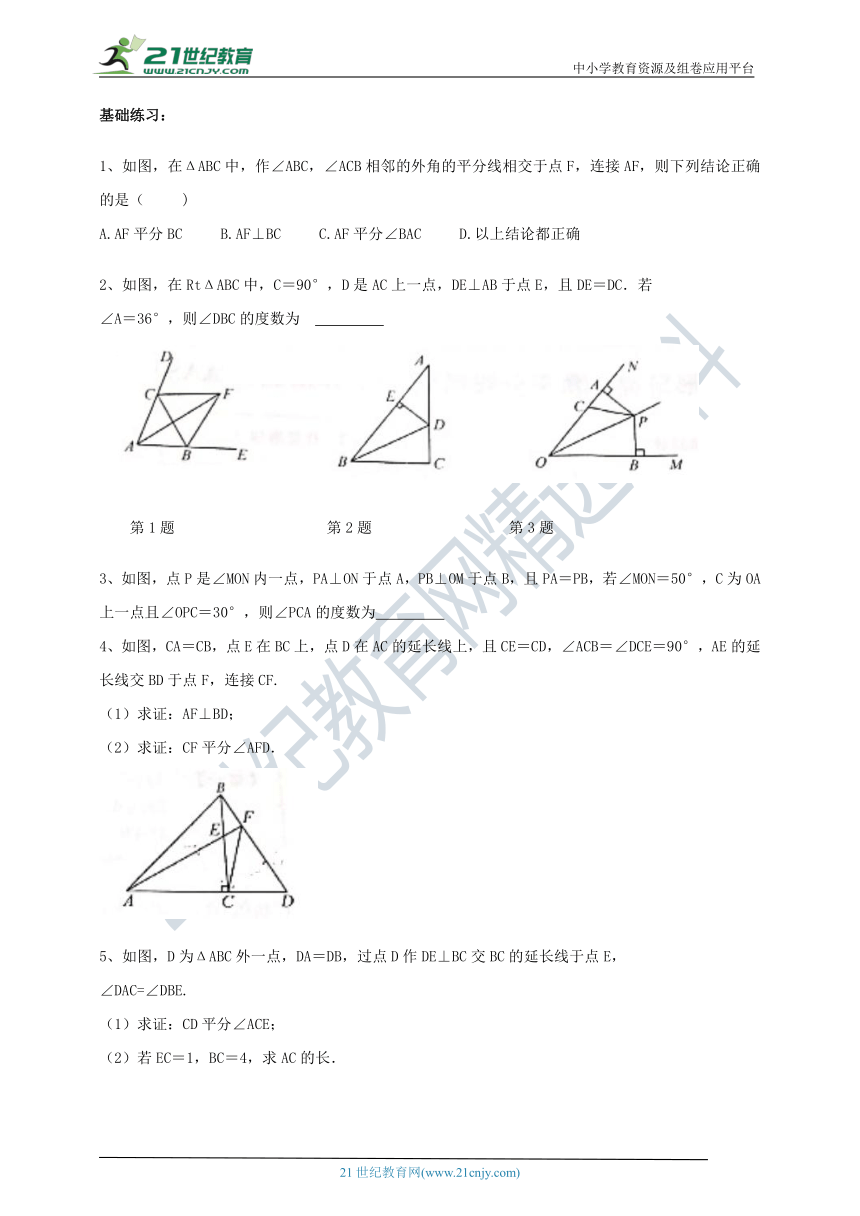
1、如图,在ΔABC中,作∠ABC,∠ACB相邻的外角的平分线相交于点F,连接AF,则下列结论正确的是(
?)?
A.AF平分BC
B.AF⊥BC
C.AF平分∠BAC
D.以上结论都正确
2、如图,在RtΔABC中,C=90°,D是AC上一点,DE⊥AB于点E,且DE=DC.若
∠A=36°,则∠DBC的度数为??
第1题
第2题
第3题
3、如图,点P是∠MON内一点,PA⊥ON于点A,PB⊥OM于点B,且PA=PB,若∠MON=50°,C为OA上一点且∠OPC=30°,则∠PCA的度数为?
4、如图,CA=CB,点E在BC上,点D在AC的延长线上,且CE=CD,∠ACB=∠DCE=90°,AE的延长线交BD于点F,连接CF.
(1)求证:AF⊥BD;
(2)求证:CF平分∠AFD.
5、如图,D为ΔABC外一点,DA=DB,过点D作DE⊥BC交BC的延长线于点E,
∠DAC=∠DBE.?
(1)求证:CD平分∠ACE;
(2)若EC=1,BC=4,求AC的长.
综合应用
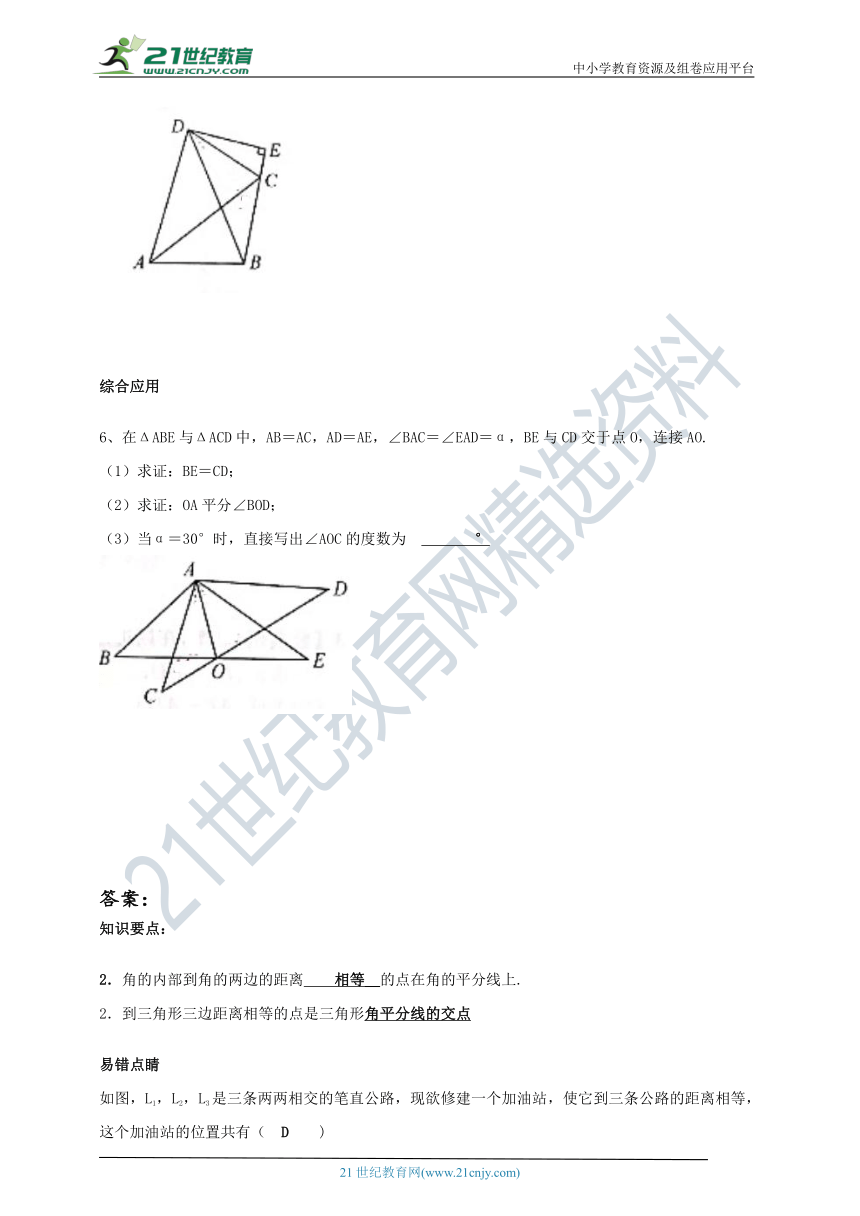
6、在ΔABE与ΔACD中,AB=AC,AD=AE,∠BAC=∠EAD=α,BE与CD交于点O,连接AO.?
(1)求证:BE=CD;
(2)求证:OA平分∠BOD;
(3)当α=30°时,直接写出∠AOC的度数为??
°
答案:
知识要点:
角的内部到角的两边的距离??相等__的点在角的平分线上.
2.到三角形三边距离相等的点是三角形角平分线的交点
易错点睛
如图,L1,L2,L3是三条两两相交的笔直公路,现欲修建一个加油站,使它到三条公路的距离相等,这个加油站的位置共有(?D??)
A.1处
B.2处
C.3处
D.4处
【点睛】??应考虑内角平分线的交点或内、外角平分线的交点。
典型例题:
题型一
角的平分线的判定及其应用
例1、如图,∠MON=60°,A,B分别为射线OM,ON上的动点(点A,B不与点0重合),在∠MON的内部,ΔAOB的外部有一点P,且AP=BP,∠APB=120°.求证:点P在∠MON的平分线上.
证明:如图,过点P分别作PC⊥⊥OM,PD⊥ON,垂足分别为C,D,则∠ACP=∠ODP=∠BDP=90°.
在四边形OCPD中,
∠CPD=360°-∠ACP-∠MON-∠ODP=360°-90°-60°-90°=120°.
∵∠APB=120°,∴∠APB=∠CPD.
∴∠CPD-∠APD=∠APB-∠APD,
即∠APC=∠BPD.
在ΔAPC和ΔBPD中,∠ACP=∠BDP,?∠APC=∠BPD,AP=BP,
∴ΔAPC≌ΔBPD(AAS)·∴PC=PD.
∴点P在∠MON的平分线上.
解题策略:利用角的平分线的判定定理时,一般过某一点作角的两边的垂线,即添加辅助线,这是解决此类问题的基本方法.
变式练习:
两块完全一样的三角尺按如图所示的方式摆放,它们的一组对应直角边分别在△ABC的边AB,AC上,且这组对应边所对的顶点重合于点M,则点M一定(
A?)
在ZA的平分线上
B.在AC边的高上
C.在AB边的中线上???
D.以上都有可能
如图,已知AB//CD,AD⊥CD,AE⊥BC,∠DAC=35°,AD=AE,则∠B的度数为(
C
)
A.50°
B.60°
C.70°
D.80°
第2题
第3题
如图,在ΔABC中,0是ΔABC内一点,且点0到ΔABC三边的距离相等.若∠A=70°,则∠BOC=125°
如图,已知D,E,F分别是ΔABC的三边上的点,CE=BF,且ΔDCE?的面积与ΔDBF的面积相等.求证:AD平分∠BAC.
证明:如图,过点D分别作DM⊥AB于点M,DN⊥AC于点N.
∵ΔDCE的面积与ΔDBF的面积相等,
CE·DN=BF·DM.
∵CE=BF,∴DN=DM.又DN⊥AC,DM⊥AB,∴AD平分∠BAC.?
题型二
角的平分线的性质与判定的综合应
例2、如图,ΔABC的两个外角的平分线BP与CP相交于点P.求证:∠1=∠2.
证明:如图,过点P分别作PE⊥AB的延长线于点E,PG⊥AC的延长线于点PH⊥BC于点H
∵BP是∠EBC的平分线,PE⊥AB,PH⊥BC,
∴PE=PH.同理可证PG=PH,∴PE=PG.
又PE⊥AB,PG⊥AC,∴AP是∠BAC的平分线.
∴∠1=∠2.
方法总结:有关角的平分线的几何问题中常见的添加辅助线的
方法:若OP为∠AOB的平分线,则:
(1)向角的另一边作垂线段,构造直角三角形,如图①;
(2)作对折线,即在OA上截取OC=0D,构造全等三角形,如图②.
变式练习:
1、如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB的度数是(
B
)
A.30°
B.35°
C.45°
D.60°
如图,BP,CP分别是ΔABC的外角∠MBC,∠BCN的平分线,PMLAB于点M,
PN⊥AC于点N.若∠BAC=44°,求∠BAP的度数
解:如图,过点P作PD⊥BC?于点D.?
∵BP是∠MBC的?平分线,PM⊥AB,PD⊥BC,?
∴PM=PD.同理,PN=PD,
∴PM=PN.
又PM⊥AB,PN⊥AC,∴AP平分∠BAC.
∴∠BAP=∠BAC=x44°=22°.
基础练习:
1、如图,在ΔABC中,作∠ABC,∠ACB相邻的外角的平分线相交于点F,连接AF,则下列结论正确的是(
C?)?
A.AF平分BC
B.AF⊥BC
C.AF平分∠BAC
D.以上结论都正确
2、如图,在RtΔABC中,C=90°,D是AC上一点,DE⊥AB于点E,且DE=DC.若
∠A=36°,则∠DBC的度数为??27°
第1题
第2题
第3题
3、如图,点P是∠MON内一点,PA⊥ON于点A,PB⊥OM于点B,且PA=PB,若∠MON=50°,C为OA上一点且∠OPC=30°,则∠PCA的度数为??55°
4、如图,CA=CB,点E在BC上,点D在AC的延长线上,且CE=CD,∠ACB=∠DCE=90°,AE的延长线交BD于点F,连接CF.
(1)求证:AF⊥BD;
(2)求证:CF平分∠AFD.
证明:(1)证ΔACE≌ΔBCD(SAS),∴∠CAE=∠CBD,
∴∠AFB=∠ACE=90°,∴AF⊥BD;?
(2)过点C分别作CM上AE于点M.CN⊥BD于点N,
证△ACM≌ΔBCN.∴CM=CN.∴.CF平分∠AFD.?
5、如图,D为ΔABC外一点,DA=DB,过点D作DE⊥BC交BC的延长线于点E,
∠DAC=∠DBE.?
(1)求证:CD平分∠ACE;
(2)若EC=1,BC=4,求AC的长.
(1)证明略
(2)在RtΔDCF与RtΔDCE中,DC=DC,?DE=DF,?
..RtΔDCF≌RtΔDCE(HL),∴CF=CE=1.?
∵ΔDAF≌ΔDBE,∴AF=BE=BC+CE=5,∴AC=AF+CF=6.
综合应用
6、在ΔABE与ΔACD中,AB=AC,AD=AE,∠BAC=∠EAD=α,BE与CD交于点O,连接AO.?
(1)求证:BE=CD;
(2)求证:OA平分∠BOD;
(3)当α=30°时,直接写出∠AOC的度数为??105°
解:(1)∵∠BAC=∠EAD,.∴∠BAC+∠CAE=∠EAD+∠CAE,
即∠BAE=∠CAD.在ΔABE与ΔACD中:
AB=AC,∠BAE=∠CAD.AE=AD.
∴ΔABE≌ΔACD(SAS),∴BE=CD;?
(2)过点A作AM⊥BE,AN⊥CD,垂足为M,N,则∠AMB=∠ANC=90°
∵ΔABE≌ΔACD,
∴∠B=∠C.?
在ΔABM与ΔACN中:∠B=∠C,∠AMB=∠ANC,AB=AC,∴ΔABM≌ΔACN(AAS),
∴AM=AN.
∵AM⊥BE.AN⊥CD,∴OA平分∠BOD;
(3)105°;
∵∠B=∠C.∴∠BOC=∠BAC=30°,∴∠BOD=150°.
∴OA平分∠BOD.
∴∠AOD=∠AOB=75°,∴∠AOC=∠AOB+∠BOC=105°.?
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
12.3角的平分线的性质
角的平分线的判定
知识要点:
角的内部到角的两边的距离??
__的点在角的平分线上.
2.到三角形三边距离相等的点是三角形______________
易错点睛
如图,L1,L2,L3是三条两两相交的笔直公路,现欲修建一个加油站,使它到三条公路的距离相等,这个加油站的位置共有(?
??)
A.1处
B.2处
C.3处
D.4处
【点睛】??应考虑内角平分线的交点或内、外角平分线的交点。
典型例题:
题型一
角的平分线的判定及其应用
例1、如图,∠MON=60°,A,B分别为射线OM,ON上的动点(点A,B不与点0重合),在∠MON的内部,ΔAOB的外部有一点P,且AP=BP,∠APB=120°.求证:点P在∠MON的平分线上.
解题策略:利用角的平分线的判定定理时,一般过某一点作角的两边的垂线,即添加辅助线,这是解决此类问题的基本方法.
变式练习:
两块完全一样的三角尺按如图所示的方式摆放,它们的一组对应直角边分别在△ABC的边AB,AC上,且这组对应边所对的顶点重合于点M,则点M一定(
?)
在ZA的平分线上
B.在AC边的高上
C.在AB边的中线上???
D.以上都有可能
如图,已知AB//CD,AD⊥CD,AE⊥BC,∠DAC=35°,AD=AE,则∠B的度数为(
)
A.50°
B.60°
C.70°
D.80°
第2题
第3题
如图,在ΔABC中,0是ΔABC内一点,且点0到ΔABC三边的距离相等.若∠A=70°,则∠BOC=_____________
如图,已知D,E,F分别是ΔABC的三边上的点,CE=BF,且ΔDCE?的面积与ΔDBF的面积相等.求证:AD平分∠BAC.
题型二
角的平分线的性质与判定的综合应
例2、如图,ΔABC的两个外角的平分线BP与CP相交于点P.求证:∠1=∠2.
变式练习:
1、如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB的度数是(
)
A.30°
B.35°
C.45°
D.60°
2、如图,BP,CP分别是ΔABC的外角∠MBC,∠BCN的平分线,PMLAB于点M,PN⊥AC于点N.若∠BAC=44°,求∠BAP的度数
基础练习:
1、如图,在ΔABC中,作∠ABC,∠ACB相邻的外角的平分线相交于点F,连接AF,则下列结论正确的是(
?)?
A.AF平分BC
B.AF⊥BC
C.AF平分∠BAC
D.以上结论都正确
2、如图,在RtΔABC中,C=90°,D是AC上一点,DE⊥AB于点E,且DE=DC.若
∠A=36°,则∠DBC的度数为??
第1题
第2题
第3题
3、如图,点P是∠MON内一点,PA⊥ON于点A,PB⊥OM于点B,且PA=PB,若∠MON=50°,C为OA上一点且∠OPC=30°,则∠PCA的度数为?
4、如图,CA=CB,点E在BC上,点D在AC的延长线上,且CE=CD,∠ACB=∠DCE=90°,AE的延长线交BD于点F,连接CF.
(1)求证:AF⊥BD;
(2)求证:CF平分∠AFD.
5、如图,D为ΔABC外一点,DA=DB,过点D作DE⊥BC交BC的延长线于点E,
∠DAC=∠DBE.?
(1)求证:CD平分∠ACE;
(2)若EC=1,BC=4,求AC的长.
综合应用
6、在ΔABE与ΔACD中,AB=AC,AD=AE,∠BAC=∠EAD=α,BE与CD交于点O,连接AO.?
(1)求证:BE=CD;
(2)求证:OA平分∠BOD;
(3)当α=30°时,直接写出∠AOC的度数为??
°
答案:
知识要点:
角的内部到角的两边的距离??相等__的点在角的平分线上.
2.到三角形三边距离相等的点是三角形角平分线的交点
易错点睛
如图,L1,L2,L3是三条两两相交的笔直公路,现欲修建一个加油站,使它到三条公路的距离相等,这个加油站的位置共有(?D??)
A.1处
B.2处
C.3处
D.4处
【点睛】??应考虑内角平分线的交点或内、外角平分线的交点。
典型例题:
题型一
角的平分线的判定及其应用
例1、如图,∠MON=60°,A,B分别为射线OM,ON上的动点(点A,B不与点0重合),在∠MON的内部,ΔAOB的外部有一点P,且AP=BP,∠APB=120°.求证:点P在∠MON的平分线上.
证明:如图,过点P分别作PC⊥⊥OM,PD⊥ON,垂足分别为C,D,则∠ACP=∠ODP=∠BDP=90°.
在四边形OCPD中,
∠CPD=360°-∠ACP-∠MON-∠ODP=360°-90°-60°-90°=120°.
∵∠APB=120°,∴∠APB=∠CPD.
∴∠CPD-∠APD=∠APB-∠APD,
即∠APC=∠BPD.
在ΔAPC和ΔBPD中,∠ACP=∠BDP,?∠APC=∠BPD,AP=BP,
∴ΔAPC≌ΔBPD(AAS)·∴PC=PD.
∴点P在∠MON的平分线上.
解题策略:利用角的平分线的判定定理时,一般过某一点作角的两边的垂线,即添加辅助线,这是解决此类问题的基本方法.
变式练习:
两块完全一样的三角尺按如图所示的方式摆放,它们的一组对应直角边分别在△ABC的边AB,AC上,且这组对应边所对的顶点重合于点M,则点M一定(
A?)
在ZA的平分线上
B.在AC边的高上
C.在AB边的中线上???
D.以上都有可能
如图,已知AB//CD,AD⊥CD,AE⊥BC,∠DAC=35°,AD=AE,则∠B的度数为(
C
)
A.50°
B.60°
C.70°
D.80°
第2题
第3题
如图,在ΔABC中,0是ΔABC内一点,且点0到ΔABC三边的距离相等.若∠A=70°,则∠BOC=125°
如图,已知D,E,F分别是ΔABC的三边上的点,CE=BF,且ΔDCE?的面积与ΔDBF的面积相等.求证:AD平分∠BAC.
证明:如图,过点D分别作DM⊥AB于点M,DN⊥AC于点N.
∵ΔDCE的面积与ΔDBF的面积相等,
CE·DN=BF·DM.
∵CE=BF,∴DN=DM.又DN⊥AC,DM⊥AB,∴AD平分∠BAC.?
题型二
角的平分线的性质与判定的综合应
例2、如图,ΔABC的两个外角的平分线BP与CP相交于点P.求证:∠1=∠2.
证明:如图,过点P分别作PE⊥AB的延长线于点E,PG⊥AC的延长线于点PH⊥BC于点H
∵BP是∠EBC的平分线,PE⊥AB,PH⊥BC,
∴PE=PH.同理可证PG=PH,∴PE=PG.
又PE⊥AB,PG⊥AC,∴AP是∠BAC的平分线.
∴∠1=∠2.
方法总结:有关角的平分线的几何问题中常见的添加辅助线的
方法:若OP为∠AOB的平分线,则:
(1)向角的另一边作垂线段,构造直角三角形,如图①;
(2)作对折线,即在OA上截取OC=0D,构造全等三角形,如图②.
变式练习:
1、如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB的度数是(
B
)
A.30°
B.35°
C.45°
D.60°
如图,BP,CP分别是ΔABC的外角∠MBC,∠BCN的平分线,PMLAB于点M,
PN⊥AC于点N.若∠BAC=44°,求∠BAP的度数
解:如图,过点P作PD⊥BC?于点D.?
∵BP是∠MBC的?平分线,PM⊥AB,PD⊥BC,?
∴PM=PD.同理,PN=PD,
∴PM=PN.
又PM⊥AB,PN⊥AC,∴AP平分∠BAC.
∴∠BAP=∠BAC=x44°=22°.
基础练习:
1、如图,在ΔABC中,作∠ABC,∠ACB相邻的外角的平分线相交于点F,连接AF,则下列结论正确的是(
C?)?
A.AF平分BC
B.AF⊥BC
C.AF平分∠BAC
D.以上结论都正确
2、如图,在RtΔABC中,C=90°,D是AC上一点,DE⊥AB于点E,且DE=DC.若
∠A=36°,则∠DBC的度数为??27°
第1题
第2题
第3题
3、如图,点P是∠MON内一点,PA⊥ON于点A,PB⊥OM于点B,且PA=PB,若∠MON=50°,C为OA上一点且∠OPC=30°,则∠PCA的度数为??55°
4、如图,CA=CB,点E在BC上,点D在AC的延长线上,且CE=CD,∠ACB=∠DCE=90°,AE的延长线交BD于点F,连接CF.
(1)求证:AF⊥BD;
(2)求证:CF平分∠AFD.
证明:(1)证ΔACE≌ΔBCD(SAS),∴∠CAE=∠CBD,
∴∠AFB=∠ACE=90°,∴AF⊥BD;?
(2)过点C分别作CM上AE于点M.CN⊥BD于点N,
证△ACM≌ΔBCN.∴CM=CN.∴.CF平分∠AFD.?
5、如图,D为ΔABC外一点,DA=DB,过点D作DE⊥BC交BC的延长线于点E,
∠DAC=∠DBE.?
(1)求证:CD平分∠ACE;
(2)若EC=1,BC=4,求AC的长.
(1)证明略
(2)在RtΔDCF与RtΔDCE中,DC=DC,?DE=DF,?
..RtΔDCF≌RtΔDCE(HL),∴CF=CE=1.?
∵ΔDAF≌ΔDBE,∴AF=BE=BC+CE=5,∴AC=AF+CF=6.
综合应用
6、在ΔABE与ΔACD中,AB=AC,AD=AE,∠BAC=∠EAD=α,BE与CD交于点O,连接AO.?
(1)求证:BE=CD;
(2)求证:OA平分∠BOD;
(3)当α=30°时,直接写出∠AOC的度数为??105°
解:(1)∵∠BAC=∠EAD,.∴∠BAC+∠CAE=∠EAD+∠CAE,
即∠BAE=∠CAD.在ΔABE与ΔACD中:
AB=AC,∠BAE=∠CAD.AE=AD.
∴ΔABE≌ΔACD(SAS),∴BE=CD;?
(2)过点A作AM⊥BE,AN⊥CD,垂足为M,N,则∠AMB=∠ANC=90°
∵ΔABE≌ΔACD,
∴∠B=∠C.?
在ΔABM与ΔACN中:∠B=∠C,∠AMB=∠ANC,AB=AC,∴ΔABM≌ΔACN(AAS),
∴AM=AN.
∵AM⊥BE.AN⊥CD,∴OA平分∠BOD;
(3)105°;
∵∠B=∠C.∴∠BOC=∠BAC=30°,∴∠BOD=150°.
∴OA平分∠BOD.
∴∠AOD=∠AOB=75°,∴∠AOC=∠AOB+∠BOC=105°.?
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
