11.1.2 三角形的高、中线与角平分线—人教版八年级数学上册课时作业(含答案)
文档属性
| 名称 | 11.1.2 三角形的高、中线与角平分线—人教版八年级数学上册课时作业(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 342.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版八年级数学上册课时作业
第十一章 三角形
11.1 与三角形有关的线段
11.1.2 三角形的高、中线与角平分线
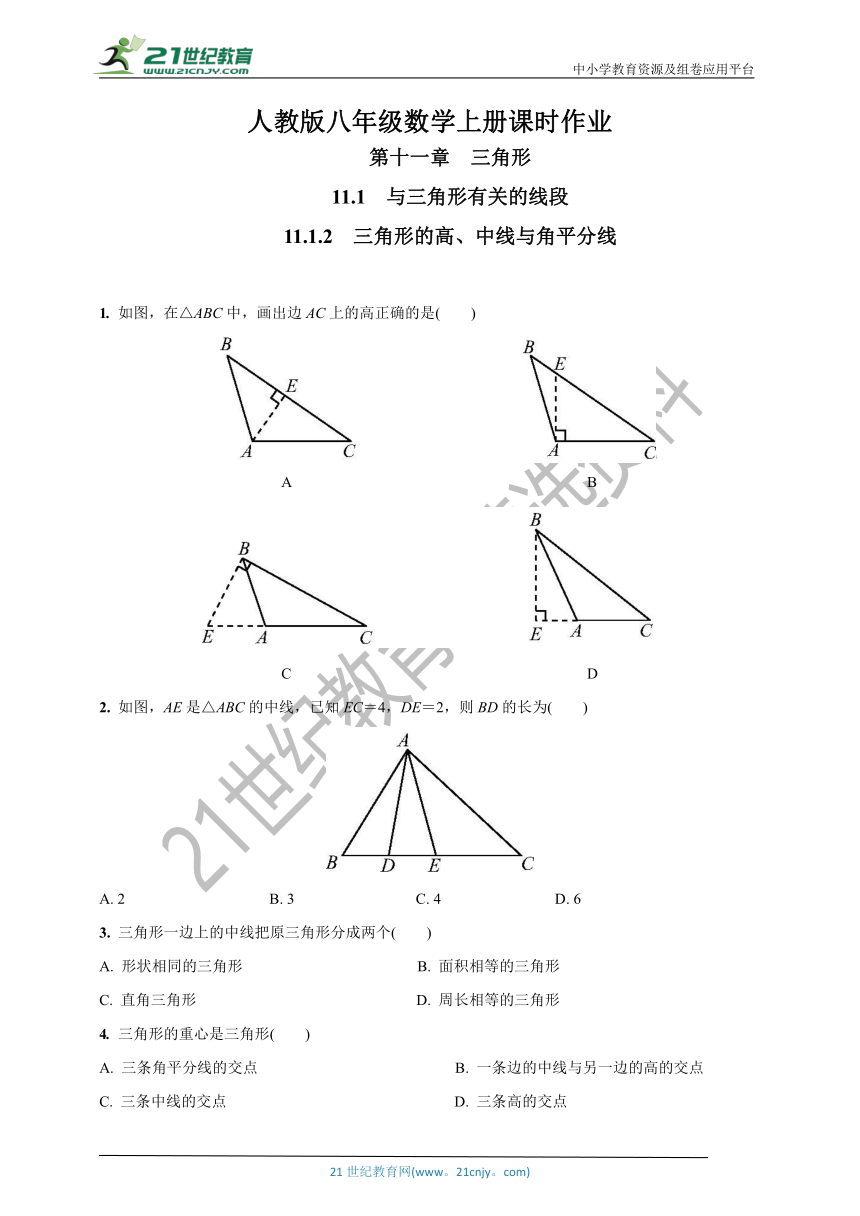
1. 如图,在△ABC中,画出边AC上的高正确的是( )
A B
C D
2. 如图,AE是△ABC的中线,已知EC=4,DE=2,则BD的长为( )
A. 2 B. 3 C. 4 D. 6
3. 三角形一边上的中线把原三角形分成两个( )
A. 形状相同的三角形 B. 面积相等的三角形
C. 直角三角形 D. 周长相等的三角形
4. 三角形的重心是三角形( )
A. 三条角平分线的交点 B. 一条边的中线与另一边的高的交点
C. 三条中线的交点 D. 三条高的交点
5. 如图,在△ABC中,AD为BC边上的中线,若AB=5 cm,AC=3 cm,则△ABD的周长比△ACD的周长多( )
A. 8 cm B. 5 cm C. 3 cm D. 2 cm
6. 如图,AD是△ABC的中线,已知△ABD的周长为22 cm,AB比AC长3 cm,则△ACD的周长为( )
A. 19 cm B. 22 cm C. 25 cm D. 31 cm
7. 下列说法正确的是( )
①三角形的角平分线是射线;②三角形的三条角平分线都在三角形内部,且交于同一点;③三角形的三条高都在三角形内部;④三角形的三条中线相交于一点.
A. ①② B. ②③ C. ③④ D. ②④
8. 若线段AP,AQ分别是△ABC边上的高和中线,则( )
A. AP>AQ B. AP≥AQ C. AP9. 如图,在△ABC中,∠C=90°,D,E是AC边上的两点,且AE=DE,BD平分∠EBC.那么下列说法中错误的有( )
①BE是△ABD的中线;②BD是△BCE的角平分线;③∠1=∠2=∠3;④BC是△ABE的高.
1个 B. 2个 C. 3个 D. 4个
10. 如图,在△ABC中,∠ABC=90°,BD⊥AC于点D,则BC边上的高是 ,AB边上的高是 ,AC边上的高是 .?
11. 若三角形三条高线的交点在三角形的一个顶点上,则此三角形是 .?
12. 如图,在△ABC中,已知点E,F分别是AD,CE边上的中点,且S△ABC=8 cm2,则S△BEF的值为 .?
13. 如图,在△ABC中,∠C=90°.
(1)分别指出图中BC,AC边上的高;
(2)画出AB边上的高CD;
(3)若BC=3,AC=4,AB=5,求AB边上的高CD的长.
14. 根据条件画图,并回答问题:
(1)画一个锐角△ABC(三边均不相等);
(2)作出BC边上的中线AE和高AD;
(3)写出两个以AD为高的三角形.
15. 如图,在△ABC中,AB=AC,P是BC边上的一点,PE⊥AC,PF⊥AB,CD是AB边上的高.若PE=5 cm,PF=3 cm,求CD的长.
16. 已知等腰三角形一腰上的中线将它的周长分为18 cm和30 cm两部分,求这个等腰三角形的各边长.
参考答案
1. D 2. A 3. B 4. C 5. D 6. A 7. D 8. D 9. A
10. AB BC BD
11. 直角三角形
12. 2 cm2
13. 解:(1)BC边上的高是AC,AC边上的高是BC.
(2)图略.
(3)∵S△ABC=AC·BC=AB·CD,∴CD=2.4.
14. 解:(1)如图所示,△ABC即为所求作的三角形.
(2)如图所示,过点A作AD⊥BC于点D,线段AD即为BC边上的高;取BC的中点E,连接AE,线段AE即为BC边上的中线.
(3)如图所示,以AD为高的三角形可以是△ABC,△ABD(答案不唯一).
15. 解:连接AP. ∵AB=AC,∴S△ABC=S△ABP+S△ACP=AB·PF+AC·PE=AB·CD,又∵AB=AC,∴PF+PE=CD. ∵PE=5 cm,PF=3 cm,∴CD=8 cm.
16. 解:设等腰三角形的腰长为x cm,底边长为y cm,则或 解得或 ∵12+12=24,∴此种情况不存在,∴此等腰三角形的腰长为20 cm,底边长为8 cm.
_21?????????è?????(www???21cnjy???com)_
人教版八年级数学上册课时作业
第十一章 三角形
11.1 与三角形有关的线段
11.1.2 三角形的高、中线与角平分线
1. 如图,在△ABC中,画出边AC上的高正确的是( )
A B
C D
2. 如图,AE是△ABC的中线,已知EC=4,DE=2,则BD的长为( )
A. 2 B. 3 C. 4 D. 6
3. 三角形一边上的中线把原三角形分成两个( )
A. 形状相同的三角形 B. 面积相等的三角形
C. 直角三角形 D. 周长相等的三角形
4. 三角形的重心是三角形( )
A. 三条角平分线的交点 B. 一条边的中线与另一边的高的交点
C. 三条中线的交点 D. 三条高的交点
5. 如图,在△ABC中,AD为BC边上的中线,若AB=5 cm,AC=3 cm,则△ABD的周长比△ACD的周长多( )
A. 8 cm B. 5 cm C. 3 cm D. 2 cm
6. 如图,AD是△ABC的中线,已知△ABD的周长为22 cm,AB比AC长3 cm,则△ACD的周长为( )
A. 19 cm B. 22 cm C. 25 cm D. 31 cm
7. 下列说法正确的是( )
①三角形的角平分线是射线;②三角形的三条角平分线都在三角形内部,且交于同一点;③三角形的三条高都在三角形内部;④三角形的三条中线相交于一点.
A. ①② B. ②③ C. ③④ D. ②④
8. 若线段AP,AQ分别是△ABC边上的高和中线,则( )
A. AP>AQ B. AP≥AQ C. AP
①BE是△ABD的中线;②BD是△BCE的角平分线;③∠1=∠2=∠3;④BC是△ABE的高.
1个 B. 2个 C. 3个 D. 4个
10. 如图,在△ABC中,∠ABC=90°,BD⊥AC于点D,则BC边上的高是 ,AB边上的高是 ,AC边上的高是 .?
11. 若三角形三条高线的交点在三角形的一个顶点上,则此三角形是 .?
12. 如图,在△ABC中,已知点E,F分别是AD,CE边上的中点,且S△ABC=8 cm2,则S△BEF的值为 .?
13. 如图,在△ABC中,∠C=90°.
(1)分别指出图中BC,AC边上的高;
(2)画出AB边上的高CD;
(3)若BC=3,AC=4,AB=5,求AB边上的高CD的长.
14. 根据条件画图,并回答问题:
(1)画一个锐角△ABC(三边均不相等);
(2)作出BC边上的中线AE和高AD;
(3)写出两个以AD为高的三角形.
15. 如图,在△ABC中,AB=AC,P是BC边上的一点,PE⊥AC,PF⊥AB,CD是AB边上的高.若PE=5 cm,PF=3 cm,求CD的长.
16. 已知等腰三角形一腰上的中线将它的周长分为18 cm和30 cm两部分,求这个等腰三角形的各边长.
参考答案
1. D 2. A 3. B 4. C 5. D 6. A 7. D 8. D 9. A
10. AB BC BD
11. 直角三角形
12. 2 cm2
13. 解:(1)BC边上的高是AC,AC边上的高是BC.
(2)图略.
(3)∵S△ABC=AC·BC=AB·CD,∴CD=2.4.
14. 解:(1)如图所示,△ABC即为所求作的三角形.
(2)如图所示,过点A作AD⊥BC于点D,线段AD即为BC边上的高;取BC的中点E,连接AE,线段AE即为BC边上的中线.
(3)如图所示,以AD为高的三角形可以是△ABC,△ABD(答案不唯一).
15. 解:连接AP. ∵AB=AC,∴S△ABC=S△ABP+S△ACP=AB·PF+AC·PE=AB·CD,又∵AB=AC,∴PF+PE=CD. ∵PE=5 cm,PF=3 cm,∴CD=8 cm.
16. 解:设等腰三角形的腰长为x cm,底边长为y cm,则或 解得或 ∵12+12=24,∴此种情况不存在,∴此等腰三角形的腰长为20 cm,底边长为8 cm.
_21?????????è?????(www???21cnjy???com)_
