北师大版七年级数学下册第五单元《生活中的轴对称》测试卷(word版含答案)
文档属性
| 名称 | 北师大版七年级数学下册第五单元《生活中的轴对称》测试卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 785.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 15:51:44 | ||
图片预览


文档简介
第五单元《生活中的轴对称》测试卷
一、选择题(本大题共14个小题,每题2分,共28分)
1.新版杭州市生活垃圾分类操作指南——《杭州市生活垃圾管理条例》从2019年8月15日开始施行.以下是几种垃圾分类的图标其中哪个图标是轴对称图形(
)
A.
B.
C.
D.
2.2020年的春节,对于所有人来说真的不一般.为了打好疫情攻坚战,医护人员在岗位上同时间赛跑,与病魔较量,而我们每个人都能为打赢这场仗贡献一份力量.勤洗手,戴口罩,少聚会,积极配合;防控工作,照顾好自己和家人,还有,说出一句简单的:中国加油!武汉加油!在“中国加油”这4个美术字中,可以看作轴对称图形的是( )
A.中
B.国
C.加
D.油
3.小天从镜子里看到镜子对面的电子钟如下图所示,则此时的实际时间是
(
)
A.21:10
B.10:21
C.10:51
D.12:01
4.如图是一个经过改造的规则为的台球桌面示意图,图中四个角上的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出(球可以经过台球边缘多次反弹),那么球最后将落入的球袋是(
)
A.1号袋
B.2号袋
C.3号袋
D.4号袋
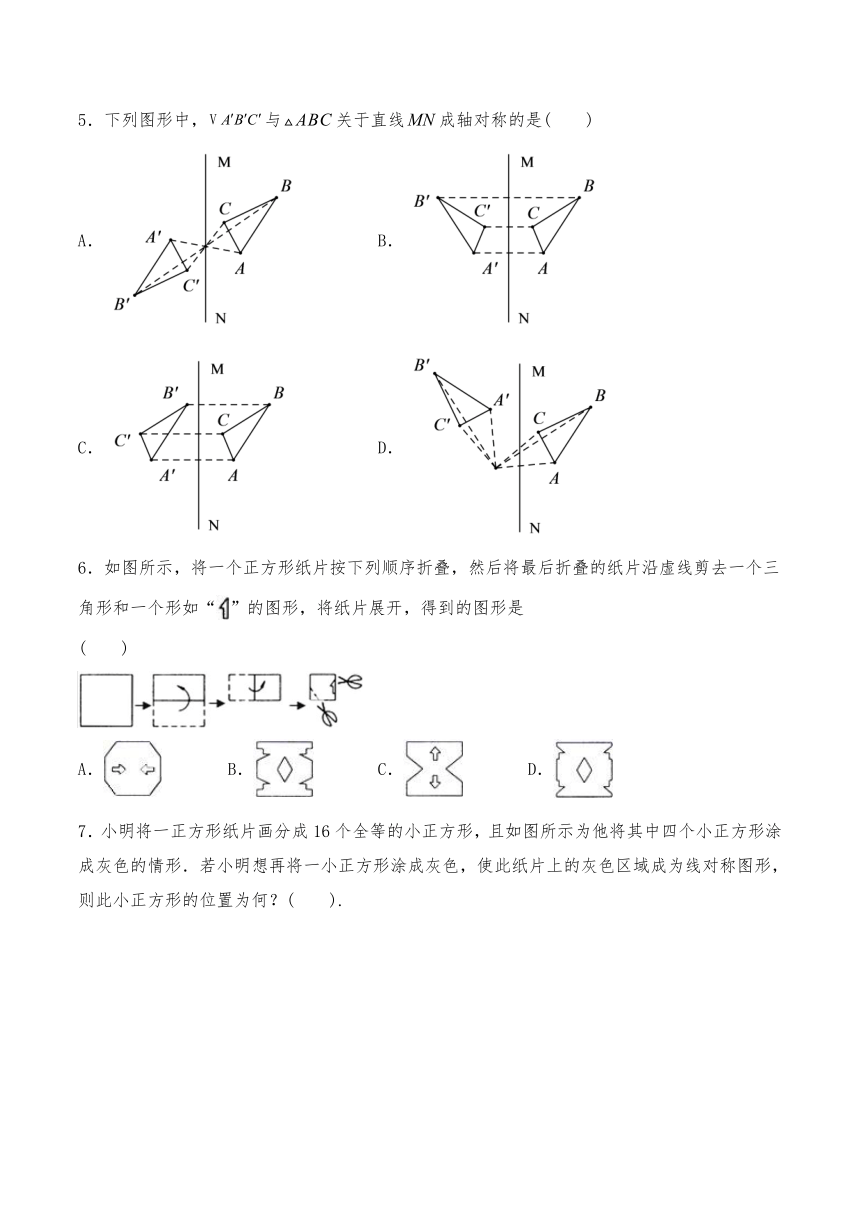
5.下列图形中,与关于直线成轴对称的是(
)
A.
B.
C.
D.
6.如图所示,将一个正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去一个三角形和一个形如“”的图形,将纸片展开,得到的图形是
( )
A.
B.
C.
D.
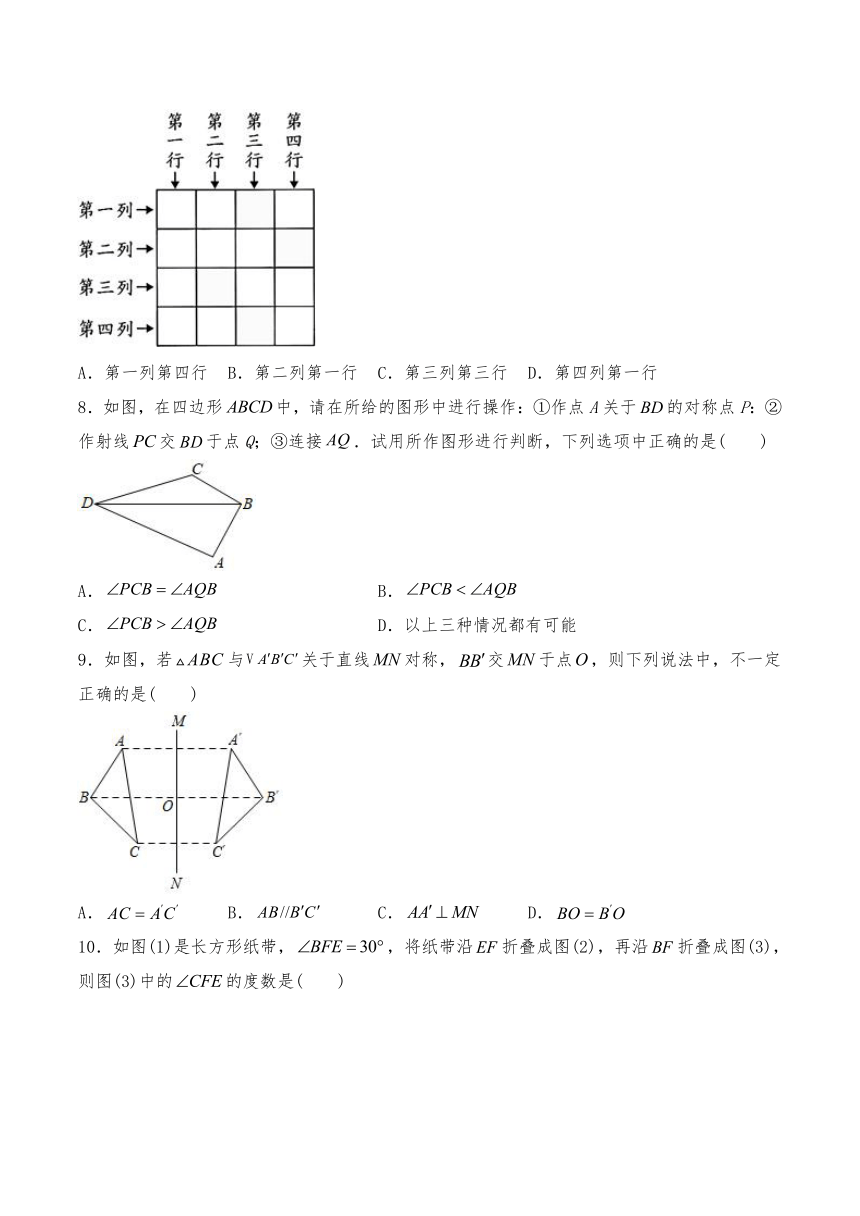
7.小明将一正方形纸片画分成16个全等的小正方形,且如图所示为他将其中四个小正方形涂成灰色的情形.若小明想再将一小正方形涂成灰色,使此纸片上的灰色区域成为线对称图形,则此小正方形的位置为何?(
).
A.第一列第四行
B.第二列第一行
C.第三列第三行
D.第四列第一行
8.如图,在四边形中,请在所给的图形中进行操作:①作点A关于的对称点P:②作射线交于点Q;③连接.试用所作图形进行判断,下列选项中正确的是(
)
A.
B.
C.
D.以上三种情况都有可能
9.如图,若与关于直线对称,交于点,则下列说法中,不一定正确的是(
)
A.
B.
C.
D.
10.如图(1)是长方形纸带,,将纸带沿折叠成图(2),再沿折叠成图(3),则图(3)中的的度数是(
)
A.120°
B.110°
C.100°
D.90°
11.如图,有一张四边形纸片ABCD,AD∥BC,将它沿GH折叠,使点D落在AB边上的点E处,点C落在点Q处,若∠GHB=80°,则∠AGE的度数为( )
A.20°
B.30°
C.35°
D.40°
12.如图,在的正方形格纸中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中是一个格点三角形,在这个的正方形格纸中,与成轴对称的格点三角形最多有( )
A.3个
B.4个
C.5个
D.6个
13.如图,直线是一条河,、是两个新农村定居点.欲在上的某点处修建一个水泵站,直接向、两地供水.现有如下四种管道铺设方案,图中实线表示铺设的供水管道,则铺设管道最短的方案是(
)
A.
B.
C.
D.
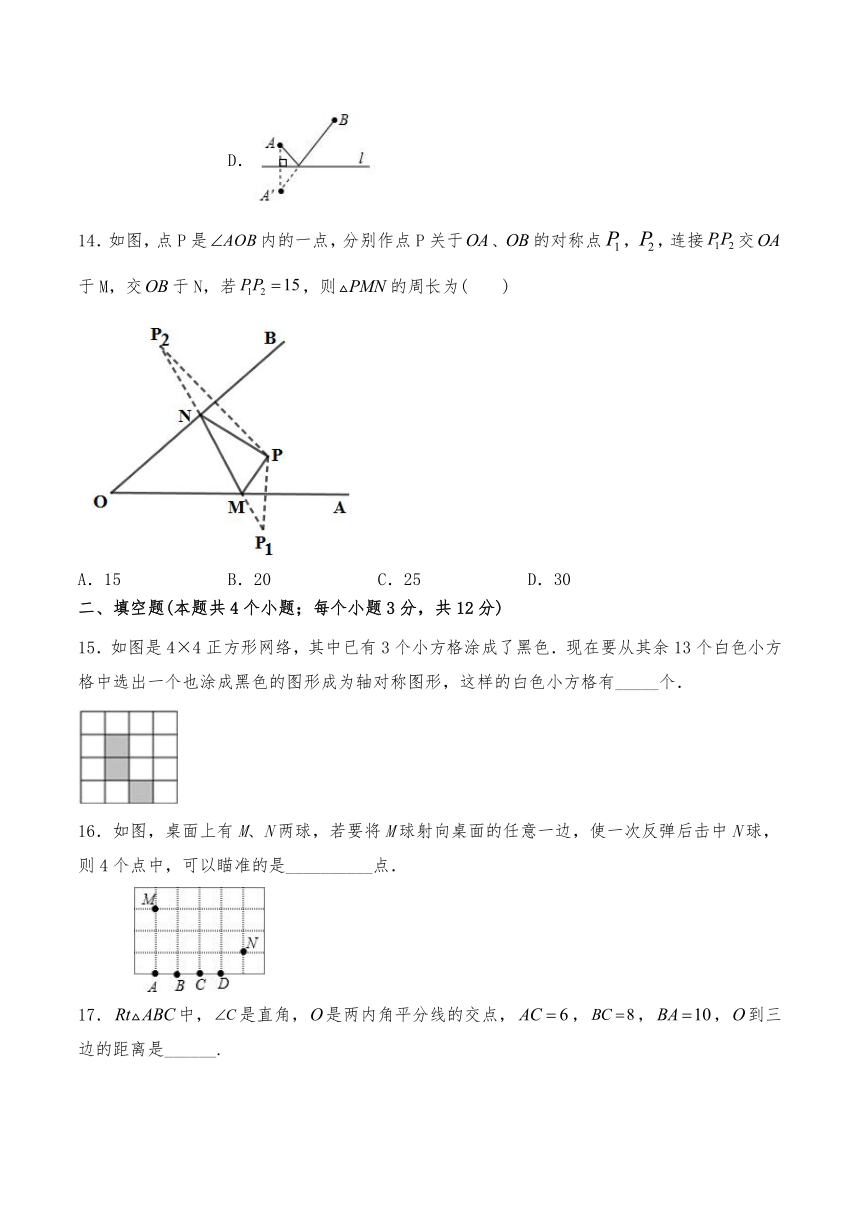
14.如图,点P是内的一点,分别作点P关于、的对称点,,连接交于M,交于N,若,则的周长为(
)
A.15
B.20
C.25
D.30
二、填空题(本题共4个小题;每个小题3分,共12分)
15.如图是4×4正方形网络,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色的图形成为轴对称图形,这样的白色小方格有_____个.
16.如图,桌面上有M、N两球,若要将M球射向桌面的任意一边,使一次反弹后击中N球,则4个点中,可以瞄准的是__________点.
17.中,是直角,是两内角平分线的交点,,,,到三边的距离是______.
18.如图,在等腰三角形ABC中,BC=3
cm,△ABC的面积是9
cm2,腰AB的垂直平分线EF交AC于点F,若点D为BC边上的中点,M为EF上的动点,则BM+DM的最小值为____.
三、解答题(本题共8道题,19-21每题6分,22-25每题8分,26题10分,满分60分)
19.如图,在3×3的正方形格纸中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中△是一个格点三角形.在每张图中画出一个与△成轴对称的格点三角形,并将所画三角形涂上阴影.
20.如图,△ABC和△ADE关于直线l对称,已知AB=15,DE=10,∠D=70°.求∠B的度数及BC、AD的长度
21.作图题(1)如图1,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
①在图中画出与△ABC关于直线l成轴对称的△AB′C′;
②在直线l上找一点P,使PB+PC的长最短.
(2)利用网格(图2)作图,请你先在图中的BC边上找一点P,使点P到边AB、AC的距离相等,再在射线AP上找一点Q,使QB=QC.
22.(教材呈现)数学课上,赵老师用无刻度的直尺和圆规按照华师版教材八年级上册87页完成角平分线的作法,方法如下:
试一试
如图,为已知角,试按下列步骤用直尺和圆规准确地作出的平分线.
第一步:在射线OA、OB上,分别截取OD、OE,使
第二步:分别以点D和点E为圆心,适当长(大于线段DE长的一半)为半径作圆弧,在内,两弧交于点C;
第三步:作射线OC.射线OC就是所要求作的的平分线
(问题1)赵老师用尺规作角平分线时,用到的三角形全等的判定方法是__________________.
(问题2)小明发现只利用直角三角板也可以作的角平分线,方法如下:
步骤:①利用三角板上的刻度,在OA、OB上分别截取OM、ON,使.
②分别过点M、N作OM、ON的垂线,交于点P.
③作射线OP,则OP为的平分线.
请根据小明的作法,求证OP为的平分线.
23.如图,已知△ABC.
(1)尺规作图:作∠ABC的角平分线交AC于点G(不写作法,保留作图痕迹);
(2)如果AB=8,BC=12,△ABG的面积为18,求△CBG的面积.
24.已知,如图,平分,,垂足为,点在的延长线上,,垂足为点,垂直平分,为垂足,连结,.
求证:.
25.如图,将△ABC
分别沿
AB,AC
翻折得到△ABD
和△AEC,线段
BD
与AE
交于点
F.
(1)若∠ABC=16?,∠ACB=30°,求∠DAE
及∠BFE
的值;
(2)若
BD
与
CE
所在的直线互相垂直,求∠CAB
的度数.
26.如果两个角之差的绝对值等于,则称这两个角互为“互优角”,即若,则称和互为“互优角”(本题中所有角都是大于且小于的角)
图1
图2
图3
(1)若和互为“互优角”,当时,则________;
(2)如图1,将一长方形纸片沿着对折,(点在线段上,点在线段上),使点落在,若与互为“互优角”,则的度数为________;
(3)再将纸片沿着对折(点在线段或上),使点落在.
①如图2,若点,,在同一直线上,且与互为“互优角”,求的度数(对折时,线段落在内部);
②若与互为“互优角”,则与应满足什么样的数量关系(直接写出结果即可).
答案
一、选择题
1.D.2.A.3.C.4.D.5.B.6.D.7.B.8.C.9.B.
10.D.11.A.12.D.13.D.14.A
二、填空题
15.4
16.D
17.2
18.6
三、解答题
19.解:如图:
20.
解:∵△ABC和△ADE关于直线l对称,
∴AB=AD,BC=DE,∠B=∠D
又∵AB=15,DE=10,∠D=70°
∴∠B=70°,BC=10,AD=15,
答:∠B=70°,BC=10、AD=15.
21.
解:(1)①如图1所示:△AB′C′即为所求;
②如图所示:P点即为所求,PB+PC的长为BC′的长,
(2)点P、Q如图2所示.
22.
解:问题1:张老师用尺规作角平分线时,用到的三角形全等的判定方法是SSS,
故答案为:SSS;
问题2:由作图得:
,,.
∴.
∴和是直角三角形.
∵,
∴.
∴.
∴OP为的平分线.
23.解:(1)如图,BG即为所求;
(2)如图,∵BG平分∠ABC,
过点G作GD⊥AB于点D,GE⊥BC于点E,
∴GD=GE,
∵AB=8,△ABG的面积为18,
∴
∴GD=,
∵BC=12,GE=GD=,
∴△CBG的面积为12×=27.
24.
证明:平分,,,
,
垂直平分,
,
,,
,
在和中,
.
25.
解:(1)∵∠ABC=16°,∠ACB=30°,
∴∠BAC=134°,
∵△ABC≌△ABD,△ABC≌△AEC,
∴∠BAD=∠EAC=134°;∠DAE=134°×3-360°=42°.
∵∠D=∠ACB=30°,
∴∠BFE=∠DFA=180°-42°-30°=108°;
(2)∵BD
所在直线与
CE
所在直线互相垂直,
∴∠DBC+∠ECB=90°,
∵翻折
∴∠ABC=∠DBC
∠ACB
=∠ECB
∴∠ABC+∠ACB=
(
∠DBC+∠ECB
)=45°,
∴∠CAB=180°-(∠ABC+∠ACB
)=
135°.
26.
解:(1)∵∠1和∠2互为“互优角”,∠1=90°,
∴|∠1-∠2|=60°,
∴90°-∠2=60°或90°-∠2=-60°,
解得:∠2=30°或150°,
故答案为:30°或150°;
(2)∵∠EPB′与∠B′PC互为“互优角”,
当∠EPB′<∠B′PC时,∠B′PC-∠EPB′=60°,
∴∠B′PC=∠EPB′+60°,
∵△BEP翻折得△B'EP,
∴∠EPB=∠EPB',
∵∠EPB+∠EPB'+∠B′PC=180°,
∴∠EPB'+∠EPB'+∠EPB′+60°=180°,
解得:∠EPB′=40°;
当∠EPB′>∠B′PC时,∠EPB′-∠B′PC=60°,
同理可得∠EPB′=80°.
综上所述,∠EPB的值为40°或80°;
故答案为:40°或80°;
(3)①∵点E、C′、P在同一直线上,且∠B′PC′与∠EPF互为“互优角”,
∵对折时,线段落在内部
∴∠B′PC′<∠EPF,∠EPF-∠B′PC′=60°=∠B′PF,
∵∠BPE=∠B′PE=∠EPF-60°,∠FPC=∠EPF,
∴∠BPE+∠EPB′+∠B′PF+∠FPC=180°,
∴∠EPF-60°+∠EPF+∠EPF=180°,
解得∠EPF=80°;
②当点F在边CD上时,如图:
显然∠EPF>∠B′PC′,
∵∠B′PC′与∠EPF互为“互优角”,
∴∠EPF-∠B′P′C=60°,
根据折叠的性质:∠B′PE=∠1,∠FPC′=∠2,
∴∠EPF=∠1+∠2+∠B′P′C,
∴∠EPF-∠B′P′C=∠1+∠2+∠B′P′C-∠B′P′C=∠1+∠2=60°,
即∠BPE+∠CPF=60°;
当点F在边AD上,且当∠EPF>∠B′PC′时,如图:
∠B′PC′与∠EPF互为“互优角”,
∴∠EPF-∠B′P′C
=60°,
根据折叠的性质:∠B′PE=∠1,∠FPC′=∠2,
∴∠EPF=∠1+∠2-∠B′P′C,
∴∠EPF-∠B′P′C
=∠1+∠2-2∠B′P′C
=60°,
∠1+∠EPF+∠2=∠1+∠1+∠2-∠B′P′C+∠2=2(∠1+∠2)
-∠B′P′C=180°,
解得:∠1+∠2=100°,
即∠BPE+∠CPF=100°;
当点F在边AD上,且当∠EPF<∠B′PC′时,如图:
∠B′PC′与∠EPF互为“互优角”,
∴∠B′P′C-∠EPF
=60°,
根据折叠的性质:∠B′PE=∠1,∠FPC′=∠2,
∴∠EPF=∠1+∠2-∠B′P′C,
∴∠B′P′C-∠EPF
=∠1+∠2-2∠EPF
=60°,
∠1+∠EPF+∠2=180°,
解得:∠1+∠2=140°,
即∠BPE+∠CPF=140°;
故∠BPE+∠CPF的度数为60°或100°或140°.
一、选择题(本大题共14个小题,每题2分,共28分)
1.新版杭州市生活垃圾分类操作指南——《杭州市生活垃圾管理条例》从2019年8月15日开始施行.以下是几种垃圾分类的图标其中哪个图标是轴对称图形(
)
A.
B.
C.
D.
2.2020年的春节,对于所有人来说真的不一般.为了打好疫情攻坚战,医护人员在岗位上同时间赛跑,与病魔较量,而我们每个人都能为打赢这场仗贡献一份力量.勤洗手,戴口罩,少聚会,积极配合;防控工作,照顾好自己和家人,还有,说出一句简单的:中国加油!武汉加油!在“中国加油”这4个美术字中,可以看作轴对称图形的是( )
A.中
B.国
C.加
D.油
3.小天从镜子里看到镜子对面的电子钟如下图所示,则此时的实际时间是
(
)
A.21:10
B.10:21
C.10:51
D.12:01
4.如图是一个经过改造的规则为的台球桌面示意图,图中四个角上的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出(球可以经过台球边缘多次反弹),那么球最后将落入的球袋是(
)
A.1号袋
B.2号袋
C.3号袋
D.4号袋
5.下列图形中,与关于直线成轴对称的是(
)
A.
B.
C.
D.
6.如图所示,将一个正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去一个三角形和一个形如“”的图形,将纸片展开,得到的图形是
( )
A.
B.
C.
D.
7.小明将一正方形纸片画分成16个全等的小正方形,且如图所示为他将其中四个小正方形涂成灰色的情形.若小明想再将一小正方形涂成灰色,使此纸片上的灰色区域成为线对称图形,则此小正方形的位置为何?(
).
A.第一列第四行
B.第二列第一行
C.第三列第三行
D.第四列第一行
8.如图,在四边形中,请在所给的图形中进行操作:①作点A关于的对称点P:②作射线交于点Q;③连接.试用所作图形进行判断,下列选项中正确的是(
)
A.
B.
C.
D.以上三种情况都有可能
9.如图,若与关于直线对称,交于点,则下列说法中,不一定正确的是(
)
A.
B.
C.
D.
10.如图(1)是长方形纸带,,将纸带沿折叠成图(2),再沿折叠成图(3),则图(3)中的的度数是(
)
A.120°
B.110°
C.100°
D.90°
11.如图,有一张四边形纸片ABCD,AD∥BC,将它沿GH折叠,使点D落在AB边上的点E处,点C落在点Q处,若∠GHB=80°,则∠AGE的度数为( )
A.20°
B.30°
C.35°
D.40°
12.如图,在的正方形格纸中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中是一个格点三角形,在这个的正方形格纸中,与成轴对称的格点三角形最多有( )
A.3个
B.4个
C.5个
D.6个
13.如图,直线是一条河,、是两个新农村定居点.欲在上的某点处修建一个水泵站,直接向、两地供水.现有如下四种管道铺设方案,图中实线表示铺设的供水管道,则铺设管道最短的方案是(
)
A.
B.
C.
D.
14.如图,点P是内的一点,分别作点P关于、的对称点,,连接交于M,交于N,若,则的周长为(
)
A.15
B.20
C.25
D.30
二、填空题(本题共4个小题;每个小题3分,共12分)
15.如图是4×4正方形网络,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色的图形成为轴对称图形,这样的白色小方格有_____个.
16.如图,桌面上有M、N两球,若要将M球射向桌面的任意一边,使一次反弹后击中N球,则4个点中,可以瞄准的是__________点.
17.中,是直角,是两内角平分线的交点,,,,到三边的距离是______.
18.如图,在等腰三角形ABC中,BC=3
cm,△ABC的面积是9
cm2,腰AB的垂直平分线EF交AC于点F,若点D为BC边上的中点,M为EF上的动点,则BM+DM的最小值为____.
三、解答题(本题共8道题,19-21每题6分,22-25每题8分,26题10分,满分60分)
19.如图,在3×3的正方形格纸中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中△是一个格点三角形.在每张图中画出一个与△成轴对称的格点三角形,并将所画三角形涂上阴影.
20.如图,△ABC和△ADE关于直线l对称,已知AB=15,DE=10,∠D=70°.求∠B的度数及BC、AD的长度
21.作图题(1)如图1,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
①在图中画出与△ABC关于直线l成轴对称的△AB′C′;
②在直线l上找一点P,使PB+PC的长最短.
(2)利用网格(图2)作图,请你先在图中的BC边上找一点P,使点P到边AB、AC的距离相等,再在射线AP上找一点Q,使QB=QC.
22.(教材呈现)数学课上,赵老师用无刻度的直尺和圆规按照华师版教材八年级上册87页完成角平分线的作法,方法如下:
试一试
如图,为已知角,试按下列步骤用直尺和圆规准确地作出的平分线.
第一步:在射线OA、OB上,分别截取OD、OE,使
第二步:分别以点D和点E为圆心,适当长(大于线段DE长的一半)为半径作圆弧,在内,两弧交于点C;
第三步:作射线OC.射线OC就是所要求作的的平分线
(问题1)赵老师用尺规作角平分线时,用到的三角形全等的判定方法是__________________.
(问题2)小明发现只利用直角三角板也可以作的角平分线,方法如下:
步骤:①利用三角板上的刻度,在OA、OB上分别截取OM、ON,使.
②分别过点M、N作OM、ON的垂线,交于点P.
③作射线OP,则OP为的平分线.
请根据小明的作法,求证OP为的平分线.
23.如图,已知△ABC.
(1)尺规作图:作∠ABC的角平分线交AC于点G(不写作法,保留作图痕迹);
(2)如果AB=8,BC=12,△ABG的面积为18,求△CBG的面积.
24.已知,如图,平分,,垂足为,点在的延长线上,,垂足为点,垂直平分,为垂足,连结,.
求证:.
25.如图,将△ABC
分别沿
AB,AC
翻折得到△ABD
和△AEC,线段
BD
与AE
交于点
F.
(1)若∠ABC=16?,∠ACB=30°,求∠DAE
及∠BFE
的值;
(2)若
BD
与
CE
所在的直线互相垂直,求∠CAB
的度数.
26.如果两个角之差的绝对值等于,则称这两个角互为“互优角”,即若,则称和互为“互优角”(本题中所有角都是大于且小于的角)
图1
图2
图3
(1)若和互为“互优角”,当时,则________;
(2)如图1,将一长方形纸片沿着对折,(点在线段上,点在线段上),使点落在,若与互为“互优角”,则的度数为________;
(3)再将纸片沿着对折(点在线段或上),使点落在.
①如图2,若点,,在同一直线上,且与互为“互优角”,求的度数(对折时,线段落在内部);
②若与互为“互优角”,则与应满足什么样的数量关系(直接写出结果即可).
答案
一、选择题
1.D.2.A.3.C.4.D.5.B.6.D.7.B.8.C.9.B.
10.D.11.A.12.D.13.D.14.A
二、填空题
15.4
16.D
17.2
18.6
三、解答题
19.解:如图:
20.
解:∵△ABC和△ADE关于直线l对称,
∴AB=AD,BC=DE,∠B=∠D
又∵AB=15,DE=10,∠D=70°
∴∠B=70°,BC=10,AD=15,
答:∠B=70°,BC=10、AD=15.
21.
解:(1)①如图1所示:△AB′C′即为所求;
②如图所示:P点即为所求,PB+PC的长为BC′的长,
(2)点P、Q如图2所示.
22.
解:问题1:张老师用尺规作角平分线时,用到的三角形全等的判定方法是SSS,
故答案为:SSS;
问题2:由作图得:
,,.
∴.
∴和是直角三角形.
∵,
∴.
∴.
∴OP为的平分线.
23.解:(1)如图,BG即为所求;
(2)如图,∵BG平分∠ABC,
过点G作GD⊥AB于点D,GE⊥BC于点E,
∴GD=GE,
∵AB=8,△ABG的面积为18,
∴
∴GD=,
∵BC=12,GE=GD=,
∴△CBG的面积为12×=27.
24.
证明:平分,,,
,
垂直平分,
,
,,
,
在和中,
.
25.
解:(1)∵∠ABC=16°,∠ACB=30°,
∴∠BAC=134°,
∵△ABC≌△ABD,△ABC≌△AEC,
∴∠BAD=∠EAC=134°;∠DAE=134°×3-360°=42°.
∵∠D=∠ACB=30°,
∴∠BFE=∠DFA=180°-42°-30°=108°;
(2)∵BD
所在直线与
CE
所在直线互相垂直,
∴∠DBC+∠ECB=90°,
∵翻折
∴∠ABC=∠DBC
∠ACB
=∠ECB
∴∠ABC+∠ACB=
(
∠DBC+∠ECB
)=45°,
∴∠CAB=180°-(∠ABC+∠ACB
)=
135°.
26.
解:(1)∵∠1和∠2互为“互优角”,∠1=90°,
∴|∠1-∠2|=60°,
∴90°-∠2=60°或90°-∠2=-60°,
解得:∠2=30°或150°,
故答案为:30°或150°;
(2)∵∠EPB′与∠B′PC互为“互优角”,
当∠EPB′<∠B′PC时,∠B′PC-∠EPB′=60°,
∴∠B′PC=∠EPB′+60°,
∵△BEP翻折得△B'EP,
∴∠EPB=∠EPB',
∵∠EPB+∠EPB'+∠B′PC=180°,
∴∠EPB'+∠EPB'+∠EPB′+60°=180°,
解得:∠EPB′=40°;
当∠EPB′>∠B′PC时,∠EPB′-∠B′PC=60°,
同理可得∠EPB′=80°.
综上所述,∠EPB的值为40°或80°;
故答案为:40°或80°;
(3)①∵点E、C′、P在同一直线上,且∠B′PC′与∠EPF互为“互优角”,
∵对折时,线段落在内部
∴∠B′PC′<∠EPF,∠EPF-∠B′PC′=60°=∠B′PF,
∵∠BPE=∠B′PE=∠EPF-60°,∠FPC=∠EPF,
∴∠BPE+∠EPB′+∠B′PF+∠FPC=180°,
∴∠EPF-60°+∠EPF+∠EPF=180°,
解得∠EPF=80°;
②当点F在边CD上时,如图:
显然∠EPF>∠B′PC′,
∵∠B′PC′与∠EPF互为“互优角”,
∴∠EPF-∠B′P′C=60°,
根据折叠的性质:∠B′PE=∠1,∠FPC′=∠2,
∴∠EPF=∠1+∠2+∠B′P′C,
∴∠EPF-∠B′P′C=∠1+∠2+∠B′P′C-∠B′P′C=∠1+∠2=60°,
即∠BPE+∠CPF=60°;
当点F在边AD上,且当∠EPF>∠B′PC′时,如图:
∠B′PC′与∠EPF互为“互优角”,
∴∠EPF-∠B′P′C
=60°,
根据折叠的性质:∠B′PE=∠1,∠FPC′=∠2,
∴∠EPF=∠1+∠2-∠B′P′C,
∴∠EPF-∠B′P′C
=∠1+∠2-2∠B′P′C
=60°,
∠1+∠EPF+∠2=∠1+∠1+∠2-∠B′P′C+∠2=2(∠1+∠2)
-∠B′P′C=180°,
解得:∠1+∠2=100°,
即∠BPE+∠CPF=100°;
当点F在边AD上,且当∠EPF<∠B′PC′时,如图:
∠B′PC′与∠EPF互为“互优角”,
∴∠B′P′C-∠EPF
=60°,
根据折叠的性质:∠B′PE=∠1,∠FPC′=∠2,
∴∠EPF=∠1+∠2-∠B′P′C,
∴∠B′P′C-∠EPF
=∠1+∠2-2∠EPF
=60°,
∠1+∠EPF+∠2=180°,
解得:∠1+∠2=140°,
即∠BPE+∠CPF=140°;
故∠BPE+∠CPF的度数为60°或100°或140°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
