八年级数学上册试题 一课一练11.3 《多边形及其内角和》习题1-人教版(word版含答案)
文档属性
| 名称 | 八年级数学上册试题 一课一练11.3 《多边形及其内角和》习题1-人教版(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 280.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 15:36:58 | ||
图片预览

文档简介
11.3
《多边形及其内角和》习题1
一、选择题
1.七边形的内角和是( )
A.360°
B.540°
C.720°
D.900°
2.若一个正多边形的一个外角为45°,则这个正多边形的边数是(
)
A.6
B.7
C.8
D.9
3.如图,2×5的正方形网格中,用5张1×2的矩形纸片将网格完全覆盖,则不同的覆盖方法有(
)
A.3种
B.5种
C.8种
D.13种
4.若多边形的内角和大于
900°,则该多边形的边数最小为(
)
A.9
B.8
C.7
D.6
5.一个多边形的内角和是720°,这个多边形是( )
A.五边形
B.六边形
C.七边形
D.八边形
6.一个多边形的内角和比它的外角和的2倍还大180°,这个多边形的边数为( )
A.7
B.8
C.9
D.10
7.如果一个多边形的内角和是外角和的5倍,那么这个多边形的边数是( )
A.10
B.11
C.12
D.13
8.将一个圆形纸片,如下图连续对折三次之后,用剪刀剪去其方形部分,展开后得到的多边形的内角和角度为(
)
A.180°
B.540°
C.1080°
D.2160°
9.一个多边形的每个内角都相等,并且它的一个外角与一个内角的比为1:3,则这个多边形为(
)
A.三角形
B.四边形
C.六边形
D.八边形
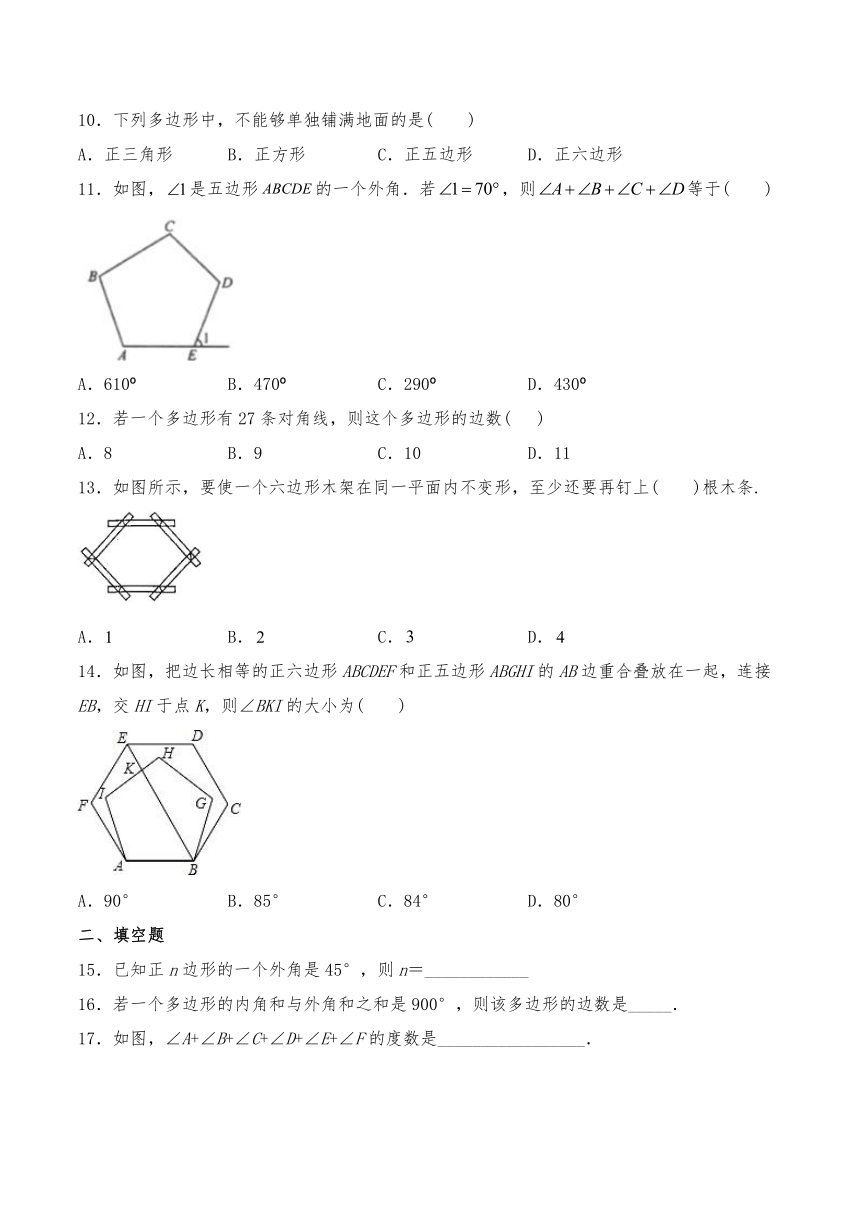
10.下列多边形中,不能够单独铺满地面的是( )
A.正三角形
B.正方形
C.正五边形
D.正六边形
11.如图,是五边形的一个外角.若,则等于(
)
A.610?
B.470?
C.290?
D.430?
12.若一个多边形有27条对角线,则这个多边形的边数(
)
A.8
B.9
C.10
D.11
13.如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上(
)根木条.
A.
B.
C.
D.
14.如图,把边长相等的正六边形ABCDEF和正五边形ABGHI的AB边重合叠放在一起,连接EB,交HI于点K,则∠BKI的大小为( )
A.90°
B.85°
C.84°
D.80°
二、填空题
15.已知正n边形的一个外角是45°,则n=____________
16.若一个多边形的内角和与外角和之和是900°,则该多边形的边数是_____.
17.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数是_________________.
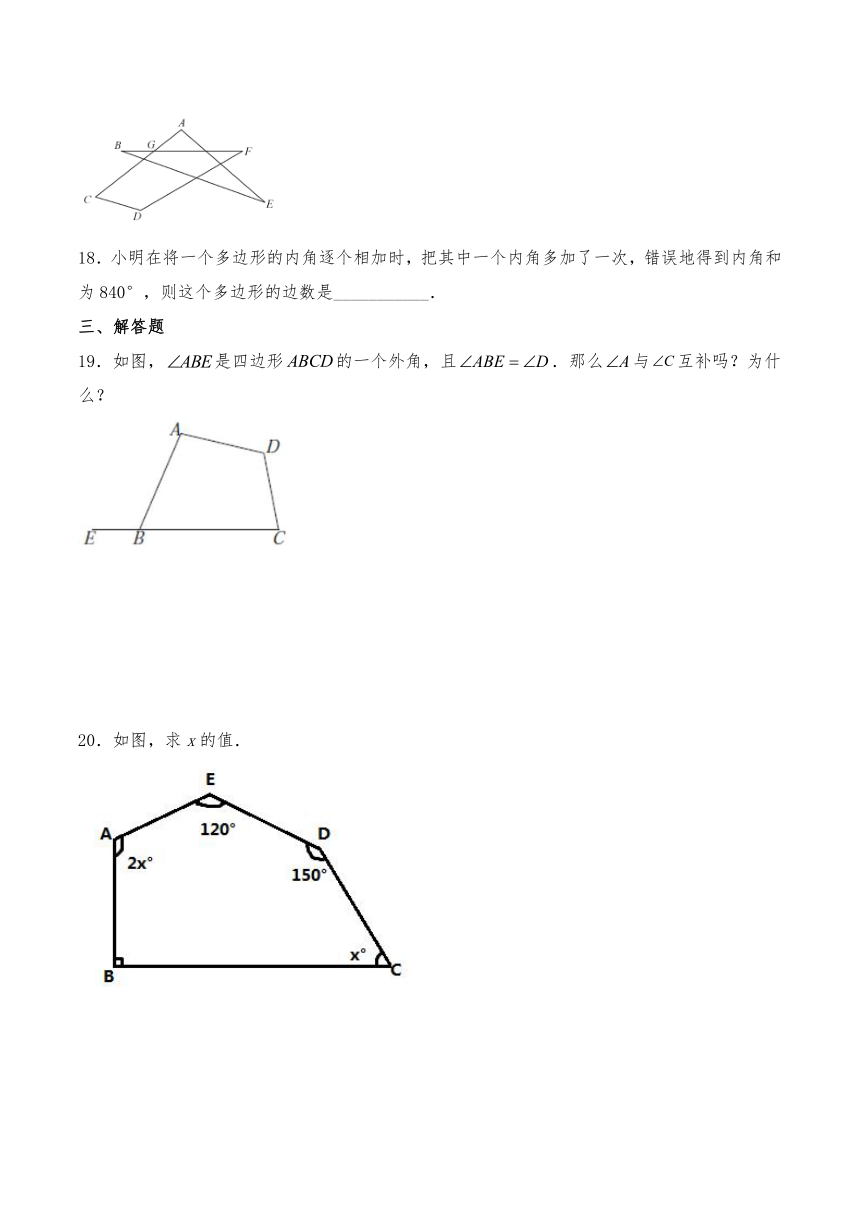
18.小明在将一个多边形的内角逐个相加时,把其中一个内角多加了一次,错误地得到内角和为840°,则这个多边形的边数是___________.
三、解答题
19.如图,是四边形的一个外角,且.那么与互补吗?为什么?
20.如图,求x的值.
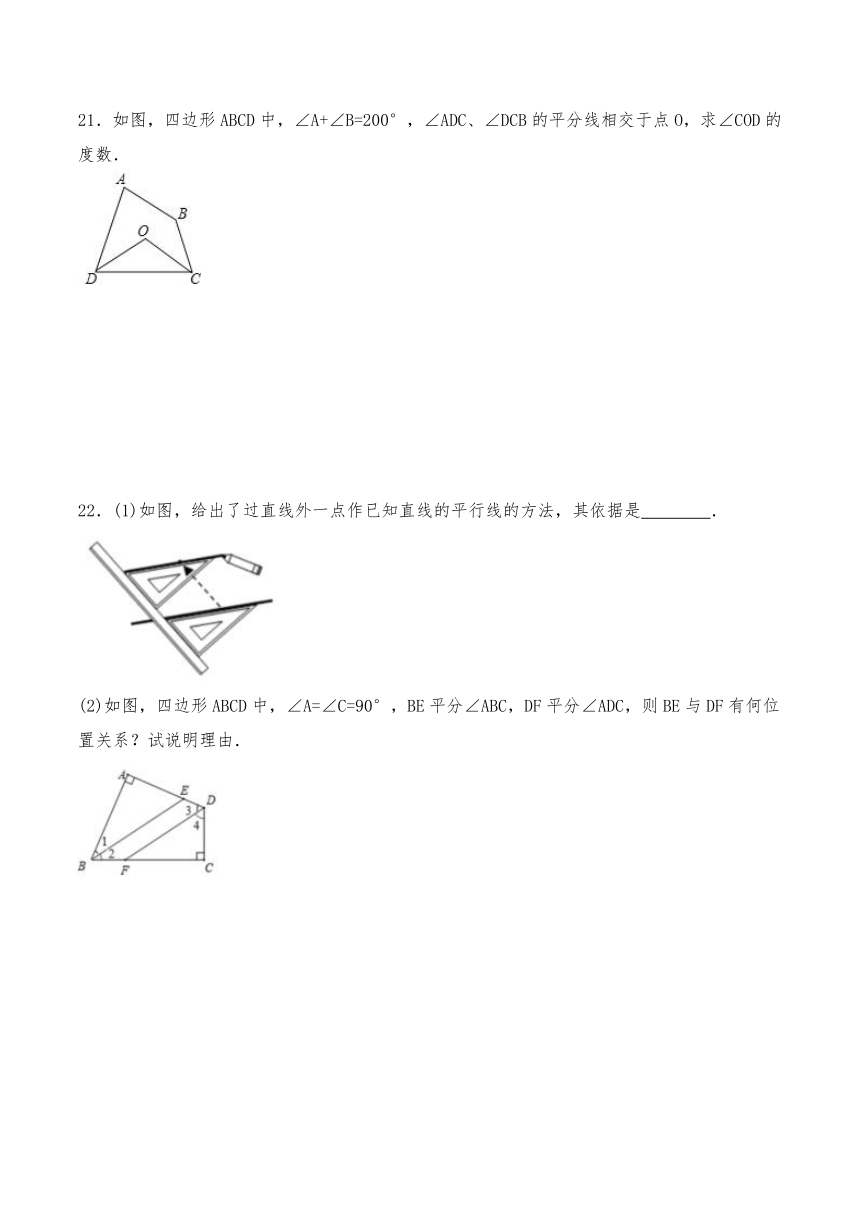
21.如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,求∠COD的度数.
22.(1)如图,给出了过直线外一点作已知直线的平行线的方法,其依据是
.
(2)如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.
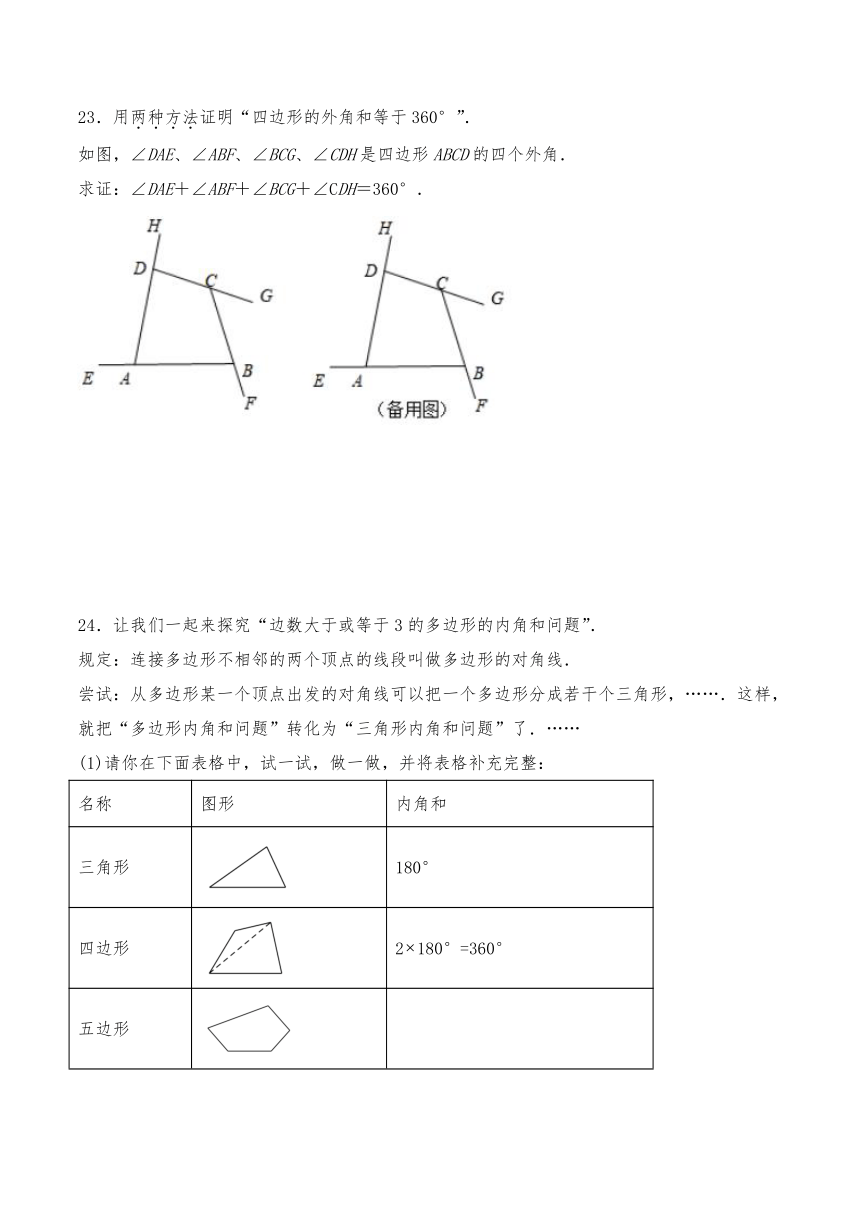
23.用两种方法证明“四边形的外角和等于360°”.
如图,∠DAE、∠ABF、∠BCG、∠CDH是四边形ABCD的四个外角.
求证:∠DAE+∠ABF+∠BCG+∠CDH=360°.
24.让我们一起来探究“边数大于或等于3的多边形的内角和问题”.
规定:连接多边形不相邻的两个顶点的线段叫做多边形的对角线.
尝试:从多边形某一个顶点出发的对角线可以把一个多边形分成若干个三角形,…….这样,就把“多边形内角和问题”转化为“三角形内角和问题”了.……
(1)请你在下面表格中,试一试,做一做,并将表格补充完整:
名称
图形
内角和
三角形
180°
四边形
2180°=360°
五边形
六边形
...
...
……
(2)根据上面的表格,请你猜一猜,七边形的内角和等于
;…….如果一个多边形有n条边,请你用含有n的代数式表示这个多边形的内角和
.
(3)如果一个多边形的内角和是1260°,请判断这个多边形是几边形.
25.如图1所示,称“对顶三角形”,其中,∠A+∠B=∠C+∠D
利用这个结论,完成下列填空.
(1)如图
(2),∠A+∠B+∠C+∠D+∠E=
;
(2)如图(3),∠A+∠B+∠C+∠D+∠E=
;
(3)如图(4),∠1+∠2+∠3+∠4+∠5+∠6=
;
(4)如图(5),∠1+∠2+∠3+∠4+∠5+∠6+∠7=
.
26.在中,,点,分别是边,上的点,点是一动点.记为,为,为.
(1)若点在线段上,且,如图1,则_____________;
(2)若点在边上运动,如图2所示,请猜想,,之间的关系,并说明理由;
(3)若点运动到边的延长线上,如图3所示,则,,之间又有何关系?请直接写出结论,不用说明理由.
答案
一、选择题
1.D.2.C.3.C.4.B.5.B.6.A.7.C.8.C.9.D.
10.C.11.D.12.B.13.C.14.C
二、填空题
15.8
16.5
17.360°
18.6.
三、解答题
19.与互补,理由如下:
∵,∠ABC+=180
∴∠ABC+∠D=180,
∵四边形内角和等于360,
∴+=360°-(∠ABC+∠D)=180°
∴与互补.
20.由已知可得
2x+120+150+x+90=(5-2)×180
解得x=60
21.解:∵四边形ABCD中,∠A+∠B=200°,
∴∠ADC+∠DCB=360°﹣200°=160°,
∵∠ADC、∠DCB的平分线相交于点O,
∴∠ODC=∠ADC,∠OCD=∠BCD,
∴∠ODC+∠OCD=×160°=80°,
∴∠COD=180°﹣80°=100°.
22.(1)图中给出了过直线外一点作已知直线的平行线的方法,其依据是:同位角相等,两直线平行
故答案为:同位角相等,两直线平行;
(2)BE∥DF.理由如下:
∵∠A=∠C=90°
∴∠ABC+∠ADC=360°-∠A-∠C
=180°
∵BE平分∠ABC,DF平分∠ADC,
∴∠1=∠2=∠ABC,∠3=∠4=∠ADC
∴∠1+∠3=(∠ABC+∠ADC)=×180°=90°
又∠1+∠AEB=90°
∴∠3=∠AEB
∴BE∥DF.
23.解:解法一:连接AC,BD,
∵∠EAD=∠ABD+∠ADB,
∠ABF=∠CAB+∠ACB,
∠BCG=∠CDB+∠CBD,
∠CDH=∠DAC+∠DCA,
∴∠DAE+∠ABF+∠BCG+∠CDH=∠ACB+∠ABC+∠CAB+∠ACB+∠CDB+∠CBD+∠DAC+∠DCA=(∠ACD+∠DCA+∠ADC)+(∠ABC+∠DAB+∠ACB)=180°+180°=360°.
解法二:
∵∠DAE+∠ABF+∠BCG+∠CDH=180°?∠DAB+180°?∠ABC+180°?∠BCD+180°?∠ADC,
又∵∠BAD+∠ABC+∠BCD+∠ADC=360°,
∴∠DAE+∠ABF+∠BCG+∠CDH=360°.
24.(1)表格如图所示:
图形
内角和
五边形
3180°=540°
六边形
4180°=720°
(2)七边形的内角和等于=5×180°900°;
n条边的内角和=(n-2)×180°.
故答案为900°,(n-2)180°.
(3)根据题意得(n-2)×180=1260,
解得:n=9.
答:这个多边形为九边形.
25.
解:如图:(1)∵∠1,∠2的和与∠D,∠E的和相等,
∴∠A+∠B+∠C+∠D+∠E=∠A+∠B+∠C+∠1+∠2=180°;
故答案为:180°;
(2)∵∠1,∠2的和与∠D,∠E的和相等,
∴∠A+∠B+∠C+∠D+∠E=∠A+∠B+∠C+∠1+∠2=180°;
故答案为:180°;
(3)∵∠1,∠2的和与∠7,∠8的和相等,
∴∠1+∠2+∠3+∠4+∠5+∠6=∠7+∠8+∠3+∠4+∠5+∠6=360°;
故答案为:360°;
(4)∵∠6,∠7的和与∠8,∠9的和相等,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+∠2+∠3+∠4+∠5+∠8+∠9=540°.
故答案为:540°
26.(1)∵∠1+∠PDC=180°,∠2+∠PEC=180°,
∴∠1+∠2+∠PDC+∠PEC=360°,
∵四边形CDPE的内角和是360°,
∴∠PDC+∠PEC+∠C+∠α=360°,
∴∠1+∠2=∠C+∠α=90°+50°=140°,
故答案为:140°;
(2)
理由:∵
∴
又∵四边形的内角和是
∴
∴
(3)由三角形的外角性质可知,∠3=∠2+∠α,
∴∠1=90°+∠3=90°+∠2+∠α.
《多边形及其内角和》习题1
一、选择题
1.七边形的内角和是( )
A.360°
B.540°
C.720°
D.900°
2.若一个正多边形的一个外角为45°,则这个正多边形的边数是(
)
A.6
B.7
C.8
D.9
3.如图,2×5的正方形网格中,用5张1×2的矩形纸片将网格完全覆盖,则不同的覆盖方法有(
)
A.3种
B.5种
C.8种
D.13种
4.若多边形的内角和大于
900°,则该多边形的边数最小为(
)
A.9
B.8
C.7
D.6
5.一个多边形的内角和是720°,这个多边形是( )
A.五边形
B.六边形
C.七边形
D.八边形
6.一个多边形的内角和比它的外角和的2倍还大180°,这个多边形的边数为( )
A.7
B.8
C.9
D.10
7.如果一个多边形的内角和是外角和的5倍,那么这个多边形的边数是( )
A.10
B.11
C.12
D.13
8.将一个圆形纸片,如下图连续对折三次之后,用剪刀剪去其方形部分,展开后得到的多边形的内角和角度为(
)
A.180°
B.540°
C.1080°
D.2160°
9.一个多边形的每个内角都相等,并且它的一个外角与一个内角的比为1:3,则这个多边形为(
)
A.三角形
B.四边形
C.六边形
D.八边形
10.下列多边形中,不能够单独铺满地面的是( )
A.正三角形
B.正方形
C.正五边形
D.正六边形
11.如图,是五边形的一个外角.若,则等于(
)
A.610?
B.470?
C.290?
D.430?
12.若一个多边形有27条对角线,则这个多边形的边数(
)
A.8
B.9
C.10
D.11
13.如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上(
)根木条.
A.
B.
C.
D.
14.如图,把边长相等的正六边形ABCDEF和正五边形ABGHI的AB边重合叠放在一起,连接EB,交HI于点K,则∠BKI的大小为( )
A.90°
B.85°
C.84°
D.80°
二、填空题
15.已知正n边形的一个外角是45°,则n=____________
16.若一个多边形的内角和与外角和之和是900°,则该多边形的边数是_____.
17.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数是_________________.
18.小明在将一个多边形的内角逐个相加时,把其中一个内角多加了一次,错误地得到内角和为840°,则这个多边形的边数是___________.
三、解答题
19.如图,是四边形的一个外角,且.那么与互补吗?为什么?
20.如图,求x的值.
21.如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,求∠COD的度数.
22.(1)如图,给出了过直线外一点作已知直线的平行线的方法,其依据是
.
(2)如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.
23.用两种方法证明“四边形的外角和等于360°”.
如图,∠DAE、∠ABF、∠BCG、∠CDH是四边形ABCD的四个外角.
求证:∠DAE+∠ABF+∠BCG+∠CDH=360°.
24.让我们一起来探究“边数大于或等于3的多边形的内角和问题”.
规定:连接多边形不相邻的两个顶点的线段叫做多边形的对角线.
尝试:从多边形某一个顶点出发的对角线可以把一个多边形分成若干个三角形,…….这样,就把“多边形内角和问题”转化为“三角形内角和问题”了.……
(1)请你在下面表格中,试一试,做一做,并将表格补充完整:
名称
图形
内角和
三角形
180°
四边形
2180°=360°
五边形
六边形
...
...
……
(2)根据上面的表格,请你猜一猜,七边形的内角和等于
;…….如果一个多边形有n条边,请你用含有n的代数式表示这个多边形的内角和
.
(3)如果一个多边形的内角和是1260°,请判断这个多边形是几边形.
25.如图1所示,称“对顶三角形”,其中,∠A+∠B=∠C+∠D
利用这个结论,完成下列填空.
(1)如图
(2),∠A+∠B+∠C+∠D+∠E=
;
(2)如图(3),∠A+∠B+∠C+∠D+∠E=
;
(3)如图(4),∠1+∠2+∠3+∠4+∠5+∠6=
;
(4)如图(5),∠1+∠2+∠3+∠4+∠5+∠6+∠7=
.
26.在中,,点,分别是边,上的点,点是一动点.记为,为,为.
(1)若点在线段上,且,如图1,则_____________;
(2)若点在边上运动,如图2所示,请猜想,,之间的关系,并说明理由;
(3)若点运动到边的延长线上,如图3所示,则,,之间又有何关系?请直接写出结论,不用说明理由.
答案
一、选择题
1.D.2.C.3.C.4.B.5.B.6.A.7.C.8.C.9.D.
10.C.11.D.12.B.13.C.14.C
二、填空题
15.8
16.5
17.360°
18.6.
三、解答题
19.与互补,理由如下:
∵,∠ABC+=180
∴∠ABC+∠D=180,
∵四边形内角和等于360,
∴+=360°-(∠ABC+∠D)=180°
∴与互补.
20.由已知可得
2x+120+150+x+90=(5-2)×180
解得x=60
21.解:∵四边形ABCD中,∠A+∠B=200°,
∴∠ADC+∠DCB=360°﹣200°=160°,
∵∠ADC、∠DCB的平分线相交于点O,
∴∠ODC=∠ADC,∠OCD=∠BCD,
∴∠ODC+∠OCD=×160°=80°,
∴∠COD=180°﹣80°=100°.
22.(1)图中给出了过直线外一点作已知直线的平行线的方法,其依据是:同位角相等,两直线平行
故答案为:同位角相等,两直线平行;
(2)BE∥DF.理由如下:
∵∠A=∠C=90°
∴∠ABC+∠ADC=360°-∠A-∠C
=180°
∵BE平分∠ABC,DF平分∠ADC,
∴∠1=∠2=∠ABC,∠3=∠4=∠ADC
∴∠1+∠3=(∠ABC+∠ADC)=×180°=90°
又∠1+∠AEB=90°
∴∠3=∠AEB
∴BE∥DF.
23.解:解法一:连接AC,BD,
∵∠EAD=∠ABD+∠ADB,
∠ABF=∠CAB+∠ACB,
∠BCG=∠CDB+∠CBD,
∠CDH=∠DAC+∠DCA,
∴∠DAE+∠ABF+∠BCG+∠CDH=∠ACB+∠ABC+∠CAB+∠ACB+∠CDB+∠CBD+∠DAC+∠DCA=(∠ACD+∠DCA+∠ADC)+(∠ABC+∠DAB+∠ACB)=180°+180°=360°.
解法二:
∵∠DAE+∠ABF+∠BCG+∠CDH=180°?∠DAB+180°?∠ABC+180°?∠BCD+180°?∠ADC,
又∵∠BAD+∠ABC+∠BCD+∠ADC=360°,
∴∠DAE+∠ABF+∠BCG+∠CDH=360°.
24.(1)表格如图所示:
图形
内角和
五边形
3180°=540°
六边形
4180°=720°
(2)七边形的内角和等于=5×180°900°;
n条边的内角和=(n-2)×180°.
故答案为900°,(n-2)180°.
(3)根据题意得(n-2)×180=1260,
解得:n=9.
答:这个多边形为九边形.
25.
解:如图:(1)∵∠1,∠2的和与∠D,∠E的和相等,
∴∠A+∠B+∠C+∠D+∠E=∠A+∠B+∠C+∠1+∠2=180°;
故答案为:180°;
(2)∵∠1,∠2的和与∠D,∠E的和相等,
∴∠A+∠B+∠C+∠D+∠E=∠A+∠B+∠C+∠1+∠2=180°;
故答案为:180°;
(3)∵∠1,∠2的和与∠7,∠8的和相等,
∴∠1+∠2+∠3+∠4+∠5+∠6=∠7+∠8+∠3+∠4+∠5+∠6=360°;
故答案为:360°;
(4)∵∠6,∠7的和与∠8,∠9的和相等,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+∠2+∠3+∠4+∠5+∠8+∠9=540°.
故答案为:540°
26.(1)∵∠1+∠PDC=180°,∠2+∠PEC=180°,
∴∠1+∠2+∠PDC+∠PEC=360°,
∵四边形CDPE的内角和是360°,
∴∠PDC+∠PEC+∠C+∠α=360°,
∴∠1+∠2=∠C+∠α=90°+50°=140°,
故答案为:140°;
(2)
理由:∵
∴
又∵四边形的内角和是
∴
∴
(3)由三角形的外角性质可知,∠3=∠2+∠α,
∴∠1=90°+∠3=90°+∠2+∠α.
