八年级数学上册试题 一课一练12.3 《角的平分线的性质》习题1-人教版(word版含答案)
文档属性
| 名称 | 八年级数学上册试题 一课一练12.3 《角的平分线的性质》习题1-人教版(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 522.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 15:39:08 | ||
图片预览


文档简介
12.3
《角的平分线的性质》习题1
一、选择题
1.工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的到刻度分别与点M、N重合,过角尺顶点C作射线OC由此作法便可得△NOC≌△MOC,其依据是( )
A.SSS
B.SAS
C.ASA
D.AAS
2.如图,Rt△ABC中,∠C=90°,用尺规作图法作出射线AE,AE交BC于点D,CD=2,P为AB上一动点,则PD的最小值为( )
A.2
B.3
C.4
D.无法确定
3.已知△ABC,两个完全一样的三角板如图摆放,它们的一组对应直角边分别在AB,AC上,且这组对应边所对的顶点重合于点M,点M一定在(
).
A.∠A的平分线上
B.AC边的高上
C.BC边的垂直平分线上
D.AB边的中线上
4.如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于EF长为半径作圆弧,两条圆弧交于点P,连接AP,交CD于点M,若∠ACD=110°,则∠CMA的度数为( )
A.30°
B.35°
C.70°
D.45°
5.如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于(
)
A.1:1:1
B.1:2:3
C.2:3:4
D.3:4:5
6.到△ABC的三条边距离相等的点是△ABC的(
).
A.三条中线的交点
B.三条边的垂直平分线的交点
C.三条高的交点
D.三条角平分线的交点
7.如图,三条公路两两相交,现计划修建一个油库,要求油库到这三条公路的距离相等,那么选择油库的位置有(
)处.
A.1
B.2
C.3
D.4
8.如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为(
)
A.a=b
B.2a+b=﹣1
C.2a﹣b=1
D.2a+b=1
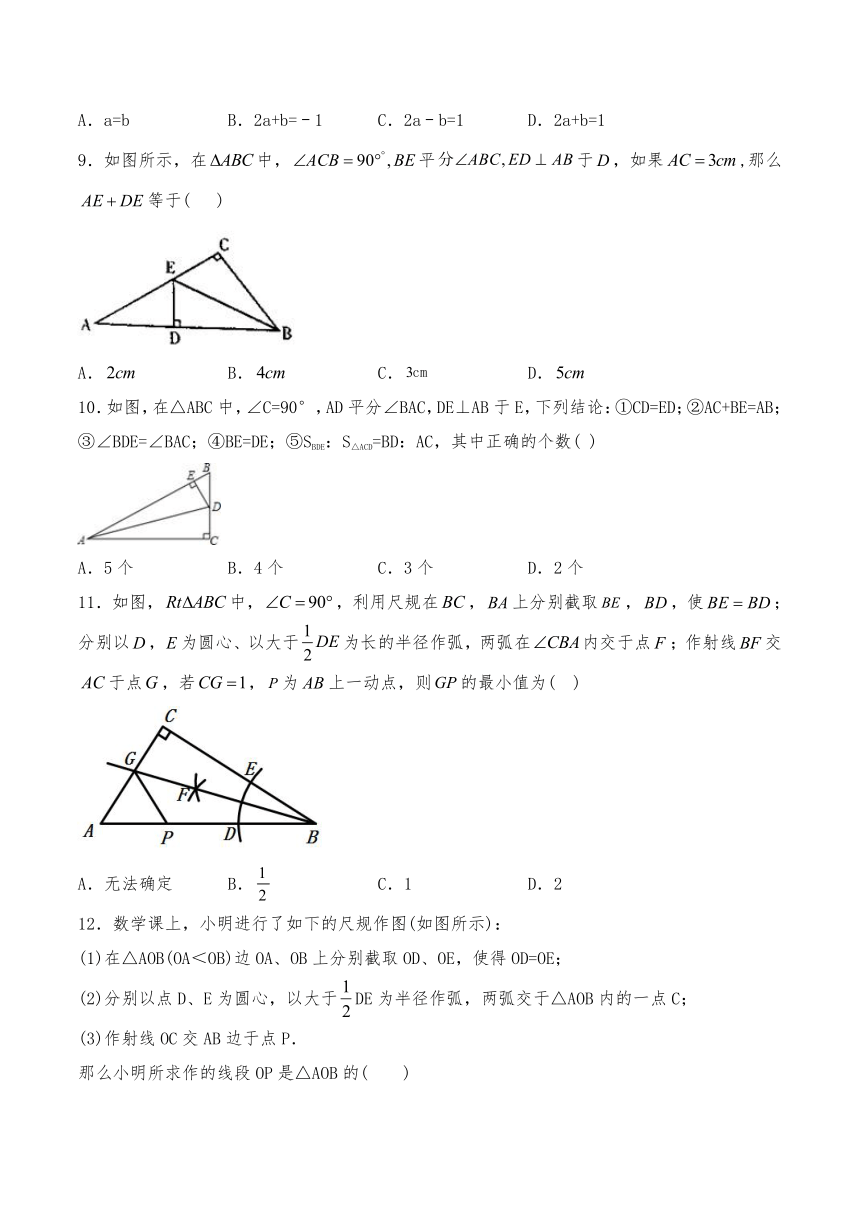
9.如图所示,在中,平于,如果,那么等于(
)
A.
B.
C.
D.
10.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④BE=DE;⑤SBDE:S△ACD=BD:AC,其中正确的个数(
)
A.5个
B.4个
C.3个
D.2个
11.如图,中,,利用尺规在,上分别截取,,使;分别以,为圆心、以大于为长的半径作弧,两弧在内交于点;作射线交于点,若,为上一动点,则的最小值为(
)
A.无法确定
B.
C.1
D.2
12.数学课上,小明进行了如下的尺规作图(如图所示):
(1)在△AOB(OA<OB)边OA、OB上分别截取OD、OE,使得OD=OE;
(2)分别以点D、E为圆心,以大于DE为半径作弧,两弧交于△AOB内的一点C;
(3)作射线OC交AB边于点P.
那么小明所求作的线段OP是△AOB的( )
A.一条中线
B.一条高
C.一条角平分线
D.不确定
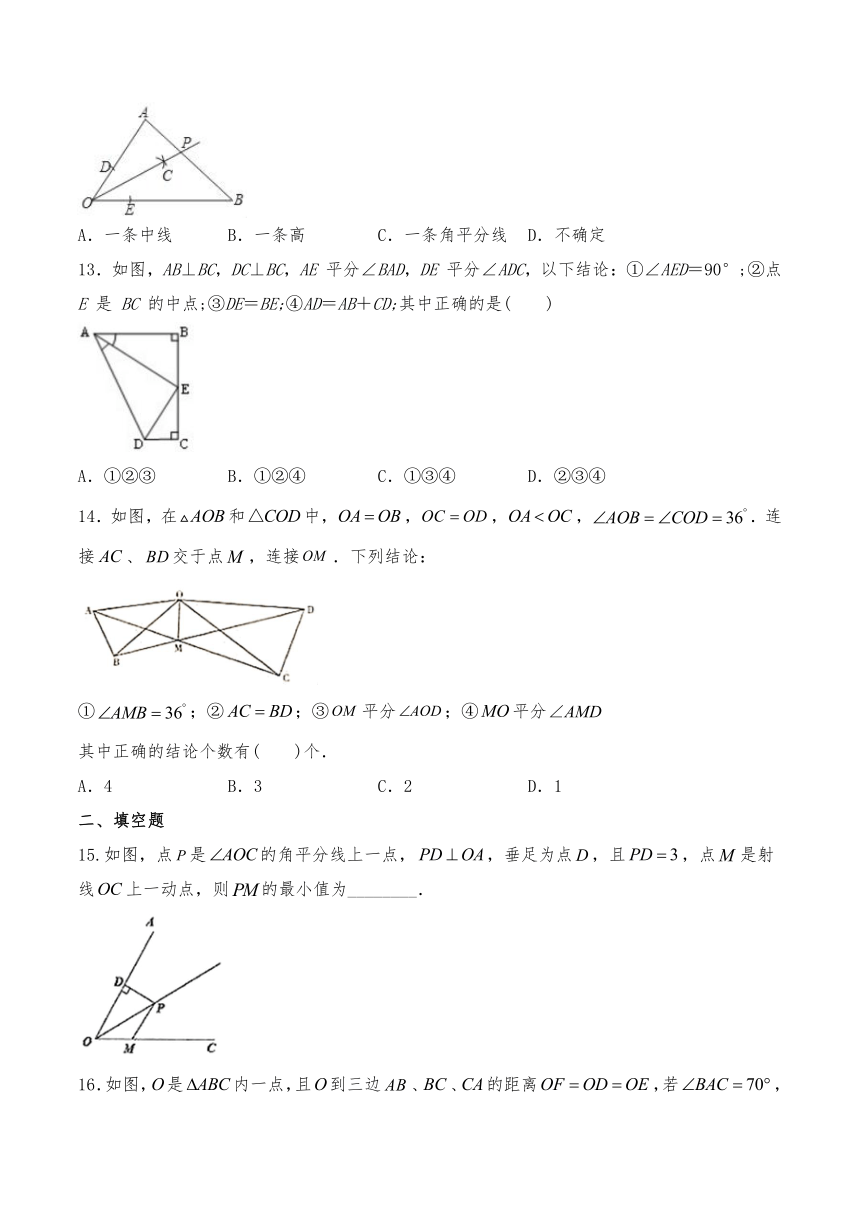
13.如图,AB⊥BC,DC⊥BC,AE
平分∠BAD,DE
平分∠ADC,以下结论:①∠AED=90°;②点
E
是
BC
的中点;③DE=BE;④AD=AB+CD;其中正确的是(
)
A.①②③
B.①②④
C.①③④
D.②③④
14.如图,在和中,,,,.连接、交于点,连接.下列结论:
①;②;③平分;④平分
其中正确的结论个数有(
)个.
A.4
B.3
C.2
D.1
二、填空题
15.如图,点是的角平分线上一点,,垂足为点,且,点是射线上一动点,则的最小值为________.
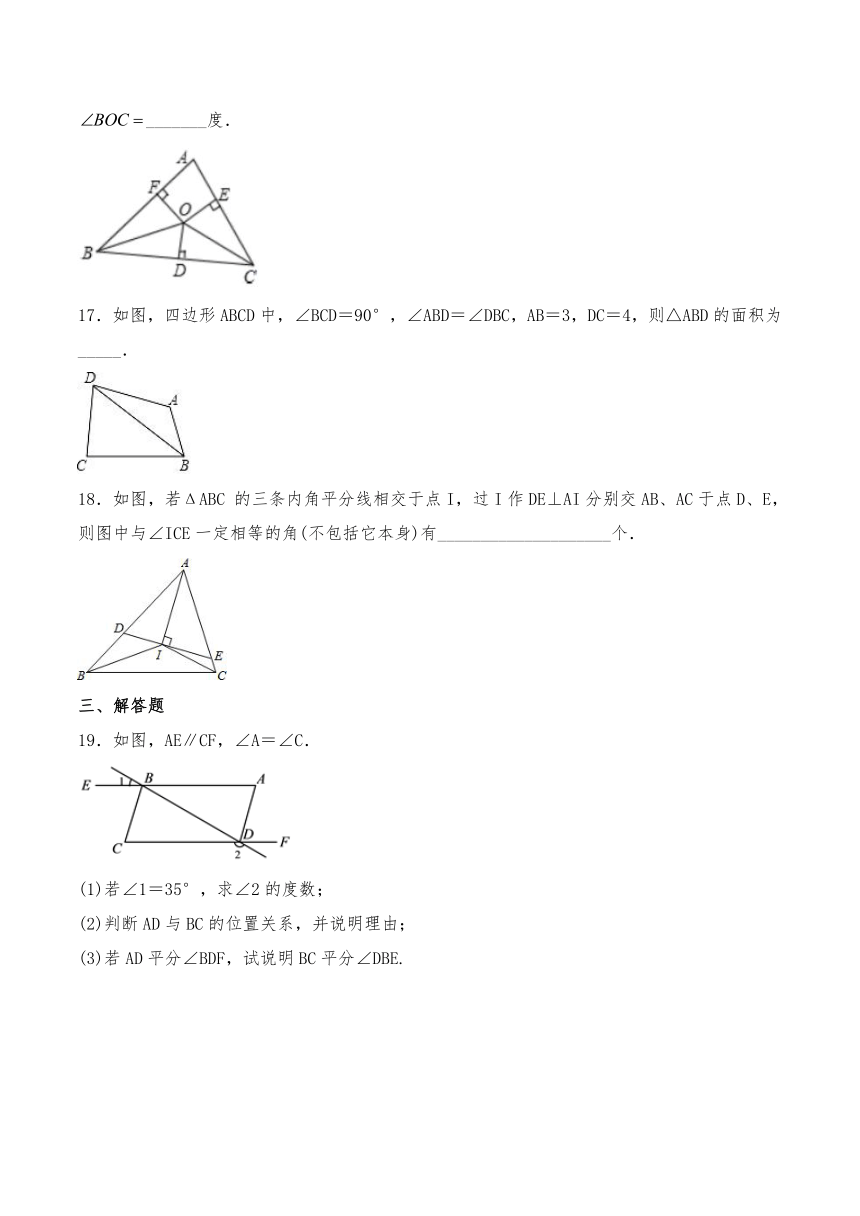
16.如图,是内一点,且到三边、、的距离,若,_______度.
17.如图,四边形ABCD中,∠BCD=90°,∠ABD=∠DBC,AB=3,DC=4,则△ABD的面积为_____.
18.如图,若ΔABC
的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E,则图中与∠ICE一定相等的角(不包括它本身)有____________________个.
三、解答题
19.如图,AE∥CF,∠A=∠C.
(1)若∠1=35°,求∠2的度数;
(2)判断AD与BC的位置关系,并说明理由;
(3)若AD平分∠BDF,试说明BC平分∠DBE.
20.如图,在每个小正方形的边长为1的网格中,A,B,C均为格点.
(1)的面积等于;
(2)请用无刻度的直尺,在如图所示的网格中画出的角平分线BD,并在AB边上画出点P,使得,并简要说明的角平分线BD及点P的位置是如何找到的(不要求证明)
21.下面是小明设计的“在已知三角形的一边上取一点,使得这点到这个三角形的另外两边的距离相等”的尺规作图过程:
已知:△ABC.
求作:点D,使得点D在BC边上,且到AB,AC边的距离相等.
作法:如图,
作∠BAC的平分线,交BC于点D.则点D即为所求.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形
(保留作图痕迹);
(2)完成下面的证明.
证明:作DE⊥AB于点E,作DF⊥AC于点F,
∵AD平分∠BAC,
∴
=
(
)
(填推理的依据)
.
22.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)试判断AB与AF,EB之间存在的数量关系,并说明理由.
23.如图所示点在上且.
求证:.
若,求证:平分.
24.如图,在ABC中,∠C=90?,BD是ABC的一条角一平分线,点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形,
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长
25.如图,已知∠AOB,以O为圆心,以任意长为半径作弧,分别交OA,OB于F,E两点,再分别以E,F为圆心,大于EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D.
(1)若∠OFD=116°,求∠DOB的度数;
(2)若FM⊥OD,垂足为M,求证:△FMO≌△FMD.
26.已知(如图1)在△ABC中,∠B>∠C,AD平分∠BAC,点E在AD的延长线上,过点E作EF⊥BC于点F,设∠B=α,∠C=β.
(1)当α=80°,β=30°时,求∠E的度数;
(2)试问∠E与∠B,∠C之间存在着怎样的数量关系,试用α、β表示∠E,并说明理由;
(3)若∠EFB与∠BAE平分线交于点P(如图2),当点E在AD延长线上运动时,∠P是否发生变化,若不变,请用α、β表示∠P;若变化,请说明理由.
答案
一、选择题
1.A.2.A.3.C.4.B.5.C.6.D7.D.8.B.9.C.
10.C.11.C.12.C.13.B.14.B.
二、填空题
15.3
16.125
17.6
18.2
三、解答题
19.(1)∵AE∥CF,
∴∠BDC=∠1=35°,
又∵∠2+∠BDC=180°,
∴∠2=180°-∠BDC=180°-35°=145°;
(2)BC∥AD.
理由:∵AE∥CF,∴∠A+∠ADC=180°,
又∵∠A=∠C,∴∠C+∠ADC=180°,
∴BC∥AD.
(3)∵AE∥CF,∴∠BDF=∠DBE.
∵BC∥AD,∴∠ADB=∠DBC.
∵AD平分∠BDF,∴∠ADB=∠BDF,∴∠DBC=∠EBD.
∴BC平分∠DBE.
20.解:(1);
(2)如图,取格点M,N,连接MN,MN与网格线交于点D,连接BD即为所求;BD与网格线交于点E,取格点G,H,GH与网格线交于点F,过点E,F画直线,直线EF
交AB于点P即为所求.
21.解:(1)作∠BAC的角平分线,如图:
(2)作DE⊥AB于点E,作DF⊥AC于点F,
∵AD平分∠BAC,
∴DE=DF(角平分线上的点到角两边的距离相等).
故答案为:DE,DF,角平分线上的点到角两边的距离相等.
22.(1)证明:∵AD是∠BAC的平分线,DE⊥AB,∠C=90,
∴DC=DE,
在Rt△FCD和Rt△BED中,
,
∴Rt△FCD≌Rt△BED,
∴CF=EB;
(2)解:在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED,
∴AC=AE,
∴AB=AE+BE=AF+FC+BE=AF+2BE.
23.
证明:(1)∵
∴
即
∵
∴在和中
∴
∴
(2)∵
∴
∵
∴
在和中
∴
∴
∴平分.
24.解:(1)过点O作OM⊥AB于点M
∵正方形OECF
∴OE=EC=CF=OF,OE⊥BC于E,OF⊥AC于F
∵BD平分∠ABC,OM⊥AB于M,OE⊥BC于E
∴OM=OE=OF
∵OM⊥AB于M,
OE⊥BC于E
∴∠AMO=90°,∠AFO=90°
∵
∴Rt△AMO≌Rt△AFO
∴∠MA0=∠FAO
∴点O在∠BAC的平分线上
(2)∵Rt△ABC中,∠C=90°,AC=5,BC=12
∴AB=13
∴BE=BM,AM=AF
又BE=BC-CE,AF=AC-CF,而CE=CF=OE
∴BE=12-OE,AF=5-OE
∴BM+AM=AB
即BE+AF=13
12-OE+5-OE=13
解得OE=2
25.(1)∵OB∥FD,
∴∠OFD+∠AOB=18O°,
又∵∠OFD=116°,
∴∠AOB=180°﹣∠OFD=180°﹣116°=64°,
由作法知,OP是∠AOB的平分线,
∴∠DOB=∠AOB=32°;
(2)证明:∵OP平分∠AOB,
∴∠AOD=∠DOB,
∵OB∥FD,
∴∠DOB=∠ODF,
∴∠AOD=∠ODF,
又∵FM⊥OD,
∴∠OMF=∠DMF,
在△MFO和△MFD中
,
∴△MFO≌△MFD(AAS).
26.(1)∵EF⊥BC,
∴∠E=90°?∠EDF,
∵AD平分∠BAC,
∴∠EDF=∠C+∠CAB,
又∵∠CAB=180°?∠B?∠C=70°,
∴∠EDF=30°+35°=65°,
∴∠E=90°?65°=25°;
(2)∵EF⊥BC,
∴∠E=90°?∠EDF,
∵AD平分∠BAC,
∴∠EDF=β+∠CAB,
又∵∠CAB=180°?α?β,
∴∠EDF=β+90°?=90°+,
∴∠E=90°?90°=,
即∠E
=;
(3)∠P度数不会发生变化,证明如下:
如图,设AP与BC交于M点,
∵FP平分∠EFB,EF⊥BC,
∴∠PFB=45°,
∵AP平分∠BAE,AD平分∠BAC,
∴∠BAP=∠BAD=∠BAC=∠BAC,
∵∠BAC=180°?α?β,
∴∠BAP=45°α?β,
∴∠PMF=∠AMB=180°?45°+α+β?α=135°+β?α,
∴∠P=180°?∠PFB?∠PMF=180°?45°?135°β+α=αβ,
即∠P=αβ.
《角的平分线的性质》习题1
一、选择题
1.工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的到刻度分别与点M、N重合,过角尺顶点C作射线OC由此作法便可得△NOC≌△MOC,其依据是( )
A.SSS
B.SAS
C.ASA
D.AAS
2.如图,Rt△ABC中,∠C=90°,用尺规作图法作出射线AE,AE交BC于点D,CD=2,P为AB上一动点,则PD的最小值为( )
A.2
B.3
C.4
D.无法确定
3.已知△ABC,两个完全一样的三角板如图摆放,它们的一组对应直角边分别在AB,AC上,且这组对应边所对的顶点重合于点M,点M一定在(
).
A.∠A的平分线上
B.AC边的高上
C.BC边的垂直平分线上
D.AB边的中线上
4.如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于EF长为半径作圆弧,两条圆弧交于点P,连接AP,交CD于点M,若∠ACD=110°,则∠CMA的度数为( )
A.30°
B.35°
C.70°
D.45°
5.如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于(
)
A.1:1:1
B.1:2:3
C.2:3:4
D.3:4:5
6.到△ABC的三条边距离相等的点是△ABC的(
).
A.三条中线的交点
B.三条边的垂直平分线的交点
C.三条高的交点
D.三条角平分线的交点
7.如图,三条公路两两相交,现计划修建一个油库,要求油库到这三条公路的距离相等,那么选择油库的位置有(
)处.
A.1
B.2
C.3
D.4
8.如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为(
)
A.a=b
B.2a+b=﹣1
C.2a﹣b=1
D.2a+b=1
9.如图所示,在中,平于,如果,那么等于(
)
A.
B.
C.
D.
10.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④BE=DE;⑤SBDE:S△ACD=BD:AC,其中正确的个数(
)
A.5个
B.4个
C.3个
D.2个
11.如图,中,,利用尺规在,上分别截取,,使;分别以,为圆心、以大于为长的半径作弧,两弧在内交于点;作射线交于点,若,为上一动点,则的最小值为(
)
A.无法确定
B.
C.1
D.2
12.数学课上,小明进行了如下的尺规作图(如图所示):
(1)在△AOB(OA<OB)边OA、OB上分别截取OD、OE,使得OD=OE;
(2)分别以点D、E为圆心,以大于DE为半径作弧,两弧交于△AOB内的一点C;
(3)作射线OC交AB边于点P.
那么小明所求作的线段OP是△AOB的( )
A.一条中线
B.一条高
C.一条角平分线
D.不确定
13.如图,AB⊥BC,DC⊥BC,AE
平分∠BAD,DE
平分∠ADC,以下结论:①∠AED=90°;②点
E
是
BC
的中点;③DE=BE;④AD=AB+CD;其中正确的是(
)
A.①②③
B.①②④
C.①③④
D.②③④
14.如图,在和中,,,,.连接、交于点,连接.下列结论:
①;②;③平分;④平分
其中正确的结论个数有(
)个.
A.4
B.3
C.2
D.1
二、填空题
15.如图,点是的角平分线上一点,,垂足为点,且,点是射线上一动点,则的最小值为________.
16.如图,是内一点,且到三边、、的距离,若,_______度.
17.如图,四边形ABCD中,∠BCD=90°,∠ABD=∠DBC,AB=3,DC=4,则△ABD的面积为_____.
18.如图,若ΔABC
的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E,则图中与∠ICE一定相等的角(不包括它本身)有____________________个.
三、解答题
19.如图,AE∥CF,∠A=∠C.
(1)若∠1=35°,求∠2的度数;
(2)判断AD与BC的位置关系,并说明理由;
(3)若AD平分∠BDF,试说明BC平分∠DBE.
20.如图,在每个小正方形的边长为1的网格中,A,B,C均为格点.
(1)的面积等于;
(2)请用无刻度的直尺,在如图所示的网格中画出的角平分线BD,并在AB边上画出点P,使得,并简要说明的角平分线BD及点P的位置是如何找到的(不要求证明)
21.下面是小明设计的“在已知三角形的一边上取一点,使得这点到这个三角形的另外两边的距离相等”的尺规作图过程:
已知:△ABC.
求作:点D,使得点D在BC边上,且到AB,AC边的距离相等.
作法:如图,
作∠BAC的平分线,交BC于点D.则点D即为所求.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形
(保留作图痕迹);
(2)完成下面的证明.
证明:作DE⊥AB于点E,作DF⊥AC于点F,
∵AD平分∠BAC,
∴
=
(
)
(填推理的依据)
.
22.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)试判断AB与AF,EB之间存在的数量关系,并说明理由.
23.如图所示点在上且.
求证:.
若,求证:平分.
24.如图,在ABC中,∠C=90?,BD是ABC的一条角一平分线,点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形,
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长
25.如图,已知∠AOB,以O为圆心,以任意长为半径作弧,分别交OA,OB于F,E两点,再分别以E,F为圆心,大于EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D.
(1)若∠OFD=116°,求∠DOB的度数;
(2)若FM⊥OD,垂足为M,求证:△FMO≌△FMD.
26.已知(如图1)在△ABC中,∠B>∠C,AD平分∠BAC,点E在AD的延长线上,过点E作EF⊥BC于点F,设∠B=α,∠C=β.
(1)当α=80°,β=30°时,求∠E的度数;
(2)试问∠E与∠B,∠C之间存在着怎样的数量关系,试用α、β表示∠E,并说明理由;
(3)若∠EFB与∠BAE平分线交于点P(如图2),当点E在AD延长线上运动时,∠P是否发生变化,若不变,请用α、β表示∠P;若变化,请说明理由.
答案
一、选择题
1.A.2.A.3.C.4.B.5.C.6.D7.D.8.B.9.C.
10.C.11.C.12.C.13.B.14.B.
二、填空题
15.3
16.125
17.6
18.2
三、解答题
19.(1)∵AE∥CF,
∴∠BDC=∠1=35°,
又∵∠2+∠BDC=180°,
∴∠2=180°-∠BDC=180°-35°=145°;
(2)BC∥AD.
理由:∵AE∥CF,∴∠A+∠ADC=180°,
又∵∠A=∠C,∴∠C+∠ADC=180°,
∴BC∥AD.
(3)∵AE∥CF,∴∠BDF=∠DBE.
∵BC∥AD,∴∠ADB=∠DBC.
∵AD平分∠BDF,∴∠ADB=∠BDF,∴∠DBC=∠EBD.
∴BC平分∠DBE.
20.解:(1);
(2)如图,取格点M,N,连接MN,MN与网格线交于点D,连接BD即为所求;BD与网格线交于点E,取格点G,H,GH与网格线交于点F,过点E,F画直线,直线EF
交AB于点P即为所求.
21.解:(1)作∠BAC的角平分线,如图:
(2)作DE⊥AB于点E,作DF⊥AC于点F,
∵AD平分∠BAC,
∴DE=DF(角平分线上的点到角两边的距离相等).
故答案为:DE,DF,角平分线上的点到角两边的距离相等.
22.(1)证明:∵AD是∠BAC的平分线,DE⊥AB,∠C=90,
∴DC=DE,
在Rt△FCD和Rt△BED中,
,
∴Rt△FCD≌Rt△BED,
∴CF=EB;
(2)解:在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED,
∴AC=AE,
∴AB=AE+BE=AF+FC+BE=AF+2BE.
23.
证明:(1)∵
∴
即
∵
∴在和中
∴
∴
(2)∵
∴
∵
∴
在和中
∴
∴
∴平分.
24.解:(1)过点O作OM⊥AB于点M
∵正方形OECF
∴OE=EC=CF=OF,OE⊥BC于E,OF⊥AC于F
∵BD平分∠ABC,OM⊥AB于M,OE⊥BC于E
∴OM=OE=OF
∵OM⊥AB于M,
OE⊥BC于E
∴∠AMO=90°,∠AFO=90°
∵
∴Rt△AMO≌Rt△AFO
∴∠MA0=∠FAO
∴点O在∠BAC的平分线上
(2)∵Rt△ABC中,∠C=90°,AC=5,BC=12
∴AB=13
∴BE=BM,AM=AF
又BE=BC-CE,AF=AC-CF,而CE=CF=OE
∴BE=12-OE,AF=5-OE
∴BM+AM=AB
即BE+AF=13
12-OE+5-OE=13
解得OE=2
25.(1)∵OB∥FD,
∴∠OFD+∠AOB=18O°,
又∵∠OFD=116°,
∴∠AOB=180°﹣∠OFD=180°﹣116°=64°,
由作法知,OP是∠AOB的平分线,
∴∠DOB=∠AOB=32°;
(2)证明:∵OP平分∠AOB,
∴∠AOD=∠DOB,
∵OB∥FD,
∴∠DOB=∠ODF,
∴∠AOD=∠ODF,
又∵FM⊥OD,
∴∠OMF=∠DMF,
在△MFO和△MFD中
,
∴△MFO≌△MFD(AAS).
26.(1)∵EF⊥BC,
∴∠E=90°?∠EDF,
∵AD平分∠BAC,
∴∠EDF=∠C+∠CAB,
又∵∠CAB=180°?∠B?∠C=70°,
∴∠EDF=30°+35°=65°,
∴∠E=90°?65°=25°;
(2)∵EF⊥BC,
∴∠E=90°?∠EDF,
∵AD平分∠BAC,
∴∠EDF=β+∠CAB,
又∵∠CAB=180°?α?β,
∴∠EDF=β+90°?=90°+,
∴∠E=90°?90°=,
即∠E
=;
(3)∠P度数不会发生变化,证明如下:
如图,设AP与BC交于M点,
∵FP平分∠EFB,EF⊥BC,
∴∠PFB=45°,
∵AP平分∠BAE,AD平分∠BAC,
∴∠BAP=∠BAD=∠BAC=∠BAC,
∵∠BAC=180°?α?β,
∴∠BAP=45°α?β,
∴∠PMF=∠AMB=180°?45°+α+β?α=135°+β?α,
∴∠P=180°?∠PFB?∠PMF=180°?45°?135°β+α=αβ,
即∠P=αβ.
