11.2.1 第1课时 三角形的内角和—人教版八年级数学上册课时作业(含答案)
文档属性
| 名称 | 11.2.1 第1课时 三角形的内角和—人教版八年级数学上册课时作业(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 401.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 16:05:57 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版八年级数学上册课时作业
第十一章 三角形
11.2 与三角形有关的角
11.2.1 三角形的内角
第1课时 三角形的内角和
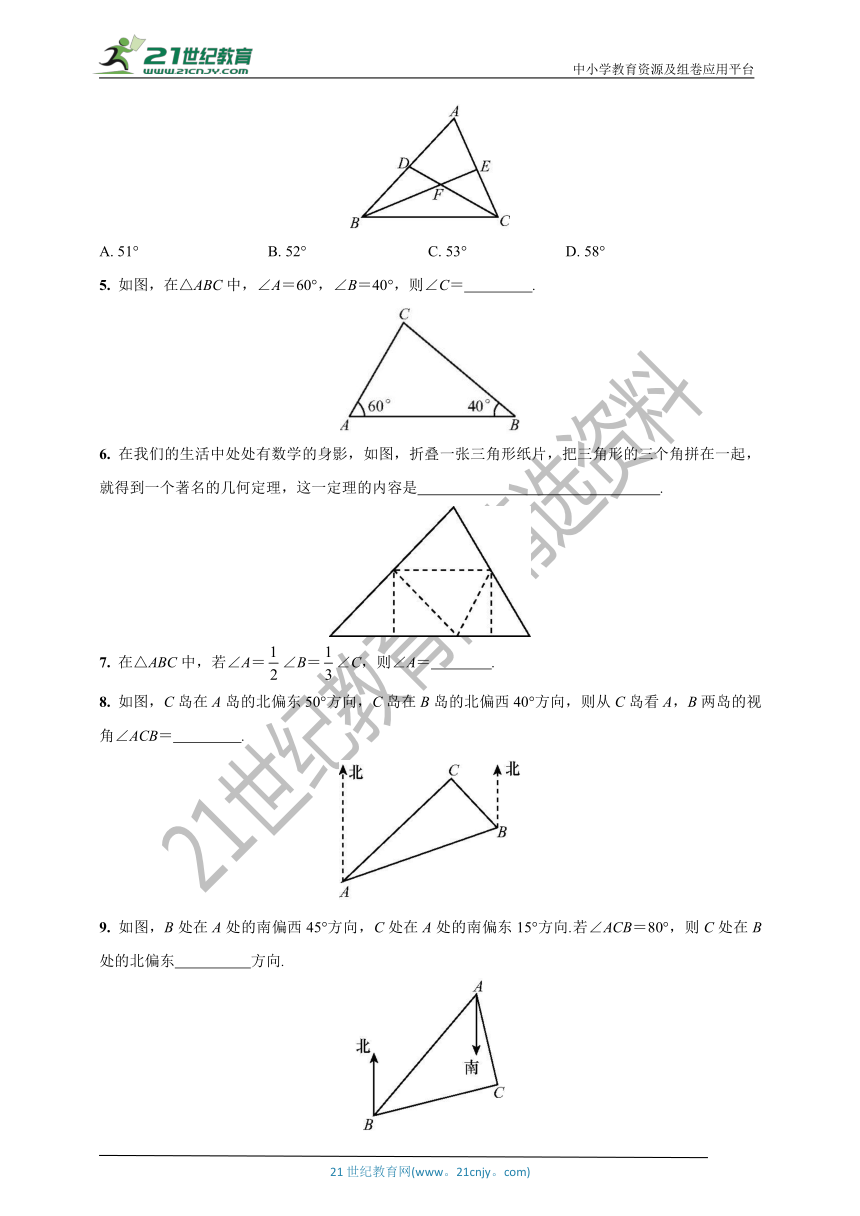
1. 如图是一块三角形木板的残余部分,量得∠A=110°,∠B=30°,则这块三角形木板缺少的角的度数是( )
A. 30° B. 40° C. 50° D. 60°
2. 如图,小明将文具盒里的一副三角板叠放在一起,则图中的∠α等于( )
A. 105° B. 115° C. 125° D. 135°
3. 如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于点E,∠BAC=60°,∠ABE=25°,则∠DAC的大小是( )
A. 15° B. 20° C. 25° D. 30°
4. 如图,在△ABC中,∠B,∠C的平分线BE,CD相交于点F.若∠BFC=116°,则∠A等于( )
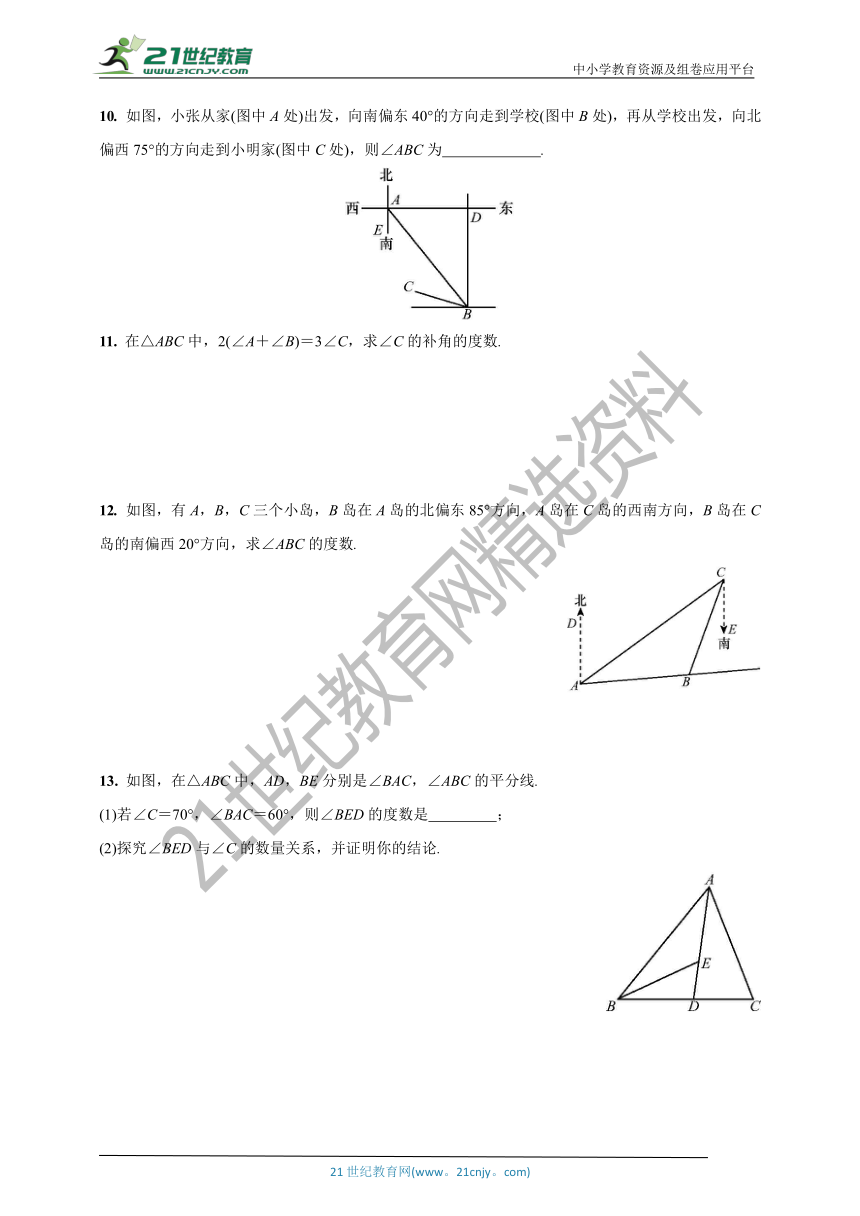
A. 51° B. 52° C. 53° D. 58°
5. 如图,在△ABC中,∠A=60°,∠B=40°,则∠C= .?
6. 在我们的生活中处处有数学的身影,如图,折叠一张三角形纸片,把三角形的三个角拼在一起,就得到一个著名的几何定理,这一定理的内容是 .?
7. 在△ABC中,若∠A=∠B=∠C,则∠A= .?
8. 如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB= .?
9. 如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向.若∠ACB=80°,则C处在B处的北偏东 方向.?
10. 如图,小张从家(图中A处)出发,向南偏东40°的方向走到学校(图中B处),再从学校出发,向北偏西75°的方向走到小明家(图中C处),则∠ABC为 .?
11. 在△ABC中,2(∠A+∠B)=3∠C,求∠C的补角的度数.
12. 如图,有A,B,C三个小岛,B岛在A岛的北偏东85°方向,A岛在C岛的西南方向,B岛在C岛的南偏西20°方向,求∠ABC的度数.
13. 如图,在△ABC中,AD,BE分别是∠BAC,∠ABC的平分线.
(1)若∠C=70°,∠BAC=60°,则∠BED的度数是 ;?
(2)探究∠BED与∠C的数量关系,并证明你的结论.
14. 如图,在△ABC中,CD是∠ACB的平分线,CE是AB边上的高.
(1)若∠A=45°,∠B=75°,求∠DCE的度数;
(2)若∠A<∠B,试写出∠DCE与∠A,∠B之间的关系式,并说明理由.
15. (1)如图1,把△ABC纸片沿DE折叠,使点A落在四边形BCED内部点A'的位置.试写出∠A与∠1+∠2之间的关系,并说明理由.
(2)如图2,如果把△ABC纸片沿DE折叠,使点A落在四边形BCED外部点A'的位置.此时∠A与∠1,∠2之间存在怎样的数量关系?
(3)如图3,如果把四边形ABCD沿EF折叠,使点A,D分别落在四边形BCFE内部点A',D'的位置.∠A',∠D'与∠1,∠2之间又存在怎样的数量关系?
参考答案
1. B 2. A 3. B 4. B
5. 80°
6. 三角形三个内角的和等于180°
7. 30°
8. 90°
9. 85°
10. 35°
11. 解:∵2(∠A+∠B)=3∠C,∠A+∠B=180°-∠C,∴2(180°-∠C)=3∠C,∴∠C=72°,∴∠C的补角的度数为108°.
12. 解:由题意得∠DAB=85°,∠ACE=45°,∠BCE=20°,∴∠ACB=∠ACE-∠BCE=25°. 又∵AD∥CE,∴∠DAC=∠ACE=45°,∴∠CAB=∠DAB-∠DAC=40°,∴∠ABC=180°-∠CAB-∠ACB=115°.
13. 解:(1)55°
(2)∠BED=90°-∠C. 理由:∵AD,BE分别是∠BAC,∠ABC的平分线,∴∠ABE=∠ABC,∠BAE=∠BAC,∴∠BED=∠ABE+∠BAE=(∠ABC+∠BAC)=(180°-∠C)=90°-∠C.
14. 解:(1)∠DCE=15°.
(2)∠DCE=(∠B-∠A). 理由:在△ABC中,∠ACB=180°-∠A-∠B. ∵CD是∠ACB的平分线,∴∠ACD=∠ACB=(180°-∠A-∠B). ∵CE是AB边上的高,∴∠ACE=90°-∠A,∴∠DCE=∠ACE-∠ACD=90°-∠A-(180°-∠A-∠B)=(∠B-∠A).
15. 解:(1)2∠A=∠1+∠2. 理由:根据翻折的性质,得∠ADE=(180°-∠1),∠AED=(180°-∠2). ∵∠A+∠ADE+∠AED=180°,∴∠A+(180°-∠1)+(180°-∠2)=180°,整理得2∠A=∠1+∠2.
(2)根据翻折的性质,得∠ADE=(180°-∠1),∠AED=(180°+∠2). ∵∠A+∠ADE+∠AED=180°,∴∠A+(180°-∠1)+(180°+∠2)=180°,整理得2∠A=∠1-∠2.
(3)根据翻折的性质,得∠AEF=(180°-∠1),∠DFE=(180°-∠2). ∵∠A+∠D+∠AEF+∠
DFE=360°,∴∠A+∠D+(180°-∠1)+(180°-∠2)=360°,整理得2(∠A+∠D)=∠1+∠2+360°,即2(∠A'+∠D')=∠1+∠2+360°.
_21?????????è?????(www???21cnjy???com)_
人教版八年级数学上册课时作业
第十一章 三角形
11.2 与三角形有关的角
11.2.1 三角形的内角
第1课时 三角形的内角和
1. 如图是一块三角形木板的残余部分,量得∠A=110°,∠B=30°,则这块三角形木板缺少的角的度数是( )
A. 30° B. 40° C. 50° D. 60°
2. 如图,小明将文具盒里的一副三角板叠放在一起,则图中的∠α等于( )
A. 105° B. 115° C. 125° D. 135°
3. 如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于点E,∠BAC=60°,∠ABE=25°,则∠DAC的大小是( )
A. 15° B. 20° C. 25° D. 30°
4. 如图,在△ABC中,∠B,∠C的平分线BE,CD相交于点F.若∠BFC=116°,则∠A等于( )
A. 51° B. 52° C. 53° D. 58°
5. 如图,在△ABC中,∠A=60°,∠B=40°,则∠C= .?
6. 在我们的生活中处处有数学的身影,如图,折叠一张三角形纸片,把三角形的三个角拼在一起,就得到一个著名的几何定理,这一定理的内容是 .?
7. 在△ABC中,若∠A=∠B=∠C,则∠A= .?
8. 如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB= .?
9. 如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向.若∠ACB=80°,则C处在B处的北偏东 方向.?
10. 如图,小张从家(图中A处)出发,向南偏东40°的方向走到学校(图中B处),再从学校出发,向北偏西75°的方向走到小明家(图中C处),则∠ABC为 .?
11. 在△ABC中,2(∠A+∠B)=3∠C,求∠C的补角的度数.
12. 如图,有A,B,C三个小岛,B岛在A岛的北偏东85°方向,A岛在C岛的西南方向,B岛在C岛的南偏西20°方向,求∠ABC的度数.
13. 如图,在△ABC中,AD,BE分别是∠BAC,∠ABC的平分线.
(1)若∠C=70°,∠BAC=60°,则∠BED的度数是 ;?
(2)探究∠BED与∠C的数量关系,并证明你的结论.
14. 如图,在△ABC中,CD是∠ACB的平分线,CE是AB边上的高.
(1)若∠A=45°,∠B=75°,求∠DCE的度数;
(2)若∠A<∠B,试写出∠DCE与∠A,∠B之间的关系式,并说明理由.
15. (1)如图1,把△ABC纸片沿DE折叠,使点A落在四边形BCED内部点A'的位置.试写出∠A与∠1+∠2之间的关系,并说明理由.
(2)如图2,如果把△ABC纸片沿DE折叠,使点A落在四边形BCED外部点A'的位置.此时∠A与∠1,∠2之间存在怎样的数量关系?
(3)如图3,如果把四边形ABCD沿EF折叠,使点A,D分别落在四边形BCFE内部点A',D'的位置.∠A',∠D'与∠1,∠2之间又存在怎样的数量关系?
参考答案
1. B 2. A 3. B 4. B
5. 80°
6. 三角形三个内角的和等于180°
7. 30°
8. 90°
9. 85°
10. 35°
11. 解:∵2(∠A+∠B)=3∠C,∠A+∠B=180°-∠C,∴2(180°-∠C)=3∠C,∴∠C=72°,∴∠C的补角的度数为108°.
12. 解:由题意得∠DAB=85°,∠ACE=45°,∠BCE=20°,∴∠ACB=∠ACE-∠BCE=25°. 又∵AD∥CE,∴∠DAC=∠ACE=45°,∴∠CAB=∠DAB-∠DAC=40°,∴∠ABC=180°-∠CAB-∠ACB=115°.
13. 解:(1)55°
(2)∠BED=90°-∠C. 理由:∵AD,BE分别是∠BAC,∠ABC的平分线,∴∠ABE=∠ABC,∠BAE=∠BAC,∴∠BED=∠ABE+∠BAE=(∠ABC+∠BAC)=(180°-∠C)=90°-∠C.
14. 解:(1)∠DCE=15°.
(2)∠DCE=(∠B-∠A). 理由:在△ABC中,∠ACB=180°-∠A-∠B. ∵CD是∠ACB的平分线,∴∠ACD=∠ACB=(180°-∠A-∠B). ∵CE是AB边上的高,∴∠ACE=90°-∠A,∴∠DCE=∠ACE-∠ACD=90°-∠A-(180°-∠A-∠B)=(∠B-∠A).
15. 解:(1)2∠A=∠1+∠2. 理由:根据翻折的性质,得∠ADE=(180°-∠1),∠AED=(180°-∠2). ∵∠A+∠ADE+∠AED=180°,∴∠A+(180°-∠1)+(180°-∠2)=180°,整理得2∠A=∠1+∠2.
(2)根据翻折的性质,得∠ADE=(180°-∠1),∠AED=(180°+∠2). ∵∠A+∠ADE+∠AED=180°,∴∠A+(180°-∠1)+(180°+∠2)=180°,整理得2∠A=∠1-∠2.
(3)根据翻折的性质,得∠AEF=(180°-∠1),∠DFE=(180°-∠2). ∵∠A+∠D+∠AEF+∠
DFE=360°,∴∠A+∠D+(180°-∠1)+(180°-∠2)=360°,整理得2(∠A+∠D)=∠1+∠2+360°,即2(∠A'+∠D')=∠1+∠2+360°.
_21?????????è?????(www???21cnjy???com)_
