14.4.2用样本估计总体的离散程度参数用频率直方图估计总体分布同步练习-2020-2021学年高一下学期数学苏教版(2019)必修第二册(Word含答案解析)
文档属性
| 名称 | 14.4.2用样本估计总体的离散程度参数用频率直方图估计总体分布同步练习-2020-2021学年高一下学期数学苏教版(2019)必修第二册(Word含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 246.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 09:35:54 | ||
图片预览




文档简介
用样本估计总体的离散程度参数 用频率直方图估计总体分布
一、选择题
1.下列选项中,能反映一组数据的离散程度的是( )
A.平均数 B.中位数 C.方差 D.众数
2.对一组样本数据xi(i=1,2,…,n),如将它们改为xi-m(i=1,2,…,n),其中m≠0,则下面结论正确的是( )
A.平均数与方差都不变
B.平均数与方差都变了
C.平均数不变,方差变了
D.平均数变了,方差不变
3.样本中共有5个个体,其值分别为a,0,1,2,3.若该样本的平均数为1,则样本的标准差为( )
A. B. C.2 D.
4.高三学生李丽在一年的五次数学模拟考试中的成绩(单位:分)为:x,y,105,109,110.已知该同学五次数学成绩数据的平均数为108,方差为35.2,则|x-y|的值为( )
A.15 B.16 C.17 D.18
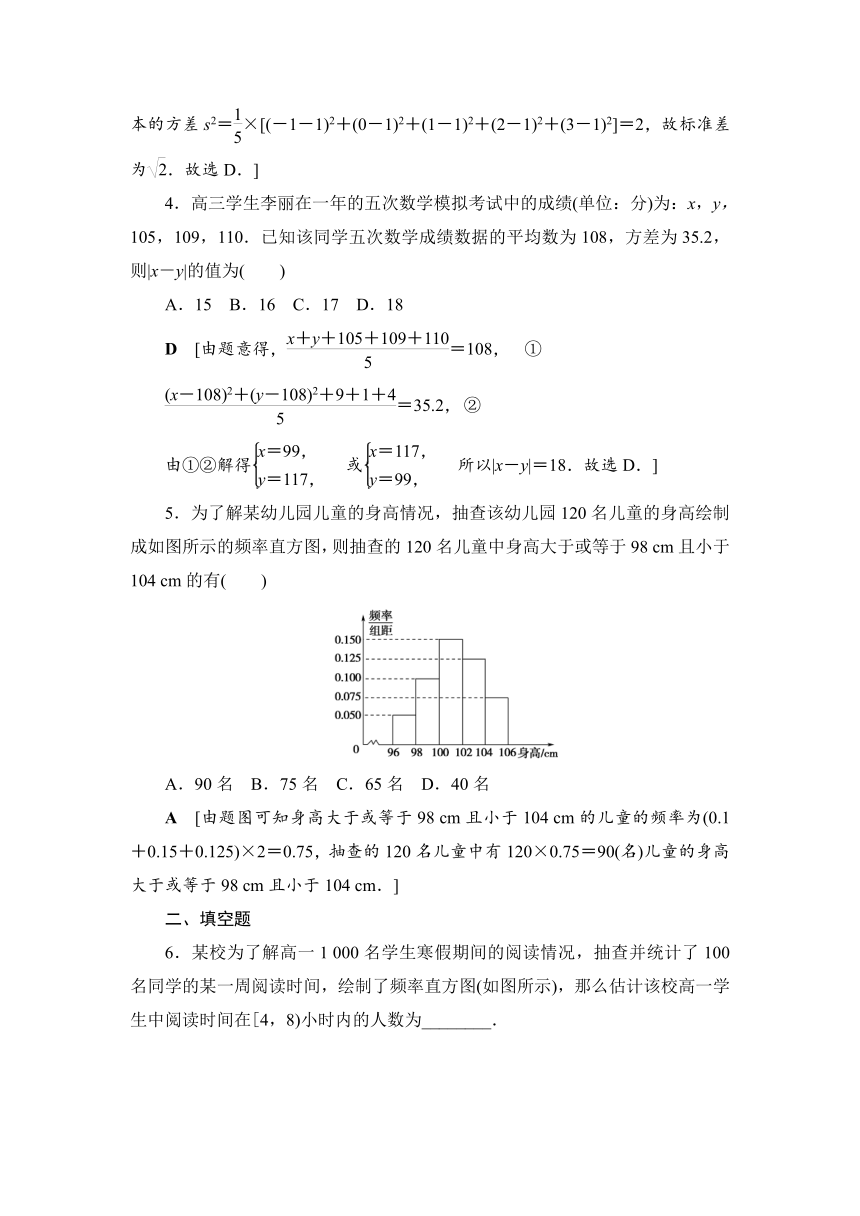
5.为了解某幼儿园儿童的身高情况,抽查该幼儿园120名儿童的身高绘制成如图所示的频率直方图,则抽查的120名儿童中身高大于或等于98 cm且小于104 cm的有( )
A.90名 B.75名 C.65名 D.40名
二、填空题
6.某校为了解高一1 000名学生寒假期间的阅读情况,抽查并统计了100名同学的某一周阅读时间,绘制了频率直方图(如图所示),那么估计该校高一学生中阅读时间在[4,8)小时内的人数为________.
7.五个数1,2,3,4,a的平均数是3,则a=________,这五个数的标准差是________.
8.为了调查公司员工的健康状况,用分层抽样的方法抽取样本,已知所抽取的所有员工的平均体重为60 kg,标准差为60,男员工的平均体重为70 kg,标准差为50,女员工的平均体重为50 kg,方差为60,若样本中有20名男员工,则女员工的人数为________.
三、解答题
9.为了保护学生的视力,教室内的日光灯在使用一段时间后必须更换.已知某校使用的100只日光灯在必须换掉前的使用天数如下表:
天数 151~
180 181~
210 211~
240 241~
270 271~
300 301~
330 331~
360 361~
390
灯管 数 1 11 18 20 25 16 7 2
(1)试估计这种日光灯的平均使用寿命;
(2)若定期更换,可选择多长时间统一更换合适?
10.某学校统计教师职称及年龄,中级职称教师的人数为50人,其平均年龄为38岁,方差是2,高级职称的教师3人58岁,5人40岁,2人38岁,求该校中级职称和高级职称教师年龄的平均数和方差.
能力过关
11.(多选题)甲、乙两班举行电脑汉字录入比赛,参赛学生每分钟录入汉字的个数经统计计算后填入下表:
班级 参加人数 中位数 方差 平均数
甲 55 149 191 135
乙 55 151 110 135
某同学根据表中数据分析得出的结论正确的是( )
A.甲、乙两班学生成绩的平均数相同
B.甲班的成绩波动比乙班的成绩波动大
C.乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字数≥150个为优秀)
D.甲班成绩的众数小于乙班成绩的众数
12.(多选题)在发生公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标准为“连续7天,每天新增疑似病例不超过5人”.过去7日,甲、乙、丙、丁四地新增疑似病例数据信息如下,则一定符合该标准的是( )
甲地:总体平均数≤3,且中位数为0;
乙地:总体平均数为2,且标准差s≤2;
丙地:总体平均数≤3,且极差c≤2;
丁地:众数为1,且极差c≤4.
A.甲地 B.乙地 C.丙地 D.丁地
13.某学员在一次射击测试中射靶10次,命中环数如下:7,8,7,9,5,4,9,10,7,4,
则平均命中环数为________;命中环数的标准差为________.
14.由正整数组成的一组数据x1,x2,x3,x4,其平均数和中位数都是2,且标准差等于1,则这组数据为________________(从小到大排列).
15.我国是世界上严重缺水的国家之一,某市为了制定合理的节水方案,对居民用水情况进行了调查.通过抽样,获得了某年100户居民每人的月均用水量(单位:吨).将数据按照[0,0.5),[0.5,1),… ,[4,4.5]分成9组,制成了如图所示的频率直方图.
(1)求直方图中a的值;
(2)用每组区间的中点作为每组用水量的平均值,这9组居民每人的月均用水量前4组的方差都为0.3,后5组的方差都为0.4,求这100户居民月均用水量的方差.
一、选择题
1.下列选项中,能反映一组数据的离散程度的是( )
A.平均数 B.中位数 C.方差 D.众数
C [由方差的定义,知方差反映了一组数据的离散程度.]
2.对一组样本数据xi(i=1,2,…,n),如将它们改为xi-m(i=1,2,…,n),其中m≠0,则下面结论正确的是( )
A.平均数与方差都不变
B.平均数与方差都变了
C.平均数不变,方差变了
D.平均数变了,方差不变
D [若x1,x2,…,xn的平均数为,方差为s2,则ax1+b,ax2+b,…,axn+b(a≠0)的平均数为a+b,方差为a2s2,标准差为,故选D.]
3.样本中共有5个个体,其值分别为a,0,1,2,3.若该样本的平均数为1,则样本的标准差为( )
A. B. C.2 D.
D [∵样本a,0,1,2,3的平均数为1,∴=1,解得a=-1.则样本的方差s2=×[(-1-1)2+(0-1)2+(1-1)2+(2-1)2+(3-1)2]=2,故标准差为.故选D.]
4.高三学生李丽在一年的五次数学模拟考试中的成绩(单位:分)为:x,y,105,109,110.已知该同学五次数学成绩数据的平均数为108,方差为35.2,则|x-y|的值为( )
A.15 B.16 C.17 D.18
D [由题意得,=108, ①
=35.2, ②
由①②解得或所以|x-y|=18.故选D.]
5.为了解某幼儿园儿童的身高情况,抽查该幼儿园120名儿童的身高绘制成如图所示的频率直方图,则抽查的120名儿童中身高大于或等于98 cm且小于104 cm的有( )
A.90名 B.75名 C.65名 D.40名
A [由题图可知身高大于或等于98 cm且小于104 cm的儿童的频率为(0.1+0.15+0.125)×2=0.75,抽查的120名儿童中有120×0.75=90(名)儿童的身高大于或等于98 cm且小于104 cm.]
二、填空题
6.某校为了解高一1 000名学生寒假期间的阅读情况,抽查并统计了100名同学的某一周阅读时间,绘制了频率直方图(如图所示),那么估计该校高一学生中阅读时间在[4,8)小时内的人数为________.
540 [根据频率直方图,可得阅读时间在[4,8)小时内的频率为(0.12+0.15)×2=0.54,所以估计该校高一学生中阅读时间在[4,8)小时内的人数为1 000×0.54=540.]
7.五个数1,2,3,4,a的平均数是3,则a=________,这五个数的标准差是________.
5 [由=3得a=5;
由s2=[(1-3)2+(2-3)2+(3-3)2+(4-3)2+(5-3)2]=2得,标准差s=.]
8.为了调查公司员工的健康状况,用分层抽样的方法抽取样本,已知所抽取的所有员工的平均体重为60 kg,标准差为60,男员工的平均体重为70 kg,标准差为50,女员工的平均体重为50 kg,方差为60,若样本中有20名男员工,则女员工的人数为________.
200 [设男,女员工的权重分别为ω男,ω女,
由题意可知s2=ω男[s+(男-)2]+ω女[s+(女-)2],
即ω男[502+(70-60)2]+(1-ω男)[602+(50-60)2]=602,解得ω男=,ω女=,
因为样本中有20名男员工,所有样本中女员工的人数为200.]
三、解答题
9.为了保护学生的视力,教室内的日光灯在使用一段时间后必须更换.已知某校使用的100只日光灯在必须换掉前的使用天数如下表:
天数 151~
180 181~
210 211~
240 241~
270 271~
300 301~
330 331~
360 361~
390
灯管 数 1 11 18 20 25 16 7 2
(1)试估计这种日光灯的平均使用寿命;
(2)若定期更换,可选择多长时间统一更换合适?
[解] (1)各组的组中值分别为165,195,225,255,285,315,345,375,由此可算得这种日光灯的平均使用寿命约为165×1%+195×11%+225×18%+255×20%+285×25%+315×16%+345×7%+375×2%=267.9≈268(天).
(2)×[1×(165-268)2+11×(195-268)2+18×(225-268)2+20×(255-268)2+25×(285-268)2+16× (315-268)2+7×(345-268)2+2×(375-268)2]=2 128.6.
故标准差为≈46.
估计这种日光灯的平均使用寿命约为268天,标准差约为46天,故在222天到314天之间统一更换较合适.
10.某学校统计教师职称及年龄,中级职称教师的人数为50人,其平均年龄为38岁,方差是2,高级职称的教师3人58岁,5人40岁,2人38岁,求该校中级职称和高级职称教师年龄的平均数和方差.
[解] 由已知条件可知高级职称教师的平均年龄为高==45,
年龄的方差为s=[3×(58-45)2+5×(40-45)2+2×(38-45)2]=73,
所以该校中级职称和高级职称教师的平均年龄为
=×38+×45≈39.2(岁),
该校中级职称和高级职称教师的年龄的方差是
s2=[2+(38-39.2)2]+[73+(45-39.2)2]=20.64.
能力过关
11.(多选题)甲、乙两班举行电脑汉字录入比赛,参赛学生每分钟录入汉字的个数经统计计算后填入下表:
班级 参加人数 中位数 方差 平均数
甲 55 149 191 135
乙 55 151 110 135
某同学根据表中数据分析得出的结论正确的是( )
A.甲、乙两班学生成绩的平均数相同
B.甲班的成绩波动比乙班的成绩波动大
C.乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字数≥150个为优秀)
D.甲班成绩的众数小于乙班成绩的众数
ABC [甲、乙两班学生成绩的平均数都是135,故两班成绩的平均数相同,∴A正确;s=191>110=s,∴甲班成绩不如乙班稳定,即甲班的成绩波动较大,∴B正确;甲、乙两班人数相同,但甲班的中位数为149,乙班的中位数为151,从而易知乙班不少于150个的人数要多于甲班,∴C正确;由题表看不出两班学生成绩的众数,∴D错误.]
12.(多选题)在发生公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标准为“连续7天,每天新增疑似病例不超过5人”.过去7日,甲、乙、丙、丁四地新增疑似病例数据信息如下,则一定符合该标准的是( )
甲地:总体平均数≤3,且中位数为0;
乙地:总体平均数为2,且标准差s≤2;
丙地:总体平均数≤3,且极差c≤2;
丁地:众数为1,且极差c≤4.
A.甲地 B.乙地 C.丙地 D.丁地
CD [甲地:满足总体平均数≤3,且中位数为0,举例7天的新增疑似病例为0,0,0,0,5,6,7,则不符合该标准;乙地:若7天新增疑似病例为1,1,1,1,2,2,6,满足平均数为2,标准差小于2,但不符合该标准;丙地:由极差c≤2可知,若新增疑似病例超过5人,比如6人,那么最小值不低于4,总体平均数就会大于3,故每天新增疑似病例不超过5人,丙地符合该标准;丁地:因为众数为1,且极差c≤4,所以新增疑似病例的最大值不超过5,所以丁地符合.故选CD.]
13.某学员在一次射击测试中射靶10次,命中环数如下:7,8,7,9,5,4,9,10,7,4,
则平均命中环数为________;命中环数的标准差为________.
7 2 [==7.
∵s2=[(7-7)2+(8-7)2+(7-7)2+(9-7)2+(5-7)2+(4-7)2+(9-7)2+(10-7)2+(7-7)2+(4-7)2]=4,∴s=2.]
14.由正整数组成的一组数据x1,x2,x3,x4,其平均数和中位数都是2,且标准差等于1,则这组数据为________________(从小到大排列).
1,1,3,3 [不妨设x1≤x2≤x3≤x4且x1,x2,x3,x4为正整数.
由条件知
即
又x1,x2,x3,x4为正整数,
∴x1=x2=x3=x4=2或x1=1,x2=x3=2,x4=3或x1=x2=1,x3=x4=3.
∵s==1,
∴x1=x2=1,x3=x4=3. 由此可得4个数分别为1,1,3,3.]
15.我国是世界上严重缺水的国家之一,某市为了制定合理的节水方案,对居民用水情况进行了调查.通过抽样,获得了某年100户居民每人的月均用水量(单位:吨).将数据按照[0,0.5),[0.5,1),… ,[4,4.5]分成9组,制成了如图所示的频率直方图.
(1)求直方图中a的值;
(2)用每组区间的中点作为每组用水量的平均值,这9组居民每人的月均用水量前4组的方差都为0.3,后5组的方差都为0.4,求这100户居民月均用水量的方差.
[解] (1)由频率直方图可知,月均用水量在[0,0.5)内的频率为0.08×0.5=0.04,同理,在[0.5,1),[1.5, 2),[2, 2.5),[3,3.5),[3.5,4),[4,4.5]内的频率分别为0.08,0.21,0.25,0.06,0.04,0.02.
由1-(0.04+0.08+0.21+0.25+0.06+0.04+0.02)=2a×0.5,解得a=0.30.
(2)由题意可知,这9组月均用水量的平均数依次是1=0.25,2=0.75,3=1.25,4=1.75,5=2.25,6=2.75,7=3.25,8=3.75,9=4.25,
这100户居民的月均用水量为=0.04×0.25+0.08×0.75+0.15×1.25+0.21×1.75+0.25×2.25+0.15×2.75+0.06×3.25+0.04×3.75+0.02×4.25=2.03,
则这100户居民月均用水量的方差为
s2=0.04×[0.3+(0.25-2.03)2]+0.08×[0.3+(0.75-2.03)2]+0.15× [0.3+(1.25-2.03)2]+0.21× [0.3+(1.75-2.03)2]+0.25×[0.4+(2.25-2.03)2]+0.15×[0.4+(2.75-2.03)2]+0.06×[0.4+(3.25-2.03)2]+0.04×[0.4+(3.75-2.03)2]+0.02×[0.4+(4.25-2.03)2]=1.113 6.
一、选择题
1.下列选项中,能反映一组数据的离散程度的是( )
A.平均数 B.中位数 C.方差 D.众数
2.对一组样本数据xi(i=1,2,…,n),如将它们改为xi-m(i=1,2,…,n),其中m≠0,则下面结论正确的是( )
A.平均数与方差都不变
B.平均数与方差都变了
C.平均数不变,方差变了
D.平均数变了,方差不变
3.样本中共有5个个体,其值分别为a,0,1,2,3.若该样本的平均数为1,则样本的标准差为( )
A. B. C.2 D.
4.高三学生李丽在一年的五次数学模拟考试中的成绩(单位:分)为:x,y,105,109,110.已知该同学五次数学成绩数据的平均数为108,方差为35.2,则|x-y|的值为( )
A.15 B.16 C.17 D.18
5.为了解某幼儿园儿童的身高情况,抽查该幼儿园120名儿童的身高绘制成如图所示的频率直方图,则抽查的120名儿童中身高大于或等于98 cm且小于104 cm的有( )
A.90名 B.75名 C.65名 D.40名
二、填空题
6.某校为了解高一1 000名学生寒假期间的阅读情况,抽查并统计了100名同学的某一周阅读时间,绘制了频率直方图(如图所示),那么估计该校高一学生中阅读时间在[4,8)小时内的人数为________.
7.五个数1,2,3,4,a的平均数是3,则a=________,这五个数的标准差是________.
8.为了调查公司员工的健康状况,用分层抽样的方法抽取样本,已知所抽取的所有员工的平均体重为60 kg,标准差为60,男员工的平均体重为70 kg,标准差为50,女员工的平均体重为50 kg,方差为60,若样本中有20名男员工,则女员工的人数为________.
三、解答题
9.为了保护学生的视力,教室内的日光灯在使用一段时间后必须更换.已知某校使用的100只日光灯在必须换掉前的使用天数如下表:
天数 151~
180 181~
210 211~
240 241~
270 271~
300 301~
330 331~
360 361~
390
灯管 数 1 11 18 20 25 16 7 2
(1)试估计这种日光灯的平均使用寿命;
(2)若定期更换,可选择多长时间统一更换合适?
10.某学校统计教师职称及年龄,中级职称教师的人数为50人,其平均年龄为38岁,方差是2,高级职称的教师3人58岁,5人40岁,2人38岁,求该校中级职称和高级职称教师年龄的平均数和方差.
能力过关
11.(多选题)甲、乙两班举行电脑汉字录入比赛,参赛学生每分钟录入汉字的个数经统计计算后填入下表:
班级 参加人数 中位数 方差 平均数
甲 55 149 191 135
乙 55 151 110 135
某同学根据表中数据分析得出的结论正确的是( )
A.甲、乙两班学生成绩的平均数相同
B.甲班的成绩波动比乙班的成绩波动大
C.乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字数≥150个为优秀)
D.甲班成绩的众数小于乙班成绩的众数
12.(多选题)在发生公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标准为“连续7天,每天新增疑似病例不超过5人”.过去7日,甲、乙、丙、丁四地新增疑似病例数据信息如下,则一定符合该标准的是( )
甲地:总体平均数≤3,且中位数为0;
乙地:总体平均数为2,且标准差s≤2;
丙地:总体平均数≤3,且极差c≤2;
丁地:众数为1,且极差c≤4.
A.甲地 B.乙地 C.丙地 D.丁地
13.某学员在一次射击测试中射靶10次,命中环数如下:7,8,7,9,5,4,9,10,7,4,
则平均命中环数为________;命中环数的标准差为________.
14.由正整数组成的一组数据x1,x2,x3,x4,其平均数和中位数都是2,且标准差等于1,则这组数据为________________(从小到大排列).
15.我国是世界上严重缺水的国家之一,某市为了制定合理的节水方案,对居民用水情况进行了调查.通过抽样,获得了某年100户居民每人的月均用水量(单位:吨).将数据按照[0,0.5),[0.5,1),… ,[4,4.5]分成9组,制成了如图所示的频率直方图.
(1)求直方图中a的值;
(2)用每组区间的中点作为每组用水量的平均值,这9组居民每人的月均用水量前4组的方差都为0.3,后5组的方差都为0.4,求这100户居民月均用水量的方差.
一、选择题
1.下列选项中,能反映一组数据的离散程度的是( )
A.平均数 B.中位数 C.方差 D.众数
C [由方差的定义,知方差反映了一组数据的离散程度.]
2.对一组样本数据xi(i=1,2,…,n),如将它们改为xi-m(i=1,2,…,n),其中m≠0,则下面结论正确的是( )
A.平均数与方差都不变
B.平均数与方差都变了
C.平均数不变,方差变了
D.平均数变了,方差不变
D [若x1,x2,…,xn的平均数为,方差为s2,则ax1+b,ax2+b,…,axn+b(a≠0)的平均数为a+b,方差为a2s2,标准差为,故选D.]
3.样本中共有5个个体,其值分别为a,0,1,2,3.若该样本的平均数为1,则样本的标准差为( )
A. B. C.2 D.
D [∵样本a,0,1,2,3的平均数为1,∴=1,解得a=-1.则样本的方差s2=×[(-1-1)2+(0-1)2+(1-1)2+(2-1)2+(3-1)2]=2,故标准差为.故选D.]
4.高三学生李丽在一年的五次数学模拟考试中的成绩(单位:分)为:x,y,105,109,110.已知该同学五次数学成绩数据的平均数为108,方差为35.2,则|x-y|的值为( )
A.15 B.16 C.17 D.18
D [由题意得,=108, ①
=35.2, ②
由①②解得或所以|x-y|=18.故选D.]
5.为了解某幼儿园儿童的身高情况,抽查该幼儿园120名儿童的身高绘制成如图所示的频率直方图,则抽查的120名儿童中身高大于或等于98 cm且小于104 cm的有( )
A.90名 B.75名 C.65名 D.40名
A [由题图可知身高大于或等于98 cm且小于104 cm的儿童的频率为(0.1+0.15+0.125)×2=0.75,抽查的120名儿童中有120×0.75=90(名)儿童的身高大于或等于98 cm且小于104 cm.]
二、填空题
6.某校为了解高一1 000名学生寒假期间的阅读情况,抽查并统计了100名同学的某一周阅读时间,绘制了频率直方图(如图所示),那么估计该校高一学生中阅读时间在[4,8)小时内的人数为________.
540 [根据频率直方图,可得阅读时间在[4,8)小时内的频率为(0.12+0.15)×2=0.54,所以估计该校高一学生中阅读时间在[4,8)小时内的人数为1 000×0.54=540.]
7.五个数1,2,3,4,a的平均数是3,则a=________,这五个数的标准差是________.
5 [由=3得a=5;
由s2=[(1-3)2+(2-3)2+(3-3)2+(4-3)2+(5-3)2]=2得,标准差s=.]
8.为了调查公司员工的健康状况,用分层抽样的方法抽取样本,已知所抽取的所有员工的平均体重为60 kg,标准差为60,男员工的平均体重为70 kg,标准差为50,女员工的平均体重为50 kg,方差为60,若样本中有20名男员工,则女员工的人数为________.
200 [设男,女员工的权重分别为ω男,ω女,
由题意可知s2=ω男[s+(男-)2]+ω女[s+(女-)2],
即ω男[502+(70-60)2]+(1-ω男)[602+(50-60)2]=602,解得ω男=,ω女=,
因为样本中有20名男员工,所有样本中女员工的人数为200.]
三、解答题
9.为了保护学生的视力,教室内的日光灯在使用一段时间后必须更换.已知某校使用的100只日光灯在必须换掉前的使用天数如下表:
天数 151~
180 181~
210 211~
240 241~
270 271~
300 301~
330 331~
360 361~
390
灯管 数 1 11 18 20 25 16 7 2
(1)试估计这种日光灯的平均使用寿命;
(2)若定期更换,可选择多长时间统一更换合适?
[解] (1)各组的组中值分别为165,195,225,255,285,315,345,375,由此可算得这种日光灯的平均使用寿命约为165×1%+195×11%+225×18%+255×20%+285×25%+315×16%+345×7%+375×2%=267.9≈268(天).
(2)×[1×(165-268)2+11×(195-268)2+18×(225-268)2+20×(255-268)2+25×(285-268)2+16× (315-268)2+7×(345-268)2+2×(375-268)2]=2 128.6.
故标准差为≈46.
估计这种日光灯的平均使用寿命约为268天,标准差约为46天,故在222天到314天之间统一更换较合适.
10.某学校统计教师职称及年龄,中级职称教师的人数为50人,其平均年龄为38岁,方差是2,高级职称的教师3人58岁,5人40岁,2人38岁,求该校中级职称和高级职称教师年龄的平均数和方差.
[解] 由已知条件可知高级职称教师的平均年龄为高==45,
年龄的方差为s=[3×(58-45)2+5×(40-45)2+2×(38-45)2]=73,
所以该校中级职称和高级职称教师的平均年龄为
=×38+×45≈39.2(岁),
该校中级职称和高级职称教师的年龄的方差是
s2=[2+(38-39.2)2]+[73+(45-39.2)2]=20.64.
能力过关
11.(多选题)甲、乙两班举行电脑汉字录入比赛,参赛学生每分钟录入汉字的个数经统计计算后填入下表:
班级 参加人数 中位数 方差 平均数
甲 55 149 191 135
乙 55 151 110 135
某同学根据表中数据分析得出的结论正确的是( )
A.甲、乙两班学生成绩的平均数相同
B.甲班的成绩波动比乙班的成绩波动大
C.乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字数≥150个为优秀)
D.甲班成绩的众数小于乙班成绩的众数
ABC [甲、乙两班学生成绩的平均数都是135,故两班成绩的平均数相同,∴A正确;s=191>110=s,∴甲班成绩不如乙班稳定,即甲班的成绩波动较大,∴B正确;甲、乙两班人数相同,但甲班的中位数为149,乙班的中位数为151,从而易知乙班不少于150个的人数要多于甲班,∴C正确;由题表看不出两班学生成绩的众数,∴D错误.]
12.(多选题)在发生公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标准为“连续7天,每天新增疑似病例不超过5人”.过去7日,甲、乙、丙、丁四地新增疑似病例数据信息如下,则一定符合该标准的是( )
甲地:总体平均数≤3,且中位数为0;
乙地:总体平均数为2,且标准差s≤2;
丙地:总体平均数≤3,且极差c≤2;
丁地:众数为1,且极差c≤4.
A.甲地 B.乙地 C.丙地 D.丁地
CD [甲地:满足总体平均数≤3,且中位数为0,举例7天的新增疑似病例为0,0,0,0,5,6,7,则不符合该标准;乙地:若7天新增疑似病例为1,1,1,1,2,2,6,满足平均数为2,标准差小于2,但不符合该标准;丙地:由极差c≤2可知,若新增疑似病例超过5人,比如6人,那么最小值不低于4,总体平均数就会大于3,故每天新增疑似病例不超过5人,丙地符合该标准;丁地:因为众数为1,且极差c≤4,所以新增疑似病例的最大值不超过5,所以丁地符合.故选CD.]
13.某学员在一次射击测试中射靶10次,命中环数如下:7,8,7,9,5,4,9,10,7,4,
则平均命中环数为________;命中环数的标准差为________.
7 2 [==7.
∵s2=[(7-7)2+(8-7)2+(7-7)2+(9-7)2+(5-7)2+(4-7)2+(9-7)2+(10-7)2+(7-7)2+(4-7)2]=4,∴s=2.]
14.由正整数组成的一组数据x1,x2,x3,x4,其平均数和中位数都是2,且标准差等于1,则这组数据为________________(从小到大排列).
1,1,3,3 [不妨设x1≤x2≤x3≤x4且x1,x2,x3,x4为正整数.
由条件知
即
又x1,x2,x3,x4为正整数,
∴x1=x2=x3=x4=2或x1=1,x2=x3=2,x4=3或x1=x2=1,x3=x4=3.
∵s==1,
∴x1=x2=1,x3=x4=3. 由此可得4个数分别为1,1,3,3.]
15.我国是世界上严重缺水的国家之一,某市为了制定合理的节水方案,对居民用水情况进行了调查.通过抽样,获得了某年100户居民每人的月均用水量(单位:吨).将数据按照[0,0.5),[0.5,1),… ,[4,4.5]分成9组,制成了如图所示的频率直方图.
(1)求直方图中a的值;
(2)用每组区间的中点作为每组用水量的平均值,这9组居民每人的月均用水量前4组的方差都为0.3,后5组的方差都为0.4,求这100户居民月均用水量的方差.
[解] (1)由频率直方图可知,月均用水量在[0,0.5)内的频率为0.08×0.5=0.04,同理,在[0.5,1),[1.5, 2),[2, 2.5),[3,3.5),[3.5,4),[4,4.5]内的频率分别为0.08,0.21,0.25,0.06,0.04,0.02.
由1-(0.04+0.08+0.21+0.25+0.06+0.04+0.02)=2a×0.5,解得a=0.30.
(2)由题意可知,这9组月均用水量的平均数依次是1=0.25,2=0.75,3=1.25,4=1.75,5=2.25,6=2.75,7=3.25,8=3.75,9=4.25,
这100户居民的月均用水量为=0.04×0.25+0.08×0.75+0.15×1.25+0.21×1.75+0.25×2.25+0.15×2.75+0.06×3.25+0.04×3.75+0.02×4.25=2.03,
则这100户居民月均用水量的方差为
s2=0.04×[0.3+(0.25-2.03)2]+0.08×[0.3+(0.75-2.03)2]+0.15× [0.3+(1.25-2.03)2]+0.21× [0.3+(1.75-2.03)2]+0.25×[0.4+(2.25-2.03)2]+0.15×[0.4+(2.75-2.03)2]+0.06×[0.4+(3.25-2.03)2]+0.04×[0.4+(3.75-2.03)2]+0.02×[0.4+(4.25-2.03)2]=1.113 6.
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
