2021-2022学年湘教版数学九年级上册3.6 位似 课件(共22张PPT)
文档属性
| 名称 | 2021-2022学年湘教版数学九年级上册3.6 位似 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 869.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
湘教版·
数学·
九年级(上)
3.6
位似
第三章
图形的相似
1.掌握位似图形的定义、性质及其画法。
2.学会位似图形的作图。
3.使学生经历对位似图形的观察、作图、分析、交流,体验探索得出数学结论的过程。
学习目标
位似图形的特征:
(1)是相似图形,
(2)每组对应点的连线交于一点.
位似图形的性质:
位似图形上任意一对对应点到位似中心的距离之比等于位似比.
合作探究
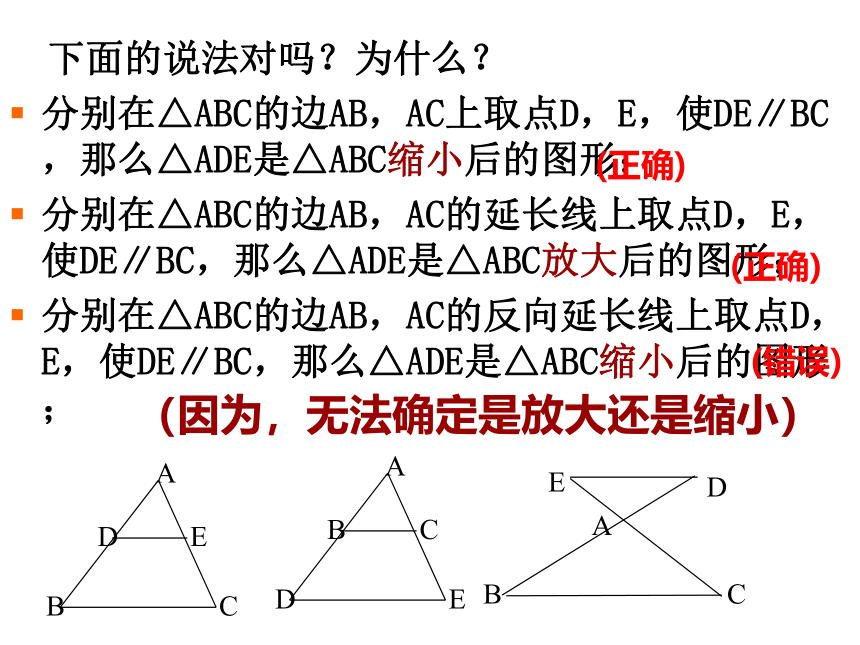
下面的说法对吗?为什么?
分别在△ABC的边AB,AC上取点D,E,使DE∥BC,那么△ADE是△ABC缩小后的图形;
分别在△ABC的边AB,AC的延长线上取点D,E,使DE∥BC,那么△ADE是△ABC放大后的图形;
分别在△ABC的边AB,AC的反向延长线上取点D,E,使DE∥BC,那么△ADE是△ABC缩小后的图形;
A
B
C
D
E
A
D
E
B
C
E
D
C
B
A
(正确)
(正确)
(错误)
(因为,无法确定是放大还是缩小)
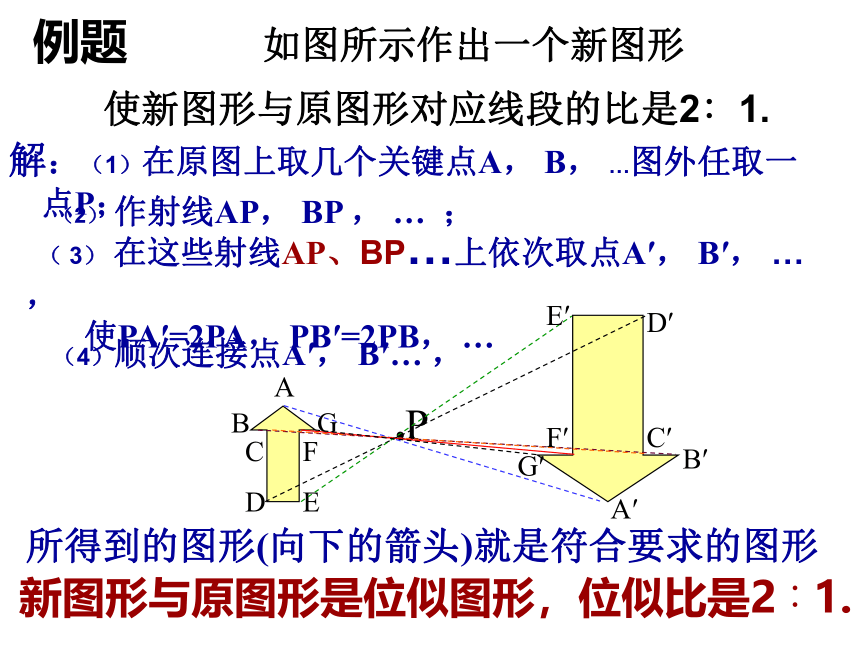
例题
使新图形与原图形对应线段的比是2∶1.
A
B
G
C
E
D
F
●P
解:(1)在原图上取几个关键点A,
B,
…图外任取一点P;
(2)
作射线AP,
BP
,
…
;
(
3)
在这些射线AP、BP…上依次取点A′,
B′,
…,
使PA′=2PA,
PB′=2PB,
…
B′
A′
C′
D′
E′
F′
G′
所得到的图形(向下的箭头)就是符合要求的图形
新图形与原图形是位似图形,位似比是2∶1.
如图所示作出一个新图形
(4)顺次连接点A′,
B′…
,
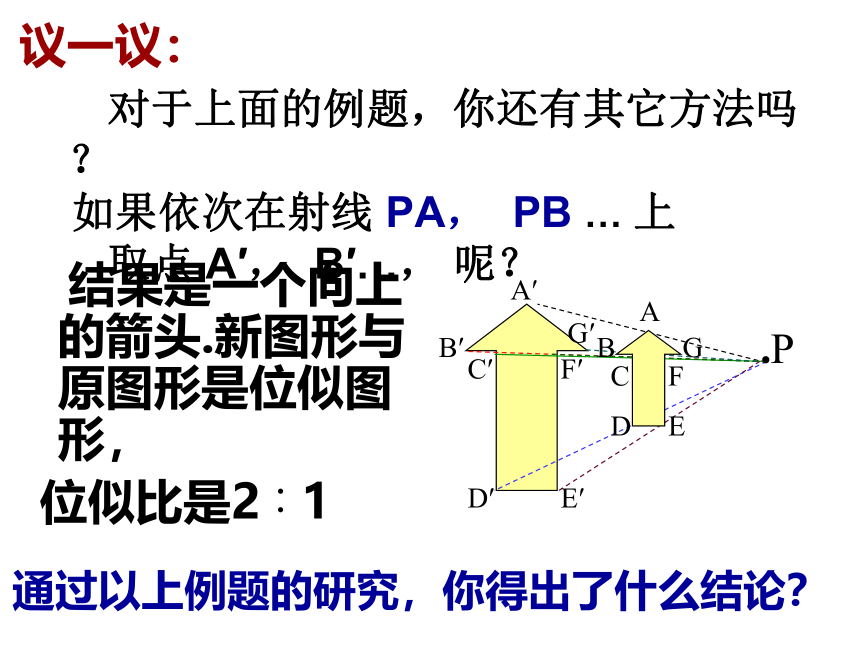
对于上面的例题,你还有其它方法吗?
如果依次在射线
PA,
PB
…
上
取点
A′,
B′…,
呢?
结果是一个向上的箭头.新图形与原图形是位似图形,
位似比是2∶1
A′
B′
C′
D′
E′
F′
G′
A
B
G
C
E
D
F
●P
议一议:
通过以上例题的研究,你得出了什么结论?
(1)在位似中心的同侧,两位似图形同向;
(2)在位似中心的异侧,两位似图形反向.
(由题目条件定位置)
作位似图形一般有以下两种情况:
练习:
作出一个新图形,使新图形与原图形对应线段的比为2:1,且新图形与原图形同向.
o
A
B
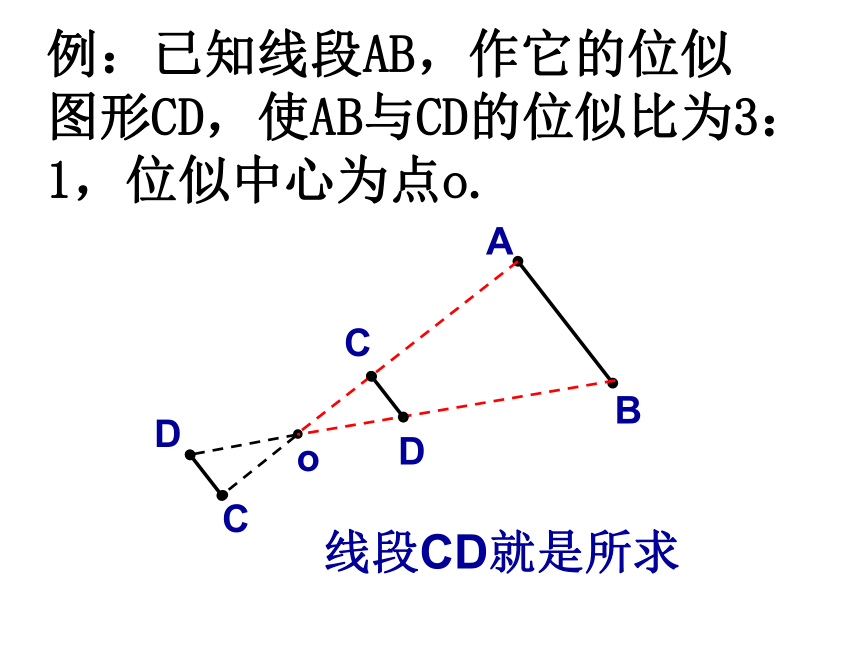
例:已知线段AB,作它的位似图形CD,使AB与CD的位似比为3:1,位似中心为点o.
C
D
C
D
线段CD就是所求
A
B
C
D
△DEF就是所求
D
O
例:已知△ABC,作它的位似图形△DEF,使△DEF与△ABC位似比为2:3,位似中心为点o.
E
F
E
F
练习:
三角形的顶点坐标分别是
A(2,2)B(4,2)C(6,4)
试将△ABC缩小,使缩小后的△DEF与△ABC对应边的比为1:2.
作位似图形的方法:
(2)找关键点;
(3)把位似比转换为对应点到位似中心的距离之比,找出关键点的对应点.
(1)确定所作图形是放大还是缩小,正像还是倒像;
(4)写出结论.
归纳新知
1.下列命题中,正确的是(
)
A.全等的图形一定是位似图形
B.相似图形一定是位似图形
C.位似图形一定是全等图形
D.位似图形一定是相似图形
D
课后练习
2.下列选项的两个相似图形中,不是位似图形的是(
)
A
3.图中的两个四边形是位似图形,它们的位似中心是(
)
A.点M
B.点N
C.点O
D.点P
D
4.小张用手机拍摄得到图①,经放大后得到图②,图①中线段AB在图②中的对应线段是(
)
A.FC
B.EH
C.EF
D.FH
C
5.如图,△ABC与△A′B′C′是位似图形,PB′=BB′,A′B′=2,则AB的长为(
)
A.1
B.2
C.4
D.8
C
6.如图,四边形ABCD和四边形A′B′C′D′是以点O为位似中心的位似图形,若OA∶OA′=2∶3,四边形ABCD的面积等于4,则四边形A′B′C′D′的面积为(
)
A.3
B.4
C.6
D.9
D
7.如图所示是△ABC位似图形的几种画法,其中正确的个数是(
)
A.1
B.2
C.3
D.4
C
8.如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA′∶OA=3∶5,四边形A′B′C′D′的面积为9
cm2,则四边形ABCD的面积为____cm2.
25
9.如图,已知△ADE和△ABC是位似图形,∠A=30°,DE垂直平分AC,且DE=2.
(1)求∠C的度数;
(2)求BC的长度.
10.如图,△EFD和△CFB是以点F为位似中心的位似图形,EF∶FC=1∶2,若S△EFD=1,求四边形EBCD的面积.
湘教版·
数学·
九年级(上)
3.6
位似
第三章
图形的相似
1.掌握位似图形的定义、性质及其画法。
2.学会位似图形的作图。
3.使学生经历对位似图形的观察、作图、分析、交流,体验探索得出数学结论的过程。
学习目标
位似图形的特征:
(1)是相似图形,
(2)每组对应点的连线交于一点.
位似图形的性质:
位似图形上任意一对对应点到位似中心的距离之比等于位似比.
合作探究
下面的说法对吗?为什么?
分别在△ABC的边AB,AC上取点D,E,使DE∥BC,那么△ADE是△ABC缩小后的图形;
分别在△ABC的边AB,AC的延长线上取点D,E,使DE∥BC,那么△ADE是△ABC放大后的图形;
分别在△ABC的边AB,AC的反向延长线上取点D,E,使DE∥BC,那么△ADE是△ABC缩小后的图形;
A
B
C
D
E
A
D
E
B
C
E
D
C
B
A
(正确)
(正确)
(错误)
(因为,无法确定是放大还是缩小)
例题
使新图形与原图形对应线段的比是2∶1.
A
B
G
C
E
D
F
●P
解:(1)在原图上取几个关键点A,
B,
…图外任取一点P;
(2)
作射线AP,
BP
,
…
;
(
3)
在这些射线AP、BP…上依次取点A′,
B′,
…,
使PA′=2PA,
PB′=2PB,
…
B′
A′
C′
D′
E′
F′
G′
所得到的图形(向下的箭头)就是符合要求的图形
新图形与原图形是位似图形,位似比是2∶1.
如图所示作出一个新图形
(4)顺次连接点A′,
B′…
,
对于上面的例题,你还有其它方法吗?
如果依次在射线
PA,
PB
…
上
取点
A′,
B′…,
呢?
结果是一个向上的箭头.新图形与原图形是位似图形,
位似比是2∶1
A′
B′
C′
D′
E′
F′
G′
A
B
G
C
E
D
F
●P
议一议:
通过以上例题的研究,你得出了什么结论?
(1)在位似中心的同侧,两位似图形同向;
(2)在位似中心的异侧,两位似图形反向.
(由题目条件定位置)
作位似图形一般有以下两种情况:
练习:
作出一个新图形,使新图形与原图形对应线段的比为2:1,且新图形与原图形同向.
o
A
B
例:已知线段AB,作它的位似图形CD,使AB与CD的位似比为3:1,位似中心为点o.
C
D
C
D
线段CD就是所求
A
B
C
D
△DEF就是所求
D
O
例:已知△ABC,作它的位似图形△DEF,使△DEF与△ABC位似比为2:3,位似中心为点o.
E
F
E
F
练习:
三角形的顶点坐标分别是
A(2,2)B(4,2)C(6,4)
试将△ABC缩小,使缩小后的△DEF与△ABC对应边的比为1:2.
作位似图形的方法:
(2)找关键点;
(3)把位似比转换为对应点到位似中心的距离之比,找出关键点的对应点.
(1)确定所作图形是放大还是缩小,正像还是倒像;
(4)写出结论.
归纳新知
1.下列命题中,正确的是(
)
A.全等的图形一定是位似图形
B.相似图形一定是位似图形
C.位似图形一定是全等图形
D.位似图形一定是相似图形
D
课后练习
2.下列选项的两个相似图形中,不是位似图形的是(
)
A
3.图中的两个四边形是位似图形,它们的位似中心是(
)
A.点M
B.点N
C.点O
D.点P
D
4.小张用手机拍摄得到图①,经放大后得到图②,图①中线段AB在图②中的对应线段是(
)
A.FC
B.EH
C.EF
D.FH
C
5.如图,△ABC与△A′B′C′是位似图形,PB′=BB′,A′B′=2,则AB的长为(
)
A.1
B.2
C.4
D.8
C
6.如图,四边形ABCD和四边形A′B′C′D′是以点O为位似中心的位似图形,若OA∶OA′=2∶3,四边形ABCD的面积等于4,则四边形A′B′C′D′的面积为(
)
A.3
B.4
C.6
D.9
D
7.如图所示是△ABC位似图形的几种画法,其中正确的个数是(
)
A.1
B.2
C.3
D.4
C
8.如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA′∶OA=3∶5,四边形A′B′C′D′的面积为9
cm2,则四边形ABCD的面积为____cm2.
25
9.如图,已知△ADE和△ABC是位似图形,∠A=30°,DE垂直平分AC,且DE=2.
(1)求∠C的度数;
(2)求BC的长度.
10.如图,△EFD和△CFB是以点F为位似中心的位似图形,EF∶FC=1∶2,若S△EFD=1,求四边形EBCD的面积.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
