山东省威海市环翠区2019-2020学年七年级上学期期末数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 山东省威海市环翠区2019-2020学年七年级上学期期末数学试卷(五四学制)(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 286.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 10:42:40 | ||
图片预览



文档简介
2019-2020学年山东省威海市环翠区七年级(上)期末数学试卷(五四学制)
一.选择题
1.下列说法正确的是( )
A.带根号的数都是无理数
B.无限小数都是无理数
C.两个无理数之和一定是无理数
D.两个无理数之积不一定是无理数
2.下列各式正确的是( )
A.=﹣2
B.(﹣)2=
C.=﹣2
D.(﹣)3=﹣6
3.已知点(﹣2,y1),(1,y2)都在一次函数y=kx﹣1(k<0)的图象上,则y1,y2的大小关系是( )
A.y1>y2
B.y1<y2
C.y1=y2
D.无法确定
4.如图,点D是△ABC内一点,∠D=105°,∠1=∠2,则∠ACB的度数为( )
A.65°
B.70°
C.75°
D.80°
5.函数y=2x+2的图象如图所示,下列说法正确的是( )
A.当x>0时,y>2
B.当x<0时,y<0
C.当x>0时,y>0
D.当x>﹣1时,y>2
6.通过估算比较下列两个数的大小,其中正确的是( )
A.<
B.﹣<
C.<
D.<24
7.AB⊥BC,EC⊥BC,AD⊥DE,AD=DE,AB=3,BC=8,则CE长为( )
A.4
B.5
C.8
D.10
8.如图,若OA=2,OA与x轴负半轴的夹角是30°,则点A关于x轴的对称点A′的坐标为( )
A.(﹣,1)
B.(﹣,﹣1)
C.(,1)
D.(﹣,1)
9.AD是△ABC的中线,∠ADB=45°,把△ADB沿直线AD翻折,点B落在B′的位置,BC=2,则CB′的长为( )
A.
B.2
C.
D.2
10.如图,在△ABC和△DEC中,已知AB=DE,∠A=∠D,还需添加一个条件才能使△ABC≌△DEC,不能添加的条件是( )
A.∠ECB=∠DCA
B.BC=EC
C.∠B=∠E
D.DC=AC
11.点P(m+3,m﹣1)在x轴上,则点P的坐标为( )
A.(0,﹣4)
B.(﹣3,0)
C.(﹣3,1)
D.(4,0)
12.已知A,B两地相距400km,某人驾车从A地到B地,途中加油一次.已知油箱中剩余油量y(L)与行驶路程x(km)之间的关系如图所示,假设汽车每100km耗油量保持不变,以下说法错误的是( )
A.出发时油箱中有20L油
B.途中加油30L
C.该汽车每100km耗油7.5L
D.汽车到达B地时油箱中还剩油15L
二.填空题
13.﹣27的立方根与的平方根的和是
.
14.在平面直角坐标系中,将直线y=2x+6向右平移两个单位得到直线l,则直线l的表达式是
.
15.已知点P的坐标为(1+a,2a﹣2),且点P到两坐标轴的距离相等,则a的值是
.
16.如图,在3×2的正方形网格中,已有两个小正方形被涂黑,再将其余小正方形涂黑一个,使整个图案构成一个轴对称图形的涂法有
种.
17.将腰长分别是2和1的两个等腰直角三角板按如图所示摆放,则AA′=
.
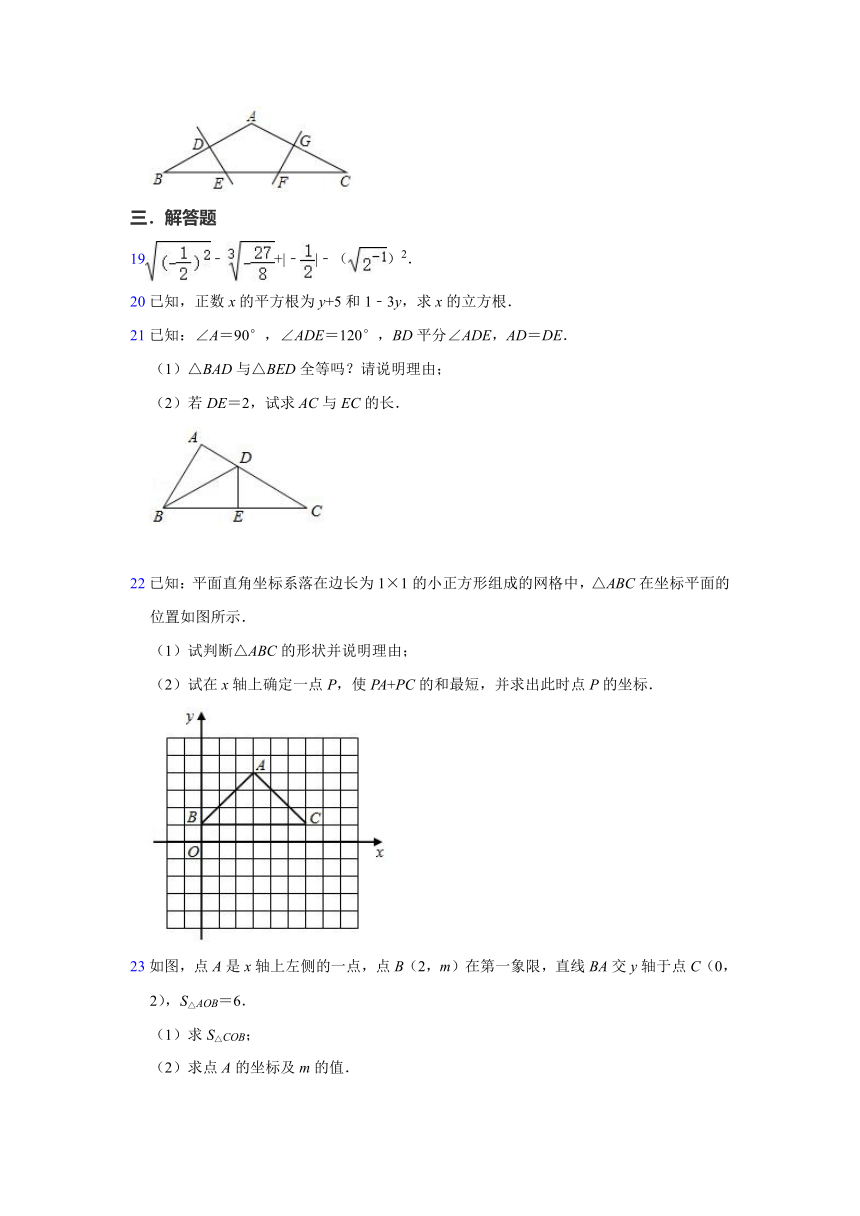
18如图,在△ABC中,AB=AC,∠A=120°,BC=18cm.AB的垂直平分线交AB于点D,交BC于点E;AC的垂直平分线交AC于点G,交BC于点F.EF的长为 .
三.解答题
19﹣+|﹣|﹣()2.
20已知,正数x的平方根为y+5和1﹣3y,求x的立方根.
21已知:∠A=90°,∠ADE=120°,BD平分∠ADE,AD=DE.
(1)△BAD与△BED全等吗?请说明理由;
(2)若DE=2,试求AC与EC的长.
22已知:平面直角坐标系落在边长为1×1的小正方形组成的网格中,△ABC在坐标平面的位置如图所示.
(1)试判断△ABC的形状并说明理由;
(2)试在x轴上确定一点P,使PA+PC的和最短,并求出此时点P的坐标.
23如图,点A是x轴上左侧的一点,点B(2,m)在第一象限,直线BA交y轴于点C(0,2),S△AOB=6.
(1)求S△COB;
(2)求点A的坐标及m的值.
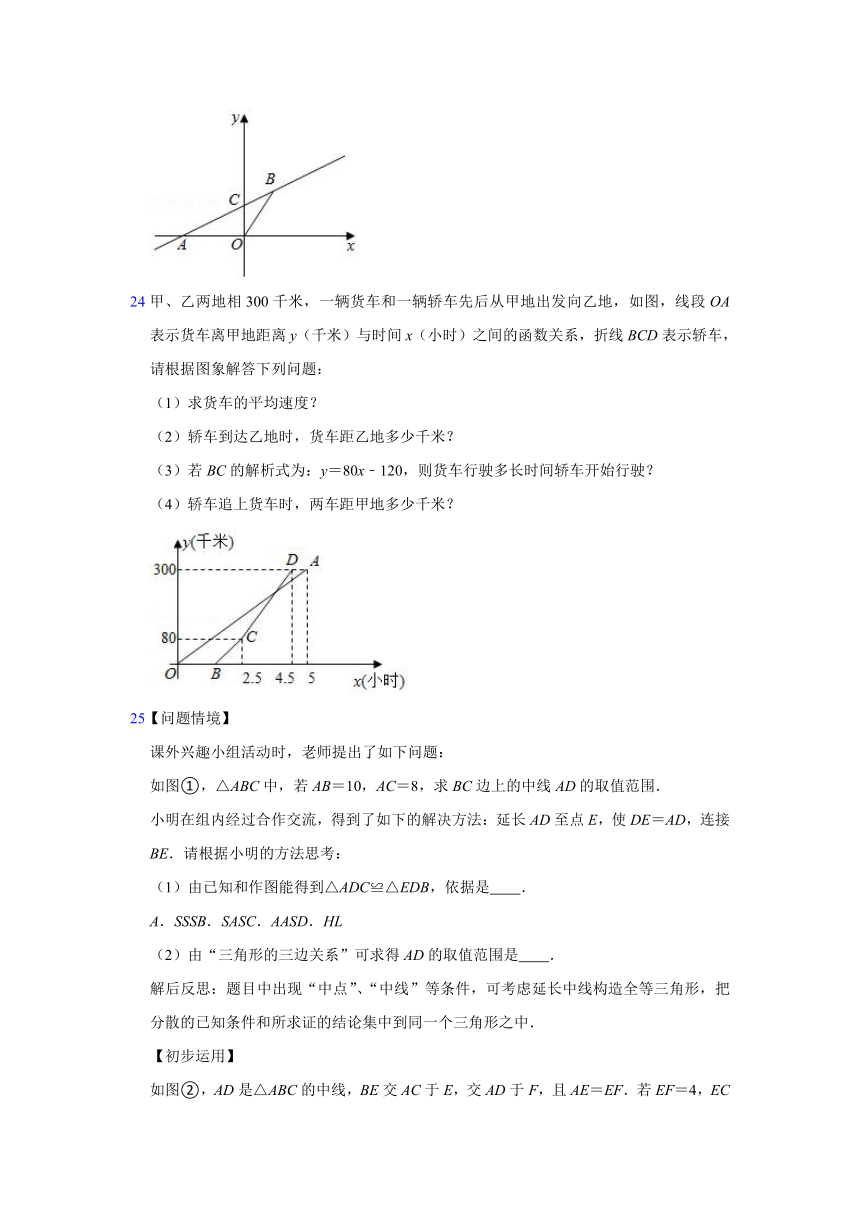
24甲、乙两地相300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系,折线BCD表示轿车,请根据图象解答下列问题:
(1)求货车的平均速度?
(2)轿车到达乙地时,货车距乙地多少千米?
(3)若BC的解析式为:y=80x﹣120,则货车行驶多长时间轿车开始行驶?
(4)轿车追上货车时,两车距甲地多少千米?
25【问题情境】
课外兴趣小组活动时,老师提出了如下问题:
如图①,△ABC中,若AB=10,AC=8,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB,依据是 .
A.SSSB.SASC.AASD.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】
如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=4,EC=3,求线段BF的长.
【灵活运用】
如图③,在△ABC中,∠A=90°,D为BC中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
参考答案与试题解析
一.选择题(共12小题)
1.下列说法正确的是( )
A.带根号的数都是无理数
B.无限小数都是无理数
C.两个无理数之和一定是无理数
D.两个无理数之积不一定是无理数
【分析】根据无理数是无限不循环小数,可得答案.
【解答】解:A、无理数是无限不循环小数,故A错误;
B、无理数是无限不循环小数,故B错误;
C、+(﹣)=0是有理数,故C错误;
D、×=2,故D正确;
故选:D.
2.下列各式正确的是( )
A.=﹣2
B.(﹣)2=
C.=﹣2
D.(﹣)3=﹣6
【分析】根据立方根,二次根式的性质,算术平方根分别求出每个式子的值,再得出选项即可.
【解答】解:A、结果是﹣2,故本选项正确;
B、结果是5,故本选项错误;
C、结果是2,故本选项错误;
D、结果是﹣6,故本选项错误;
故选:A.
3.已知点(﹣2,y1),(1,y2)都在一次函数y=kx﹣1(k<0)的图象上,则y1,y2的大小关系是( )
A.y1>y2
B.y1<y2
C.y1=y2
D.无法确定
【分析】先根据一次函数的解析式判断出函数的增减性,再根据两点横坐标的大小即可得出结论.
【解答】解:∵一次函数y=kx﹣1中,k<0,
∴y随x的增大而减小,
∵﹣2<1,
∴y1>y2.
故选:A.
4.如图,点D是△ABC内一点,∠D=105°,∠1=∠2,则∠ACB的度数为( )
A.65°
B.70°
C.75°
D.80°
【分析】根据三角形内角和定理得∠1+∠BCD=180°﹣∠D=75°,得出∠2+∠BCD=∠ACB.
【解答】解:∵∠D=105°,
∴∠1+∠BCD=180°﹣∠D=75°,
∵∠1=∠2,
∴∠2+∠BCD=∠ACB=75°.
故选:C.
5.函数y=2x+2的图象如图所示,下列说法正确的是( )
A.当x>0时,y>2
B.当x<0时,y<0
C.当x>0时,y>0
D.当x>﹣1时,y>2
【分析】根据题目中的函数解析式和一次函数的性质解答即可.
【解答】解:在y=2x+2中,令x=0时,y=2,
∴当x>0时,y>2,
故选:A.
6.通过估算比较下列两个数的大小,其中正确的是( )
A.<
B.﹣<
C.<
D.<24
【分析】先判断正负,再估计大小,比较即可.
【解答】解:∵=0.1>0,<0,
>.
故A错误.
∵<﹣3,=﹣3.
∴B正确.
∵()2=,()2=.
∵>.
故C错误.
<3.
∴<24.
故D错误.
故选:B.
7.AB⊥BC,EC⊥BC,AD⊥DE,AD=DE,AB=3,BC=8,则CE长为( )
A.4
B.5
C.8
D.10
【分析】由“AAS”可证△ADB≌△DEC,可得AB=DC=3,BD=CE,即可求解.
【解答】解:∵AB⊥BC,EC⊥BC,AD⊥DE,
∴∠B=∠C=∠ADE=90°,
∴∠A+∠ADB=90°=∠ADB+∠EDC,
∴∠A=∠EDC,
在△ADB和△DEC中,
,
∴△ADB≌△DEC(AAS),
∴AB=DC=3,BD=CE,
∴BD=CE=BC﹣DC=5,
故选:B.
8.如图,若OA=2,OA与x轴负半轴的夹角是30°,则点A关于x轴的对称点A′的坐标为( )
A.(﹣,1)
B.(﹣,﹣1)
C.(,1)
D.(﹣,1)
【分析】直接利用直角三角形的性质以及勾股定理得出各边长,再利用关于x轴对称点的性质得出答案.
【解答】解:如图所示:过点A作AB⊥x轴于点B,
∵AO=2,∠AOB=30°,
∴AB=1,
故BO==,
∴A(﹣,1),
故点A关于x轴的对称点A′的坐标为(﹣,﹣1).
故选:B.
9.AD是△ABC的中线,∠ADB=45°,把△ADB沿直线AD翻折,点B落在B′的位置,BC=2,则CB′的长为( )
A.
B.2
C.
D.2
【分析】根据翻转变换的性质得到BD=B′D,∠BDB′=90°,AD是△ABC的中线,BD=CD,利用直角三角形的勾股定理得出答案.
【解答】解:由翻转变换的得到BD=B′D,∠BDA=∠ADB′=45°,
∴∠BDB′=45°+45°=90°,
又∵AD是△ABC的中线,
∴BD=CD=BC=1,
∴BD=B′D=CD=1,
在Rt△B′DC中,由勾股定理得,
B′C==,
故选:A.
10.如图,在△ABC和△DEC中,已知AB=DE,∠A=∠D,还需添加一个条件才能使△ABC≌△DEC,不能添加的条件是( )
A.∠ECB=∠DCA
B.BC=EC
C.∠B=∠E
D.DC=AC
【分析】根据全等三角形的判定定理逐个判断即可.
【解答】解:A.∵∠ECB=∠DCA,
∴∠ECB+∠ACE=∠DCA+∠ACE,
即∠ACB=∠DCE,
在△ABC和△DEC中
,
∴△ABC≌△DEC(AAS),故本选项不符合题意;
B.根据BC=EC,AB=DE,∠A=∠D不能推出△ABC≌△DEC,故本选项符合题意;
C.符合全等三角形的判定定理ASA,能推出△ABC≌△DEC,故本选项不符合题意;
D.符合全等三角形的判定定理SAS,能推出△ABC≌△DEC,故本选项不符合题意;
故选:B.
11.点P(m+3,m﹣1)在x轴上,则点P的坐标为( )
A.(0,﹣4)
B.(﹣3,0)
C.(﹣3,1)
D.(4,0)
【分析】根据x轴上点的纵坐标等于零,可得答案.
【解答】解:由题意,得m﹣1=0,
解得m=1,
∴m+3=4,
∴点P的坐标为(4,0),
故选:D.
12.已知A,B两地相距400km,某人驾车从A地到B地,途中加油一次.已知油箱中剩余油量y(L)与行驶路程x(km)之间的关系如图所示,假设汽车每100km耗油量保持不变,以下说法错误的是( )
A.出发时油箱中有20L油
B.途中加油30L
C.该汽车每100km耗油7.5L
D.汽车到达B地时油箱中还剩油15L
【分析】(1)由函数图象可以直接得出出发时油箱中油的数量;
(2)由函数图象可以直接得出途中加油的数量;
(3)根据函数图象可得汽车前200km的耗油量,就可以该汽车每100km耗油的数量;
(4)根据函数图象可得汽车前200km的耗油量,可得加油后200km的耗油量,加油后的油量﹣加油后200km的耗油量就可以求出剩余油量.
【解答】解:A、由函数图象可以直接得出出发时油箱中有20L油,故正确,不符合题意;
B、由函数图象可以直接得出途中加油30﹣5=25(L).故错误,符合题意;
C、根据函数图象可得汽车前200km的耗油20﹣5=15(L).
∴该汽车每100km耗油7.5L,故正确,不符合题意;
D、根据函数图象可得汽车前200km的耗油20﹣5=15(L).
∵汽车每100km耗油量保持不变,
∴加油后200km的耗油量为15L.
∴汽车到达B地时油箱中还剩油30﹣15=15(L).故正确,不符合题意.
故选:B.
二.填空题(共5小题)
13.﹣27的立方根与的平方根的和是 0或﹣6 .
【分析】分别利用平方根、立方根的定义求解即可.解题注意=9,所以求的算术平方根就是求9的平方根.
【解答】解:∵﹣27的立方根是﹣3,的平方根是±3,
所以它们的和为0或﹣6.
故答案为:0或﹣6.
14.在平面直角坐标系中,将直线y=2x+6向右平移两个单位得到直线l,则直线l的表达式是 y=2x+2 .
【分析】直接根据“左加右减”的原则进行解答即可.
【解答】解:由“左加右减”的原则可知:将直线y=2x+6向右平移两个单位得到直线l,则直线l的表达式是y=2(x﹣2)+6,即y=2x+2.
故答案为y=2x+2.
15.已知点P的坐标为(1+a,2a﹣2),且点P到两坐标轴的距离相等,则a的值是 3或 .
【分析】根据到坐标轴的距离相等列出绝对值方程,然后求解即可.
【解答】解:∵点P(1+a,2a﹣2)到两坐标轴的距离相等,
∴|1+a|=|2a﹣2|,
∴1+a=2a﹣2或1+a=﹣(2a﹣2),
解得a=3或a=.
故答案为:3或.
16.如图,在3×2的正方形网格中,已有两个小正方形被涂黑,再将其余小正方形涂黑一个,使整个图案构成一个轴对称图形的涂法有 1 种.
【分析】利用轴对称图形的定义进而求出符合题意的图形即可.
【解答】解:如图所示:将图中小正方形(标号为1中)涂黑,能使整个图案构成一个轴对称图形.
故答案为:1.
17.将腰长分别是2和1的两个等腰直角三角板按如图所示摆放,则AA′= .
【分析】由等腰直角三角形的性质可得∠ACB=∠A'CB'=45°,AC=2,A'C=1,可得∠ACA'=90°,利用勾股定理可求解.
【解答】解:∵△ABC和△A'B'C是等腰直角三角形,
∴∠ACB=∠A'CB'=45°,AC=2,A'C=1,
∴∠ACA'=90°,
∴AA'===,
故答案为.
18如图,在△ABC中,AB=AC,∠A=120°,BC=18cm.AB的垂直平分线交AB于点D,交BC于点E;AC的垂直平分线交AC于点G,交BC于点F.EF的长为 .
【考点】线段垂直平分线的性质;等腰三角形的性质;含30度角的直角三角形.
【专题】等腰三角形与直角三角形;运算能力;推理能力.
【答案】6cm.
【分析】由垂直平分线的性质得出△BEA与△CFA是等腰三角形,再证明△EAF为等边三角形即可得出答案.
【解答】解:连接AE,AF,
∵AB的垂直平分线交AB于点D,交BC于点E;AC的垂直平分线交AC于点G,
∴BE=AE,CF=AF,
∴∠EAB=∠B,∠CAF=∠C,
∵∠BAC=120°,AB=AC,
∴∠B=∠C=30°,
∴∠BAE+∠CAF=60°,∠AEF=∠AFE=60°,
∴△AEF是等边三角形,
∴AE=AF=EF,
∴BE=EF=FC,
∵BC=18cm,
∴EF=6cm.
故答案为:6cm.
19﹣+|﹣|﹣()2.
【考点】实数的运算;负整数指数幂.
【专题】实数;运算能力.
【答案】2.
【分析】分别计算出各项,化简即可得出答案.
【解答】解:原式=﹣(﹣)+﹣
=2.
20已知,正数x的平方根为y+5和1﹣3y,求x的立方根.
【考点】平方根;立方根.
【专题】计算题;运算能力.
【答案】4.
【分析】根据平方根的概念即可求出y的值及x的值,即可得出答案.
【解答】解:根据题意可得,
y+5+1﹣3y=0,
解得y=3,则x=64,
64的立方根为4,
所以x的立方根为4.
21已知:∠A=90°,∠ADE=120°,BD平分∠ADE,AD=DE.
(1)△BAD与△BED全等吗?请说明理由;
(2)若DE=2,试求AC与EC的长.
【考点】全等三角形的判定与性质.
【专题】图形的全等;等腰三角形与直角三角形;推理能力.
【答案】(1)△BAD与△BED全等,理由见解析过程;
(2)AC=6,CE=2.
【分析】(1)由“SAS”可证△ADB≌△EDB;
(2)由全等三角形的性质可得∠A=∠DEB=90°,AD=DE=2,由直角三角形的性质可求解.
【解答】解:(1)△BAD与△BED全等,
理由如下:∵BD平分∠ADE,
∴∠ADB=∠BDE=60°,
在△ADB和△EDB中,
,
∴△ADB≌△EDB(SAS);
(2)∵△ADB≌△EDB,
∴∠A=∠DEB=90°,AD=DE=2,
∵∠CDE=∠ADC﹣∠ADE=180°﹣120°=60°,
∴∠C=30°,
∴CD=2DE=4,CE=DE=2,
∴AC=AD+CD=6.
22已知:平面直角坐标系落在边长为1×1的小正方形组成的网格中,△ABC在坐标平面的位置如图所示.
(1)试判断△ABC的形状并说明理由;
(2)试在x轴上确定一点P,使PA+PC的和最短,并求出此时点P的坐标.
【考点】坐标与图形性质;勾股定理;勾股定理的逆定理;轴对称﹣最短路线问题.
【专题】一次函数及其应用;等腰三角形与直角三角形;平移、旋转与对称;运算能力.
【答案】(1)△ABC是等腰三角形;
(2)P(,0).
【分析】(1)计算出BC、AC、AB长,再利用AB=AC判定△ABC的形状;
(2)作点C关于x轴的对称点C′,连接AC′交x轴于点P,直线AC′的解析式,可得点P坐标.
【解答】解:(1)△ABC是等腰三角形,
理由:∵A(3,4),B(0,1),C(6,1),
∴AB==3,BC=6,AC==3,
∴AB=AC,
∴△ABC是等腰三角形;
(2)点P即为所求.
∵C(6,1),A(3,4),C′(6,﹣1),
∴可以假设直线AC′的解析式为y=kx+b,则有,
解得,
∴直线AC′的解析式为y=﹣x+9,
令y=0,可得x=,
∴P(,0).
23如图,点A是x轴上左侧的一点,点B(2,m)在第一象限,直线BA交y轴于点C(0,2),S△AOB=6.
(1)求S△COB;
(2)求点A的坐标及m的值.
【考点】一次函数图象上点的坐标特征.
【专题】一次函数及其应用;三角形;运算能力;推理能力.
【答案】(1)S△COB=2;
(2)A点坐标为(﹣4,0);m=3.
【分析】(1)根据三角形面积公式求解;
(2)先计算出S△AOC=4,利用三角形面积公式得OA?2=4,解得OA=4,则A点坐标为(﹣4,0);再利用待定系数法求直线AC的解析式,然后把B(2,m)代入可求出m的值.
【解答】解:(1)∵点B(2,m),点C(0,2),
∴S△COB=×2×2=2;
(2)∵S△AOB=6,S△COB=2,
∴S△AOC=6﹣2=4,
∴OA?OC=4,即OA?2=4,解得OA=4,
∴A点坐标为(﹣4,0);
设直线AC的解析式为y=kx+b,
把A(﹣4,0)、C(0,2)代入得,
解得,
∴直线AC的解析式为y=x+2,
把B
(2,m)代入得m=1+2=3.
24甲、乙两地相300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系,折线BCD表示轿车,请根据图象解答下列问题:
(1)求货车的平均速度?
(2)轿车到达乙地时,货车距乙地多少千米?
(3)若BC的解析式为:y=80x﹣120,则货车行驶多长时间轿车开始行驶?
(4)轿车追上货车时,两车距甲地多少千米?
【考点】一次函数的应用.
【专题】一次函数及其应用;应用意识.
【答案】(1)60千米/小时;
(2)30千米;
(3)货车行驶1.5小时轿车开始行驶;
(4)234千米.
【分析】(1)根据图象可知货车5小时行驶300千米,由此求出货车的速度为60千米/时;
(2)根据图象得出货车出发后4.5小时轿车到达乙地,由此求出轿车到达乙地时,货车行驶的路程为270千米,而甲、乙两地相距300千米,则此时货车距乙地的路程为:300﹣270=30千米;
(3)令y=0,求出x的值即可;
(4)设CD段的函数解析式为y=kx+b,将C(2.5,80),D(4.5,300)两点的坐标代入,运用待定系数法求出CD段的函数解析式,由货车的平均速度得线段OA对应的函数解析式为y=60x,列出方程求出相遇时间即可解决问题.
【解答】解:(1)根据图象信息:货车的速度V货=300÷5=60(千米/小时).
答:货车的平均速度是60千米/小时;
(2)∵轿车到达乙地的时间为货车出发后4.5小时,
∴轿车到达乙地时,货车行驶的路程为:4.5×60=270(千米),
此时,货车距乙地的路程为:300﹣270=30(千米).
答:轿车到达乙地后,货车距乙地30千米;
(3)y=0时,80x﹣120=0,
解得:x=1.5,
答:货车行驶1.5小时轿车开始行驶;
(4)设CD段函数解析式为y=kx+b(k≠0)(2.5≤x≤4.5).
∵C(2.5,80),D(4.5,300)在其图象上,
∴,解得,
∴CD段函数解析式:y=110x﹣195(2.5≤x≤4.5).
线段OA对应的函数解析式为y=60x,
由题意得:110x﹣195=60x,解得:x=3.9,
3.9×60=234(千米),
答:轿车追上货车时,两车距甲地234千米.
25【问题情境】
课外兴趣小组活动时,老师提出了如下问题:
如图①,△ABC中,若AB=10,AC=8,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB,依据是 .
A.SSSB.SASC.AASD.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】
如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=4,EC=3,求线段BF的长.
【灵活运用】
如图③,在△ABC中,∠A=90°,D为BC中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
【考点】三角形综合题.
【专题】三角形.
【答案】见试题解答内容
【分析】(1)根据全等三角形的判定定理解答;
(2)根据三角形的三边关系计算;
【初步运用】延长AD到M,使AD=DM,连接BM,证明△ADC≌△MDB,根据全等三角形的性质解答;
【灵活运用】延长ED到点G,使DG=ED,连接GF,GC,证明△DBE≌△DCG,得到BE=CG,根据勾股定理解答.
【解答】解:(1)在△ADC和△EDB中,
,
∴△ADC≌△EDB(SAS),
故选:B;
(2)AB﹣BE<AE<AB+BE,
∴1<AD<9,
故答案为:1<AD<9;
【初步运用】
延长AD到M,使AD=DM,连接BM,如图②
∵AD是△ABC中线,
∴BD=DC,
∵在△ADC和△MDB中
,
∴△ADC≌△MDB(SAS),
∴BM=AC=7,∠CAD=∠M,
∵AE=EF,
∴∠CAD=∠AFE,
∵∠AFE=∠BFD,
∴∠BFD=∠CAD=∠M,
∴BF=BM=AC,
即AC=BF=7.
【灵活运用】
延长ED到N,使ED=DN,连接CN,连接FN如图③
∵D是BC中点,
∴BD=DC,
∵在△BDE和△CDN中
∴△BDE≌△CDN(SAS)
∴BE=CN,∠B=∠NCD,
∵DE⊥DF,ED=DN
∴EF=FN
∵∠A=90°
∴∠B+∠ACB=90°
∴∠NCD+∠ACB=90°,即∠FCN=90°
在Rt△FCN中,NC2+FC2=FN2
∴BE2+FC2=EF2
一.选择题
1.下列说法正确的是( )
A.带根号的数都是无理数
B.无限小数都是无理数
C.两个无理数之和一定是无理数
D.两个无理数之积不一定是无理数
2.下列各式正确的是( )
A.=﹣2
B.(﹣)2=
C.=﹣2
D.(﹣)3=﹣6
3.已知点(﹣2,y1),(1,y2)都在一次函数y=kx﹣1(k<0)的图象上,则y1,y2的大小关系是( )
A.y1>y2
B.y1<y2
C.y1=y2
D.无法确定
4.如图,点D是△ABC内一点,∠D=105°,∠1=∠2,则∠ACB的度数为( )
A.65°
B.70°
C.75°
D.80°
5.函数y=2x+2的图象如图所示,下列说法正确的是( )
A.当x>0时,y>2
B.当x<0时,y<0
C.当x>0时,y>0
D.当x>﹣1时,y>2
6.通过估算比较下列两个数的大小,其中正确的是( )
A.<
B.﹣<
C.<
D.<24
7.AB⊥BC,EC⊥BC,AD⊥DE,AD=DE,AB=3,BC=8,则CE长为( )
A.4
B.5
C.8
D.10
8.如图,若OA=2,OA与x轴负半轴的夹角是30°,则点A关于x轴的对称点A′的坐标为( )
A.(﹣,1)
B.(﹣,﹣1)
C.(,1)
D.(﹣,1)
9.AD是△ABC的中线,∠ADB=45°,把△ADB沿直线AD翻折,点B落在B′的位置,BC=2,则CB′的长为( )
A.
B.2
C.
D.2
10.如图,在△ABC和△DEC中,已知AB=DE,∠A=∠D,还需添加一个条件才能使△ABC≌△DEC,不能添加的条件是( )
A.∠ECB=∠DCA
B.BC=EC
C.∠B=∠E
D.DC=AC
11.点P(m+3,m﹣1)在x轴上,则点P的坐标为( )
A.(0,﹣4)
B.(﹣3,0)
C.(﹣3,1)
D.(4,0)
12.已知A,B两地相距400km,某人驾车从A地到B地,途中加油一次.已知油箱中剩余油量y(L)与行驶路程x(km)之间的关系如图所示,假设汽车每100km耗油量保持不变,以下说法错误的是( )
A.出发时油箱中有20L油
B.途中加油30L
C.该汽车每100km耗油7.5L
D.汽车到达B地时油箱中还剩油15L
二.填空题
13.﹣27的立方根与的平方根的和是
.
14.在平面直角坐标系中,将直线y=2x+6向右平移两个单位得到直线l,则直线l的表达式是
.
15.已知点P的坐标为(1+a,2a﹣2),且点P到两坐标轴的距离相等,则a的值是
.
16.如图,在3×2的正方形网格中,已有两个小正方形被涂黑,再将其余小正方形涂黑一个,使整个图案构成一个轴对称图形的涂法有
种.
17.将腰长分别是2和1的两个等腰直角三角板按如图所示摆放,则AA′=
.
18如图,在△ABC中,AB=AC,∠A=120°,BC=18cm.AB的垂直平分线交AB于点D,交BC于点E;AC的垂直平分线交AC于点G,交BC于点F.EF的长为 .
三.解答题
19﹣+|﹣|﹣()2.
20已知,正数x的平方根为y+5和1﹣3y,求x的立方根.
21已知:∠A=90°,∠ADE=120°,BD平分∠ADE,AD=DE.
(1)△BAD与△BED全等吗?请说明理由;
(2)若DE=2,试求AC与EC的长.
22已知:平面直角坐标系落在边长为1×1的小正方形组成的网格中,△ABC在坐标平面的位置如图所示.
(1)试判断△ABC的形状并说明理由;
(2)试在x轴上确定一点P,使PA+PC的和最短,并求出此时点P的坐标.
23如图,点A是x轴上左侧的一点,点B(2,m)在第一象限,直线BA交y轴于点C(0,2),S△AOB=6.
(1)求S△COB;
(2)求点A的坐标及m的值.
24甲、乙两地相300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系,折线BCD表示轿车,请根据图象解答下列问题:
(1)求货车的平均速度?
(2)轿车到达乙地时,货车距乙地多少千米?
(3)若BC的解析式为:y=80x﹣120,则货车行驶多长时间轿车开始行驶?
(4)轿车追上货车时,两车距甲地多少千米?
25【问题情境】
课外兴趣小组活动时,老师提出了如下问题:
如图①,△ABC中,若AB=10,AC=8,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB,依据是 .
A.SSSB.SASC.AASD.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】
如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=4,EC=3,求线段BF的长.
【灵活运用】
如图③,在△ABC中,∠A=90°,D为BC中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
参考答案与试题解析
一.选择题(共12小题)
1.下列说法正确的是( )
A.带根号的数都是无理数
B.无限小数都是无理数
C.两个无理数之和一定是无理数
D.两个无理数之积不一定是无理数
【分析】根据无理数是无限不循环小数,可得答案.
【解答】解:A、无理数是无限不循环小数,故A错误;
B、无理数是无限不循环小数,故B错误;
C、+(﹣)=0是有理数,故C错误;
D、×=2,故D正确;
故选:D.
2.下列各式正确的是( )
A.=﹣2
B.(﹣)2=
C.=﹣2
D.(﹣)3=﹣6
【分析】根据立方根,二次根式的性质,算术平方根分别求出每个式子的值,再得出选项即可.
【解答】解:A、结果是﹣2,故本选项正确;
B、结果是5,故本选项错误;
C、结果是2,故本选项错误;
D、结果是﹣6,故本选项错误;
故选:A.
3.已知点(﹣2,y1),(1,y2)都在一次函数y=kx﹣1(k<0)的图象上,则y1,y2的大小关系是( )
A.y1>y2
B.y1<y2
C.y1=y2
D.无法确定
【分析】先根据一次函数的解析式判断出函数的增减性,再根据两点横坐标的大小即可得出结论.
【解答】解:∵一次函数y=kx﹣1中,k<0,
∴y随x的增大而减小,
∵﹣2<1,
∴y1>y2.
故选:A.
4.如图,点D是△ABC内一点,∠D=105°,∠1=∠2,则∠ACB的度数为( )
A.65°
B.70°
C.75°
D.80°
【分析】根据三角形内角和定理得∠1+∠BCD=180°﹣∠D=75°,得出∠2+∠BCD=∠ACB.
【解答】解:∵∠D=105°,
∴∠1+∠BCD=180°﹣∠D=75°,
∵∠1=∠2,
∴∠2+∠BCD=∠ACB=75°.
故选:C.
5.函数y=2x+2的图象如图所示,下列说法正确的是( )
A.当x>0时,y>2
B.当x<0时,y<0
C.当x>0时,y>0
D.当x>﹣1时,y>2
【分析】根据题目中的函数解析式和一次函数的性质解答即可.
【解答】解:在y=2x+2中,令x=0时,y=2,
∴当x>0时,y>2,
故选:A.
6.通过估算比较下列两个数的大小,其中正确的是( )
A.<
B.﹣<
C.<
D.<24
【分析】先判断正负,再估计大小,比较即可.
【解答】解:∵=0.1>0,<0,
>.
故A错误.
∵<﹣3,=﹣3.
∴B正确.
∵()2=,()2=.
∵>.
故C错误.
<3.
∴<24.
故D错误.
故选:B.
7.AB⊥BC,EC⊥BC,AD⊥DE,AD=DE,AB=3,BC=8,则CE长为( )
A.4
B.5
C.8
D.10
【分析】由“AAS”可证△ADB≌△DEC,可得AB=DC=3,BD=CE,即可求解.
【解答】解:∵AB⊥BC,EC⊥BC,AD⊥DE,
∴∠B=∠C=∠ADE=90°,
∴∠A+∠ADB=90°=∠ADB+∠EDC,
∴∠A=∠EDC,
在△ADB和△DEC中,
,
∴△ADB≌△DEC(AAS),
∴AB=DC=3,BD=CE,
∴BD=CE=BC﹣DC=5,
故选:B.
8.如图,若OA=2,OA与x轴负半轴的夹角是30°,则点A关于x轴的对称点A′的坐标为( )
A.(﹣,1)
B.(﹣,﹣1)
C.(,1)
D.(﹣,1)
【分析】直接利用直角三角形的性质以及勾股定理得出各边长,再利用关于x轴对称点的性质得出答案.
【解答】解:如图所示:过点A作AB⊥x轴于点B,
∵AO=2,∠AOB=30°,
∴AB=1,
故BO==,
∴A(﹣,1),
故点A关于x轴的对称点A′的坐标为(﹣,﹣1).
故选:B.
9.AD是△ABC的中线,∠ADB=45°,把△ADB沿直线AD翻折,点B落在B′的位置,BC=2,则CB′的长为( )
A.
B.2
C.
D.2
【分析】根据翻转变换的性质得到BD=B′D,∠BDB′=90°,AD是△ABC的中线,BD=CD,利用直角三角形的勾股定理得出答案.
【解答】解:由翻转变换的得到BD=B′D,∠BDA=∠ADB′=45°,
∴∠BDB′=45°+45°=90°,
又∵AD是△ABC的中线,
∴BD=CD=BC=1,
∴BD=B′D=CD=1,
在Rt△B′DC中,由勾股定理得,
B′C==,
故选:A.
10.如图,在△ABC和△DEC中,已知AB=DE,∠A=∠D,还需添加一个条件才能使△ABC≌△DEC,不能添加的条件是( )
A.∠ECB=∠DCA
B.BC=EC
C.∠B=∠E
D.DC=AC
【分析】根据全等三角形的判定定理逐个判断即可.
【解答】解:A.∵∠ECB=∠DCA,
∴∠ECB+∠ACE=∠DCA+∠ACE,
即∠ACB=∠DCE,
在△ABC和△DEC中
,
∴△ABC≌△DEC(AAS),故本选项不符合题意;
B.根据BC=EC,AB=DE,∠A=∠D不能推出△ABC≌△DEC,故本选项符合题意;
C.符合全等三角形的判定定理ASA,能推出△ABC≌△DEC,故本选项不符合题意;
D.符合全等三角形的判定定理SAS,能推出△ABC≌△DEC,故本选项不符合题意;
故选:B.
11.点P(m+3,m﹣1)在x轴上,则点P的坐标为( )
A.(0,﹣4)
B.(﹣3,0)
C.(﹣3,1)
D.(4,0)
【分析】根据x轴上点的纵坐标等于零,可得答案.
【解答】解:由题意,得m﹣1=0,
解得m=1,
∴m+3=4,
∴点P的坐标为(4,0),
故选:D.
12.已知A,B两地相距400km,某人驾车从A地到B地,途中加油一次.已知油箱中剩余油量y(L)与行驶路程x(km)之间的关系如图所示,假设汽车每100km耗油量保持不变,以下说法错误的是( )
A.出发时油箱中有20L油
B.途中加油30L
C.该汽车每100km耗油7.5L
D.汽车到达B地时油箱中还剩油15L
【分析】(1)由函数图象可以直接得出出发时油箱中油的数量;
(2)由函数图象可以直接得出途中加油的数量;
(3)根据函数图象可得汽车前200km的耗油量,就可以该汽车每100km耗油的数量;
(4)根据函数图象可得汽车前200km的耗油量,可得加油后200km的耗油量,加油后的油量﹣加油后200km的耗油量就可以求出剩余油量.
【解答】解:A、由函数图象可以直接得出出发时油箱中有20L油,故正确,不符合题意;
B、由函数图象可以直接得出途中加油30﹣5=25(L).故错误,符合题意;
C、根据函数图象可得汽车前200km的耗油20﹣5=15(L).
∴该汽车每100km耗油7.5L,故正确,不符合题意;
D、根据函数图象可得汽车前200km的耗油20﹣5=15(L).
∵汽车每100km耗油量保持不变,
∴加油后200km的耗油量为15L.
∴汽车到达B地时油箱中还剩油30﹣15=15(L).故正确,不符合题意.
故选:B.
二.填空题(共5小题)
13.﹣27的立方根与的平方根的和是 0或﹣6 .
【分析】分别利用平方根、立方根的定义求解即可.解题注意=9,所以求的算术平方根就是求9的平方根.
【解答】解:∵﹣27的立方根是﹣3,的平方根是±3,
所以它们的和为0或﹣6.
故答案为:0或﹣6.
14.在平面直角坐标系中,将直线y=2x+6向右平移两个单位得到直线l,则直线l的表达式是 y=2x+2 .
【分析】直接根据“左加右减”的原则进行解答即可.
【解答】解:由“左加右减”的原则可知:将直线y=2x+6向右平移两个单位得到直线l,则直线l的表达式是y=2(x﹣2)+6,即y=2x+2.
故答案为y=2x+2.
15.已知点P的坐标为(1+a,2a﹣2),且点P到两坐标轴的距离相等,则a的值是 3或 .
【分析】根据到坐标轴的距离相等列出绝对值方程,然后求解即可.
【解答】解:∵点P(1+a,2a﹣2)到两坐标轴的距离相等,
∴|1+a|=|2a﹣2|,
∴1+a=2a﹣2或1+a=﹣(2a﹣2),
解得a=3或a=.
故答案为:3或.
16.如图,在3×2的正方形网格中,已有两个小正方形被涂黑,再将其余小正方形涂黑一个,使整个图案构成一个轴对称图形的涂法有 1 种.
【分析】利用轴对称图形的定义进而求出符合题意的图形即可.
【解答】解:如图所示:将图中小正方形(标号为1中)涂黑,能使整个图案构成一个轴对称图形.
故答案为:1.
17.将腰长分别是2和1的两个等腰直角三角板按如图所示摆放,则AA′= .
【分析】由等腰直角三角形的性质可得∠ACB=∠A'CB'=45°,AC=2,A'C=1,可得∠ACA'=90°,利用勾股定理可求解.
【解答】解:∵△ABC和△A'B'C是等腰直角三角形,
∴∠ACB=∠A'CB'=45°,AC=2,A'C=1,
∴∠ACA'=90°,
∴AA'===,
故答案为.
18如图,在△ABC中,AB=AC,∠A=120°,BC=18cm.AB的垂直平分线交AB于点D,交BC于点E;AC的垂直平分线交AC于点G,交BC于点F.EF的长为 .
【考点】线段垂直平分线的性质;等腰三角形的性质;含30度角的直角三角形.
【专题】等腰三角形与直角三角形;运算能力;推理能力.
【答案】6cm.
【分析】由垂直平分线的性质得出△BEA与△CFA是等腰三角形,再证明△EAF为等边三角形即可得出答案.
【解答】解:连接AE,AF,
∵AB的垂直平分线交AB于点D,交BC于点E;AC的垂直平分线交AC于点G,
∴BE=AE,CF=AF,
∴∠EAB=∠B,∠CAF=∠C,
∵∠BAC=120°,AB=AC,
∴∠B=∠C=30°,
∴∠BAE+∠CAF=60°,∠AEF=∠AFE=60°,
∴△AEF是等边三角形,
∴AE=AF=EF,
∴BE=EF=FC,
∵BC=18cm,
∴EF=6cm.
故答案为:6cm.
19﹣+|﹣|﹣()2.
【考点】实数的运算;负整数指数幂.
【专题】实数;运算能力.
【答案】2.
【分析】分别计算出各项,化简即可得出答案.
【解答】解:原式=﹣(﹣)+﹣
=2.
20已知,正数x的平方根为y+5和1﹣3y,求x的立方根.
【考点】平方根;立方根.
【专题】计算题;运算能力.
【答案】4.
【分析】根据平方根的概念即可求出y的值及x的值,即可得出答案.
【解答】解:根据题意可得,
y+5+1﹣3y=0,
解得y=3,则x=64,
64的立方根为4,
所以x的立方根为4.
21已知:∠A=90°,∠ADE=120°,BD平分∠ADE,AD=DE.
(1)△BAD与△BED全等吗?请说明理由;
(2)若DE=2,试求AC与EC的长.
【考点】全等三角形的判定与性质.
【专题】图形的全等;等腰三角形与直角三角形;推理能力.
【答案】(1)△BAD与△BED全等,理由见解析过程;
(2)AC=6,CE=2.
【分析】(1)由“SAS”可证△ADB≌△EDB;
(2)由全等三角形的性质可得∠A=∠DEB=90°,AD=DE=2,由直角三角形的性质可求解.
【解答】解:(1)△BAD与△BED全等,
理由如下:∵BD平分∠ADE,
∴∠ADB=∠BDE=60°,
在△ADB和△EDB中,
,
∴△ADB≌△EDB(SAS);
(2)∵△ADB≌△EDB,
∴∠A=∠DEB=90°,AD=DE=2,
∵∠CDE=∠ADC﹣∠ADE=180°﹣120°=60°,
∴∠C=30°,
∴CD=2DE=4,CE=DE=2,
∴AC=AD+CD=6.
22已知:平面直角坐标系落在边长为1×1的小正方形组成的网格中,△ABC在坐标平面的位置如图所示.
(1)试判断△ABC的形状并说明理由;
(2)试在x轴上确定一点P,使PA+PC的和最短,并求出此时点P的坐标.
【考点】坐标与图形性质;勾股定理;勾股定理的逆定理;轴对称﹣最短路线问题.
【专题】一次函数及其应用;等腰三角形与直角三角形;平移、旋转与对称;运算能力.
【答案】(1)△ABC是等腰三角形;
(2)P(,0).
【分析】(1)计算出BC、AC、AB长,再利用AB=AC判定△ABC的形状;
(2)作点C关于x轴的对称点C′,连接AC′交x轴于点P,直线AC′的解析式,可得点P坐标.
【解答】解:(1)△ABC是等腰三角形,
理由:∵A(3,4),B(0,1),C(6,1),
∴AB==3,BC=6,AC==3,
∴AB=AC,
∴△ABC是等腰三角形;
(2)点P即为所求.
∵C(6,1),A(3,4),C′(6,﹣1),
∴可以假设直线AC′的解析式为y=kx+b,则有,
解得,
∴直线AC′的解析式为y=﹣x+9,
令y=0,可得x=,
∴P(,0).
23如图,点A是x轴上左侧的一点,点B(2,m)在第一象限,直线BA交y轴于点C(0,2),S△AOB=6.
(1)求S△COB;
(2)求点A的坐标及m的值.
【考点】一次函数图象上点的坐标特征.
【专题】一次函数及其应用;三角形;运算能力;推理能力.
【答案】(1)S△COB=2;
(2)A点坐标为(﹣4,0);m=3.
【分析】(1)根据三角形面积公式求解;
(2)先计算出S△AOC=4,利用三角形面积公式得OA?2=4,解得OA=4,则A点坐标为(﹣4,0);再利用待定系数法求直线AC的解析式,然后把B(2,m)代入可求出m的值.
【解答】解:(1)∵点B(2,m),点C(0,2),
∴S△COB=×2×2=2;
(2)∵S△AOB=6,S△COB=2,
∴S△AOC=6﹣2=4,
∴OA?OC=4,即OA?2=4,解得OA=4,
∴A点坐标为(﹣4,0);
设直线AC的解析式为y=kx+b,
把A(﹣4,0)、C(0,2)代入得,
解得,
∴直线AC的解析式为y=x+2,
把B
(2,m)代入得m=1+2=3.
24甲、乙两地相300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系,折线BCD表示轿车,请根据图象解答下列问题:
(1)求货车的平均速度?
(2)轿车到达乙地时,货车距乙地多少千米?
(3)若BC的解析式为:y=80x﹣120,则货车行驶多长时间轿车开始行驶?
(4)轿车追上货车时,两车距甲地多少千米?
【考点】一次函数的应用.
【专题】一次函数及其应用;应用意识.
【答案】(1)60千米/小时;
(2)30千米;
(3)货车行驶1.5小时轿车开始行驶;
(4)234千米.
【分析】(1)根据图象可知货车5小时行驶300千米,由此求出货车的速度为60千米/时;
(2)根据图象得出货车出发后4.5小时轿车到达乙地,由此求出轿车到达乙地时,货车行驶的路程为270千米,而甲、乙两地相距300千米,则此时货车距乙地的路程为:300﹣270=30千米;
(3)令y=0,求出x的值即可;
(4)设CD段的函数解析式为y=kx+b,将C(2.5,80),D(4.5,300)两点的坐标代入,运用待定系数法求出CD段的函数解析式,由货车的平均速度得线段OA对应的函数解析式为y=60x,列出方程求出相遇时间即可解决问题.
【解答】解:(1)根据图象信息:货车的速度V货=300÷5=60(千米/小时).
答:货车的平均速度是60千米/小时;
(2)∵轿车到达乙地的时间为货车出发后4.5小时,
∴轿车到达乙地时,货车行驶的路程为:4.5×60=270(千米),
此时,货车距乙地的路程为:300﹣270=30(千米).
答:轿车到达乙地后,货车距乙地30千米;
(3)y=0时,80x﹣120=0,
解得:x=1.5,
答:货车行驶1.5小时轿车开始行驶;
(4)设CD段函数解析式为y=kx+b(k≠0)(2.5≤x≤4.5).
∵C(2.5,80),D(4.5,300)在其图象上,
∴,解得,
∴CD段函数解析式:y=110x﹣195(2.5≤x≤4.5).
线段OA对应的函数解析式为y=60x,
由题意得:110x﹣195=60x,解得:x=3.9,
3.9×60=234(千米),
答:轿车追上货车时,两车距甲地234千米.
25【问题情境】
课外兴趣小组活动时,老师提出了如下问题:
如图①,△ABC中,若AB=10,AC=8,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB,依据是 .
A.SSSB.SASC.AASD.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】
如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=4,EC=3,求线段BF的长.
【灵活运用】
如图③,在△ABC中,∠A=90°,D为BC中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
【考点】三角形综合题.
【专题】三角形.
【答案】见试题解答内容
【分析】(1)根据全等三角形的判定定理解答;
(2)根据三角形的三边关系计算;
【初步运用】延长AD到M,使AD=DM,连接BM,证明△ADC≌△MDB,根据全等三角形的性质解答;
【灵活运用】延长ED到点G,使DG=ED,连接GF,GC,证明△DBE≌△DCG,得到BE=CG,根据勾股定理解答.
【解答】解:(1)在△ADC和△EDB中,
,
∴△ADC≌△EDB(SAS),
故选:B;
(2)AB﹣BE<AE<AB+BE,
∴1<AD<9,
故答案为:1<AD<9;
【初步运用】
延长AD到M,使AD=DM,连接BM,如图②
∵AD是△ABC中线,
∴BD=DC,
∵在△ADC和△MDB中
,
∴△ADC≌△MDB(SAS),
∴BM=AC=7,∠CAD=∠M,
∵AE=EF,
∴∠CAD=∠AFE,
∵∠AFE=∠BFD,
∴∠BFD=∠CAD=∠M,
∴BF=BM=AC,
即AC=BF=7.
【灵活运用】
延长ED到N,使ED=DN,连接CN,连接FN如图③
∵D是BC中点,
∴BD=DC,
∵在△BDE和△CDN中
∴△BDE≌△CDN(SAS)
∴BE=CN,∠B=∠NCD,
∵DE⊥DF,ED=DN
∴EF=FN
∵∠A=90°
∴∠B+∠ACB=90°
∴∠NCD+∠ACB=90°,即∠FCN=90°
在Rt△FCN中,NC2+FC2=FN2
∴BE2+FC2=EF2
同课章节目录
