2020-2021学年山东省淄博市周村区六年级下学期期末数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2020-2021学年山东省淄博市周村区六年级下学期期末数学试卷(五四学制)(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 316.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 10:44:24 | ||
图片预览




文档简介
2020-2021学年山东省淄博市周村区六年级(下)期末数学试卷(五四学制)
一、选择题(在每小题给出的四个选项中,只有一个是正确的,请把正确的选项填在题后的括号内,每小题4分,共48分)
1.北斗卫星导航系统(BDS)是中国自行研制的全球卫星导航系统,未来在亚太地区定位精度将优于5米,测速精度优于0.1米/秒,授时精度优于10纳秒,10纳秒为0.00000001秒,0.00000001用科学记数法表示为( )
A.0.1×10﹣7
B.1×10﹣8
C.1×10﹣7
D.0.1×10﹣8
2.以下调查中,适宜抽样调查的是( )
A.了解某班学生的身高情况
B.掌握疫情期间某班学生体温情况
C.调查某批次汽车的抗撞击能力
D.选出某校短跑最快的学生参加全市比赛
3.下列运算正确的是( )
A.a2+a3=a5
B.(ab2)3=ab6
C.(﹣a2)3=a6
D.a2?a3=a5
4.如图,点P在直线l外,点A,B在直线l上,若PA=3.5,PB=6,则点P到直线l的距离可能是( )
A.3
B.4
C.5
D.6
5.将三角尺与直尺按如图所示摆放,∠α与∠β之间的关系一定正确的是( )
A.∠α=∠β
B.∠α=∠β
C.∠α+∠β=90°
D.∠α+∠β=180°
6.如图,直线AB,CD交于点O,射线OM平分∠AOC,如果∠AOD=104°,那么∠BOM等于( )
A.38°
B.104°
C.140°
D.142°
7.如图,下列条件:①∠DCA=∠CAF,②∠C=∠EDB,③∠BAC+∠C=180°,④∠GDE+∠B=180°.其中能判断AB∥CD的是( )
A.①④
B.②③④
C.①③④
D.①②③
8.长方形的周长为24cm,其中一边为xcm(其中x>0),面积为ycm2,则y与x的关系可以表示为( )
A.y=x2
B.y=(12﹣x)2
C.y=2(12﹣x)
D.y=x(12﹣x)
9.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x(kg)间有下面的关系:
x
0
1
2
3
4
5
y
10
10.5
11
11.5
12
12.5
下列说法一定错误的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂重物时的长度为0cm
C.物体质量x每增加1kg,弹簧长度y增加0.5cm
D.所挂物体质量为6kg时,弹簧长度为13cm
10.如图所示,货车匀速通过隧道(隧道长大于货车长)时,货车从进入隧道至离开隧道的时间x与货车在隧道内的长度y之间的关系用图象描述大致是( )
A.
B.
C.
D.
11.计算(﹣0.25)2021×(﹣4)2020的结果是( )
A.﹣
B.
C.﹣4
D.4
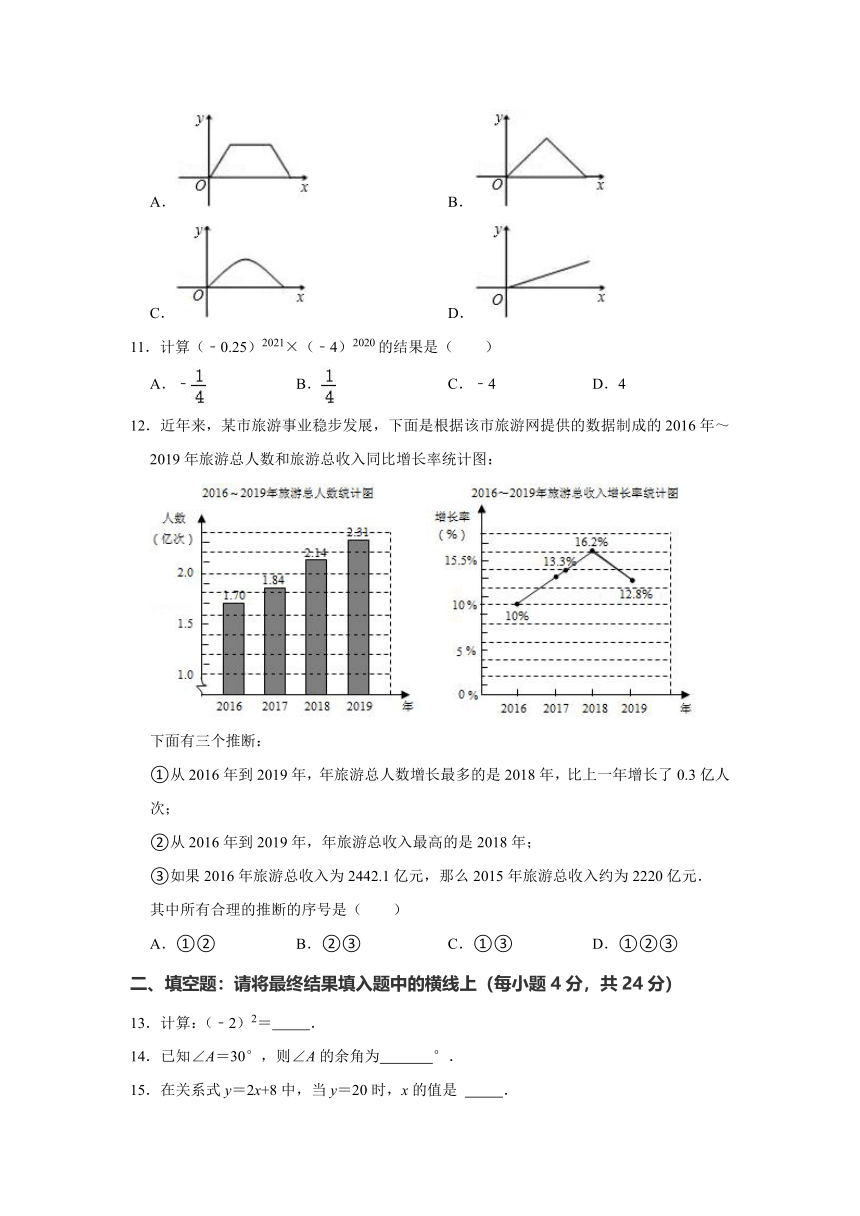
12.近年来,某市旅游事业稳步发展,下面是根据该市旅游网提供的数据制成的2016年~2019年旅游总人数和旅游总收入同比增长率统计图:
下面有三个推断:
①从2016年到2019年,年旅游总人数增长最多的是2018年,比上一年增长了0.3亿人次;
②从2016年到2019年,年旅游总收入最高的是2018年;
③如果2016年旅游总收入为2442.1亿元,那么2015年旅游总收入约为2220亿元.
其中所有合理的推断的序号是( )
A.①②
B.②③
C.①③
D.①②③
二、填空题:请将最终结果填入题中的横线上(每小题4分,共24分)
13.计算:(﹣2)2=
.
14.已知∠A=30°,则∠A的余角为
°.
15.在关系式y=2x+8中,当y=20时,x的值是
.
16.已知一组数据的最大值是256,最小值是200.画频数分布直方图时,若设定组距为6,则这组数据应分成
组.
17.如图,直线BC,DE相交于点O,AO⊥BC,OM平分∠BOD,如果∠AOE=50°,那么∠BOM的度数是
.
18.某城市自来水收费实行阶梯水价,收费标准如下表所示,用户5月份交水费45元,则所用水为
方.
月用水量
不超过12方部分
超过12方不超过18方部分
超过18方部分
收费标准(元/方)
2
2.5
3
三、解答题.解答要写出必要的文字说明或演算步骤.(共78分)
19.计算:
(1)(a+b)(a﹣b)﹣a2.
(2)(﹣3m)2(mn)3÷(﹣3m4n2).
20.已知2x2﹣2x=1,求代数式(x﹣1)2+(x﹣3)(x+3)的值.
21.声音在空气中传播的速度(简称音速)与气温之间的关系如下表:
气温/℃
5
10
15
20
音速/(m/s)
334
337
340
343
(1)这个表反映出的两个变量,
是自变量,
是因变量;
(2)从表中可以看出气温每升高5℃,音速就提高
m/s;可以估计当气温为0℃时,音速为
m/s;
(3)如果气温用x(℃)表示,音速用y(m/s)表示,请写出y与x之间的表达式,并求出当气温为40℃时,音速为多少?
22.已知:如图,C,D是直线AB上两点,FE∥DC,连接CE,DE,DF,DE平分∠CDF,且∠1+∠2=180°.
(1)请你猜想CE与DF的位置关系,并证明;
(2)若∠DCE=α,求∠DEF的大小(用含α的式子表示).
23.如图,AB∥CD,AF交BD于点F,∠CDE=∠BAF.
(1)求证:DE∥AF;
(2)若∠ABF=100°,∠ADB=50°,∠CDE=10°,求∠DAF的度数.
24.某电子品牌商下设台式电脑部、平板电脑部、手机部等.2018年的前五个月该品牌全部商品销售额共计600万元.下表表示该品牌商2018年前五个月的月销售额(统计信息不全).图1表示该品牌手机部各月销售额占该品牌所有商品当月销售额的百分比情况统计图.
品牌月销售额统计表(单位:万元)
月份
1月
2月
3月
4月
5月
品牌月销售额
180
90
115
95
(1)该品牌5月份的销售额是
万元;
(2)手机部5月份的销售额是
万元;
小明同学观察图1后认为,手机部5月份的销售额比手机部4月份的销售额减少了,你同意他的看法吗?请说明理由;
(3)该品牌手机部有A、B、C、D、E五个机型,图2表示在5月份手机部各机型销售额占5月份手机部销售额的百分比情况统计图.则5月份
机型的销售额最高,销售额最高的机型占5月份该品牌销售额的百分比是
.
25.“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
(1)赛跑的全程是多少米?
(2)乌龟每分钟爬多少米?
(3)乌龟用了多少分钟追上了正在睡觉的兔子?
(4)兔子醒来,以48千米/时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,兔子中间停下睡觉用了多少分钟?
26.如图,AB⊥AK,点A在直线MN上,AB、AK分别与直线EF交于点B、C,∠MAB+∠KCF=90°.
(1)求证:EF∥MN;
(2)如图2,∠NAB与∠ECK的角平分线交于点G,求∠G的度数;
(3)如图3,在∠MAB内作射线AQ,使∠MAQ=2∠QAB,以点C为端点作射线CP,交直线AQ于点T,当∠CTA=60°时,直接写出∠FCP与∠ACP的关系式.
参考答案与试题解析
一.选择题(共12小题)
1.北斗卫星导航系统(BDS)是中国自行研制的全球卫星导航系统,未来在亚太地区定位精度将优于5米,测速精度优于0.1米/秒,授时精度优于10纳秒,10纳秒为0.00000001秒,0.00000001用科学记数法表示为( )
A.0.1×10﹣7
B.1×10﹣8
C.1×10﹣7
D.0.1×10﹣8
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:0.00000001=1×10﹣8.
故选:B.
2.以下调查中,适宜抽样调查的是( )
A.了解某班学生的身高情况
B.掌握疫情期间某班学生体温情况
C.调查某批次汽车的抗撞击能力
D.选出某校短跑最快的学生参加全市比赛
【分析】根据抽样调查、全面调查的意义,结合具体的问题情境进行判断即可.
【解答】解:A.了解某班学生的身高情况,适合使用全面调查,因此选项A不符合题意;
B.掌握疫情期间某班学生体温情况,适合使用全面调查,因此选项B不符合题意;
C.调查某批次汽车的抗撞击能力,适合使用抽样调查,因此选项C符合题意;
D.选出某校短跑最快的学生参加全市比赛,适合使用全面调查,因此选项D不符合题意;
故选:C.
3.下列运算正确的是( )
A.a2+a3=a5
B.(ab2)3=ab6
C.(﹣a2)3=a6
D.a2?a3=a5
【分析】分别根据合并同类项法则,积的乘方运算法则以及同底数幂的乘法法则逐一判断即可.
【解答】解:A.a2与a3不是同类项,所以不能合并,故本选项不合题意;
B.(ab2)3=a3b6,故本选项不合题意;
C.(﹣a2)3=﹣a6,故本选项不合题意;
D.a2?a3=a5,故本选项符合题意.
故选:D.
4.如图,点P在直线l外,点A,B在直线l上,若PA=3.5,PB=6,则点P到直线l的距离可能是( )
A.3
B.4
C.5
D.6
【分析】根据垂线段最短判断即可.
【解答】解:因为垂线段最短,
∴点P到直线l的距离不大于3.5,
即点P到直线l的距离可能是3.
故选:A.
5.将三角尺与直尺按如图所示摆放,∠α与∠β之间的关系一定正确的是( )
A.∠α=∠β
B.∠α=∠β
C.∠α+∠β=90°
D.∠α+∠β=180°
【分析】利用平角性质和余角、补角解得角之间的关系.
【解答】解:∵直尺一边是平角为180°,三角尺的顶角为90°,
∴α+90°+β=180°,
∴α+β=90°
故选:C.
6.如图,直线AB,CD交于点O,射线OM平分∠AOC,如果∠AOD=104°,那么∠BOM等于( )
A.38°
B.104°
C.140°
D.142°
【分析】根据邻补角互补求出∠AOC的度数,再根据角平分线的定义求出∠AOM的度数,然后根据平角等于180°列式计算即可得解.
【解答】解:∵∠AOD=104°,
∴∠AOC=76°,
∵射线OM平分∠AOC,
∴∠AOM=∠AOC=×76°=38°,
∴∠BOM=180°﹣∠AOM=180°﹣38°=142°.
故选:D.
7.如图,下列条件:①∠DCA=∠CAF,②∠C=∠EDB,③∠BAC+∠C=180°,④∠GDE+∠B=180°.其中能判断AB∥CD的是( )
A.①④
B.②③④
C.①③④
D.①②③
【分析】直接利用平行线的判定方法分别判断得出答案.
【解答】解:①当∠DCA=∠CAF时,AB∥CD,符合题意;
②当∠C=∠EDB时,AC∥DB,不合题意;
③当∠BAC+∠C=180°时,AB∥CD,符合题意;
④当∠GDE+∠B=180°时,
又∵∠GDE+∠EDB=180°,
∴∠B=∠EDB,
∴AB∥CD,符合题意;
故选:C.
8.长方形的周长为24cm,其中一边为xcm(其中x>0),面积为ycm2,则y与x的关系可以表示为( )
A.y=x2
B.y=(12﹣x)2
C.y=2(12﹣x)
D.y=x(12﹣x)
【分析】由含有x的代数式表示长方形的另一条边的长,再根据面积公式得出答案.
【解答】解:长方形的周长为24cm,其中一边为xcm,则另一条边的长为(12﹣x)cm,
所以y=x(12﹣x),
故选:D.
9.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x(kg)间有下面的关系:
x
0
1
2
3
4
5
y
10
10.5
11
11.5
12
12.5
下列说法一定错误的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂重物时的长度为0cm
C.物体质量x每增加1kg,弹簧长度y增加0.5cm
D.所挂物体质量为6kg时,弹簧长度为13cm
【分析】根据变量与常量,函数的表示方法,结合表格中数据的变化规律逐项进行判断即可.
【解答】解:A.x与y都是变量,且x是自变量,y是因变量,是正确的,因此选项A不符合题意;
B.弹簧不挂重物时的长度,即当x=0时y的值,此时y=10cm,因此选项B
符合题意;
C.物体质量x每增加1kg,弹簧长度y增加0.5cm,是正确的,因此选项C不符合题意;
D.根据物体质量x每增加1kg,弹簧长度y增加0.5cm,可得出所挂物体质量为6kg时,弹簧长度为13cm,是正确的,因此选项D不符合题意;
故选:B.
10.如图所示,货车匀速通过隧道(隧道长大于货车长)时,货车从进入隧道至离开隧道的时间x与货车在隧道内的长度y之间的关系用图象描述大致是( )
A.
B.
C.
D.
【分析】先分析题意,把各个时间段内y与x之间的关系分析清楚,本题是分段函数,分为三段.
【解答】解:根据题意可知货车进入隧道的时间x与货车在隧道内的长度y之间的关系具体可描述为:
当货车开始进入时y逐渐变大,货车完全进入后一段时间内y不变,当货车开始出来时y逐渐变小,
∴反映到图象上应选A.
故选:A.
11.计算(﹣0.25)2021×(﹣4)2020的结果是( )
A.﹣
B.
C.﹣4
D.4
【分析】积的乘方,等于每个因式乘法的积,据此计算即可.
【解答】解:(﹣0.25)2021×42020
=(﹣0.25)2020×(﹣4)2020×(﹣0.25)
=(0.25×4)2020×(﹣0.25)
=12020×(﹣0.25)
=1×(﹣0.25)
=﹣0.25=﹣.
故选:A.
12.近年来,某市旅游事业稳步发展,下面是根据该市旅游网提供的数据制成的2016年~2019年旅游总人数和旅游总收入同比增长率统计图:
下面有三个推断:
①从2016年到2019年,年旅游总人数增长最多的是2018年,比上一年增长了0.3亿人次;
②从2016年到2019年,年旅游总收入最高的是2018年;
③如果2016年旅游总收入为2442.1亿元,那么2015年旅游总收入约为2220亿元.
其中所有合理的推断的序号是( )
A.①②
B.②③
C.①③
D.①②③
【分析】①由条形图,分别计算从2016年到2019年年旅游总人数增长量,再比较即可;
②由折线图可得:从2016年到2019年,年旅游总收入最高的是2019年;
③由2016年旅游总收入为2442.1亿元,增长率为10%,即可求得2015年旅游总收入.
【解答】解:①∵1.84﹣1.70=0.14,2.14﹣1.84=0.30,2.31﹣2.14=0.17,
而0.14<0.17<0.30,
∴从2016年到2019年,年旅游总人数增长最多的是2018年,比上一年增长了0.3亿人次,故本选项推断合理;
②由折线图可知,从2016年到2019年,旅游总收入同比增长率连年增加,所以年旅游总收入最高的是2019年,故本选项推断不合理;
③∵2016年旅游总收入为2442.1亿元,增长率为10%,
∴2442.1÷(1+10%)≈2220(亿元),
∴2015年旅游总收入约为2220亿元,故本选项推断合理.
故选:C.
二.填空题(共6小题)
13.计算:(﹣2)2= 4 .
【分析】根据有理数乘方的意义可得.
【解答】解:(﹣2)2=(﹣2)×(﹣2)=4.
14.已知∠A=30°,则∠A的余角为 60 °.
【分析】若两个角的和为90°,则这两个角互余,依此进行解答.
【解答】解:∵∠A=30°,
∴∠A的余角=90°﹣30°=60°.
故答案为:60.
15.在关系式y=2x+8中,当y=20时,x的值是
6 .
【分析】把y的值代入解析式,解一元一次方程即可.
【解答】解:把y=20代入y=2x+8中,
得:20=2x+8,
解得:x=6.
故答案是6.
16.已知一组数据的最大值是256,最小值是200.画频数分布直方图时,若设定组距为6,则这组数据应分成
10 组.
【分析】用极差除以组距,如果商是整数,组数=这个整数加1,如果商不是整数,用进一法,确定组数.
【解答】解:∵(256﹣200)÷6=56÷6≈9.3,
∴分成的组数是10组,
故答案为:10.
17.如图,直线BC,DE相交于点O,AO⊥BC,OM平分∠BOD,如果∠AOE=50°,那么∠BOM的度数是
20° .
【分析】由余角的定义求得∠EOC=40°,然后结合对顶角相等和角平分线的性质得到∠BOM的度数.
【解答】解:如图,
∵AO⊥BC于点O.
∴∠AOC=90°,
∵∠AOE=50°,
∴∠EOC=90°﹣50°=40°,
又∠BOD=∠EOC=40°,OM平分∠BOD,
∴∠BOM=∠BOD=20°.
故答案为:20°.
18.某城市自来水收费实行阶梯水价,收费标准如下表所示,用户5月份交水费45元,则所用水为 20 方.
月用水量
不超过12方部分
超过12方不超过18方部分
超过18方部分
收费标准(元/方)
2
2.5
3
【分析】根据题意可知:先判断出该用户用的水与18方的关系,再设用水x方,水费为y元,继而求得关系式为y=39+3(x﹣18);将y=45时,代入上式即可求得所用水的方数.
【解答】解:∵45>12×2+6×2.5=39,
∴用户5月份交水费45元可知5月用水超过了18方,
设用水x方,水费为y元,则关系式为y=39+3(x﹣18).
当y=45时,x=20,
即用水20方.
故答案为:20.
三.解答题(共8小题)
19.计算:
(1)(a+b)(a﹣b)﹣a2.
(2)(﹣3m)2(mn)3÷(﹣3m4n2).
【分析】(1)根据平方差公式去括号,再合并同类项可得;
(2)先算积的乘方,再利用单项式乘单项式法则,单项式除以单项式法则计算可得.
【解答】解:(1)(a+b)(a﹣b)﹣a2
=a2﹣b2﹣a2
=﹣b2.
(2)(﹣3m)2(mn)3÷(﹣3m4n2)
=9m2?m3n3÷(﹣3m4n2)
=9m5n3÷(﹣3m4n2)
=﹣3mn.
20.已知2x2﹣2x=1,求代数式(x﹣1)2+(x﹣3)(x+3)的值.
【分析】根据完全平方公式、平方差公式可以化简题目中的式子,然后将2x2﹣2x=1代入化简后的式子即可解答本题.
【解答】解:(x﹣1)2+(x﹣3)(x+3)
=x2﹣2x+1+x2﹣9
=2x2﹣2x﹣8,
∵2x2﹣2x=1,
∴原式=1﹣8=﹣7.
21.声音在空气中传播的速度(简称音速)与气温之间的关系如下表:
气温/℃
5
10
15
20
音速/(m/s)
334
337
340
343
(1)这个表反映出的两个变量, 气温 是自变量, 音速 是因变量;
(2)从表中可以看出气温每升高5℃,音速就提高
3 m/s;可以估计当气温为0℃时,音速为
331 m/s;
(3)如果气温用x(℃)表示,音速用y(m/s)表示,请写出y与x之间的表达式,并求出当气温为40℃时,音速为多少?
【分析】(1)观察表格可得;
(2)气温为5℃,音速为334m/s,气温升高5℃变为10℃,音速为337m/s,此时337﹣334=3m/s,据此可得,气温为0℃时则音速将由气温为5℃的334m/s减少3m/s,据此可得;
(3)从表格中的数据变化可以看出:y是x的一次函数,设y与x之间的表达式是y=kx+b(k≠0),利用待定系数法可得函数表达式,令x=40,即可求得音速.
【解答】解:(1)由表格可知,
这一变化过程中,自变量是气温,因变量是音速,
故答案为:气温,音速;
(2)从表格可以看出:
气温每升高5℃,音速就提高3m/s,
可以估计当气温为0℃时,音速为
331m/s,
故答案为:3m/s,331;
(3)从表格中的数据变化可以看出:y是x的一次函数,
设y与x之间的表达式是y=kx+b(k≠0),
把x=10,y=337和x=20,y=343代入得:
,
解得,
∴y=x+331,
当x=40时,y=×40+331=355.
22.已知:如图,C,D是直线AB上两点,FE∥DC,连接CE,DE,DF,DE平分∠CDF,且∠1+∠2=180°.
(1)请你猜想CE与DF的位置关系,并证明;
(2)若∠DCE=α,求∠DEF的大小(用含α的式子表示).
【分析】(1)由补角的性质可得∠2=∠ECD,可证EC∥DF;
(2)由补角的性质和角平分线的性质可得∠CDE=∠FDE=,由平行线的性质可求解.
【解答】解:(1)CE∥DF,
理由如下:∵∠1+∠2=180°,∠1+∠ECD=180°,
∴∠2=∠ECD,
∴EC∥DF;
(2)∵∠2=∠ECD=α,∠2+∠FDC=180°,
∴∠FDC=180°﹣α,
∵DE平分∠CDF,
∴∠CDE=∠FDE=,
∵EF∥DC,
∴∠DEF=∠EDC=.
23.如图,AB∥CD,AF交BD于点F,∠CDE=∠BAF.
(1)求证:DE∥AF;
(2)若∠ABF=100°,∠ADB=50°,∠CDE=10°,求∠DAF的度数.
【分析】(1)根据平行线的判定与性质即可完成证明;
(2)结合(1)的结论即可求出结果.
【解答】(1)证明:∵AB∥CD,
∴∠CDA=∠BAD,
∵∠CDE=∠BAF.
∴∠EDA=∠FAD,
∴DE∥AF;
(2)∵AB∥CD,∠ABF=100°,
∴∠CDB=180°﹣100°=80°,
∵∠ADB=50°,∠CDE=10°,
∴∠EDA=∠CDB﹣∠ADB﹣∠CDE=80°﹣50°﹣10°=20°,
∴∠FAD=20°.
则∠DAF的度数为20°.
24.某电子品牌商下设台式电脑部、平板电脑部、手机部等.2018年的前五个月该品牌全部商品销售额共计600万元.下表表示该品牌商2018年前五个月的月销售额(统计信息不全).图1表示该品牌手机部各月销售额占该品牌所有商品当月销售额的百分比情况统计图.
品牌月销售额统计表(单位:万元)
月份
1月
2月
3月
4月
5月
品牌月销售额
180
90
115
95
120
(1)该品牌5月份的销售额是 120 万元;
(2)手机部5月份的销售额是 36 万元;
小明同学观察图1后认为,手机部5月份的销售额比手机部4月份的销售额减少了,你同意他的看法吗?请说明理由;
(3)该品牌手机部有A、B、C、D、E五个机型,图2表示在5月份手机部各机型销售额占5月份手机部销售额的百分比情况统计图.则5月份
机型的销售额最高,销售额最高的机型占5月份该品牌销售额的百分比是 8.4% .
【分析】(1)销售总额减去前4个月的销售额即可得;
(2)5月份销售额乘以手机所占百分比可得,计算出手机部4月份销售额,比较大小即可得;
(3)由扇形统计图各手机销售额所占百分比即可得.
【解答】解:(1)该品牌5月份的销售额是600﹣(180+90+115+95)=120(万元),
故答案为:120;
(2)不同意小明的看法,
手机部4月份销售额为:95×32%=30.4(万元).
手机部5月份销售额为:120×30%=36(万元).
因为36万元>30.4万元,
故小明说法错误,
故答案为:36.
(3)由扇形统计图知,5月份B机型的销售额最高,销售额最高的机型占5月份该品牌销售额的百分比是×100%=8.4%,
故答案为:B、8.4%.
25.“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
(1)赛跑的全程是多少米?
(2)乌龟每分钟爬多少米?
(3)乌龟用了多少分钟追上了正在睡觉的兔子?
(4)兔子醒来,以48千米/时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,兔子中间停下睡觉用了多少分钟?
【分析】(1)观察图象可得;
(2)由图象可知,线段OD表示乌龟的路程与时间的关系,时间为30分钟时路程为1500米,根据速度=路程÷时间可得;
(3)由图象可知,兔子睡觉时的路程为700米,根据时间=路程÷乌龟速度可得;
(4)用乌龟跑完全程的时间+兔子晚到的时间﹣兔子在路上奔跑的时间可得.
【解答】解:(1)由图象可知:
赛跑的全程为1500米;
(2)由图象可得:
乌龟每分钟爬1500÷30=50(米);
(3)700÷50=14(分钟)
∴乌龟用了14分钟追上了正在睡觉的兔子;
(4)48千米/时=800米/分,
30+0.5﹣1﹣(1500﹣700)÷800=28.5(分钟),
∴兔子中间停下睡觉用了28.5分钟.
26.如图,AB⊥AK,点A在直线MN上,AB、AK分别与直线EF交于点B、C,∠MAB+∠KCF=90°.
(1)求证:EF∥MN;
(2)如图2,∠NAB与∠ECK的角平分线交于点G,求∠G的度数;
(3)如图3,在∠MAB内作射线AQ,使∠MAQ=2∠QAB,以点C为端点作射线CP,交直线AQ于点T,当∠CTA=60°时,直接写出∠FCP与∠ACP的关系式.
【分析】(1)想办法证明∠KCF=∠CAN即可.
(2)设∠GCK=∠GCB=x,∠GAC=y,则∠GAD=∠GAN=90°﹣y,求出x﹣y的值,可得结论.
(3)分两种情形:)如图3﹣1中,当点T在QA的延长线上时,如图3﹣2中,当点T在AQ上时,分别求解即可.
【解答】(1)证明:如图1中,
∵AB⊥AK,
∴∠BAC=90°,
∴∠MAB+∠CAN=90°,
∵∠MAB+∠KCF=90°,
∴∠CAN=∠KCF,
∴EF∥MN.
(2)解:如图2中,
∵∠NAB与∠ECK的角平分线交于点G,
∴可以假设∠GCK=∠GCB=x,∠GAC=y,则∠GAD=∠GAN=90°﹣y,
∴∠CAN=90°﹣2y,
∵EF∥MN,
∴∠KCF=∠CAN=90°﹣2y,
∴90°﹣2y+2x=180°,
∴x﹣y=45°,
∵∠G=∠GCK﹣∠GAC=x﹣y,
∴∠G=45°.
(3)如图3﹣1中,当点T在QA的延长线上时,设∠QAB=x,则∠MAQ=2x,设MN交CP于J.
∵EF∥MN,
∴∠FCP=∠AJC=∠TAJ+∠ATC=2x+60°,
∴∠ACP=180°﹣60°﹣2x﹣(90°﹣3x)=30°+x,
∴∠FCP=2∠ACP,
如图3﹣2中,当点T在AQ上时,设∠QAB=x,则∠MAQ=2x,
∵∠ACP=180°﹣60°﹣(90°+x)=30°﹣x,
∴∠FCP=∠ACP+∠ACF=30°﹣x+(180°﹣90°﹣3x)=120°﹣4x,
∴∠ACF=90°+3x,∠FCP=∠ACP+∠ACF=30°﹣x+90°+3x=120°+2x,
∴∠FCP+2∠ACP=180°.
综上所述,∠FCP=2∠ACP或∠FCP+2∠ACP=180°.
一、选择题(在每小题给出的四个选项中,只有一个是正确的,请把正确的选项填在题后的括号内,每小题4分,共48分)
1.北斗卫星导航系统(BDS)是中国自行研制的全球卫星导航系统,未来在亚太地区定位精度将优于5米,测速精度优于0.1米/秒,授时精度优于10纳秒,10纳秒为0.00000001秒,0.00000001用科学记数法表示为( )
A.0.1×10﹣7
B.1×10﹣8
C.1×10﹣7
D.0.1×10﹣8
2.以下调查中,适宜抽样调查的是( )
A.了解某班学生的身高情况
B.掌握疫情期间某班学生体温情况
C.调查某批次汽车的抗撞击能力
D.选出某校短跑最快的学生参加全市比赛
3.下列运算正确的是( )
A.a2+a3=a5
B.(ab2)3=ab6
C.(﹣a2)3=a6
D.a2?a3=a5
4.如图,点P在直线l外,点A,B在直线l上,若PA=3.5,PB=6,则点P到直线l的距离可能是( )
A.3
B.4
C.5
D.6
5.将三角尺与直尺按如图所示摆放,∠α与∠β之间的关系一定正确的是( )
A.∠α=∠β
B.∠α=∠β
C.∠α+∠β=90°
D.∠α+∠β=180°
6.如图,直线AB,CD交于点O,射线OM平分∠AOC,如果∠AOD=104°,那么∠BOM等于( )
A.38°
B.104°
C.140°
D.142°
7.如图,下列条件:①∠DCA=∠CAF,②∠C=∠EDB,③∠BAC+∠C=180°,④∠GDE+∠B=180°.其中能判断AB∥CD的是( )
A.①④
B.②③④
C.①③④
D.①②③
8.长方形的周长为24cm,其中一边为xcm(其中x>0),面积为ycm2,则y与x的关系可以表示为( )
A.y=x2
B.y=(12﹣x)2
C.y=2(12﹣x)
D.y=x(12﹣x)
9.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x(kg)间有下面的关系:
x
0
1
2
3
4
5
y
10
10.5
11
11.5
12
12.5
下列说法一定错误的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂重物时的长度为0cm
C.物体质量x每增加1kg,弹簧长度y增加0.5cm
D.所挂物体质量为6kg时,弹簧长度为13cm
10.如图所示,货车匀速通过隧道(隧道长大于货车长)时,货车从进入隧道至离开隧道的时间x与货车在隧道内的长度y之间的关系用图象描述大致是( )
A.
B.
C.
D.
11.计算(﹣0.25)2021×(﹣4)2020的结果是( )
A.﹣
B.
C.﹣4
D.4
12.近年来,某市旅游事业稳步发展,下面是根据该市旅游网提供的数据制成的2016年~2019年旅游总人数和旅游总收入同比增长率统计图:
下面有三个推断:
①从2016年到2019年,年旅游总人数增长最多的是2018年,比上一年增长了0.3亿人次;
②从2016年到2019年,年旅游总收入最高的是2018年;
③如果2016年旅游总收入为2442.1亿元,那么2015年旅游总收入约为2220亿元.
其中所有合理的推断的序号是( )
A.①②
B.②③
C.①③
D.①②③
二、填空题:请将最终结果填入题中的横线上(每小题4分,共24分)
13.计算:(﹣2)2=
.
14.已知∠A=30°,则∠A的余角为
°.
15.在关系式y=2x+8中,当y=20时,x的值是
.
16.已知一组数据的最大值是256,最小值是200.画频数分布直方图时,若设定组距为6,则这组数据应分成
组.
17.如图,直线BC,DE相交于点O,AO⊥BC,OM平分∠BOD,如果∠AOE=50°,那么∠BOM的度数是
.
18.某城市自来水收费实行阶梯水价,收费标准如下表所示,用户5月份交水费45元,则所用水为
方.
月用水量
不超过12方部分
超过12方不超过18方部分
超过18方部分
收费标准(元/方)
2
2.5
3
三、解答题.解答要写出必要的文字说明或演算步骤.(共78分)
19.计算:
(1)(a+b)(a﹣b)﹣a2.
(2)(﹣3m)2(mn)3÷(﹣3m4n2).
20.已知2x2﹣2x=1,求代数式(x﹣1)2+(x﹣3)(x+3)的值.
21.声音在空气中传播的速度(简称音速)与气温之间的关系如下表:
气温/℃
5
10
15
20
音速/(m/s)
334
337
340
343
(1)这个表反映出的两个变量,
是自变量,
是因变量;
(2)从表中可以看出气温每升高5℃,音速就提高
m/s;可以估计当气温为0℃时,音速为
m/s;
(3)如果气温用x(℃)表示,音速用y(m/s)表示,请写出y与x之间的表达式,并求出当气温为40℃时,音速为多少?
22.已知:如图,C,D是直线AB上两点,FE∥DC,连接CE,DE,DF,DE平分∠CDF,且∠1+∠2=180°.
(1)请你猜想CE与DF的位置关系,并证明;
(2)若∠DCE=α,求∠DEF的大小(用含α的式子表示).
23.如图,AB∥CD,AF交BD于点F,∠CDE=∠BAF.
(1)求证:DE∥AF;
(2)若∠ABF=100°,∠ADB=50°,∠CDE=10°,求∠DAF的度数.
24.某电子品牌商下设台式电脑部、平板电脑部、手机部等.2018年的前五个月该品牌全部商品销售额共计600万元.下表表示该品牌商2018年前五个月的月销售额(统计信息不全).图1表示该品牌手机部各月销售额占该品牌所有商品当月销售额的百分比情况统计图.
品牌月销售额统计表(单位:万元)
月份
1月
2月
3月
4月
5月
品牌月销售额
180
90
115
95
(1)该品牌5月份的销售额是
万元;
(2)手机部5月份的销售额是
万元;
小明同学观察图1后认为,手机部5月份的销售额比手机部4月份的销售额减少了,你同意他的看法吗?请说明理由;
(3)该品牌手机部有A、B、C、D、E五个机型,图2表示在5月份手机部各机型销售额占5月份手机部销售额的百分比情况统计图.则5月份
机型的销售额最高,销售额最高的机型占5月份该品牌销售额的百分比是
.
25.“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
(1)赛跑的全程是多少米?
(2)乌龟每分钟爬多少米?
(3)乌龟用了多少分钟追上了正在睡觉的兔子?
(4)兔子醒来,以48千米/时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,兔子中间停下睡觉用了多少分钟?
26.如图,AB⊥AK,点A在直线MN上,AB、AK分别与直线EF交于点B、C,∠MAB+∠KCF=90°.
(1)求证:EF∥MN;
(2)如图2,∠NAB与∠ECK的角平分线交于点G,求∠G的度数;
(3)如图3,在∠MAB内作射线AQ,使∠MAQ=2∠QAB,以点C为端点作射线CP,交直线AQ于点T,当∠CTA=60°时,直接写出∠FCP与∠ACP的关系式.
参考答案与试题解析
一.选择题(共12小题)
1.北斗卫星导航系统(BDS)是中国自行研制的全球卫星导航系统,未来在亚太地区定位精度将优于5米,测速精度优于0.1米/秒,授时精度优于10纳秒,10纳秒为0.00000001秒,0.00000001用科学记数法表示为( )
A.0.1×10﹣7
B.1×10﹣8
C.1×10﹣7
D.0.1×10﹣8
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:0.00000001=1×10﹣8.
故选:B.
2.以下调查中,适宜抽样调查的是( )
A.了解某班学生的身高情况
B.掌握疫情期间某班学生体温情况
C.调查某批次汽车的抗撞击能力
D.选出某校短跑最快的学生参加全市比赛
【分析】根据抽样调查、全面调查的意义,结合具体的问题情境进行判断即可.
【解答】解:A.了解某班学生的身高情况,适合使用全面调查,因此选项A不符合题意;
B.掌握疫情期间某班学生体温情况,适合使用全面调查,因此选项B不符合题意;
C.调查某批次汽车的抗撞击能力,适合使用抽样调查,因此选项C符合题意;
D.选出某校短跑最快的学生参加全市比赛,适合使用全面调查,因此选项D不符合题意;
故选:C.
3.下列运算正确的是( )
A.a2+a3=a5
B.(ab2)3=ab6
C.(﹣a2)3=a6
D.a2?a3=a5
【分析】分别根据合并同类项法则,积的乘方运算法则以及同底数幂的乘法法则逐一判断即可.
【解答】解:A.a2与a3不是同类项,所以不能合并,故本选项不合题意;
B.(ab2)3=a3b6,故本选项不合题意;
C.(﹣a2)3=﹣a6,故本选项不合题意;
D.a2?a3=a5,故本选项符合题意.
故选:D.
4.如图,点P在直线l外,点A,B在直线l上,若PA=3.5,PB=6,则点P到直线l的距离可能是( )
A.3
B.4
C.5
D.6
【分析】根据垂线段最短判断即可.
【解答】解:因为垂线段最短,
∴点P到直线l的距离不大于3.5,
即点P到直线l的距离可能是3.
故选:A.
5.将三角尺与直尺按如图所示摆放,∠α与∠β之间的关系一定正确的是( )
A.∠α=∠β
B.∠α=∠β
C.∠α+∠β=90°
D.∠α+∠β=180°
【分析】利用平角性质和余角、补角解得角之间的关系.
【解答】解:∵直尺一边是平角为180°,三角尺的顶角为90°,
∴α+90°+β=180°,
∴α+β=90°
故选:C.
6.如图,直线AB,CD交于点O,射线OM平分∠AOC,如果∠AOD=104°,那么∠BOM等于( )
A.38°
B.104°
C.140°
D.142°
【分析】根据邻补角互补求出∠AOC的度数,再根据角平分线的定义求出∠AOM的度数,然后根据平角等于180°列式计算即可得解.
【解答】解:∵∠AOD=104°,
∴∠AOC=76°,
∵射线OM平分∠AOC,
∴∠AOM=∠AOC=×76°=38°,
∴∠BOM=180°﹣∠AOM=180°﹣38°=142°.
故选:D.
7.如图,下列条件:①∠DCA=∠CAF,②∠C=∠EDB,③∠BAC+∠C=180°,④∠GDE+∠B=180°.其中能判断AB∥CD的是( )
A.①④
B.②③④
C.①③④
D.①②③
【分析】直接利用平行线的判定方法分别判断得出答案.
【解答】解:①当∠DCA=∠CAF时,AB∥CD,符合题意;
②当∠C=∠EDB时,AC∥DB,不合题意;
③当∠BAC+∠C=180°时,AB∥CD,符合题意;
④当∠GDE+∠B=180°时,
又∵∠GDE+∠EDB=180°,
∴∠B=∠EDB,
∴AB∥CD,符合题意;
故选:C.
8.长方形的周长为24cm,其中一边为xcm(其中x>0),面积为ycm2,则y与x的关系可以表示为( )
A.y=x2
B.y=(12﹣x)2
C.y=2(12﹣x)
D.y=x(12﹣x)
【分析】由含有x的代数式表示长方形的另一条边的长,再根据面积公式得出答案.
【解答】解:长方形的周长为24cm,其中一边为xcm,则另一条边的长为(12﹣x)cm,
所以y=x(12﹣x),
故选:D.
9.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x(kg)间有下面的关系:
x
0
1
2
3
4
5
y
10
10.5
11
11.5
12
12.5
下列说法一定错误的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂重物时的长度为0cm
C.物体质量x每增加1kg,弹簧长度y增加0.5cm
D.所挂物体质量为6kg时,弹簧长度为13cm
【分析】根据变量与常量,函数的表示方法,结合表格中数据的变化规律逐项进行判断即可.
【解答】解:A.x与y都是变量,且x是自变量,y是因变量,是正确的,因此选项A不符合题意;
B.弹簧不挂重物时的长度,即当x=0时y的值,此时y=10cm,因此选项B
符合题意;
C.物体质量x每增加1kg,弹簧长度y增加0.5cm,是正确的,因此选项C不符合题意;
D.根据物体质量x每增加1kg,弹簧长度y增加0.5cm,可得出所挂物体质量为6kg时,弹簧长度为13cm,是正确的,因此选项D不符合题意;
故选:B.
10.如图所示,货车匀速通过隧道(隧道长大于货车长)时,货车从进入隧道至离开隧道的时间x与货车在隧道内的长度y之间的关系用图象描述大致是( )
A.
B.
C.
D.
【分析】先分析题意,把各个时间段内y与x之间的关系分析清楚,本题是分段函数,分为三段.
【解答】解:根据题意可知货车进入隧道的时间x与货车在隧道内的长度y之间的关系具体可描述为:
当货车开始进入时y逐渐变大,货车完全进入后一段时间内y不变,当货车开始出来时y逐渐变小,
∴反映到图象上应选A.
故选:A.
11.计算(﹣0.25)2021×(﹣4)2020的结果是( )
A.﹣
B.
C.﹣4
D.4
【分析】积的乘方,等于每个因式乘法的积,据此计算即可.
【解答】解:(﹣0.25)2021×42020
=(﹣0.25)2020×(﹣4)2020×(﹣0.25)
=(0.25×4)2020×(﹣0.25)
=12020×(﹣0.25)
=1×(﹣0.25)
=﹣0.25=﹣.
故选:A.
12.近年来,某市旅游事业稳步发展,下面是根据该市旅游网提供的数据制成的2016年~2019年旅游总人数和旅游总收入同比增长率统计图:
下面有三个推断:
①从2016年到2019年,年旅游总人数增长最多的是2018年,比上一年增长了0.3亿人次;
②从2016年到2019年,年旅游总收入最高的是2018年;
③如果2016年旅游总收入为2442.1亿元,那么2015年旅游总收入约为2220亿元.
其中所有合理的推断的序号是( )
A.①②
B.②③
C.①③
D.①②③
【分析】①由条形图,分别计算从2016年到2019年年旅游总人数增长量,再比较即可;
②由折线图可得:从2016年到2019年,年旅游总收入最高的是2019年;
③由2016年旅游总收入为2442.1亿元,增长率为10%,即可求得2015年旅游总收入.
【解答】解:①∵1.84﹣1.70=0.14,2.14﹣1.84=0.30,2.31﹣2.14=0.17,
而0.14<0.17<0.30,
∴从2016年到2019年,年旅游总人数增长最多的是2018年,比上一年增长了0.3亿人次,故本选项推断合理;
②由折线图可知,从2016年到2019年,旅游总收入同比增长率连年增加,所以年旅游总收入最高的是2019年,故本选项推断不合理;
③∵2016年旅游总收入为2442.1亿元,增长率为10%,
∴2442.1÷(1+10%)≈2220(亿元),
∴2015年旅游总收入约为2220亿元,故本选项推断合理.
故选:C.
二.填空题(共6小题)
13.计算:(﹣2)2= 4 .
【分析】根据有理数乘方的意义可得.
【解答】解:(﹣2)2=(﹣2)×(﹣2)=4.
14.已知∠A=30°,则∠A的余角为 60 °.
【分析】若两个角的和为90°,则这两个角互余,依此进行解答.
【解答】解:∵∠A=30°,
∴∠A的余角=90°﹣30°=60°.
故答案为:60.
15.在关系式y=2x+8中,当y=20时,x的值是
6 .
【分析】把y的值代入解析式,解一元一次方程即可.
【解答】解:把y=20代入y=2x+8中,
得:20=2x+8,
解得:x=6.
故答案是6.
16.已知一组数据的最大值是256,最小值是200.画频数分布直方图时,若设定组距为6,则这组数据应分成
10 组.
【分析】用极差除以组距,如果商是整数,组数=这个整数加1,如果商不是整数,用进一法,确定组数.
【解答】解:∵(256﹣200)÷6=56÷6≈9.3,
∴分成的组数是10组,
故答案为:10.
17.如图,直线BC,DE相交于点O,AO⊥BC,OM平分∠BOD,如果∠AOE=50°,那么∠BOM的度数是
20° .
【分析】由余角的定义求得∠EOC=40°,然后结合对顶角相等和角平分线的性质得到∠BOM的度数.
【解答】解:如图,
∵AO⊥BC于点O.
∴∠AOC=90°,
∵∠AOE=50°,
∴∠EOC=90°﹣50°=40°,
又∠BOD=∠EOC=40°,OM平分∠BOD,
∴∠BOM=∠BOD=20°.
故答案为:20°.
18.某城市自来水收费实行阶梯水价,收费标准如下表所示,用户5月份交水费45元,则所用水为 20 方.
月用水量
不超过12方部分
超过12方不超过18方部分
超过18方部分
收费标准(元/方)
2
2.5
3
【分析】根据题意可知:先判断出该用户用的水与18方的关系,再设用水x方,水费为y元,继而求得关系式为y=39+3(x﹣18);将y=45时,代入上式即可求得所用水的方数.
【解答】解:∵45>12×2+6×2.5=39,
∴用户5月份交水费45元可知5月用水超过了18方,
设用水x方,水费为y元,则关系式为y=39+3(x﹣18).
当y=45时,x=20,
即用水20方.
故答案为:20.
三.解答题(共8小题)
19.计算:
(1)(a+b)(a﹣b)﹣a2.
(2)(﹣3m)2(mn)3÷(﹣3m4n2).
【分析】(1)根据平方差公式去括号,再合并同类项可得;
(2)先算积的乘方,再利用单项式乘单项式法则,单项式除以单项式法则计算可得.
【解答】解:(1)(a+b)(a﹣b)﹣a2
=a2﹣b2﹣a2
=﹣b2.
(2)(﹣3m)2(mn)3÷(﹣3m4n2)
=9m2?m3n3÷(﹣3m4n2)
=9m5n3÷(﹣3m4n2)
=﹣3mn.
20.已知2x2﹣2x=1,求代数式(x﹣1)2+(x﹣3)(x+3)的值.
【分析】根据完全平方公式、平方差公式可以化简题目中的式子,然后将2x2﹣2x=1代入化简后的式子即可解答本题.
【解答】解:(x﹣1)2+(x﹣3)(x+3)
=x2﹣2x+1+x2﹣9
=2x2﹣2x﹣8,
∵2x2﹣2x=1,
∴原式=1﹣8=﹣7.
21.声音在空气中传播的速度(简称音速)与气温之间的关系如下表:
气温/℃
5
10
15
20
音速/(m/s)
334
337
340
343
(1)这个表反映出的两个变量, 气温 是自变量, 音速 是因变量;
(2)从表中可以看出气温每升高5℃,音速就提高
3 m/s;可以估计当气温为0℃时,音速为
331 m/s;
(3)如果气温用x(℃)表示,音速用y(m/s)表示,请写出y与x之间的表达式,并求出当气温为40℃时,音速为多少?
【分析】(1)观察表格可得;
(2)气温为5℃,音速为334m/s,气温升高5℃变为10℃,音速为337m/s,此时337﹣334=3m/s,据此可得,气温为0℃时则音速将由气温为5℃的334m/s减少3m/s,据此可得;
(3)从表格中的数据变化可以看出:y是x的一次函数,设y与x之间的表达式是y=kx+b(k≠0),利用待定系数法可得函数表达式,令x=40,即可求得音速.
【解答】解:(1)由表格可知,
这一变化过程中,自变量是气温,因变量是音速,
故答案为:气温,音速;
(2)从表格可以看出:
气温每升高5℃,音速就提高3m/s,
可以估计当气温为0℃时,音速为
331m/s,
故答案为:3m/s,331;
(3)从表格中的数据变化可以看出:y是x的一次函数,
设y与x之间的表达式是y=kx+b(k≠0),
把x=10,y=337和x=20,y=343代入得:
,
解得,
∴y=x+331,
当x=40时,y=×40+331=355.
22.已知:如图,C,D是直线AB上两点,FE∥DC,连接CE,DE,DF,DE平分∠CDF,且∠1+∠2=180°.
(1)请你猜想CE与DF的位置关系,并证明;
(2)若∠DCE=α,求∠DEF的大小(用含α的式子表示).
【分析】(1)由补角的性质可得∠2=∠ECD,可证EC∥DF;
(2)由补角的性质和角平分线的性质可得∠CDE=∠FDE=,由平行线的性质可求解.
【解答】解:(1)CE∥DF,
理由如下:∵∠1+∠2=180°,∠1+∠ECD=180°,
∴∠2=∠ECD,
∴EC∥DF;
(2)∵∠2=∠ECD=α,∠2+∠FDC=180°,
∴∠FDC=180°﹣α,
∵DE平分∠CDF,
∴∠CDE=∠FDE=,
∵EF∥DC,
∴∠DEF=∠EDC=.
23.如图,AB∥CD,AF交BD于点F,∠CDE=∠BAF.
(1)求证:DE∥AF;
(2)若∠ABF=100°,∠ADB=50°,∠CDE=10°,求∠DAF的度数.
【分析】(1)根据平行线的判定与性质即可完成证明;
(2)结合(1)的结论即可求出结果.
【解答】(1)证明:∵AB∥CD,
∴∠CDA=∠BAD,
∵∠CDE=∠BAF.
∴∠EDA=∠FAD,
∴DE∥AF;
(2)∵AB∥CD,∠ABF=100°,
∴∠CDB=180°﹣100°=80°,
∵∠ADB=50°,∠CDE=10°,
∴∠EDA=∠CDB﹣∠ADB﹣∠CDE=80°﹣50°﹣10°=20°,
∴∠FAD=20°.
则∠DAF的度数为20°.
24.某电子品牌商下设台式电脑部、平板电脑部、手机部等.2018年的前五个月该品牌全部商品销售额共计600万元.下表表示该品牌商2018年前五个月的月销售额(统计信息不全).图1表示该品牌手机部各月销售额占该品牌所有商品当月销售额的百分比情况统计图.
品牌月销售额统计表(单位:万元)
月份
1月
2月
3月
4月
5月
品牌月销售额
180
90
115
95
120
(1)该品牌5月份的销售额是 120 万元;
(2)手机部5月份的销售额是 36 万元;
小明同学观察图1后认为,手机部5月份的销售额比手机部4月份的销售额减少了,你同意他的看法吗?请说明理由;
(3)该品牌手机部有A、B、C、D、E五个机型,图2表示在5月份手机部各机型销售额占5月份手机部销售额的百分比情况统计图.则5月份
机型的销售额最高,销售额最高的机型占5月份该品牌销售额的百分比是 8.4% .
【分析】(1)销售总额减去前4个月的销售额即可得;
(2)5月份销售额乘以手机所占百分比可得,计算出手机部4月份销售额,比较大小即可得;
(3)由扇形统计图各手机销售额所占百分比即可得.
【解答】解:(1)该品牌5月份的销售额是600﹣(180+90+115+95)=120(万元),
故答案为:120;
(2)不同意小明的看法,
手机部4月份销售额为:95×32%=30.4(万元).
手机部5月份销售额为:120×30%=36(万元).
因为36万元>30.4万元,
故小明说法错误,
故答案为:36.
(3)由扇形统计图知,5月份B机型的销售额最高,销售额最高的机型占5月份该品牌销售额的百分比是×100%=8.4%,
故答案为:B、8.4%.
25.“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
(1)赛跑的全程是多少米?
(2)乌龟每分钟爬多少米?
(3)乌龟用了多少分钟追上了正在睡觉的兔子?
(4)兔子醒来,以48千米/时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,兔子中间停下睡觉用了多少分钟?
【分析】(1)观察图象可得;
(2)由图象可知,线段OD表示乌龟的路程与时间的关系,时间为30分钟时路程为1500米,根据速度=路程÷时间可得;
(3)由图象可知,兔子睡觉时的路程为700米,根据时间=路程÷乌龟速度可得;
(4)用乌龟跑完全程的时间+兔子晚到的时间﹣兔子在路上奔跑的时间可得.
【解答】解:(1)由图象可知:
赛跑的全程为1500米;
(2)由图象可得:
乌龟每分钟爬1500÷30=50(米);
(3)700÷50=14(分钟)
∴乌龟用了14分钟追上了正在睡觉的兔子;
(4)48千米/时=800米/分,
30+0.5﹣1﹣(1500﹣700)÷800=28.5(分钟),
∴兔子中间停下睡觉用了28.5分钟.
26.如图,AB⊥AK,点A在直线MN上,AB、AK分别与直线EF交于点B、C,∠MAB+∠KCF=90°.
(1)求证:EF∥MN;
(2)如图2,∠NAB与∠ECK的角平分线交于点G,求∠G的度数;
(3)如图3,在∠MAB内作射线AQ,使∠MAQ=2∠QAB,以点C为端点作射线CP,交直线AQ于点T,当∠CTA=60°时,直接写出∠FCP与∠ACP的关系式.
【分析】(1)想办法证明∠KCF=∠CAN即可.
(2)设∠GCK=∠GCB=x,∠GAC=y,则∠GAD=∠GAN=90°﹣y,求出x﹣y的值,可得结论.
(3)分两种情形:)如图3﹣1中,当点T在QA的延长线上时,如图3﹣2中,当点T在AQ上时,分别求解即可.
【解答】(1)证明:如图1中,
∵AB⊥AK,
∴∠BAC=90°,
∴∠MAB+∠CAN=90°,
∵∠MAB+∠KCF=90°,
∴∠CAN=∠KCF,
∴EF∥MN.
(2)解:如图2中,
∵∠NAB与∠ECK的角平分线交于点G,
∴可以假设∠GCK=∠GCB=x,∠GAC=y,则∠GAD=∠GAN=90°﹣y,
∴∠CAN=90°﹣2y,
∵EF∥MN,
∴∠KCF=∠CAN=90°﹣2y,
∴90°﹣2y+2x=180°,
∴x﹣y=45°,
∵∠G=∠GCK﹣∠GAC=x﹣y,
∴∠G=45°.
(3)如图3﹣1中,当点T在QA的延长线上时,设∠QAB=x,则∠MAQ=2x,设MN交CP于J.
∵EF∥MN,
∴∠FCP=∠AJC=∠TAJ+∠ATC=2x+60°,
∴∠ACP=180°﹣60°﹣2x﹣(90°﹣3x)=30°+x,
∴∠FCP=2∠ACP,
如图3﹣2中,当点T在AQ上时,设∠QAB=x,则∠MAQ=2x,
∵∠ACP=180°﹣60°﹣(90°+x)=30°﹣x,
∴∠FCP=∠ACP+∠ACF=30°﹣x+(180°﹣90°﹣3x)=120°﹣4x,
∴∠ACF=90°+3x,∠FCP=∠ACP+∠ACF=30°﹣x+90°+3x=120°+2x,
∴∠FCP+2∠ACP=180°.
综上所述,∠FCP=2∠ACP或∠FCP+2∠ACP=180°.
同课章节目录
