湖南省怀化市新晃县2019-2020学年九年级下学期数学期末考试试卷(Word版 含解析)
文档属性
| 名称 | 湖南省怀化市新晃县2019-2020学年九年级下学期数学期末考试试卷(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 267.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 11:15:13 | ||
图片预览



文档简介
2019-2020学年下学期湖南省新晃县九年级数学期末考试试卷
一.选择题
1.方程2x2=4的解是( )
A.
B.2
C.
D.±2
2.若cos30°?sinα=,则锐角α等于( )
A.15°
B.30°
C.45°
D.60°
3.下列函数中,图象是双曲线且经过点(2,﹣4)的是( )
A.y=﹣2x
B.y=﹣
C.y=﹣
D.y=x﹣6
4.若x=1是方程x2+mx+3=0的一个根,则方程的另一个根是( )
A.3
B.4
C.﹣3
D.﹣4
5.用配方法解方程x2﹣4x﹣7=0,可变形为( )
A.(x+2)2=3
B.(x+2)2=11
C.(x﹣2)2=11
D.(x﹣2)2=3
6.已知△ABC∽△A1B1C1,且∠A=50°,∠B=95°,则∠C1等于( )
A.50°
B.95°
C.35°
D.25°
7.当太阳光线与水平地面成30°角时,一棵树的影长为24m,则该树高为( )
A.8m
B.4m
C.12m
D.12m
8.如图,在△ABC中,DE是它的中位线,BC=2,有下面三个结论:①DE=1;②△ADE∽△ABC;③△ADE的面积与△ABC的面积之比为1:4.其中正确结论的个数有( )
A.0个
B.1个
C.2个
D.3个
9.某学校在开展“节约每一滴水”的活动中,从九年级的180名同学中任选出10名同学汇报了各自家庭一个月的节水情况,将有关数据整理成下表:
节水量/t
0.5
1
1.5
2
人数
2
3
4
1
请你估计这180名同学的家庭一个月节约用水的总量大约是( )
A.180t
B.200t
C.216t
D.360t
10.关于x的一元二次方程(k+1)x2+4x﹣1=0有实数根,则k的取值范围是( )
A.k>﹣5
B.k>﹣5且k≠﹣1
C.k≥﹣5
D.k≥﹣5且k≠﹣1
二.填空题
11.若,则=
.
12.函数y=中,若x>2,则y的取值范围为
.
13.设x1,x2分别为一元二次方程x2+2019x+1=0的两个实数根,则x1x2﹣x1﹣x2=
.
14.如图所示,增加一个条件,可使△ABC∽△AED,这个条件可以是
.
15.将一块长8cm、宽6cm的矩形铁皮的四个角各截去一个面积相同的小正方形,做成一个无盖的盒子,要使盒子的底面积是原来铁皮的面积的,若设盒子的高为xcm,则列出的方程为
.
16.若反比例函数y=(a是常数)的图象的同一支上有两点(x1,y1),(x2,y2),设b=(x1﹣x2)(y1﹣y2),则一次函数y=bx﹣b的图象不经过第
象限.
三.解答题
17解一元二次方程:
(1)x2﹣4x﹣12=0;
(2)(2x﹣1)2=3(2x﹣1).
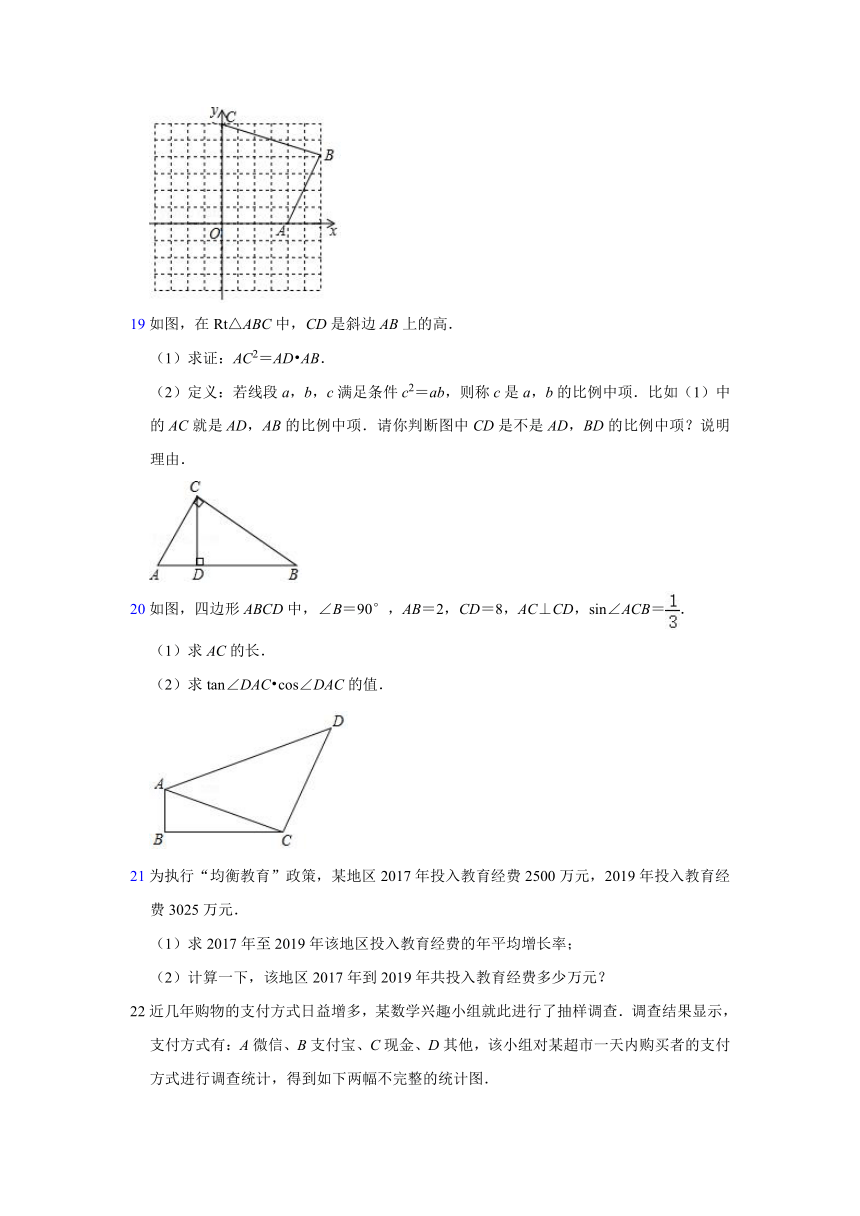
18在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(4,0),B(6,4),C(0,6),将其顶点的坐标缩小为原来的,画出得到的四边形.并判断这两个四边形是位似图形吗?若是,位似比是多少?
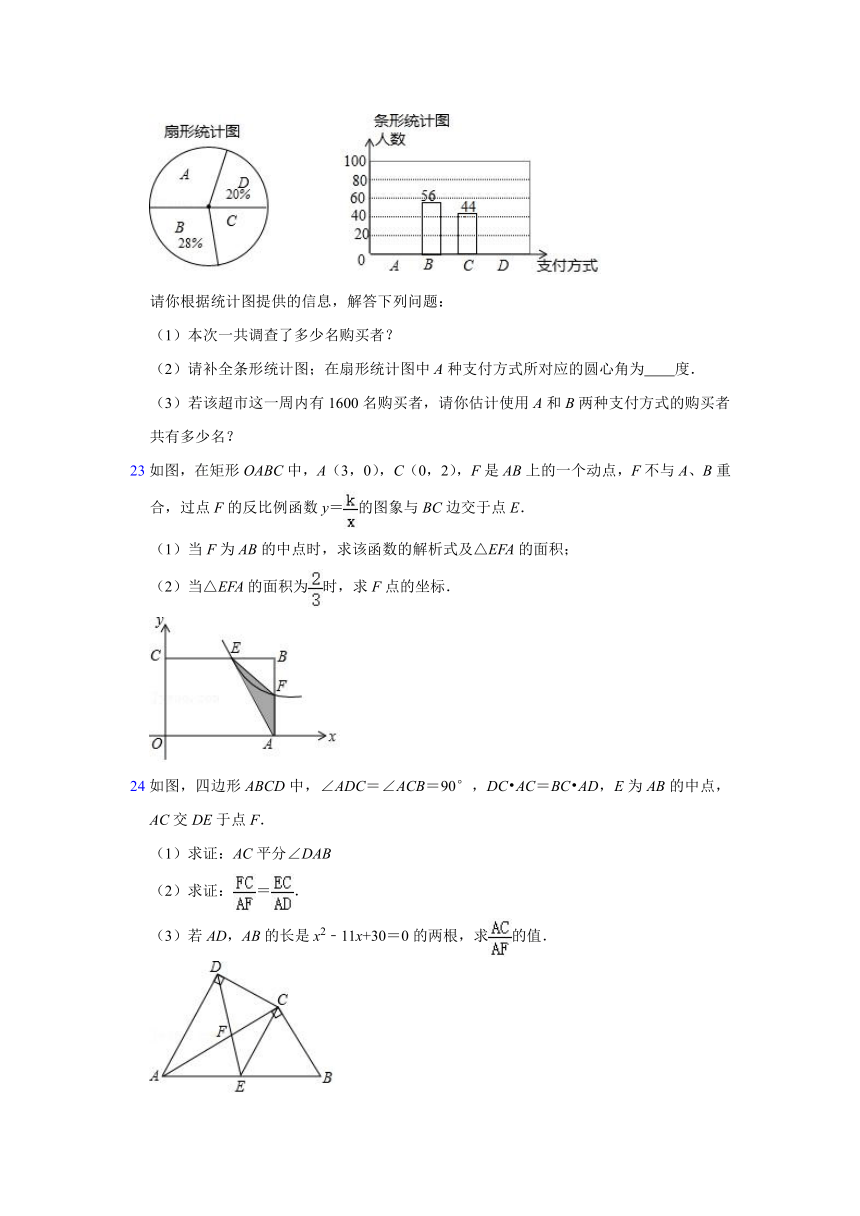
19如图,在Rt△ABC中,CD是斜边AB上的高.
(1)求证:AC2=AD?AB.
(2)定义:若线段a,b,c满足条件c2=ab,则称c是a,b的比例中项.比如(1)中的AC就是AD,AB的比例中项.请你判断图中CD是不是AD,BD的比例中项?说明理由.
20如图,四边形ABCD中,∠B=90°,AB=2,CD=8,AC⊥CD,sin∠ACB=.
(1)求AC的长.
(2)求tan∠DAC?cos∠DAC的值.
21为执行“均衡教育”政策,某地区2017年投入教育经费2500万元,2019年投入教育经费3025万元.
(1)求2017年至2019年该地区投入教育经费的年平均增长率;
(2)计算一下,该地区2017年到2019年共投入教育经费多少万元?
22近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
23如图,在矩形OABC中,A(3,0),C(0,2),F是AB上的一个动点,F不与A、B重合,过点F的反比例函数y=的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式及△EFA的面积;
(2)当△EFA的面积为时,求F点的坐标.
24如图,四边形ABCD中,∠ADC=∠ACB=90°,DC?AC=BC?AD,E为AB的中点,AC交DE于点F.
(1)求证:AC平分∠DAB
(2)求证:=.
(3)若AD,AB的长是x2﹣11x+30=0的两根,求的值.
参考答案与试题解析
一.选择题(共10小题)
1.方程2x2=4的解是( )
A.
B.2
C.
D.±2
【分析】先方程两边都除以2,再开方求出答案即可.
【解答】解:2x2=4,
方程两边都除以2得:x2=2,
开方得:x=,
故选:C.
2.若cos30°?sinα=,则锐角α等于( )
A.15°
B.30°
C.45°
D.60°
【分析】直接利用特殊角的三角函数值得出答案.
【解答】解:∵cos30°?sinα=,
∴?sinα=,
∴sinα=×=,
∴锐角α等于为30°.
故选:B.
3.下列函数中,图象是双曲线且经过点(2,﹣4)的是( )
A.y=﹣2x
B.y=﹣
C.y=﹣
D.y=x﹣6
【分析】设出反比例函数的解析式,把(﹣2,1)代入解析式,求出k的值,得到反比例函数的解析式,进行验证即可.
【解答】解:设函数解析式为y=,
把(2,﹣4)代入解析式,得k=2×(﹣4)=﹣8.
故解析式为y=﹣.
故选:C.
4.若x=1是方程x2+mx+3=0的一个根,则方程的另一个根是( )
A.3
B.4
C.﹣3
D.﹣4
【分析】根据根与系数的关系即可求出答案.
【解答】解:设另外一根为α,
由根与系数的关系可知:1×α=3,
∴α=3,
故选:A.
5.用配方法解方程x2﹣4x﹣7=0,可变形为( )
A.(x+2)2=3
B.(x+2)2=11
C.(x﹣2)2=11
D.(x﹣2)2=3
【分析】根据一元二次方程的解法即可求出答案.
【解答】解:∵x2﹣4x﹣7=0,
∴x2﹣4x+4=11,
∴(x﹣2)2=11,
故选:C.
6.已知△ABC∽△A1B1C1,且∠A=50°,∠B=95°,则∠C1等于( )
A.50°
B.95°
C.35°
D.25°
【分析】先由三角形内角和定理求出∠C的度数,再根据相似三角形的对应角相等得出∠C1=∠C.
【解答】解:△ABC中,∵∠A=50°,∠B=95°,
∴∠C=180°﹣∠A﹣∠B=35°,
∵△ABC∽△A1B1C1,
∴∠C1=∠C=35°.
故选:C.
7.当太阳光线与水平地面成30°角时,一棵树的影长为24m,则该树高为( )
A.8m
B.4m
C.12m
D.12m
【分析】根据直角三角形30°角所对的直角边等于斜边的一半可得AB=2BC,再根据勾股定理列式进行计算即可得解.
【解答】解:如图,∵太阳光与水平地面成30°,
∴AB=2BC,
根据勾股定理,AC2+BC2=AB2,
∵影长AC=24m,
∴242+BC2=4BC2,
解得BC=8m.
故选:A.
8.如图,在△ABC中,DE是它的中位线,BC=2,有下面三个结论:①DE=1;②△ADE∽△ABC;③△ADE的面积与△ABC的面积之比为1:4.其中正确结论的个数有( )
A.0个
B.1个
C.2个
D.3个
【分析】①根据中位线的性质结合BC=2,即可得出DE=1,①正确;②由DE是△ABC的中位线可得出DE∥BC,进而得出△ADE∽△ABC,②正确;③由DE是△ABC的中位线可得出点D是线段AB的中点,结合相似三角形的面积之比等于相似比的平方可得出△ADE的面积与△ABC的面积之比为1:4,③正确.综上即可得出结论.
【解答】解:①∵DE是△ABC的中位线,BC=2,
∴DE=BC=1,①正确;
②∵DE是△ABC的中位线,
∴DE∥BC,
∴△ADE∽△ABC,②正确;
③∵DE是△ABC的中位线,
∴点D是线段AB的中点.
∵△ADE∽△ABC,
∴△ADE的面积与△ABC的面积之比为1:4,③正确.
综上所述:正确的结论有①②③.
故选:D.
9.某学校在开展“节约每一滴水”的活动中,从九年级的180名同学中任选出10名同学汇报了各自家庭一个月的节水情况,将有关数据整理成下表:
节水量/t
0.5
1
1.5
2
人数
2
3
4
1
请你估计这180名同学的家庭一个月节约用水的总量大约是( )
A.180t
B.200t
C.216t
D.360t
【分析】先计算这10名同学各自家庭一个月的节水量的平均数,即样本平均数,然后乘以总数180即可解答.
【解答】解:=1.2(t),
180×1.2=216(t),
答:估计这180名同学的家庭一个月节约用水的总量大约是216t.
故选:C.
10.关于x的一元二次方程(k+1)x2+4x﹣1=0有实数根,则k的取值范围是( )
A.k>﹣5
B.k>﹣5且k≠﹣1
C.k≥﹣5
D.k≥﹣5且k≠﹣1
【分析】利用一元二次方程的定义和根的判别式的意义得到k+1≠0且△=42﹣4×(k+1)×(﹣1)≥0,然后求出两个不等式的公共部分即可.
【解答】解:根据题意得k+1≠0且△=42﹣4×(k+1)×(﹣1)≥0,
解得k≥﹣5且k≠﹣1.
故选:D.
二.填空题(共6小题)
11.若,则= ﹣2 .
【分析】根据比例的基本性质,可以用一个数分别表示出a和b,代入原式即可得出结果.
【解答】解:根据题意,
可设a=2k,b=3k.
则==﹣2,
故填﹣2.
12.函数y=中,若x>2,则y的取值范围为 0<y<1 .
【分析】根据反比例函数的性质求解y的取值范围即可.
【解答】解:∵反比例函数y=中,k=2>0.
∴图象在第一象限,
∴y>0,且y随x的增大而减小,
把x=2代入反比例函数y=中,y=1,
∴y的取值范围是0<y<1.
故答案为:0<y<1.
13.设x1,x2分别为一元二次方程x2+2019x+1=0的两个实数根,则x1x2﹣x1﹣x2= 2020 .
【分析】先由根与系数的关系得出x1+x2=﹣2019,x1?x2=1,再代入x1x2﹣x1﹣x2=x1x2﹣(x1+x2)计算可得.
【解答】解:根据题意知x1+x2=﹣2019,x1?x2=1,
则x1x2﹣x1﹣x2
=x1x2﹣(x1+x2)
=1+2019
=2020,
故答案为:2020.
14.如图所示,增加一个条件,可使△ABC∽△AED,这个条件可以是 ∠1=∠B或∠2=∠C或= .
【分析】根据题目所给的条件,利用利用一个三角形的两个角与另一个三角形的两个角对应相等,即可得出答案.此题答案不唯一.再找一个对应角相等的条件即可.
【解答】解:∵∠BAC=∠EAD(公共角),
再由∠1=∠B
或∠2=∠C
或
,
可得△ABC∽△AED,
故答案为:∠1=∠B
或∠2=∠C
或
.
15.将一块长8cm、宽6cm的矩形铁皮的四个角各截去一个面积相同的小正方形,做成一个无盖的盒子,要使盒子的底面积是原来铁皮的面积的,若设盒子的高为xcm,则列出的方程为 x2﹣7x+4=0 .
【分析】首先表示出无盖长方体盒子的底面长为(8﹣2x)cm,宽为(6﹣2x)cm,再根据盒子的底面积是原来铁皮的面积的可得方程(8﹣2x)(6﹣2x)=8×6×.
【解答】解:设盒子的高为xcm,则无盖长方体盒子的底面长为(8﹣2x)cm,宽为(6﹣2x)cm,
由题意得,(8﹣2x)(6﹣2x)=8×6×,
整理得:x2﹣7x+4=0,
故答案为:x2﹣7x+4=0.
16.若反比例函数y=(a是常数)的图象的同一支上有两点(x1,y1),(x2,y2),设b=(x1﹣x2)(y1﹣y2),则一次函数y=bx﹣b的图象不经过第 三 象限.
【分析】根据题意可以判断b的正负,从而可以解答本题.
【解答】解:∵反比例函数y=(a是常数)的图象的同一支上有两点(x1,y1),(x2,y2),b=(x1﹣x2)(y1﹣y2),
∴b=(x1﹣x2)(﹣)=﹣?(a2+1),
∵反比例函数y=(a是常数)的图象的同一支上有两点(x1,y1),(x2,y2),
∴(x1﹣x2)2>0,x1x2>0,a2+1>0,
∴b<0
∴y=bx﹣b不经过第三象限,
故答案为:三.
三.解答题
17解一元二次方程:
(1)x2﹣4x﹣12=0;
(2)(2x﹣1)2=3(2x﹣1).
【考点】解一元二次方程﹣因式分解法.
【专题】一元二次方程及应用;运算能力.
【答案】(1)x1=6,x2=﹣2;
(2)x1=,x2=2.
【分析】(1)利用因式分解法求解可得;
(2)先移项,再利用因式分解法求解可得.
【解答】解:(1)x2﹣4x﹣12=0,
(x﹣6)(x+2)=0,
∴x﹣6=0或x+2=0,
解得x1=6,x2=﹣2;
(2)(2x﹣1)2=3(2x﹣1).
(2x﹣1)2﹣3(2x﹣1)=0,
(2x﹣1)(2x﹣1﹣3)=0,
则2x﹣1=0或2x﹣4=0,
解得x1=,x2=2.
18在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(4,0),B(6,4),C(0,6),将其顶点的坐标缩小为原来的,画出得到的四边形.并判断这两个四边形是位似图形吗?若是,位似比是多少?
【考点】坐标与图形性质;位似变换.
【专题】图形的相似;应用意识.
【答案】画出得到的四边形如图所示,是位似图形,位似比为.
【分析】根据坐标与图形性质画出符合条件的四边形,根据位似图形的概念判断即可.
【解答】解:如图,四边形OA′B′C′即为所画的四边形,
∵四边形OA′B′C′与四边形OABC是相似形、对应点的连线都经过同一点O、对应边平行,
∴四边形OA′B′C′与四边形OABC是位似图形,位似比为.
19如图,在Rt△ABC中,CD是斜边AB上的高.
(1)求证:AC2=AD?AB.
(2)定义:若线段a,b,c满足条件c2=ab,则称c是a,b的比例中项.比如(1)中的AC就是AD,AB的比例中项.请你判断图中CD是不是AD,BD的比例中项?说明理由.
【考点】相似三角形的判定与性质.
【专题】图形的相似;推理能力.
【答案】(1)证明见解答过程;
(2)CD是AD,BD的比例中项.
【分析】(1)证明△ADC∽△ACB,根据相似三角形的性质列出比例式,进而证明结论;
(2)证明△ADC∽△CDB,根据相似三角形的性质、比例中项的定义证明即可.
【解答】(1)证明:∵CD⊥AB,
∴∠ADC=90°,
∴∠ADC=∠ACB,
∵∠A=∠A,
∴△ADC∽△ACB,
∴=,
∴AC2=AD?AB.
(2)解:CD是AD,BD的比例中项,
理由如下:∵∠ACB=90°,
∴∠ACD+∠BCD=90°,
∵∠BCD+∠B=90°,
∴∠ACD=∠B,
∵∠ADC=∠CDB,
∴△ADC∽△CDB,
∴=,
∴CD2=AD?BD,即CD是AD,BD的比例中项.
20如图,四边形ABCD中,∠B=90°,AB=2,CD=8,AC⊥CD,sin∠ACB=.
(1)求AC的长.
(2)求tan∠DAC?cos∠DAC的值.
【考点】角平分线的性质;勾股定理;解直角三角形.
【专题】计算题;解直角三角形及其应用;应用意识.
【答案】(1)6;
(2)(详见解答).
【分析】(1)在Rt△ABC中,利用直角三角形的边角间关系直接得结论
【解答】解:(1)在Rt△ABC中,
∵sin∠ACB==,AB=2,
∴=.
∴AC=6;
(2))在Rt△ADC中,
∵AC=6,CD=8,
∴AD=10.
∵tan∠DAC===,
cos∠DAC===,
∴tan∠DAC?cos∠DAC=×=.
21为执行“均衡教育”政策,某地区2017年投入教育经费2500万元,2019年投入教育经费3025万元.
(1)求2017年至2019年该地区投入教育经费的年平均增长率;
(2)计算一下,该地区2017年到2019年共投入教育经费多少万元?
【考点】一元二次方程的应用.
【专题】增长率问题;应用意识.
【答案】(1)这两年投入教育经费的平均增长率为10%.
(2)该地区2017年到2019年共投入教育经费8275万元.
【分析】(1)一般用增长后的量=增长前的量×(1+增长率),2018年要投入教育经费是2500(1+x)万元,在2018年的基础上再增长x,就是2019年的教育经费数额,即可列出方程求解.
(2)利用(1)中求得的增长率来求2018年该地区将投入教育经费,然后求三年的教育经费的和.
【解答】解:(1)设增长率为x,根据题意2018年为2500(1+x)万元,2019年为2500(1+x)2万元.
则2500(1+x)2=3025,
解得x=0.1=10%,或x=﹣2.1(不合题意舍去).
答:这两年投入教育经费的平均增长率为10%.
(2)根据题意,得2500+2500(1+10%)+3025=8275(万元).
22近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
【考点】用样本估计总体;扇形统计图;条形统计图.
【专题】统计与概率.
【答案】见试题解答内容
【分析】(1)根据B的数量和所占的百分比可以求得本次调查的购买者的人数;
(2)根据统计图中的数据可以求得选择A和D的人数,从而可以将条形统计图补充完整,求得在扇形统计图中A种支付方式所对应的圆心角的度数;
(3)根据统计图中的数据可以计算出使用A和B两种支付方式的购买者共有多少名.
【解答】解:(1)56÷28%=200,
即本次一共调查了200名购买者;
(2)D方式支付的有:200×20%=40(人),
A方式支付的有:200﹣56﹣44﹣40=60(人),
补全的条形统计图如右图所示,
在扇形统计图中A种支付方式所对应的圆心角为:360°×=108°,
故答案为:108;
(3)1600×=928(名),
答:估计使用A和B两种支付方式的购买者共有928名.
23如图,在矩形OABC中,A(3,0),C(0,2),F是AB上的一个动点,F不与A、B重合,过点F的反比例函数y=的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式及△EFA的面积;
(2)当△EFA的面积为时,求F点的坐标.
【考点】反比例函数系数k的几何意义;反比例函数图象上点的坐标特征;矩形的性质.
【专题】反比例函数及其应用;三角形;推理能力.
【答案】(1)y=,S△AEF=;(2)F1(3,),F2(3,).
【分析】(1)先写出点F的坐标,再求k,得到反比例函数解析式,将y=2代入求出点E的坐标,从而求出△EFA的面积;
(2)先求点F的坐标为(3,),再求点E,表示出△EFA的面积,最后求出点F的坐标.
【解答】解:(1)∵点F是AB的中点,A(3,0),C(0,2),
∴F(3,1),AF=1,
∴k=3×1=3,
∴y=,
∴E(,2),
∴BE=,
∴S△AEF=×1×=.
(2)设点F(3,),则AF=,
∵点E的纵坐标为2,
∴E(,2),
∴BE=3﹣,
∴S△AEF=××(3﹣)=,
解得:k1=4,k2=2,
∴F1(3,),F2(3,).
24如图,四边形ABCD中,∠ADC=∠ACB=90°,DC?AC=BC?AD,E为AB的中点,AC交DE于点F.
(1)求证:AC平分∠DAB
(2)求证:=.
(3)若AD,AB的长是x2﹣11x+30=0的两根,求的值.
【考点】解一元二次方程﹣因式分解法;角平分线的性质;直角三角形斜边上的中线;相似三角形的判定与性质.
【专题】证明题;几何综合题;图形的相似;运算能力;推理能力.
【答案】(1)证明过程见解答;
(2)证明过程见解答;
(3).
【分析】(1)欲证明AC平分∠DAB,只要证明△DCA∽△CBA;
(2)根据直角三角形斜边中线的性质可知EC=EA=EB,推出∠DAC=∠EAC=∠ACE即可证明;
(3)由AD∥CE,可得==,由此即可解决问题.
【解答】(1)证明:∵DC?AC=BC?AD,
∵∠ADC=∠ACB=90°,
∴△DCA∽△CBA,
∴∠DAC=∠CAB,
∴AC平分∠DAB;
(2)证明:∵∠ACB=90°,AE=EB,
∴CE=AE=EB,
∴∠EAC=∠ECA,
∵∠DAC=∠CAE,
∴∠DAC=∠ACE,
∴AD∥EC.
∴=;
(3)解:∵AD,AB的长是x2﹣11x+30=0的两根,
∴AD=5,AB=6,
∵∠ACB=90°,AE=EB,
∴CE=AB=3,AD∥CE,
∴==,
∴=.
一.选择题
1.方程2x2=4的解是( )
A.
B.2
C.
D.±2
2.若cos30°?sinα=,则锐角α等于( )
A.15°
B.30°
C.45°
D.60°
3.下列函数中,图象是双曲线且经过点(2,﹣4)的是( )
A.y=﹣2x
B.y=﹣
C.y=﹣
D.y=x﹣6
4.若x=1是方程x2+mx+3=0的一个根,则方程的另一个根是( )
A.3
B.4
C.﹣3
D.﹣4
5.用配方法解方程x2﹣4x﹣7=0,可变形为( )
A.(x+2)2=3
B.(x+2)2=11
C.(x﹣2)2=11
D.(x﹣2)2=3
6.已知△ABC∽△A1B1C1,且∠A=50°,∠B=95°,则∠C1等于( )
A.50°
B.95°
C.35°
D.25°
7.当太阳光线与水平地面成30°角时,一棵树的影长为24m,则该树高为( )
A.8m
B.4m
C.12m
D.12m
8.如图,在△ABC中,DE是它的中位线,BC=2,有下面三个结论:①DE=1;②△ADE∽△ABC;③△ADE的面积与△ABC的面积之比为1:4.其中正确结论的个数有( )
A.0个
B.1个
C.2个
D.3个
9.某学校在开展“节约每一滴水”的活动中,从九年级的180名同学中任选出10名同学汇报了各自家庭一个月的节水情况,将有关数据整理成下表:
节水量/t
0.5
1
1.5
2
人数
2
3
4
1
请你估计这180名同学的家庭一个月节约用水的总量大约是( )
A.180t
B.200t
C.216t
D.360t
10.关于x的一元二次方程(k+1)x2+4x﹣1=0有实数根,则k的取值范围是( )
A.k>﹣5
B.k>﹣5且k≠﹣1
C.k≥﹣5
D.k≥﹣5且k≠﹣1
二.填空题
11.若,则=
.
12.函数y=中,若x>2,则y的取值范围为
.
13.设x1,x2分别为一元二次方程x2+2019x+1=0的两个实数根,则x1x2﹣x1﹣x2=
.
14.如图所示,增加一个条件,可使△ABC∽△AED,这个条件可以是
.
15.将一块长8cm、宽6cm的矩形铁皮的四个角各截去一个面积相同的小正方形,做成一个无盖的盒子,要使盒子的底面积是原来铁皮的面积的,若设盒子的高为xcm,则列出的方程为
.
16.若反比例函数y=(a是常数)的图象的同一支上有两点(x1,y1),(x2,y2),设b=(x1﹣x2)(y1﹣y2),则一次函数y=bx﹣b的图象不经过第
象限.
三.解答题
17解一元二次方程:
(1)x2﹣4x﹣12=0;
(2)(2x﹣1)2=3(2x﹣1).
18在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(4,0),B(6,4),C(0,6),将其顶点的坐标缩小为原来的,画出得到的四边形.并判断这两个四边形是位似图形吗?若是,位似比是多少?
19如图,在Rt△ABC中,CD是斜边AB上的高.
(1)求证:AC2=AD?AB.
(2)定义:若线段a,b,c满足条件c2=ab,则称c是a,b的比例中项.比如(1)中的AC就是AD,AB的比例中项.请你判断图中CD是不是AD,BD的比例中项?说明理由.
20如图,四边形ABCD中,∠B=90°,AB=2,CD=8,AC⊥CD,sin∠ACB=.
(1)求AC的长.
(2)求tan∠DAC?cos∠DAC的值.
21为执行“均衡教育”政策,某地区2017年投入教育经费2500万元,2019年投入教育经费3025万元.
(1)求2017年至2019年该地区投入教育经费的年平均增长率;
(2)计算一下,该地区2017年到2019年共投入教育经费多少万元?
22近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
23如图,在矩形OABC中,A(3,0),C(0,2),F是AB上的一个动点,F不与A、B重合,过点F的反比例函数y=的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式及△EFA的面积;
(2)当△EFA的面积为时,求F点的坐标.
24如图,四边形ABCD中,∠ADC=∠ACB=90°,DC?AC=BC?AD,E为AB的中点,AC交DE于点F.
(1)求证:AC平分∠DAB
(2)求证:=.
(3)若AD,AB的长是x2﹣11x+30=0的两根,求的值.
参考答案与试题解析
一.选择题(共10小题)
1.方程2x2=4的解是( )
A.
B.2
C.
D.±2
【分析】先方程两边都除以2,再开方求出答案即可.
【解答】解:2x2=4,
方程两边都除以2得:x2=2,
开方得:x=,
故选:C.
2.若cos30°?sinα=,则锐角α等于( )
A.15°
B.30°
C.45°
D.60°
【分析】直接利用特殊角的三角函数值得出答案.
【解答】解:∵cos30°?sinα=,
∴?sinα=,
∴sinα=×=,
∴锐角α等于为30°.
故选:B.
3.下列函数中,图象是双曲线且经过点(2,﹣4)的是( )
A.y=﹣2x
B.y=﹣
C.y=﹣
D.y=x﹣6
【分析】设出反比例函数的解析式,把(﹣2,1)代入解析式,求出k的值,得到反比例函数的解析式,进行验证即可.
【解答】解:设函数解析式为y=,
把(2,﹣4)代入解析式,得k=2×(﹣4)=﹣8.
故解析式为y=﹣.
故选:C.
4.若x=1是方程x2+mx+3=0的一个根,则方程的另一个根是( )
A.3
B.4
C.﹣3
D.﹣4
【分析】根据根与系数的关系即可求出答案.
【解答】解:设另外一根为α,
由根与系数的关系可知:1×α=3,
∴α=3,
故选:A.
5.用配方法解方程x2﹣4x﹣7=0,可变形为( )
A.(x+2)2=3
B.(x+2)2=11
C.(x﹣2)2=11
D.(x﹣2)2=3
【分析】根据一元二次方程的解法即可求出答案.
【解答】解:∵x2﹣4x﹣7=0,
∴x2﹣4x+4=11,
∴(x﹣2)2=11,
故选:C.
6.已知△ABC∽△A1B1C1,且∠A=50°,∠B=95°,则∠C1等于( )
A.50°
B.95°
C.35°
D.25°
【分析】先由三角形内角和定理求出∠C的度数,再根据相似三角形的对应角相等得出∠C1=∠C.
【解答】解:△ABC中,∵∠A=50°,∠B=95°,
∴∠C=180°﹣∠A﹣∠B=35°,
∵△ABC∽△A1B1C1,
∴∠C1=∠C=35°.
故选:C.
7.当太阳光线与水平地面成30°角时,一棵树的影长为24m,则该树高为( )
A.8m
B.4m
C.12m
D.12m
【分析】根据直角三角形30°角所对的直角边等于斜边的一半可得AB=2BC,再根据勾股定理列式进行计算即可得解.
【解答】解:如图,∵太阳光与水平地面成30°,
∴AB=2BC,
根据勾股定理,AC2+BC2=AB2,
∵影长AC=24m,
∴242+BC2=4BC2,
解得BC=8m.
故选:A.
8.如图,在△ABC中,DE是它的中位线,BC=2,有下面三个结论:①DE=1;②△ADE∽△ABC;③△ADE的面积与△ABC的面积之比为1:4.其中正确结论的个数有( )
A.0个
B.1个
C.2个
D.3个
【分析】①根据中位线的性质结合BC=2,即可得出DE=1,①正确;②由DE是△ABC的中位线可得出DE∥BC,进而得出△ADE∽△ABC,②正确;③由DE是△ABC的中位线可得出点D是线段AB的中点,结合相似三角形的面积之比等于相似比的平方可得出△ADE的面积与△ABC的面积之比为1:4,③正确.综上即可得出结论.
【解答】解:①∵DE是△ABC的中位线,BC=2,
∴DE=BC=1,①正确;
②∵DE是△ABC的中位线,
∴DE∥BC,
∴△ADE∽△ABC,②正确;
③∵DE是△ABC的中位线,
∴点D是线段AB的中点.
∵△ADE∽△ABC,
∴△ADE的面积与△ABC的面积之比为1:4,③正确.
综上所述:正确的结论有①②③.
故选:D.
9.某学校在开展“节约每一滴水”的活动中,从九年级的180名同学中任选出10名同学汇报了各自家庭一个月的节水情况,将有关数据整理成下表:
节水量/t
0.5
1
1.5
2
人数
2
3
4
1
请你估计这180名同学的家庭一个月节约用水的总量大约是( )
A.180t
B.200t
C.216t
D.360t
【分析】先计算这10名同学各自家庭一个月的节水量的平均数,即样本平均数,然后乘以总数180即可解答.
【解答】解:=1.2(t),
180×1.2=216(t),
答:估计这180名同学的家庭一个月节约用水的总量大约是216t.
故选:C.
10.关于x的一元二次方程(k+1)x2+4x﹣1=0有实数根,则k的取值范围是( )
A.k>﹣5
B.k>﹣5且k≠﹣1
C.k≥﹣5
D.k≥﹣5且k≠﹣1
【分析】利用一元二次方程的定义和根的判别式的意义得到k+1≠0且△=42﹣4×(k+1)×(﹣1)≥0,然后求出两个不等式的公共部分即可.
【解答】解:根据题意得k+1≠0且△=42﹣4×(k+1)×(﹣1)≥0,
解得k≥﹣5且k≠﹣1.
故选:D.
二.填空题(共6小题)
11.若,则= ﹣2 .
【分析】根据比例的基本性质,可以用一个数分别表示出a和b,代入原式即可得出结果.
【解答】解:根据题意,
可设a=2k,b=3k.
则==﹣2,
故填﹣2.
12.函数y=中,若x>2,则y的取值范围为 0<y<1 .
【分析】根据反比例函数的性质求解y的取值范围即可.
【解答】解:∵反比例函数y=中,k=2>0.
∴图象在第一象限,
∴y>0,且y随x的增大而减小,
把x=2代入反比例函数y=中,y=1,
∴y的取值范围是0<y<1.
故答案为:0<y<1.
13.设x1,x2分别为一元二次方程x2+2019x+1=0的两个实数根,则x1x2﹣x1﹣x2= 2020 .
【分析】先由根与系数的关系得出x1+x2=﹣2019,x1?x2=1,再代入x1x2﹣x1﹣x2=x1x2﹣(x1+x2)计算可得.
【解答】解:根据题意知x1+x2=﹣2019,x1?x2=1,
则x1x2﹣x1﹣x2
=x1x2﹣(x1+x2)
=1+2019
=2020,
故答案为:2020.
14.如图所示,增加一个条件,可使△ABC∽△AED,这个条件可以是 ∠1=∠B或∠2=∠C或= .
【分析】根据题目所给的条件,利用利用一个三角形的两个角与另一个三角形的两个角对应相等,即可得出答案.此题答案不唯一.再找一个对应角相等的条件即可.
【解答】解:∵∠BAC=∠EAD(公共角),
再由∠1=∠B
或∠2=∠C
或
,
可得△ABC∽△AED,
故答案为:∠1=∠B
或∠2=∠C
或
.
15.将一块长8cm、宽6cm的矩形铁皮的四个角各截去一个面积相同的小正方形,做成一个无盖的盒子,要使盒子的底面积是原来铁皮的面积的,若设盒子的高为xcm,则列出的方程为 x2﹣7x+4=0 .
【分析】首先表示出无盖长方体盒子的底面长为(8﹣2x)cm,宽为(6﹣2x)cm,再根据盒子的底面积是原来铁皮的面积的可得方程(8﹣2x)(6﹣2x)=8×6×.
【解答】解:设盒子的高为xcm,则无盖长方体盒子的底面长为(8﹣2x)cm,宽为(6﹣2x)cm,
由题意得,(8﹣2x)(6﹣2x)=8×6×,
整理得:x2﹣7x+4=0,
故答案为:x2﹣7x+4=0.
16.若反比例函数y=(a是常数)的图象的同一支上有两点(x1,y1),(x2,y2),设b=(x1﹣x2)(y1﹣y2),则一次函数y=bx﹣b的图象不经过第 三 象限.
【分析】根据题意可以判断b的正负,从而可以解答本题.
【解答】解:∵反比例函数y=(a是常数)的图象的同一支上有两点(x1,y1),(x2,y2),b=(x1﹣x2)(y1﹣y2),
∴b=(x1﹣x2)(﹣)=﹣?(a2+1),
∵反比例函数y=(a是常数)的图象的同一支上有两点(x1,y1),(x2,y2),
∴(x1﹣x2)2>0,x1x2>0,a2+1>0,
∴b<0
∴y=bx﹣b不经过第三象限,
故答案为:三.
三.解答题
17解一元二次方程:
(1)x2﹣4x﹣12=0;
(2)(2x﹣1)2=3(2x﹣1).
【考点】解一元二次方程﹣因式分解法.
【专题】一元二次方程及应用;运算能力.
【答案】(1)x1=6,x2=﹣2;
(2)x1=,x2=2.
【分析】(1)利用因式分解法求解可得;
(2)先移项,再利用因式分解法求解可得.
【解答】解:(1)x2﹣4x﹣12=0,
(x﹣6)(x+2)=0,
∴x﹣6=0或x+2=0,
解得x1=6,x2=﹣2;
(2)(2x﹣1)2=3(2x﹣1).
(2x﹣1)2﹣3(2x﹣1)=0,
(2x﹣1)(2x﹣1﹣3)=0,
则2x﹣1=0或2x﹣4=0,
解得x1=,x2=2.
18在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(4,0),B(6,4),C(0,6),将其顶点的坐标缩小为原来的,画出得到的四边形.并判断这两个四边形是位似图形吗?若是,位似比是多少?
【考点】坐标与图形性质;位似变换.
【专题】图形的相似;应用意识.
【答案】画出得到的四边形如图所示,是位似图形,位似比为.
【分析】根据坐标与图形性质画出符合条件的四边形,根据位似图形的概念判断即可.
【解答】解:如图,四边形OA′B′C′即为所画的四边形,
∵四边形OA′B′C′与四边形OABC是相似形、对应点的连线都经过同一点O、对应边平行,
∴四边形OA′B′C′与四边形OABC是位似图形,位似比为.
19如图,在Rt△ABC中,CD是斜边AB上的高.
(1)求证:AC2=AD?AB.
(2)定义:若线段a,b,c满足条件c2=ab,则称c是a,b的比例中项.比如(1)中的AC就是AD,AB的比例中项.请你判断图中CD是不是AD,BD的比例中项?说明理由.
【考点】相似三角形的判定与性质.
【专题】图形的相似;推理能力.
【答案】(1)证明见解答过程;
(2)CD是AD,BD的比例中项.
【分析】(1)证明△ADC∽△ACB,根据相似三角形的性质列出比例式,进而证明结论;
(2)证明△ADC∽△CDB,根据相似三角形的性质、比例中项的定义证明即可.
【解答】(1)证明:∵CD⊥AB,
∴∠ADC=90°,
∴∠ADC=∠ACB,
∵∠A=∠A,
∴△ADC∽△ACB,
∴=,
∴AC2=AD?AB.
(2)解:CD是AD,BD的比例中项,
理由如下:∵∠ACB=90°,
∴∠ACD+∠BCD=90°,
∵∠BCD+∠B=90°,
∴∠ACD=∠B,
∵∠ADC=∠CDB,
∴△ADC∽△CDB,
∴=,
∴CD2=AD?BD,即CD是AD,BD的比例中项.
20如图,四边形ABCD中,∠B=90°,AB=2,CD=8,AC⊥CD,sin∠ACB=.
(1)求AC的长.
(2)求tan∠DAC?cos∠DAC的值.
【考点】角平分线的性质;勾股定理;解直角三角形.
【专题】计算题;解直角三角形及其应用;应用意识.
【答案】(1)6;
(2)(详见解答).
【分析】(1)在Rt△ABC中,利用直角三角形的边角间关系直接得结论
【解答】解:(1)在Rt△ABC中,
∵sin∠ACB==,AB=2,
∴=.
∴AC=6;
(2))在Rt△ADC中,
∵AC=6,CD=8,
∴AD=10.
∵tan∠DAC===,
cos∠DAC===,
∴tan∠DAC?cos∠DAC=×=.
21为执行“均衡教育”政策,某地区2017年投入教育经费2500万元,2019年投入教育经费3025万元.
(1)求2017年至2019年该地区投入教育经费的年平均增长率;
(2)计算一下,该地区2017年到2019年共投入教育经费多少万元?
【考点】一元二次方程的应用.
【专题】增长率问题;应用意识.
【答案】(1)这两年投入教育经费的平均增长率为10%.
(2)该地区2017年到2019年共投入教育经费8275万元.
【分析】(1)一般用增长后的量=增长前的量×(1+增长率),2018年要投入教育经费是2500(1+x)万元,在2018年的基础上再增长x,就是2019年的教育经费数额,即可列出方程求解.
(2)利用(1)中求得的增长率来求2018年该地区将投入教育经费,然后求三年的教育经费的和.
【解答】解:(1)设增长率为x,根据题意2018年为2500(1+x)万元,2019年为2500(1+x)2万元.
则2500(1+x)2=3025,
解得x=0.1=10%,或x=﹣2.1(不合题意舍去).
答:这两年投入教育经费的平均增长率为10%.
(2)根据题意,得2500+2500(1+10%)+3025=8275(万元).
22近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
【考点】用样本估计总体;扇形统计图;条形统计图.
【专题】统计与概率.
【答案】见试题解答内容
【分析】(1)根据B的数量和所占的百分比可以求得本次调查的购买者的人数;
(2)根据统计图中的数据可以求得选择A和D的人数,从而可以将条形统计图补充完整,求得在扇形统计图中A种支付方式所对应的圆心角的度数;
(3)根据统计图中的数据可以计算出使用A和B两种支付方式的购买者共有多少名.
【解答】解:(1)56÷28%=200,
即本次一共调查了200名购买者;
(2)D方式支付的有:200×20%=40(人),
A方式支付的有:200﹣56﹣44﹣40=60(人),
补全的条形统计图如右图所示,
在扇形统计图中A种支付方式所对应的圆心角为:360°×=108°,
故答案为:108;
(3)1600×=928(名),
答:估计使用A和B两种支付方式的购买者共有928名.
23如图,在矩形OABC中,A(3,0),C(0,2),F是AB上的一个动点,F不与A、B重合,过点F的反比例函数y=的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式及△EFA的面积;
(2)当△EFA的面积为时,求F点的坐标.
【考点】反比例函数系数k的几何意义;反比例函数图象上点的坐标特征;矩形的性质.
【专题】反比例函数及其应用;三角形;推理能力.
【答案】(1)y=,S△AEF=;(2)F1(3,),F2(3,).
【分析】(1)先写出点F的坐标,再求k,得到反比例函数解析式,将y=2代入求出点E的坐标,从而求出△EFA的面积;
(2)先求点F的坐标为(3,),再求点E,表示出△EFA的面积,最后求出点F的坐标.
【解答】解:(1)∵点F是AB的中点,A(3,0),C(0,2),
∴F(3,1),AF=1,
∴k=3×1=3,
∴y=,
∴E(,2),
∴BE=,
∴S△AEF=×1×=.
(2)设点F(3,),则AF=,
∵点E的纵坐标为2,
∴E(,2),
∴BE=3﹣,
∴S△AEF=××(3﹣)=,
解得:k1=4,k2=2,
∴F1(3,),F2(3,).
24如图,四边形ABCD中,∠ADC=∠ACB=90°,DC?AC=BC?AD,E为AB的中点,AC交DE于点F.
(1)求证:AC平分∠DAB
(2)求证:=.
(3)若AD,AB的长是x2﹣11x+30=0的两根,求的值.
【考点】解一元二次方程﹣因式分解法;角平分线的性质;直角三角形斜边上的中线;相似三角形的判定与性质.
【专题】证明题;几何综合题;图形的相似;运算能力;推理能力.
【答案】(1)证明过程见解答;
(2)证明过程见解答;
(3).
【分析】(1)欲证明AC平分∠DAB,只要证明△DCA∽△CBA;
(2)根据直角三角形斜边中线的性质可知EC=EA=EB,推出∠DAC=∠EAC=∠ACE即可证明;
(3)由AD∥CE,可得==,由此即可解决问题.
【解答】(1)证明:∵DC?AC=BC?AD,
∵∠ADC=∠ACB=90°,
∴△DCA∽△CBA,
∴∠DAC=∠CAB,
∴AC平分∠DAB;
(2)证明:∵∠ACB=90°,AE=EB,
∴CE=AE=EB,
∴∠EAC=∠ECA,
∵∠DAC=∠CAE,
∴∠DAC=∠ACE,
∴AD∥EC.
∴=;
(3)解:∵AD,AB的长是x2﹣11x+30=0的两根,
∴AD=5,AB=6,
∵∠ACB=90°,AE=EB,
∴CE=AB=3,AD∥CE,
∴==,
∴=.
同课章节目录
