2020-2021学年安徽省合肥市肥西县七年级(下)期末数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年安徽省合肥市肥西县七年级(下)期末数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 534.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 10:15:48 | ||
图片预览




文档简介
2020-2021学年安徽省合肥市肥西县七年级(下)期末数学试卷
一、选择题(共10小题,每题3分,共30分).
1.下列分式化简结果为的是( )
A. B. C. D.
2.墨迹覆盖了等式“x2x=x3(x≠0)”中的运算符号,则覆盖的是( )
A.+ B.﹣ C.× D.÷
3.下列等式从左到右的变形,属于因式分解的是( )
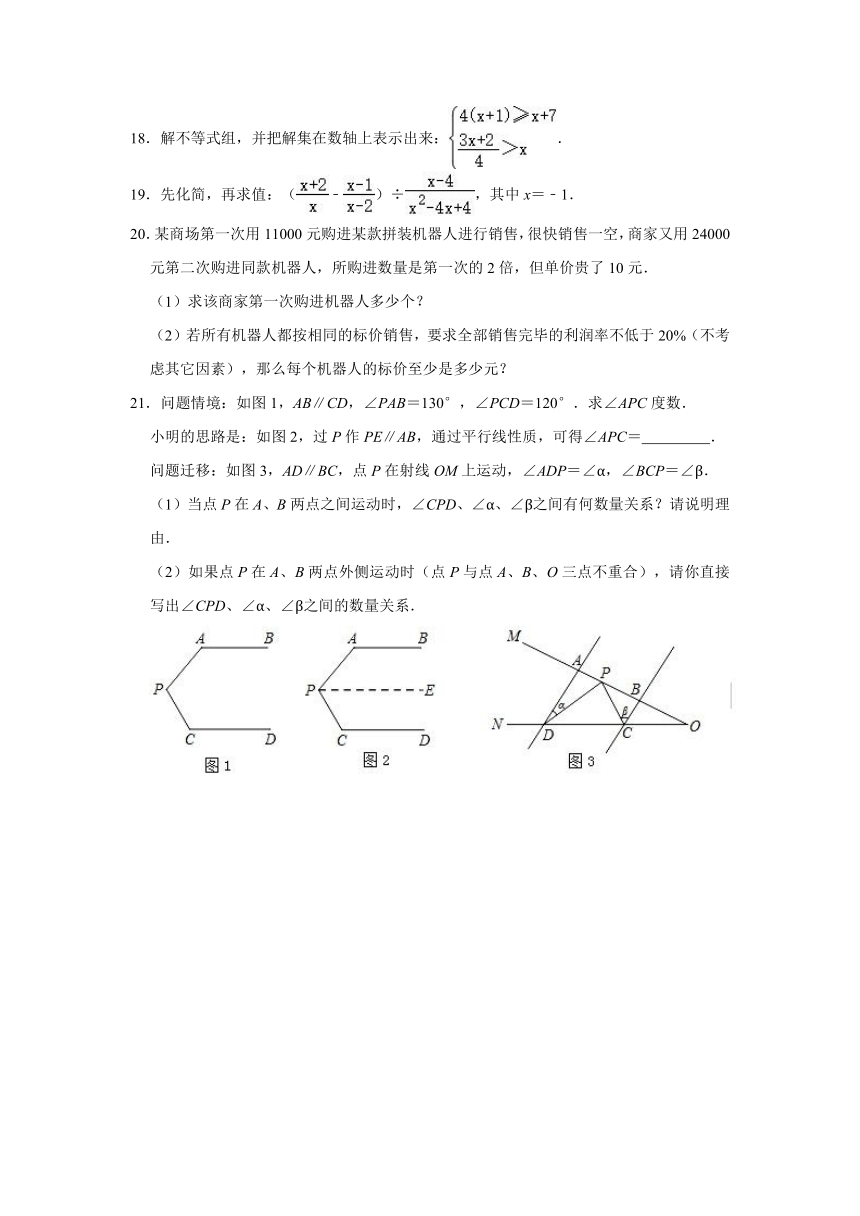
A.a(x﹣y)=ax﹣ay B.x2+2x+1=x(x+2)+1
C.(x+1)(x+3)=x2+4x+3 D.x3﹣x=x(x+1)(x﹣1)
4.+=0,则x的值是( )
A.﹣3 B.﹣1 C. D.无选项
5.若=,则2n﹣3m的值是( )
A.﹣1 B.1 C.2 D.3
6.将一块直角三角尺ABC按如图所示的方式放置,其中点A、C分别落在直线a、b上,若a∥b,∠1=65°,则∠2的度数为( )
A.75° B.65° C.35° D.25°
7.世界上:最薄的纳米材料其理论厚度是0.34m,该数据用科学记数法表示为3.4×10﹣6,则a的值为( )
A.4 B.5 C.6 D.7
8.一个长方形的长增加50%,宽减少50%,那么长方形的面积( )
A.不变 B.增加50% C.减少25% D.不能确定
9.已知a=2019x+2018,b=2019x+2019,c=2019x+2020,则代数式a2+b2+c2﹣ab﹣ac﹣bc的值为( )
A.0 B.1 C.2 D.3
10.将多项式x2+4加上一个整式,使它成为完全平方式,则下列不满足条件的整式是( )
A.﹣4x B.4x C.x4 D.x2
二、填空题(共5小题,每小题3分,满分15分)
11.如图,直线a,b被第三条直线c所截,如果a∥b,∠1=50°,那么∠2= °.
12.把多项式ax2﹣4ax+4a因式分解的结果是 .
13.如图所示,想在河的两岸搭建一座桥,搭建方式最短的是 ,理由是 .
14.若?|m|=,则m= .
15.如果不等式组无解,则a的取值范围是 .
三、解答题(本题共6题,第16、17每小题6分,第18、19题每小题6分,第20题10分,第21题12分,要有解题的主要过程)
16.把下列各数分别填入相应的横线上.
﹣5、|﹣|、0、﹣3.14、、﹣12、﹣、+1.99、﹣(﹣6)、0.1010010001…(每两个1之间依次多一个0)
(1)整数: .
(2)分数: .
(3)无理数: .
17.计算:(﹣2)0+|﹣2|﹣()﹣1﹣(﹣2)3.
18.解不等式组,并把解集在数轴上表示出来:.
19.先化简,再求值:(﹣)÷,其中x=﹣1.
20.某商场第一次用11000元购进某款拼装机器人进行销售,很快销售一空,商家又用24000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进机器人多少个?
(2)若所有机器人都按相同的标价销售,要求全部销售完毕的利润率不低于20%(不考虑其它因素),那么每个机器人的标价至少是多少元?
21.问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数.
小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC= .
问题迁移:如图3,AD∥BC,点P在射线OM上运动,∠ADP=∠α,∠BCP=∠β.
(1)当点P在A、B两点之间运动时,∠CPD、∠α、∠β之间有何数量关系?请说明理由.
(2)如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β之间的数量关系.
参考答案
一、选择题(共10小题,每小题3分,满分30分)
1.下列分式化简结果为的是( )
A. B. C. D.
解:A.,故本选项不符合题意;
B.,故本选项不符合题意;
C.,故本选项符合题意;
D.,故本选项不符合题意;
故选:C.
2.墨迹覆盖了等式“x2x=x3(x≠0)”中的运算符号,则覆盖的是( )
A.+ B.﹣ C.× D.÷
解:∵x2×x=x3(x≠0),
∴覆盖的是:×.
故选:C.
3.下列等式从左到右的变形,属于因式分解的是( )
A.a(x﹣y)=ax﹣ay B.x2+2x+1=x(x+2)+1
C.(x+1)(x+3)=x2+4x+3 D.x3﹣x=x(x+1)(x﹣1)
解:A、右边不是整式积的形式,不是因式分解,故本选项错误;
B、右边不是整式积的形式,不是因式分解,故本选项错误;
C、右边不是整式积的形式,不是因式分解,故本选项错误;
D、符合因式分解的定义,故本选项正确;
故选:D.
4.+=0,则x的值是( )
A.﹣3 B.﹣1 C. D.无选项
解:+=0,
即=﹣,
故有2x﹣1=﹣5x﹣8
解之得x=﹣1,
故选:B.
5.若=,则2n﹣3m的值是( )
A.﹣1 B.1 C.2 D.3
解:∵
=33m÷32n
=33m﹣2n,
=3﹣1,
∴3m﹣2n=﹣1.
∴2n﹣3m=1.
故选:B.
6.将一块直角三角尺ABC按如图所示的方式放置,其中点A、C分别落在直线a、b上,若a∥b,∠1=65°,则∠2的度数为( )
A.75° B.65° C.35° D.25°
解:如图,
∵a∥b,
∴∠3=∠1=65°,
∵∠2+∠3=90°,
∴∠2=90°﹣∠3=90°﹣65°=25°.
故选:D.
7.世界上:最薄的纳米材料其理论厚度是0.34m,该数据用科学记数法表示为3.4×10﹣6,则a的值为( )
A.4 B.5 C.6 D.7
解:∵0.34,该数据用科学记数法表示为3.4×10﹣6,
∴3.4×10﹣6=0.0000034,
则a=5.
故选:B.
8.一个长方形的长增加50%,宽减少50%,那么长方形的面积( )
A.不变 B.增加50% C.减少25% D.不能确定
解:设原来长方形的长与宽分别为a,b,
根据题意得:=﹣25%,
则长方形面积减少25%.
故选:C.
9.已知a=2019x+2018,b=2019x+2019,c=2019x+2020,则代数式a2+b2+c2﹣ab﹣ac﹣bc的值为( )
A.0 B.1 C.2 D.3
解:∵a=2019x+2018,b=2019x+2019,c=2019x+2020,
∴a﹣b=﹣1,b﹣c=﹣1,c﹣a=2,
∴a2+b2+c2﹣ab﹣ac﹣bc
=2(a2+b2+c2﹣ab﹣ac﹣bc)÷2
=[(a﹣b)2+(b﹣c)2+(c﹣a)2]÷2
=[(﹣1)2+(﹣1)2+22]÷2
=6÷2
=3
故选:D.
10.将多项式x2+4加上一个整式,使它成为完全平方式,则下列不满足条件的整式是( )
A.﹣4x B.4x C.x4 D.x2
解:①当x2是平方项时,4±4x+x2=(2±x)2,
则可添加的项是4x或﹣4x,
②当x2是乘积二倍项时,4+x2+x4=(2+x2)2,
则可添加的项是x4.
故选:D.
二、填空题(共5小题,每小题3分,满分15分)
11.如图,直线a,b被第三条直线c所截,如果a∥b,∠1=50°,那么∠2= 130 °.
解:如图,
∵a∥b,∠1=50°,
∴∠1=∠3=50°,
∵∠2+∠3=180°,
∴∠2=180°﹣∠3=180°﹣50°=130°.
故答案为:130.
12.把多项式ax2﹣4ax+4a因式分解的结果是 a(x﹣2)2 .
解:ax2﹣4ax+4a
=a(x2﹣4x+4)
=a(x﹣2)2.
故答案为:a(x﹣2)2.
13.如图所示,想在河的两岸搭建一座桥,搭建方式最短的是 PM ,理由是 垂线段最短 .
解:
∵PM⊥MN,
∴由垂线段最短可知PM是最短的,
故答案为:PM,垂线段最短.
14.若?|m|=,则m= 3或﹣1 .
解:由题意得,
m﹣1≠0,
则m≠1,
(m﹣3)?|m|=m﹣3,
∴(m﹣3)?(|m|﹣1)=0,
∴m=3或m=±1,
∵m≠1,
∴m=3或m=﹣1,
故答案为:3或﹣1.
15.如果不等式组无解,则a的取值范围是 a≤1 .
解:解不等式x﹣1>0,得x>1,
解不等式x﹣a<0,x<a.
∵不等式组无解,
∴a≤1.
故答案为:a≤1.
三、解答题(本题共6题,第16、17每小题6分,第18、19题每小题6分,第20题10分,第21题12分,要有解题的主要过程)
16.把下列各数分别填入相应的横线上.
﹣5、|﹣|、0、﹣3.14、、﹣12、﹣、+1.99、﹣(﹣6)、0.1010010001…(每两个1之间依次多一个0)
(1)整数: ﹣5、0、﹣12、﹣(﹣6) .
(2)分数: |﹣|、﹣3.14、、+1.99 .
(3)无理数: 、0.1010010001…(每两个1之间依次多一个0) .
解:(1)整数包括正整数、负整数和0.所以属于整数的有:﹣5、0、﹣12、﹣(﹣6).
(2)分数还包括有限小数和循环小数,所以属于分数的有:|﹣|、﹣3.14、、+1.99.
(3)无限不循环小数是无理数,所以属于无理数的有:、0.1010010001…(每两个1之间依次多一个0).
答案为:(1)﹣5、0、﹣12、﹣(﹣6),
(2)|﹣|、﹣3.14、、+1.99,
(3)、0.1010010001…(每两个1之间依次多一个0).
17.计算:(﹣2)0+|﹣2|﹣()﹣1﹣(﹣2)3.
解:原式=1+(2﹣)﹣2﹣(﹣8)
=1+2﹣﹣2+8
=9﹣.
18.解不等式组,并把解集在数轴上表示出来:.
解:,
由①得:x≥1,
由②得:x<2,
不等式组的解集为:1≤x<2,
在数轴上表示:
.
19.先化简,再求值:(﹣)÷,其中x=﹣1.
解:原式=?=?=,
当x=﹣1时,原式==3.
20.某商场第一次用11000元购进某款拼装机器人进行销售,很快销售一空,商家又用24000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进机器人多少个?
(2)若所有机器人都按相同的标价销售,要求全部销售完毕的利润率不低于20%(不考虑其它因素),那么每个机器人的标价至少是多少元?
解:(1)设该商家第一次购进机器人x个,
依题意得:+10=,
解得x=100.
经检验x=100是所列方程的解,且符合题意.
答:该商家第一次购进机器人100个.
(2)设每个机器人的标价是a元.
则依题意得:(100+200)a﹣11000﹣24000≥(11000+24000)×20%,
解得a≥140.
答:每个机器人的标价至少是140元.
21.问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数.
小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC= 110° .
问题迁移:如图3,AD∥BC,点P在射线OM上运动,∠ADP=∠α,∠BCP=∠β.
(1)当点P在A、B两点之间运动时,∠CPD、∠α、∠β之间有何数量关系?请说明理由.
(2)如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β之间的数量关系.
解:过P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠APE=180°﹣∠A=50°,∠CPE=180°﹣∠C=60°,
∴∠APC=50°+60°=110°,
故答案为:110°;
(1)∠CPD=∠α+∠β,理由如下:
如图3,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE+∠CPE=∠α+∠β;
(2)当P在BA延长线时,∠CPD=∠β﹣∠α;
理由:如图4,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠CPE﹣∠DPE=∠β﹣∠α;
当P在BO之间时,∠CPD=∠α﹣∠β.
理由:如图5,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE﹣∠CPE=∠α﹣∠β.
一、选择题(共10小题,每题3分,共30分).
1.下列分式化简结果为的是( )
A. B. C. D.
2.墨迹覆盖了等式“x2x=x3(x≠0)”中的运算符号,则覆盖的是( )
A.+ B.﹣ C.× D.÷
3.下列等式从左到右的变形,属于因式分解的是( )
A.a(x﹣y)=ax﹣ay B.x2+2x+1=x(x+2)+1
C.(x+1)(x+3)=x2+4x+3 D.x3﹣x=x(x+1)(x﹣1)
4.+=0,则x的值是( )
A.﹣3 B.﹣1 C. D.无选项
5.若=,则2n﹣3m的值是( )
A.﹣1 B.1 C.2 D.3
6.将一块直角三角尺ABC按如图所示的方式放置,其中点A、C分别落在直线a、b上,若a∥b,∠1=65°,则∠2的度数为( )
A.75° B.65° C.35° D.25°
7.世界上:最薄的纳米材料其理论厚度是0.34m,该数据用科学记数法表示为3.4×10﹣6,则a的值为( )
A.4 B.5 C.6 D.7
8.一个长方形的长增加50%,宽减少50%,那么长方形的面积( )
A.不变 B.增加50% C.减少25% D.不能确定
9.已知a=2019x+2018,b=2019x+2019,c=2019x+2020,则代数式a2+b2+c2﹣ab﹣ac﹣bc的值为( )
A.0 B.1 C.2 D.3
10.将多项式x2+4加上一个整式,使它成为完全平方式,则下列不满足条件的整式是( )
A.﹣4x B.4x C.x4 D.x2
二、填空题(共5小题,每小题3分,满分15分)
11.如图,直线a,b被第三条直线c所截,如果a∥b,∠1=50°,那么∠2= °.
12.把多项式ax2﹣4ax+4a因式分解的结果是 .
13.如图所示,想在河的两岸搭建一座桥,搭建方式最短的是 ,理由是 .
14.若?|m|=,则m= .
15.如果不等式组无解,则a的取值范围是 .
三、解答题(本题共6题,第16、17每小题6分,第18、19题每小题6分,第20题10分,第21题12分,要有解题的主要过程)
16.把下列各数分别填入相应的横线上.
﹣5、|﹣|、0、﹣3.14、、﹣12、﹣、+1.99、﹣(﹣6)、0.1010010001…(每两个1之间依次多一个0)
(1)整数: .
(2)分数: .
(3)无理数: .
17.计算:(﹣2)0+|﹣2|﹣()﹣1﹣(﹣2)3.
18.解不等式组,并把解集在数轴上表示出来:.
19.先化简,再求值:(﹣)÷,其中x=﹣1.
20.某商场第一次用11000元购进某款拼装机器人进行销售,很快销售一空,商家又用24000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进机器人多少个?
(2)若所有机器人都按相同的标价销售,要求全部销售完毕的利润率不低于20%(不考虑其它因素),那么每个机器人的标价至少是多少元?
21.问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数.
小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC= .
问题迁移:如图3,AD∥BC,点P在射线OM上运动,∠ADP=∠α,∠BCP=∠β.
(1)当点P在A、B两点之间运动时,∠CPD、∠α、∠β之间有何数量关系?请说明理由.
(2)如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β之间的数量关系.
参考答案
一、选择题(共10小题,每小题3分,满分30分)
1.下列分式化简结果为的是( )
A. B. C. D.
解:A.,故本选项不符合题意;
B.,故本选项不符合题意;
C.,故本选项符合题意;
D.,故本选项不符合题意;
故选:C.
2.墨迹覆盖了等式“x2x=x3(x≠0)”中的运算符号,则覆盖的是( )
A.+ B.﹣ C.× D.÷
解:∵x2×x=x3(x≠0),
∴覆盖的是:×.
故选:C.
3.下列等式从左到右的变形,属于因式分解的是( )
A.a(x﹣y)=ax﹣ay B.x2+2x+1=x(x+2)+1
C.(x+1)(x+3)=x2+4x+3 D.x3﹣x=x(x+1)(x﹣1)
解:A、右边不是整式积的形式,不是因式分解,故本选项错误;
B、右边不是整式积的形式,不是因式分解,故本选项错误;
C、右边不是整式积的形式,不是因式分解,故本选项错误;
D、符合因式分解的定义,故本选项正确;
故选:D.
4.+=0,则x的值是( )
A.﹣3 B.﹣1 C. D.无选项
解:+=0,
即=﹣,
故有2x﹣1=﹣5x﹣8
解之得x=﹣1,
故选:B.
5.若=,则2n﹣3m的值是( )
A.﹣1 B.1 C.2 D.3
解:∵
=33m÷32n
=33m﹣2n,
=3﹣1,
∴3m﹣2n=﹣1.
∴2n﹣3m=1.
故选:B.
6.将一块直角三角尺ABC按如图所示的方式放置,其中点A、C分别落在直线a、b上,若a∥b,∠1=65°,则∠2的度数为( )
A.75° B.65° C.35° D.25°
解:如图,
∵a∥b,
∴∠3=∠1=65°,
∵∠2+∠3=90°,
∴∠2=90°﹣∠3=90°﹣65°=25°.
故选:D.
7.世界上:最薄的纳米材料其理论厚度是0.34m,该数据用科学记数法表示为3.4×10﹣6,则a的值为( )
A.4 B.5 C.6 D.7
解:∵0.34,该数据用科学记数法表示为3.4×10﹣6,
∴3.4×10﹣6=0.0000034,
则a=5.
故选:B.
8.一个长方形的长增加50%,宽减少50%,那么长方形的面积( )
A.不变 B.增加50% C.减少25% D.不能确定
解:设原来长方形的长与宽分别为a,b,
根据题意得:=﹣25%,
则长方形面积减少25%.
故选:C.
9.已知a=2019x+2018,b=2019x+2019,c=2019x+2020,则代数式a2+b2+c2﹣ab﹣ac﹣bc的值为( )
A.0 B.1 C.2 D.3
解:∵a=2019x+2018,b=2019x+2019,c=2019x+2020,
∴a﹣b=﹣1,b﹣c=﹣1,c﹣a=2,
∴a2+b2+c2﹣ab﹣ac﹣bc
=2(a2+b2+c2﹣ab﹣ac﹣bc)÷2
=[(a﹣b)2+(b﹣c)2+(c﹣a)2]÷2
=[(﹣1)2+(﹣1)2+22]÷2
=6÷2
=3
故选:D.
10.将多项式x2+4加上一个整式,使它成为完全平方式,则下列不满足条件的整式是( )
A.﹣4x B.4x C.x4 D.x2
解:①当x2是平方项时,4±4x+x2=(2±x)2,
则可添加的项是4x或﹣4x,
②当x2是乘积二倍项时,4+x2+x4=(2+x2)2,
则可添加的项是x4.
故选:D.
二、填空题(共5小题,每小题3分,满分15分)
11.如图,直线a,b被第三条直线c所截,如果a∥b,∠1=50°,那么∠2= 130 °.
解:如图,
∵a∥b,∠1=50°,
∴∠1=∠3=50°,
∵∠2+∠3=180°,
∴∠2=180°﹣∠3=180°﹣50°=130°.
故答案为:130.
12.把多项式ax2﹣4ax+4a因式分解的结果是 a(x﹣2)2 .
解:ax2﹣4ax+4a
=a(x2﹣4x+4)
=a(x﹣2)2.
故答案为:a(x﹣2)2.
13.如图所示,想在河的两岸搭建一座桥,搭建方式最短的是 PM ,理由是 垂线段最短 .
解:
∵PM⊥MN,
∴由垂线段最短可知PM是最短的,
故答案为:PM,垂线段最短.
14.若?|m|=,则m= 3或﹣1 .
解:由题意得,
m﹣1≠0,
则m≠1,
(m﹣3)?|m|=m﹣3,
∴(m﹣3)?(|m|﹣1)=0,
∴m=3或m=±1,
∵m≠1,
∴m=3或m=﹣1,
故答案为:3或﹣1.
15.如果不等式组无解,则a的取值范围是 a≤1 .
解:解不等式x﹣1>0,得x>1,
解不等式x﹣a<0,x<a.
∵不等式组无解,
∴a≤1.
故答案为:a≤1.
三、解答题(本题共6题,第16、17每小题6分,第18、19题每小题6分,第20题10分,第21题12分,要有解题的主要过程)
16.把下列各数分别填入相应的横线上.
﹣5、|﹣|、0、﹣3.14、、﹣12、﹣、+1.99、﹣(﹣6)、0.1010010001…(每两个1之间依次多一个0)
(1)整数: ﹣5、0、﹣12、﹣(﹣6) .
(2)分数: |﹣|、﹣3.14、、+1.99 .
(3)无理数: 、0.1010010001…(每两个1之间依次多一个0) .
解:(1)整数包括正整数、负整数和0.所以属于整数的有:﹣5、0、﹣12、﹣(﹣6).
(2)分数还包括有限小数和循环小数,所以属于分数的有:|﹣|、﹣3.14、、+1.99.
(3)无限不循环小数是无理数,所以属于无理数的有:、0.1010010001…(每两个1之间依次多一个0).
答案为:(1)﹣5、0、﹣12、﹣(﹣6),
(2)|﹣|、﹣3.14、、+1.99,
(3)、0.1010010001…(每两个1之间依次多一个0).
17.计算:(﹣2)0+|﹣2|﹣()﹣1﹣(﹣2)3.
解:原式=1+(2﹣)﹣2﹣(﹣8)
=1+2﹣﹣2+8
=9﹣.
18.解不等式组,并把解集在数轴上表示出来:.
解:,
由①得:x≥1,
由②得:x<2,
不等式组的解集为:1≤x<2,
在数轴上表示:
.
19.先化简,再求值:(﹣)÷,其中x=﹣1.
解:原式=?=?=,
当x=﹣1时,原式==3.
20.某商场第一次用11000元购进某款拼装机器人进行销售,很快销售一空,商家又用24000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进机器人多少个?
(2)若所有机器人都按相同的标价销售,要求全部销售完毕的利润率不低于20%(不考虑其它因素),那么每个机器人的标价至少是多少元?
解:(1)设该商家第一次购进机器人x个,
依题意得:+10=,
解得x=100.
经检验x=100是所列方程的解,且符合题意.
答:该商家第一次购进机器人100个.
(2)设每个机器人的标价是a元.
则依题意得:(100+200)a﹣11000﹣24000≥(11000+24000)×20%,
解得a≥140.
答:每个机器人的标价至少是140元.
21.问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数.
小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC= 110° .
问题迁移:如图3,AD∥BC,点P在射线OM上运动,∠ADP=∠α,∠BCP=∠β.
(1)当点P在A、B两点之间运动时,∠CPD、∠α、∠β之间有何数量关系?请说明理由.
(2)如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β之间的数量关系.
解:过P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠APE=180°﹣∠A=50°,∠CPE=180°﹣∠C=60°,
∴∠APC=50°+60°=110°,
故答案为:110°;
(1)∠CPD=∠α+∠β,理由如下:
如图3,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE+∠CPE=∠α+∠β;
(2)当P在BA延长线时,∠CPD=∠β﹣∠α;
理由:如图4,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠CPE﹣∠DPE=∠β﹣∠α;
当P在BO之间时,∠CPD=∠α﹣∠β.
理由:如图5,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE﹣∠CPE=∠α﹣∠β.
同课章节目录
