2020-2021学年山东省烟台市福山区七年级(下)期末数学试卷(五四学制) (Word版含解析)
文档属性
| 名称 | 2020-2021学年山东省烟台市福山区七年级(下)期末数学试卷(五四学制) (Word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 00:00:00 | ||
图片预览


文档简介
2020-2021学年山东省烟台市福山区七年级(下)期末数学试卷(五四学制)
一、选择题(本题共12个小题,每小题3分,满分36分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的
1.已知a<b,下列式子不一定成立的是( )
A.a﹣1<b﹣1 B.﹣2a>﹣2b
C.ma>mb D.a+1<b+1
2.下列四个命题:
①两直线平行,内错角相等;
②对顶角相等;
③等腰三角形的两个底角相等;
④同角(或等角)的余角相等.
其中逆命题是真命题的是( )
A.① B.①③ C.①③④ D.①②③④
3.不等式组的解集在数轴上表示正确的是( )
A.
B.
C.
D.
4.将一把直尺和一块含30°角的直角三角板按如图所示方式摆放,其中∠CBD=90°,∠BDC=30°,若∠1=78°,则∠2的度数为( )
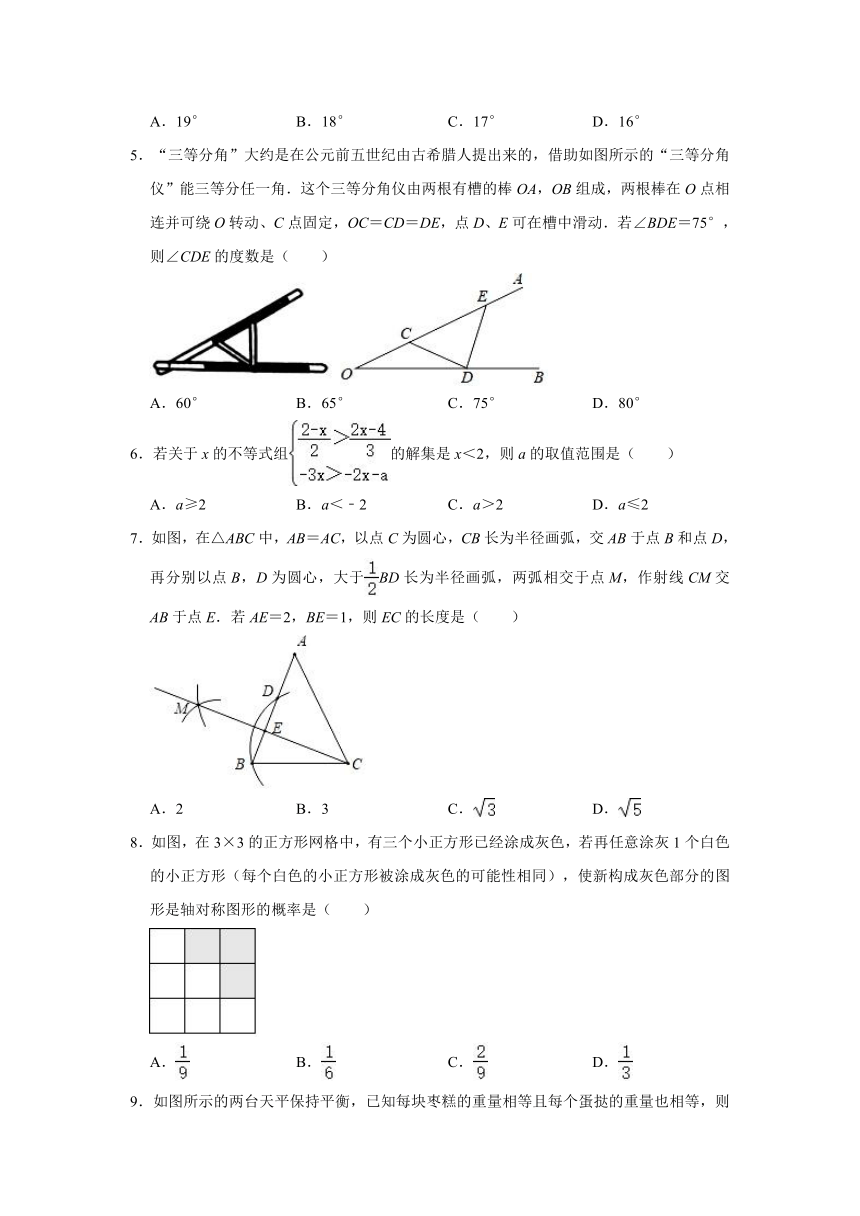
A.19° B.18° C.17° D.16°
5.“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动、C点固定,OC=CD=DE,点D、E可在槽中滑动.若∠BDE=75°,则∠CDE的度数是( )
A.60° B.65° C.75° D.80°
6.若关于x的不等式组的解集是x<2,则a的取值范围是( )
A.a≥2 B.a<﹣2 C.a>2 D.a≤2
7.如图,在△ABC中,AB=AC,以点C为圆心,CB长为半径画弧,交AB于点B和点D,再分别以点B,D为圆心,大于BD长为半径画弧,两弧相交于点M,作射线CM交AB于点E.若AE=2,BE=1,则EC的长度是( )
A.2 B.3 C. D.
8.如图,在3×3的正方形网格中,有三个小正方形已经涂成灰色,若再任意涂灰1个白色的小正方形(每个白色的小正方形被涂成灰色的可能性相同),使新构成灰色部分的图形是轴对称图形的概率是( )
A. B. C. D.
9.如图所示的两台天平保持平衡,已知每块枣糕的重量相等且每个蛋挞的重量也相等,则每块枣糕和每个蛋挞的重量相差( )
A.8g B.6g C.5g D.4g
10.我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知3匹小马能拉1片瓦,1匹大马能拉3片瓦,求小马,大马各有多少匹.若设小马有x匹,大马有y匹,则下列方程组中正确的是( )
A. B.
C. D.
11.数形结合是解决数学问题常用的思想方法.如图,直线y=x+5和直线y=ax+b相交于点P,根据图象可知,方程x+5=ax+b的解是( )
A.x=20 B.x=5 C.x=25 D.x=15
12.如图,已知△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=90°,BD,CE交于点F,连接AF.下列结论:①BD=CE;②BF⊥CF;③AF平分∠CAD;④∠AFE=45°.其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本题共6个小题,每小题3分,满分18分)
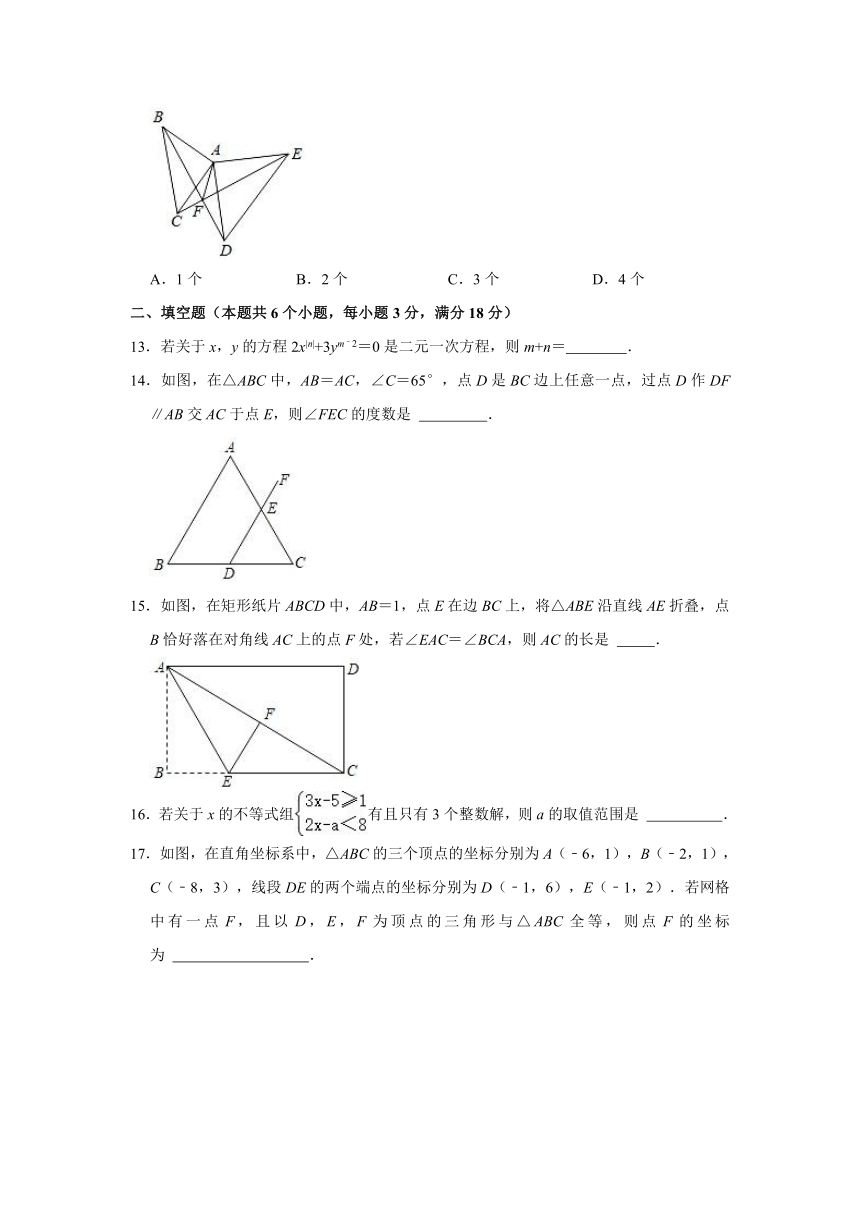
13.若关于x,y的方程2x|n|+3ym﹣2=0是二元一次方程,则m+n= .
14.如图,在△ABC中,AB=AC,∠C=65°,点D是BC边上任意一点,过点D作DF∥AB交AC于点E,则∠FEC的度数是 .
15.如图,在矩形纸片ABCD中,AB=1,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠BCA,则AC的长是 .
16.若关于x的不等式组有且只有3个整数解,则a的取值范围是 .
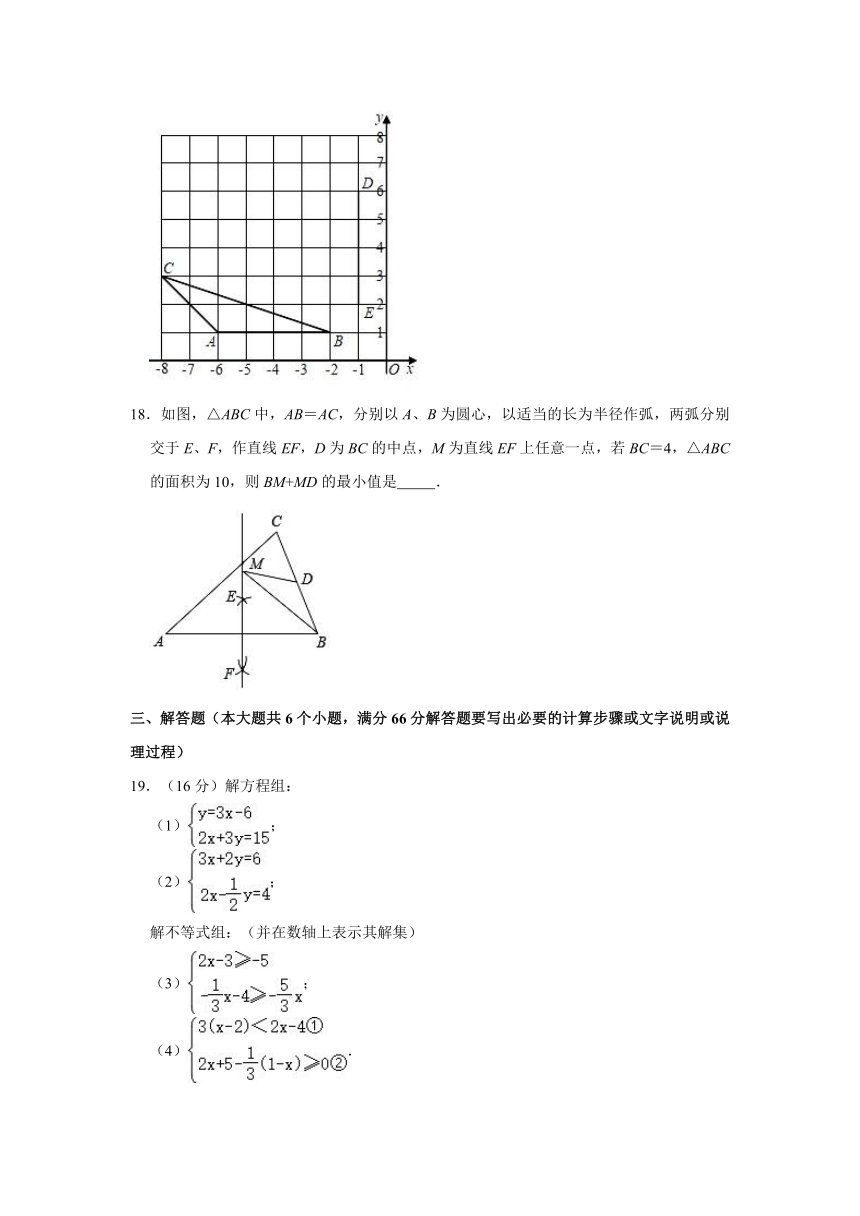
17.如图,在直角坐标系中,△ABC的三个顶点的坐标分别为A(﹣6,1),B(﹣2,1),C(﹣8,3),线段DE的两个端点的坐标分别为D(﹣1,6),E(﹣1,2).若网格中有一点F,且以D,E,F为顶点的三角形与△ABC全等,则点F的坐标为 .
18.如图,△ABC中,AB=AC,分别以A、B为圆心,以适当的长为半径作弧,两弧分别交于E、F,作直线EF,D为BC的中点,M为直线EF上任意一点,若BC=4,△ABC的面积为10,则BM+MD的最小值是 .
三、解答题(本大题共6个小题,满分66分解答题要写出必要的计算步骤或文字说明或说理过程)
19.(16分)解方程组:
(1);
(2);
解不等式组:(并在数轴上表示其解集)
(3);
(4).
20.如图,在平面直角坐标系中,直线y=﹣x﹣1与直线y=﹣2x+2相交于点P,并分别与x轴相交于点A、B.
(1)求交点P的坐标;
(2)求△PAB的面积;
(3)请把图象中直线y=﹣2x+2在直线y=﹣x﹣1上方的部分描黑加粗,并写出此时自变量x的取值范围.
21.如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数.
22.某商场为了吸引顾客,设立了一个翻奖牌(表1中的奖牌对应的奖品一种排法如表2,其中钱数为购物券),并规定:顾客购买不少于200元的商品,就能获得一次翻牌的机会.甲顾客购物220元.
表1:
1 2 3
4 5 6
7 8 9
表2:
20元 50元 谢谢参与
100元 20元 50元
20元 20元 20元
(1)甲顾客得到100元购物券的概率是多少?她获得购物券的概率是多少?
(2)请你根据本题题意写出一个事件,使这个事件发生的概率为.
23.A,B两地相距200千米.早上8:00货车甲从A地出发将一批物资运往B地,行驶一段路程后出现故障,即刻停车与B地联系.B地收到消息后立即派货车乙从B地出发去接运甲车上的物资.货车乙遇到甲后,用了18分钟将物资从货车甲搬运到货车乙上,随后开往B地.两辆货车离开各自出发地的路程y(千米)与时间x(小时)的函数关系如图所示.(通话等其他时间忽略不计)
(1)求货车乙在遇到货车甲前,它离开出发地的路程y关于x的函数表达式.
(2)因实际需要,要求货车乙到达B地的时间比货车甲按原来的速度正常到达B地的时间最多晚1个小时,问货车乙返回B地的速度至少为每小时多少千米?
24.某中学为了庆祝“建党一百周年”,计划举行阳光体育运动比赛,决定让各班购买跳绳和毽子作为活动器材.已知购买2根跳绳和5个毽子共需32元;购买4根跳绳和3个毽子共需36元.
(1)求购买一根跳绳和一个毽子分别需要多少元?
(2)某班需要购买跳绳和毽子的总数量是54,且购买的总费用不能超过260元;若要求购买跳绳的数量多于20根,通过计算说明共有哪几种购买跳绳的方案.
四、附加题(本大题共2个题.满分30分本题要写出必要的计算步骤或文字说明或说理过程)
25.如图,△ABC和△DCE都是等边三角形.
(1)△BCD与△ACE是否全等?若全等,加以证明;若不全等,请说明理由.
(2)若B、C、E三点不在一条直线上,∠ADC=30°,AD=3,CD=2,求BD的长.
26.(16分)在Rt△ABC中,∠ACB=90°,AC=BC,D为AB的中点.
(1)如图1,E,F分别是AC,BC上的点,且AE=CF,请判断△DEF的形状,请写出证明过程.
(2)如图2,若E,F分别分别在CA,BC的延长线上,AB=CF,(1)中的结论是否仍然成立,若成立,写出完整的证明过程;若不成立,请说出理由.
参考答案
一、选择题(本题共12个小题,每小题3分,满分36分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的
1.已知a<b,下列式子不一定成立的是( )
A.a﹣1<b﹣1 B.﹣2a>﹣2b
C.ma>mb D.a+1<b+1
解:A、因为a<b,则a﹣1<b﹣1,所以A选项不符合题意;
B、因为a<b,则﹣2a>﹣2b,所以B选项不符合题意;
C、因为a<b,则当m<0时,ma>mb,所以C选项符合题意;
D、因为a<b,则a<b,所以a+1<b+1,所以D选项不符合题意.
故选:C.
2.下列四个命题:
①两直线平行,内错角相等;
②对顶角相等;
③等腰三角形的两个底角相等;
④同角(或等角)的余角相等.
其中逆命题是真命题的是( )
A.① B.①③ C.①③④ D.①②③④
解:①两直线平行,内错角相等的逆命题是内错角相等,两直线平行,逆命题是真命题;
②对顶角相等的逆命题是相等的角是对顶角,逆命题是假命题;
③等腰三角形的两个底角相等的逆命题是两个角相等的三角形是等腰三角形,逆命题是真命题;
④同角(或等角)的余角相等的逆命题是如果两个的余角相等则这两个角是同角(或等角),逆命题是真命题;
故选:C.
3.不等式组的解集在数轴上表示正确的是( )
A.
B.
C.
D.
解:不等式组,
由①得:x<2,
由②得:x≥﹣1,
∴不等式组的解集为﹣1≤x<2.
表示为:
故选:A.
4.将一把直尺和一块含30°角的直角三角板按如图所示方式摆放,其中∠CBD=90°,∠BDC=30°,若∠1=78°,则∠2的度数为( )
A.19° B.18° C.17° D.16°
解:∵∠CBD=90°,∠1=78°,
∴∠DBE=180°﹣∠CBD﹣∠1=180°﹣90°﹣78°=12°,
∵直尺的两边平行,即EA∥GH,
∴∠BDF=∠DBE=12°,
∵∠BDC=30°,
∴∠2=∠BDC﹣∠BDF=30°﹣12°=18°,
故选:B.
5.“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动、C点固定,OC=CD=DE,点D、E可在槽中滑动.若∠BDE=75°,则∠CDE的度数是( )
A.60° B.65° C.75° D.80°
解:∵OC=CD=DE,
∴∠O=∠ODC,∠DCE=∠DEC,
∴∠DCE=∠O+∠ODC=2∠ODC,
∵∠O+∠OED=3∠ODC=∠BDE=75°,
∴∠ODC=25°,
∵∠CDE+∠ODC=180°﹣∠BDE=105°,
∴∠CDE=105°﹣∠ODC=80°.
故选:D.
6.若关于x的不等式组的解集是x<2,则a的取值范围是( )
A.a≥2 B.a<﹣2 C.a>2 D.a≤2
解:解不等式组,
由①可得:x<2,
由②可得:x<a,
因为关于x的不等式组的解集是x<2,
所以,a≥2,
故选:A.
7.如图,在△ABC中,AB=AC,以点C为圆心,CB长为半径画弧,交AB于点B和点D,再分别以点B,D为圆心,大于BD长为半径画弧,两弧相交于点M,作射线CM交AB于点E.若AE=2,BE=1,则EC的长度是( )
A.2 B.3 C. D.
解:由作法得CE⊥AB,则∠AEC=90°,
AC=AB=BE+AE=2+1=3,
在Rt△ACE中,CE==.
故选:D.
8.如图,在3×3的正方形网格中,有三个小正方形已经涂成灰色,若再任意涂灰1个白色的小正方形(每个白色的小正方形被涂成灰色的可能性相同),使新构成灰色部分的图形是轴对称图形的概率是( )
A. B. C. D.
解:如图所示:当1,2两个分别涂成灰色,新构成灰色部分的图形是轴对称图形,
故新构成灰色部分的图形是轴对称图形的概率是:=.
故选:D.
9.如图所示的两台天平保持平衡,已知每块枣糕的重量相等且每个蛋挞的重量也相等,则每块枣糕和每个蛋挞的重量相差( )
A.8g B.6g C.5g D.4g
解:设枣糕的重量为xg,蛋挞的重量为yg,
由题意得,
解得,
∴y﹣x=12﹣8=4(g),
故选:D.
10.我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知3匹小马能拉1片瓦,1匹大马能拉3片瓦,求小马,大马各有多少匹.若设小马有x匹,大马有y匹,则下列方程组中正确的是( )
A. B.
C. D.
解:根据题意可得:,
故选:C.
11.数形结合是解决数学问题常用的思想方法.如图,直线y=x+5和直线y=ax+b相交于点P,根据图象可知,方程x+5=ax+b的解是( )
A.x=20 B.x=5 C.x=25 D.x=15
解:∵直线y=x+5和直线y=ax+b相交于点P(20,25)
∴方程x+5=ax+b的解为x=20.
故选:A.
12.如图,已知△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=90°,BD,CE交于点F,连接AF.下列结论:①BD=CE;②BF⊥CF;③AF平分∠CAD;④∠AFE=45°.其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
解:如图,作AM⊥BD于M,AN⊥EC于N,设AD交EF于O.
∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴△BAD≌△CAE(SAS),
∴EC=BD,∠BDA=∠AEC,故①正确
∵∠DOF=∠AOE,
∴∠DFO=∠EAO=90°,
∴BD⊥EC,故②正确,
∵△BAD≌△CAE,AM⊥BD,AN⊥EC,
∴AM=AN,
∴FA平分∠EFB,
∴∠AFE=45°,故④正确,
若③成立,则∠EAF=∠BAF,
∵∠AFE=∠AFB,
∴∠AEF=∠ABD=∠ADB,推出AB=AD,由题意知,AB不一定等于AD,
所以AF不一定平分∠CAD,故③错误,
故选:C.
二、填空题(本题共6个小题,每小题3分,满分18分)
13.若关于x,y的方程2x|n|+3ym﹣2=0是二元一次方程,则m+n= 2或4 .
解:根据题意得:|n|=1,m﹣2=1,
解得:n=±1,m=3,
∴m+n=3+1=4,m+n=3﹣1=2,
∴m+n的值是2或4,
故答案为:2或4.
14.如图,在△ABC中,AB=AC,∠C=65°,点D是BC边上任意一点,过点D作DF∥AB交AC于点E,则∠FEC的度数是 130° .
解:∵AB=AC,
∴∠B=∠C=65°.
∵DF∥AB,
∴∠EDC=∠B=65°.
∴∠FEC=∠C+∠EDC=130°.
故答案为:130°.
15.如图,在矩形纸片ABCD中,AB=1,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠BCA,则AC的长是 2 .
解:由翻折变换可知,AB=AF,∠B=∠AFE=90°,∠BAE=∠FAE,
∵∠EAC=∠BCA,
∴EA=EC,
∵∠AFE=90°,即EF⊥AC,
∴AF=FC=AB=1,
∴AC=2,
故答案为:2.
16.若关于x的不等式组有且只有3个整数解,则a的取值范围是 0<a≤2 .
解:,
解不等式①,得:x≥2,
解不等式②,得:x<,
∴不等式组的解集为2≤x<,
又∵不等式组有且只有三个整数解,
∴4<≤5,
解得:0<a≤2,
故答案为:0<a≤2.
17.如图,在直角坐标系中,△ABC的三个顶点的坐标分别为A(﹣6,1),B(﹣2,1),C(﹣8,3),线段DE的两个端点的坐标分别为D(﹣1,6),E(﹣1,2).若网格中有一点F,且以D,E,F为顶点的三角形与△ABC全等,则点F的坐标为 (﹣3,8)或(﹣3,0) .
解:设点F的坐标为(x,y).
∵A(﹣6,1),B(﹣2,1),C(﹣8,3),
∴AB=﹣2+6=4,AC==2,BC==2.
∵D(﹣1,6),E(﹣1,2),
∴DE=6﹣2=4,
∴DE=AB,
∴若网格中有一点F,且以D,E,F为顶点的三角形与△ABC全等,则分两种情况:
①如果△DEF≌ABC,那么EF=BC=2,DF=AC=2,
所以,解得,(不合题意舍去),
所以点F的坐标为(﹣3,8);
②如果△DEF≌BAC,那么EF=AC=2,DF=BC=2,
所以,解得,(不合题意舍去);
所以点F的坐标为(﹣3,0);
综上所述,点F的坐标为(﹣3,8)或(﹣3,0).
故答案为:(﹣3,8)或(﹣3,0).
18.如图,△ABC中,AB=AC,分别以A、B为圆心,以适当的长为半径作弧,两弧分别交于E、F,作直线EF,D为BC的中点,M为直线EF上任意一点,若BC=4,△ABC的面积为10,则BM+MD的最小值是 5 .
解:连接AD,AM,如图,
∵AB=AC,D为BC的中点,
∴AD⊥BC,
∵△ABC的面积为10,
∴×4×AD=10,解得AD=5,
由作法得EF垂直平分AB,
∴MA=MB,
∵MB+MD=MA+MD,
而MA+MD≥AD(当且仅当A、M、D共线,即M点为EF与AD的交点时取等号),
∴MA+MD的最小值为5,
∴BM+MD的最小值是5.
故答案为5.
三、解答题(本大题共6个小题,满分66分解答题要写出必要的计算步骤或文字说明或说理过程)
19.(16分)解方程组:
(1);
(2);
解不等式组:(并在数轴上表示其解集)
(3);
(4).
【解答】解;(1),
将①代入②,得11x=33,
解得x=3,
将x=3代入①,得y=3,
则方程组的解为;
(2),
①+②×4,得11x=22,
解得x=2,
将x=2代入①得y=0,
所以原解方程组的解是;
(3),
解不等式①,得x≥﹣1,
解不等式②,得x≥3,
原不等式组的解集为x≥3,
在同一数轴上表示不等式①和②的解集为:
;
(4),
解不等式①,得x<2,
解不等式②,得x≥﹣2,
原不等式组的解集为﹣2≤x<2,
在同一数轴上表示不等式组的解集为:
.
20.如图,在平面直角坐标系中,直线y=﹣x﹣1与直线y=﹣2x+2相交于点P,并分别与x轴相交于点A、B.
(1)求交点P的坐标;
(2)求△PAB的面积;
(3)请把图象中直线y=﹣2x+2在直线y=﹣x﹣1上方的部分描黑加粗,并写出此时自变量x的取值范围.
解:(1)由解得,
∴P(2,﹣2);
(2)直线y=﹣x﹣1与直线y=﹣2x+2中,令y=0,则﹣x﹣1=0与﹣2x+2=0,
解得x=﹣2与x=1,
∴A(﹣2,0),B(1,0),
∴AB=3,
∴S△PAB===3;
(3)如图所示:
自变量x的取值范围是x<2.
21.如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数.
解:∵EF∥GH,
∴∠ABD+∠FAC=180°,
∴∠ABD=180°﹣72°=108°,
∵∠ABD=∠ACD+∠BDC,
∴∠BDC=∠ABD﹣∠ACD=108°﹣58°=50°.
22.某商场为了吸引顾客,设立了一个翻奖牌(表1中的奖牌对应的奖品一种排法如表2,其中钱数为购物券),并规定:顾客购买不少于200元的商品,就能获得一次翻牌的机会.甲顾客购物220元.
表1:
1 2 3
4 5 6
7 8 9
表2:
20元 50元 谢谢参与
100元 20元 50元
20元 20元 20元
(1)甲顾客得到100元购物券的概率是多少?她获得购物券的概率是多少?
(2)请你根据本题题意写出一个事件,使这个事件发生的概率为.
解:(1)甲顾客购物220元,获得一次翻牌的机会,
所以,P(甲顾客得到100元购物券)=,
P(甲顾客得到购物券)=;
(2)答案不唯一,如:甲顾客一次翻牌得到购物券钱数不少于50元.
23.A,B两地相距200千米.早上8:00货车甲从A地出发将一批物资运往B地,行驶一段路程后出现故障,即刻停车与B地联系.B地收到消息后立即派货车乙从B地出发去接运甲车上的物资.货车乙遇到甲后,用了18分钟将物资从货车甲搬运到货车乙上,随后开往B地.两辆货车离开各自出发地的路程y(千米)与时间x(小时)的函数关系如图所示.(通话等其他时间忽略不计)
(1)求货车乙在遇到货车甲前,它离开出发地的路程y关于x的函数表达式.
(2)因实际需要,要求货车乙到达B地的时间比货车甲按原来的速度正常到达B地的时间最多晚1个小时,问货车乙返回B地的速度至少为每小时多少千米?
解:(1)设函数表达式为y=kx+b(k≠0),
把(1.6,0),(2.6,80)代入y=kx+b,得,
解得:,
∴y关于x的函数表达式为y=80x﹣128;
由图可知200﹣80=120(千米),120÷80=1.5(小时),1.6+1.5=3.1(小时),
∴x的取值范围是1.6≤x<3.1.
∴货车乙在遇到货车甲前,它离开出发地的路程y关于x的函数表达式为y=80x﹣128(1.6≤x<3.1);
(2)当y=200﹣80=120时,
120=80x﹣128,
解得x=3.1,
由图可知,甲的速度为=50(千米/小时),
货车甲正常到达B地的时间为200÷50=4(小时),
18÷60=0.3(小时),4+1=5(小时),5﹣3.1﹣0.3=1.6(小时),
设货车乙返回B地的车速为v千米/小时,
∴1.6v≥120,
解得v≥75.
答:货车乙返回B地的车速至少为75千米/小时.
24.某中学为了庆祝“建党一百周年”,计划举行阳光体育运动比赛,决定让各班购买跳绳和毽子作为活动器材.已知购买2根跳绳和5个毽子共需32元;购买4根跳绳和3个毽子共需36元.
(1)求购买一根跳绳和一个毽子分别需要多少元?
(2)某班需要购买跳绳和毽子的总数量是54,且购买的总费用不能超过260元;若要求购买跳绳的数量多于20根,通过计算说明共有哪几种购买跳绳的方案.
解:(1)设购买一根跳绳需要x元,一个毽子需要y元,
依题意得:,
解得:.
答:购买一根跳绳需要6元,一个毽子需要4元.
(2)设购买m根跳绳,则购买(54﹣m)个毽子,
依题意得:,
解得:20<m≤22,
又∵m为正整数,
∴m可以为21,22,
∴共有2种购买方案,
方案1:购买21根跳绳,33个毽子;
方案2:购买22根跳绳,32个毽子.
四、附加题(本大题共2个题.满分30分本题要写出必要的计算步骤或文字说明或说理过程)
25.如图,△ABC和△DCE都是等边三角形.
(1)△BCD与△ACE是否全等?若全等,加以证明;若不全等,请说明理由.
(2)若B、C、E三点不在一条直线上,∠ADC=30°,AD=3,CD=2,求BD的长.
解:(1)全等,理由是:
∵△ABC和△DCE都是等边三角形,
∴AC=BC,DC=EC,∠ACB=∠DCE=60°,
∴∠ACB+∠ACD=∠DCE+∠ACD,
即∠BCD=∠ACE,
在△BCD和△ACE中,
,
∴△ACE≌△BCD( SAS);
(2)由(1)得:△BCD≌△ACE,
∴BD=AE,
∵△DCE是等边三角形,
∴∠CDE=60°,CD=DE=2,
∵∠ADC=30°,
∴∠ADE=∠ADC+∠CDE=30°+60°=90°,
在Rt△ADE中,AD=3,DE=2,
∴AE===,
∴BD=.
26.(16分)在Rt△ABC中,∠ACB=90°,AC=BC,D为AB的中点.
(1)如图1,E,F分别是AC,BC上的点,且AE=CF,请判断△DEF的形状,请写出证明过程.
(2)如图2,若E,F分别分别在CA,BC的延长线上,AB=CF,(1)中的结论是否仍然成立,若成立,写出完整的证明过程;若不成立,请说出理由.
解:(1)△DEF是等腰直角三角形,
如图,连接CD,
∵∠ACB=90°,
∴∠A=∠B=45°,
∵AC=BC,D为AB的中点,
∴CD⊥AB,∠FCD=∠ACD=45°,
∴∠A=∠ACD=∠FCD,
∴AD=CD,
∵AE=CF,
∴△ADE≌△CDF(SAS),
∴DE=DF,∠ADE=∠CDF,
∵∠ADE+∠CDE=90°,
∴∠CDF+∠CDE=90°,
即∠EDF=90°,
∴△DEF是等腰直角三角形;
(2)(1)中的结论仍然成立.
理由如下:如图,连接CD,
∵∠ACB=90°,AC=BC,D为AB的中点,
∴∠CAD=∠B=45°,CD⊥AB,∠ACD=∠BCD=45°,
∴∠DAE=180°﹣∠CAD=135°,∠DCF=90°+∠ACD=135°,
∴∠DAE=∠DCF,
∵∠CAD=∠ACD,
∴AD=CD,
又∵AE=CF,
∴△ADE≌△CDF(SAS),
∴DE=DF,∠ADE=∠CDF,
∵∠ADF+∠CDF=90°,
∴∠ADF+∠ADE=90°,
即∠EDF=90°,
∴△DEF是等腰直角三角形.
一、选择题(本题共12个小题,每小题3分,满分36分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的
1.已知a<b,下列式子不一定成立的是( )
A.a﹣1<b﹣1 B.﹣2a>﹣2b
C.ma>mb D.a+1<b+1
2.下列四个命题:
①两直线平行,内错角相等;
②对顶角相等;
③等腰三角形的两个底角相等;
④同角(或等角)的余角相等.
其中逆命题是真命题的是( )
A.① B.①③ C.①③④ D.①②③④
3.不等式组的解集在数轴上表示正确的是( )
A.
B.
C.
D.
4.将一把直尺和一块含30°角的直角三角板按如图所示方式摆放,其中∠CBD=90°,∠BDC=30°,若∠1=78°,则∠2的度数为( )
A.19° B.18° C.17° D.16°
5.“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动、C点固定,OC=CD=DE,点D、E可在槽中滑动.若∠BDE=75°,则∠CDE的度数是( )
A.60° B.65° C.75° D.80°
6.若关于x的不等式组的解集是x<2,则a的取值范围是( )
A.a≥2 B.a<﹣2 C.a>2 D.a≤2
7.如图,在△ABC中,AB=AC,以点C为圆心,CB长为半径画弧,交AB于点B和点D,再分别以点B,D为圆心,大于BD长为半径画弧,两弧相交于点M,作射线CM交AB于点E.若AE=2,BE=1,则EC的长度是( )
A.2 B.3 C. D.
8.如图,在3×3的正方形网格中,有三个小正方形已经涂成灰色,若再任意涂灰1个白色的小正方形(每个白色的小正方形被涂成灰色的可能性相同),使新构成灰色部分的图形是轴对称图形的概率是( )
A. B. C. D.
9.如图所示的两台天平保持平衡,已知每块枣糕的重量相等且每个蛋挞的重量也相等,则每块枣糕和每个蛋挞的重量相差( )
A.8g B.6g C.5g D.4g
10.我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知3匹小马能拉1片瓦,1匹大马能拉3片瓦,求小马,大马各有多少匹.若设小马有x匹,大马有y匹,则下列方程组中正确的是( )
A. B.
C. D.
11.数形结合是解决数学问题常用的思想方法.如图,直线y=x+5和直线y=ax+b相交于点P,根据图象可知,方程x+5=ax+b的解是( )
A.x=20 B.x=5 C.x=25 D.x=15
12.如图,已知△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=90°,BD,CE交于点F,连接AF.下列结论:①BD=CE;②BF⊥CF;③AF平分∠CAD;④∠AFE=45°.其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本题共6个小题,每小题3分,满分18分)
13.若关于x,y的方程2x|n|+3ym﹣2=0是二元一次方程,则m+n= .
14.如图,在△ABC中,AB=AC,∠C=65°,点D是BC边上任意一点,过点D作DF∥AB交AC于点E,则∠FEC的度数是 .
15.如图,在矩形纸片ABCD中,AB=1,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠BCA,则AC的长是 .
16.若关于x的不等式组有且只有3个整数解,则a的取值范围是 .
17.如图,在直角坐标系中,△ABC的三个顶点的坐标分别为A(﹣6,1),B(﹣2,1),C(﹣8,3),线段DE的两个端点的坐标分别为D(﹣1,6),E(﹣1,2).若网格中有一点F,且以D,E,F为顶点的三角形与△ABC全等,则点F的坐标为 .
18.如图,△ABC中,AB=AC,分别以A、B为圆心,以适当的长为半径作弧,两弧分别交于E、F,作直线EF,D为BC的中点,M为直线EF上任意一点,若BC=4,△ABC的面积为10,则BM+MD的最小值是 .
三、解答题(本大题共6个小题,满分66分解答题要写出必要的计算步骤或文字说明或说理过程)
19.(16分)解方程组:
(1);
(2);
解不等式组:(并在数轴上表示其解集)
(3);
(4).
20.如图,在平面直角坐标系中,直线y=﹣x﹣1与直线y=﹣2x+2相交于点P,并分别与x轴相交于点A、B.
(1)求交点P的坐标;
(2)求△PAB的面积;
(3)请把图象中直线y=﹣2x+2在直线y=﹣x﹣1上方的部分描黑加粗,并写出此时自变量x的取值范围.
21.如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数.
22.某商场为了吸引顾客,设立了一个翻奖牌(表1中的奖牌对应的奖品一种排法如表2,其中钱数为购物券),并规定:顾客购买不少于200元的商品,就能获得一次翻牌的机会.甲顾客购物220元.
表1:
1 2 3
4 5 6
7 8 9
表2:
20元 50元 谢谢参与
100元 20元 50元
20元 20元 20元
(1)甲顾客得到100元购物券的概率是多少?她获得购物券的概率是多少?
(2)请你根据本题题意写出一个事件,使这个事件发生的概率为.
23.A,B两地相距200千米.早上8:00货车甲从A地出发将一批物资运往B地,行驶一段路程后出现故障,即刻停车与B地联系.B地收到消息后立即派货车乙从B地出发去接运甲车上的物资.货车乙遇到甲后,用了18分钟将物资从货车甲搬运到货车乙上,随后开往B地.两辆货车离开各自出发地的路程y(千米)与时间x(小时)的函数关系如图所示.(通话等其他时间忽略不计)
(1)求货车乙在遇到货车甲前,它离开出发地的路程y关于x的函数表达式.
(2)因实际需要,要求货车乙到达B地的时间比货车甲按原来的速度正常到达B地的时间最多晚1个小时,问货车乙返回B地的速度至少为每小时多少千米?
24.某中学为了庆祝“建党一百周年”,计划举行阳光体育运动比赛,决定让各班购买跳绳和毽子作为活动器材.已知购买2根跳绳和5个毽子共需32元;购买4根跳绳和3个毽子共需36元.
(1)求购买一根跳绳和一个毽子分别需要多少元?
(2)某班需要购买跳绳和毽子的总数量是54,且购买的总费用不能超过260元;若要求购买跳绳的数量多于20根,通过计算说明共有哪几种购买跳绳的方案.
四、附加题(本大题共2个题.满分30分本题要写出必要的计算步骤或文字说明或说理过程)
25.如图,△ABC和△DCE都是等边三角形.
(1)△BCD与△ACE是否全等?若全等,加以证明;若不全等,请说明理由.
(2)若B、C、E三点不在一条直线上,∠ADC=30°,AD=3,CD=2,求BD的长.
26.(16分)在Rt△ABC中,∠ACB=90°,AC=BC,D为AB的中点.
(1)如图1,E,F分别是AC,BC上的点,且AE=CF,请判断△DEF的形状,请写出证明过程.
(2)如图2,若E,F分别分别在CA,BC的延长线上,AB=CF,(1)中的结论是否仍然成立,若成立,写出完整的证明过程;若不成立,请说出理由.
参考答案
一、选择题(本题共12个小题,每小题3分,满分36分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的
1.已知a<b,下列式子不一定成立的是( )
A.a﹣1<b﹣1 B.﹣2a>﹣2b
C.ma>mb D.a+1<b+1
解:A、因为a<b,则a﹣1<b﹣1,所以A选项不符合题意;
B、因为a<b,则﹣2a>﹣2b,所以B选项不符合题意;
C、因为a<b,则当m<0时,ma>mb,所以C选项符合题意;
D、因为a<b,则a<b,所以a+1<b+1,所以D选项不符合题意.
故选:C.
2.下列四个命题:
①两直线平行,内错角相等;
②对顶角相等;
③等腰三角形的两个底角相等;
④同角(或等角)的余角相等.
其中逆命题是真命题的是( )
A.① B.①③ C.①③④ D.①②③④
解:①两直线平行,内错角相等的逆命题是内错角相等,两直线平行,逆命题是真命题;
②对顶角相等的逆命题是相等的角是对顶角,逆命题是假命题;
③等腰三角形的两个底角相等的逆命题是两个角相等的三角形是等腰三角形,逆命题是真命题;
④同角(或等角)的余角相等的逆命题是如果两个的余角相等则这两个角是同角(或等角),逆命题是真命题;
故选:C.
3.不等式组的解集在数轴上表示正确的是( )
A.
B.
C.
D.
解:不等式组,
由①得:x<2,
由②得:x≥﹣1,
∴不等式组的解集为﹣1≤x<2.
表示为:
故选:A.
4.将一把直尺和一块含30°角的直角三角板按如图所示方式摆放,其中∠CBD=90°,∠BDC=30°,若∠1=78°,则∠2的度数为( )
A.19° B.18° C.17° D.16°
解:∵∠CBD=90°,∠1=78°,
∴∠DBE=180°﹣∠CBD﹣∠1=180°﹣90°﹣78°=12°,
∵直尺的两边平行,即EA∥GH,
∴∠BDF=∠DBE=12°,
∵∠BDC=30°,
∴∠2=∠BDC﹣∠BDF=30°﹣12°=18°,
故选:B.
5.“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动、C点固定,OC=CD=DE,点D、E可在槽中滑动.若∠BDE=75°,则∠CDE的度数是( )
A.60° B.65° C.75° D.80°
解:∵OC=CD=DE,
∴∠O=∠ODC,∠DCE=∠DEC,
∴∠DCE=∠O+∠ODC=2∠ODC,
∵∠O+∠OED=3∠ODC=∠BDE=75°,
∴∠ODC=25°,
∵∠CDE+∠ODC=180°﹣∠BDE=105°,
∴∠CDE=105°﹣∠ODC=80°.
故选:D.
6.若关于x的不等式组的解集是x<2,则a的取值范围是( )
A.a≥2 B.a<﹣2 C.a>2 D.a≤2
解:解不等式组,
由①可得:x<2,
由②可得:x<a,
因为关于x的不等式组的解集是x<2,
所以,a≥2,
故选:A.
7.如图,在△ABC中,AB=AC,以点C为圆心,CB长为半径画弧,交AB于点B和点D,再分别以点B,D为圆心,大于BD长为半径画弧,两弧相交于点M,作射线CM交AB于点E.若AE=2,BE=1,则EC的长度是( )
A.2 B.3 C. D.
解:由作法得CE⊥AB,则∠AEC=90°,
AC=AB=BE+AE=2+1=3,
在Rt△ACE中,CE==.
故选:D.
8.如图,在3×3的正方形网格中,有三个小正方形已经涂成灰色,若再任意涂灰1个白色的小正方形(每个白色的小正方形被涂成灰色的可能性相同),使新构成灰色部分的图形是轴对称图形的概率是( )
A. B. C. D.
解:如图所示:当1,2两个分别涂成灰色,新构成灰色部分的图形是轴对称图形,
故新构成灰色部分的图形是轴对称图形的概率是:=.
故选:D.
9.如图所示的两台天平保持平衡,已知每块枣糕的重量相等且每个蛋挞的重量也相等,则每块枣糕和每个蛋挞的重量相差( )
A.8g B.6g C.5g D.4g
解:设枣糕的重量为xg,蛋挞的重量为yg,
由题意得,
解得,
∴y﹣x=12﹣8=4(g),
故选:D.
10.我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知3匹小马能拉1片瓦,1匹大马能拉3片瓦,求小马,大马各有多少匹.若设小马有x匹,大马有y匹,则下列方程组中正确的是( )
A. B.
C. D.
解:根据题意可得:,
故选:C.
11.数形结合是解决数学问题常用的思想方法.如图,直线y=x+5和直线y=ax+b相交于点P,根据图象可知,方程x+5=ax+b的解是( )
A.x=20 B.x=5 C.x=25 D.x=15
解:∵直线y=x+5和直线y=ax+b相交于点P(20,25)
∴方程x+5=ax+b的解为x=20.
故选:A.
12.如图,已知△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=90°,BD,CE交于点F,连接AF.下列结论:①BD=CE;②BF⊥CF;③AF平分∠CAD;④∠AFE=45°.其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
解:如图,作AM⊥BD于M,AN⊥EC于N,设AD交EF于O.
∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴△BAD≌△CAE(SAS),
∴EC=BD,∠BDA=∠AEC,故①正确
∵∠DOF=∠AOE,
∴∠DFO=∠EAO=90°,
∴BD⊥EC,故②正确,
∵△BAD≌△CAE,AM⊥BD,AN⊥EC,
∴AM=AN,
∴FA平分∠EFB,
∴∠AFE=45°,故④正确,
若③成立,则∠EAF=∠BAF,
∵∠AFE=∠AFB,
∴∠AEF=∠ABD=∠ADB,推出AB=AD,由题意知,AB不一定等于AD,
所以AF不一定平分∠CAD,故③错误,
故选:C.
二、填空题(本题共6个小题,每小题3分,满分18分)
13.若关于x,y的方程2x|n|+3ym﹣2=0是二元一次方程,则m+n= 2或4 .
解:根据题意得:|n|=1,m﹣2=1,
解得:n=±1,m=3,
∴m+n=3+1=4,m+n=3﹣1=2,
∴m+n的值是2或4,
故答案为:2或4.
14.如图,在△ABC中,AB=AC,∠C=65°,点D是BC边上任意一点,过点D作DF∥AB交AC于点E,则∠FEC的度数是 130° .
解:∵AB=AC,
∴∠B=∠C=65°.
∵DF∥AB,
∴∠EDC=∠B=65°.
∴∠FEC=∠C+∠EDC=130°.
故答案为:130°.
15.如图,在矩形纸片ABCD中,AB=1,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠BCA,则AC的长是 2 .
解:由翻折变换可知,AB=AF,∠B=∠AFE=90°,∠BAE=∠FAE,
∵∠EAC=∠BCA,
∴EA=EC,
∵∠AFE=90°,即EF⊥AC,
∴AF=FC=AB=1,
∴AC=2,
故答案为:2.
16.若关于x的不等式组有且只有3个整数解,则a的取值范围是 0<a≤2 .
解:,
解不等式①,得:x≥2,
解不等式②,得:x<,
∴不等式组的解集为2≤x<,
又∵不等式组有且只有三个整数解,
∴4<≤5,
解得:0<a≤2,
故答案为:0<a≤2.
17.如图,在直角坐标系中,△ABC的三个顶点的坐标分别为A(﹣6,1),B(﹣2,1),C(﹣8,3),线段DE的两个端点的坐标分别为D(﹣1,6),E(﹣1,2).若网格中有一点F,且以D,E,F为顶点的三角形与△ABC全等,则点F的坐标为 (﹣3,8)或(﹣3,0) .
解:设点F的坐标为(x,y).
∵A(﹣6,1),B(﹣2,1),C(﹣8,3),
∴AB=﹣2+6=4,AC==2,BC==2.
∵D(﹣1,6),E(﹣1,2),
∴DE=6﹣2=4,
∴DE=AB,
∴若网格中有一点F,且以D,E,F为顶点的三角形与△ABC全等,则分两种情况:
①如果△DEF≌ABC,那么EF=BC=2,DF=AC=2,
所以,解得,(不合题意舍去),
所以点F的坐标为(﹣3,8);
②如果△DEF≌BAC,那么EF=AC=2,DF=BC=2,
所以,解得,(不合题意舍去);
所以点F的坐标为(﹣3,0);
综上所述,点F的坐标为(﹣3,8)或(﹣3,0).
故答案为:(﹣3,8)或(﹣3,0).
18.如图,△ABC中,AB=AC,分别以A、B为圆心,以适当的长为半径作弧,两弧分别交于E、F,作直线EF,D为BC的中点,M为直线EF上任意一点,若BC=4,△ABC的面积为10,则BM+MD的最小值是 5 .
解:连接AD,AM,如图,
∵AB=AC,D为BC的中点,
∴AD⊥BC,
∵△ABC的面积为10,
∴×4×AD=10,解得AD=5,
由作法得EF垂直平分AB,
∴MA=MB,
∵MB+MD=MA+MD,
而MA+MD≥AD(当且仅当A、M、D共线,即M点为EF与AD的交点时取等号),
∴MA+MD的最小值为5,
∴BM+MD的最小值是5.
故答案为5.
三、解答题(本大题共6个小题,满分66分解答题要写出必要的计算步骤或文字说明或说理过程)
19.(16分)解方程组:
(1);
(2);
解不等式组:(并在数轴上表示其解集)
(3);
(4).
【解答】解;(1),
将①代入②,得11x=33,
解得x=3,
将x=3代入①,得y=3,
则方程组的解为;
(2),
①+②×4,得11x=22,
解得x=2,
将x=2代入①得y=0,
所以原解方程组的解是;
(3),
解不等式①,得x≥﹣1,
解不等式②,得x≥3,
原不等式组的解集为x≥3,
在同一数轴上表示不等式①和②的解集为:
;
(4),
解不等式①,得x<2,
解不等式②,得x≥﹣2,
原不等式组的解集为﹣2≤x<2,
在同一数轴上表示不等式组的解集为:
.
20.如图,在平面直角坐标系中,直线y=﹣x﹣1与直线y=﹣2x+2相交于点P,并分别与x轴相交于点A、B.
(1)求交点P的坐标;
(2)求△PAB的面积;
(3)请把图象中直线y=﹣2x+2在直线y=﹣x﹣1上方的部分描黑加粗,并写出此时自变量x的取值范围.
解:(1)由解得,
∴P(2,﹣2);
(2)直线y=﹣x﹣1与直线y=﹣2x+2中,令y=0,则﹣x﹣1=0与﹣2x+2=0,
解得x=﹣2与x=1,
∴A(﹣2,0),B(1,0),
∴AB=3,
∴S△PAB===3;
(3)如图所示:
自变量x的取值范围是x<2.
21.如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数.
解:∵EF∥GH,
∴∠ABD+∠FAC=180°,
∴∠ABD=180°﹣72°=108°,
∵∠ABD=∠ACD+∠BDC,
∴∠BDC=∠ABD﹣∠ACD=108°﹣58°=50°.
22.某商场为了吸引顾客,设立了一个翻奖牌(表1中的奖牌对应的奖品一种排法如表2,其中钱数为购物券),并规定:顾客购买不少于200元的商品,就能获得一次翻牌的机会.甲顾客购物220元.
表1:
1 2 3
4 5 6
7 8 9
表2:
20元 50元 谢谢参与
100元 20元 50元
20元 20元 20元
(1)甲顾客得到100元购物券的概率是多少?她获得购物券的概率是多少?
(2)请你根据本题题意写出一个事件,使这个事件发生的概率为.
解:(1)甲顾客购物220元,获得一次翻牌的机会,
所以,P(甲顾客得到100元购物券)=,
P(甲顾客得到购物券)=;
(2)答案不唯一,如:甲顾客一次翻牌得到购物券钱数不少于50元.
23.A,B两地相距200千米.早上8:00货车甲从A地出发将一批物资运往B地,行驶一段路程后出现故障,即刻停车与B地联系.B地收到消息后立即派货车乙从B地出发去接运甲车上的物资.货车乙遇到甲后,用了18分钟将物资从货车甲搬运到货车乙上,随后开往B地.两辆货车离开各自出发地的路程y(千米)与时间x(小时)的函数关系如图所示.(通话等其他时间忽略不计)
(1)求货车乙在遇到货车甲前,它离开出发地的路程y关于x的函数表达式.
(2)因实际需要,要求货车乙到达B地的时间比货车甲按原来的速度正常到达B地的时间最多晚1个小时,问货车乙返回B地的速度至少为每小时多少千米?
解:(1)设函数表达式为y=kx+b(k≠0),
把(1.6,0),(2.6,80)代入y=kx+b,得,
解得:,
∴y关于x的函数表达式为y=80x﹣128;
由图可知200﹣80=120(千米),120÷80=1.5(小时),1.6+1.5=3.1(小时),
∴x的取值范围是1.6≤x<3.1.
∴货车乙在遇到货车甲前,它离开出发地的路程y关于x的函数表达式为y=80x﹣128(1.6≤x<3.1);
(2)当y=200﹣80=120时,
120=80x﹣128,
解得x=3.1,
由图可知,甲的速度为=50(千米/小时),
货车甲正常到达B地的时间为200÷50=4(小时),
18÷60=0.3(小时),4+1=5(小时),5﹣3.1﹣0.3=1.6(小时),
设货车乙返回B地的车速为v千米/小时,
∴1.6v≥120,
解得v≥75.
答:货车乙返回B地的车速至少为75千米/小时.
24.某中学为了庆祝“建党一百周年”,计划举行阳光体育运动比赛,决定让各班购买跳绳和毽子作为活动器材.已知购买2根跳绳和5个毽子共需32元;购买4根跳绳和3个毽子共需36元.
(1)求购买一根跳绳和一个毽子分别需要多少元?
(2)某班需要购买跳绳和毽子的总数量是54,且购买的总费用不能超过260元;若要求购买跳绳的数量多于20根,通过计算说明共有哪几种购买跳绳的方案.
解:(1)设购买一根跳绳需要x元,一个毽子需要y元,
依题意得:,
解得:.
答:购买一根跳绳需要6元,一个毽子需要4元.
(2)设购买m根跳绳,则购买(54﹣m)个毽子,
依题意得:,
解得:20<m≤22,
又∵m为正整数,
∴m可以为21,22,
∴共有2种购买方案,
方案1:购买21根跳绳,33个毽子;
方案2:购买22根跳绳,32个毽子.
四、附加题(本大题共2个题.满分30分本题要写出必要的计算步骤或文字说明或说理过程)
25.如图,△ABC和△DCE都是等边三角形.
(1)△BCD与△ACE是否全等?若全等,加以证明;若不全等,请说明理由.
(2)若B、C、E三点不在一条直线上,∠ADC=30°,AD=3,CD=2,求BD的长.
解:(1)全等,理由是:
∵△ABC和△DCE都是等边三角形,
∴AC=BC,DC=EC,∠ACB=∠DCE=60°,
∴∠ACB+∠ACD=∠DCE+∠ACD,
即∠BCD=∠ACE,
在△BCD和△ACE中,
,
∴△ACE≌△BCD( SAS);
(2)由(1)得:△BCD≌△ACE,
∴BD=AE,
∵△DCE是等边三角形,
∴∠CDE=60°,CD=DE=2,
∵∠ADC=30°,
∴∠ADE=∠ADC+∠CDE=30°+60°=90°,
在Rt△ADE中,AD=3,DE=2,
∴AE===,
∴BD=.
26.(16分)在Rt△ABC中,∠ACB=90°,AC=BC,D为AB的中点.
(1)如图1,E,F分别是AC,BC上的点,且AE=CF,请判断△DEF的形状,请写出证明过程.
(2)如图2,若E,F分别分别在CA,BC的延长线上,AB=CF,(1)中的结论是否仍然成立,若成立,写出完整的证明过程;若不成立,请说出理由.
解:(1)△DEF是等腰直角三角形,
如图,连接CD,
∵∠ACB=90°,
∴∠A=∠B=45°,
∵AC=BC,D为AB的中点,
∴CD⊥AB,∠FCD=∠ACD=45°,
∴∠A=∠ACD=∠FCD,
∴AD=CD,
∵AE=CF,
∴△ADE≌△CDF(SAS),
∴DE=DF,∠ADE=∠CDF,
∵∠ADE+∠CDE=90°,
∴∠CDF+∠CDE=90°,
即∠EDF=90°,
∴△DEF是等腰直角三角形;
(2)(1)中的结论仍然成立.
理由如下:如图,连接CD,
∵∠ACB=90°,AC=BC,D为AB的中点,
∴∠CAD=∠B=45°,CD⊥AB,∠ACD=∠BCD=45°,
∴∠DAE=180°﹣∠CAD=135°,∠DCF=90°+∠ACD=135°,
∴∠DAE=∠DCF,
∵∠CAD=∠ACD,
∴AD=CD,
又∵AE=CF,
∴△ADE≌△CDF(SAS),
∴DE=DF,∠ADE=∠CDF,
∵∠ADF+∠CDF=90°,
∴∠ADF+∠ADE=90°,
即∠EDF=90°,
∴△DEF是等腰直角三角形.
同课章节目录
