2020-2021学年黑龙江省绥化市绥棱县八年级(下)期末数学试卷(五四学制) (Word版含解析 )
文档属性
| 名称 | 2020-2021学年黑龙江省绥化市绥棱县八年级(下)期末数学试卷(五四学制) (Word版含解析 ) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 00:00:00 | ||
图片预览




文档简介
2020-2021学年黑龙江省绥化市绥棱县八年级(下)期末数学试卷(五四学制)
一.单项选择题(每小题3分,满分30分)
1.下列二次根式中,属于最简二次根式的是( )
A. B. C. D.
2.下列各图给出了变量x与y之间的函数是( )
A. B.
C. D.
3.下列计算结果正确的是( )
A.= B.3﹣=3 C.= D.=5
4.矩形的两条对角线的夹角为60度,对角线长为15,则矩形的较短边长为( )
A.12 B.10 C.7.5 D.5
5.正方形具备而菱形不具备的性质是( )
A.四条边都相等
B.四个角都是直角
C.对角线互相垂直平分
D.每条对角线平分一组对角
6.在下列以线段a,b,c的长为三边的三角形中,不能构成直角三角形的是( )
A.a=9,b=41,c=40 B.a=5,b=12,c=13
C.a:b:c=3:4:5 D.a=11,b=12,c=15
7.关于函数y=﹣x﹣2的图象,有如下说法:
①图象过点(0,2);
②图象与x轴的交点是(2,0);
③由图象可知y随x的增大而增大;
④图象不经过第一象限;
⑤图象是与y=﹣x+2平行的直线.
其中正确的说法有( )
A.5个 B.4个 C.3个 D.2个
8.已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
9.一次函数y=mx+n与y=mnx(mn≠0),在同一平面直角坐标系的图象是( )
A. B.
C. D.
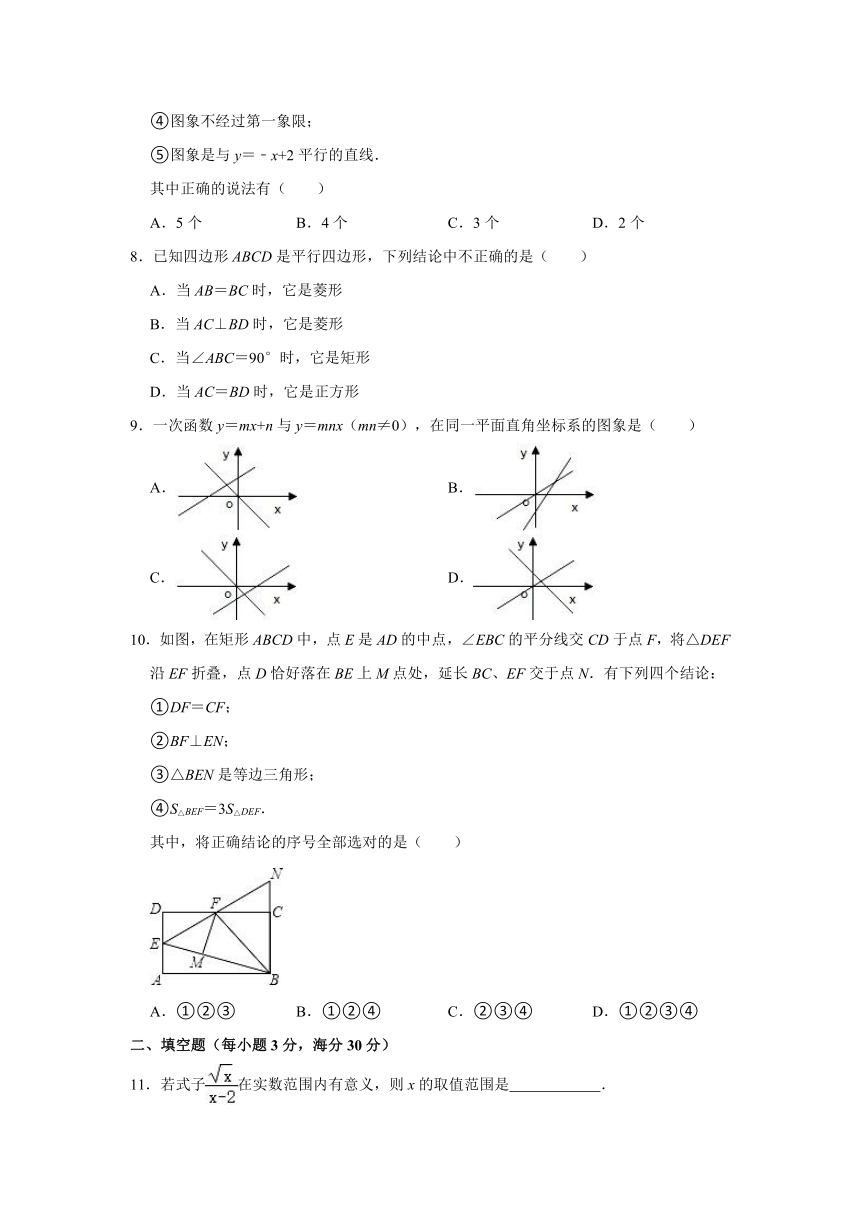
10.如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:
①DF=CF;
②BF⊥EN;
③△BEN是等边三角形;
④S△BEF=3S△DEF.
其中,将正确结论的序号全部选对的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
二、填空题(每小题3分,海分30分)
11.若式子在实数范围内有意义,则x的取值范围是 .
12.函数y=(k+1)x+(k2﹣1)是正比例函数,则k的值为 .
13.数据“1,2,1,3,3”,则这组数据的方差是 .
14.在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到斜边AB的距离是 .
15.若x,y为实数,且满足|x﹣3|+=0,则()2021的值是 .
16.已知直角三角形的两边的长分别是3和4,则第三边长为 .
17.已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值= .
18.如图,?ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,点E是BC的中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为 cm.
19.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是 .
20.在平面直角坐标系中,直线y=kx+x+1过一定点A,坐标系中有点B(2,0)和点C,要使以A、O、B、C为顶点的四边形为平行四边形,则点C的坐标为 .
三、解答题(满分60分)
21.计算:
(1)
(2).
22.当今,青少年视力水平下降已引起全社会的关注,为了了解某市3000名学生的视力情况,从中抽取了一部分学生进行了一次抽样调查,利用所得数据绘制的频数分布直方图如图,解答下列问题:
(1)本次抽样调查共抽测了 名学生;
(2)参加抽测的学生的视力的众数在 范围内;中位数在 范围内;
(3)若视力为4.9及以上为正常,试估计该市学生的视力正常的人数约为多少?
23.如图所示,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).
(1)请直接写出点B关于点A对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
24.观察下列各式及其验证过程:
验证:=;
验证:===;
验证:=;
验证:===.
(1)按照上述两个等式及其验证过程的基本思路,猜想4的变形结果并进行验证;
(2)针对上述各式反映的规律,写出用n(n为任意自然数,且n≥2)表示的等式,并给出证明.
25.甲乙两车分别从M、N两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的距离S(千米)与甲车出发时间t(小时)之间的函数图象,其中D点表示甲车到达N地,停止行驶.
(1)M、N两地的距离 千米;乙车速度是 ;a= .
(2)乙出发多长时间后两车相距330千米?
26.如图,在平行四边形ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD≌△EOC;
(2)连接AC,DE,当∠B=∠AEB= °时,四边形ACED是正方形,请说明理由.
27.甲市火车货运站现有苹果1530吨,梨1150吨,安排一列货车将这批苹果和梨运送到乙市.这列货车可以挂A、B两种不同规格的货箱共50节,已知用一节A型货箱的运费是0.5万元,用一节B型货箱的运费用是.0.8万元.
(1)设运输这批苹果和梨的总运费为y(万元),用A型货箱的节数为x(节),试写出y与x的函数关系式.
(2)已知35吨苹果和15吨梨可装满一节A型货箱,25吨苹果和35吨梨可装满一节B型车厢,请问运输所有苹果和梨的方案共有几种,请设计出来.
(3)利用函数的性质说明,在第(2)问的方案中,那种方案的运费最少,最少运费用是多少?
28.如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.
参考答案
一.单项选择题(每小题3分,满分30分)
1.下列二次根式中,属于最简二次根式的是( )
A. B. C. D.
解:A、被开方数含分母,故A错误;
B、被开方数含分母,故B错误;
C、被开方数含能开得尽方的因数,故C错误;
D、被开方数不含分母;被开方数不含能开得尽方的因数或因式,故D正确;
故选:D.
2.下列各图给出了变量x与y之间的函数是( )
A. B.
C. D.
解:A、B、C中对于x的值y的值不是唯一的,因而不符合函数的定义;
D、符合函数定义.
故选:D.
3.下列计算结果正确的是( )
A.= B.3﹣=3 C.= D.=5
解:A、原式不能合并,错误;
B、原式=2,错误;
C、原式==,正确;
D、原式=,错误,
故选:C.
4.矩形的两条对角线的夹角为60度,对角线长为15,则矩形的较短边长为( )
A.12 B.10 C.7.5 D.5
解:如下图所示:矩形ABCD,对角线AC=BD=15,∠AOD=∠BOC=60°
∵四边形ABCD是矩形
∴OA=OD=OC=OB=×15=7.5(矩形的对角线互相平分且相等)
又∵∠AOD=∠BOC=60°,
∴OA=OD=AD=7.5,
∵∠COD=120°>∠AOD=60°
∴AD<DC
所以该矩形较短的一边长为7.5,
故选:C.
5.正方形具备而菱形不具备的性质是( )
A.四条边都相等
B.四个角都是直角
C.对角线互相垂直平分
D.每条对角线平分一组对角
解:A、正方形和菱形均具有,故不正确;
B、菱形的四个角相等但不一定是直角,故正确;
C、正方形和菱形均具有此性质,故不正确;
D、正方形和菱形均具有此性质,故不正确;
故选:B.
6.在下列以线段a,b,c的长为三边的三角形中,不能构成直角三角形的是( )
A.a=9,b=41,c=40 B.a=5,b=12,c=13
C.a:b:c=3:4:5 D.a=11,b=12,c=15
解:A、因为92+402=412,能构成直角三角形,此选项错误;
B、因为52+122=132,能构成直角三角形,此选项错误;
C、因为32+42=52,故能构成直角三角形,此选项错误.
D、因为112+122≠152,不能构成直角三角形,此选项正确.
故选:D.
7.关于函数y=﹣x﹣2的图象,有如下说法:
①图象过点(0,2);
②图象与x轴的交点是(2,0);
③由图象可知y随x的增大而增大;
④图象不经过第一象限;
⑤图象是与y=﹣x+2平行的直线.
其中正确的说法有( )
A.5个 B.4个 C.3个 D.2个
解:①令x=0,则y=﹣2,
∴图象过(0,﹣2)点,正确;
②令y=0,解得x=﹣2,
∴图象与x轴交点是(﹣2,0),错误;
③∵k=﹣1<0,
∴y随x的增大而减小,错误;
④∵k<0,b=﹣2<0,
∴图象经过二、三、四象限,不经过第一象限,正确;
⑤∵y=﹣x+2与y=﹣x﹣2的k值相同,
∴图象与直线y=﹣x+2的图象平行,正确;
故选:C.
8.已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
解:
∵四边形ABCD是平行四边形,
∴当AB=BC或AC⊥BD时,四边形ABCD为菱形,故A、B结论正确;
当∠ABC=90°时,四边形ABCD为矩形,故C结论正确;
当AC=BD时,四边形ABCD为矩形,故D结论不正确,
故选:D.
9.一次函数y=mx+n与y=mnx(mn≠0),在同一平面直角坐标系的图象是( )
A. B.
C. D.
解:(1)当m>0,n>0时,mn>0,
一次函数y=mx+n的图象一、二、三象限,
正比例函数y=mnx的图象过一、三象限,无符合项;
(2)当m>0,n<0时,mn<0,
一次函数y=mx+n的图象一、三、四象限,
正比例函数y=mnx的图象过二、四象限,C选项符合;
(3)当m<0,n<0时,mn>0,
一次函数y=mx+n的图象二、三、四象限,
正比例函数y=mnx的图象过一、三象限,无符合项;
(4)当m<0,n>0时,mn<0,
一次函数y=mx+n的图象一、二、四象限,
正比例函数y=mnx的图象过二、四象限,无符合项.
故选:C.
10.如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:
①DF=CF;
②BF⊥EN;
③△BEN是等边三角形;
④S△BEF=3S△DEF.
其中,将正确结论的序号全部选对的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
解:∵四边形ABCD是矩形,
∴∠D=∠BCD=90°,DF=MF,
由折叠的性质可得:∠EMF=∠D=90°,
即FM⊥BE,CF⊥BC,
∵BF平分∠EBC,
∴CF=MF,
∴DF=CF;故①正确;
∵∠BFM=90°﹣∠EBF,∠BFC=90°﹣∠CBF,
∴∠BFM=∠BFC,
∵∠MFE=∠DFE=∠CFN,
∴∠BFE=∠BFN,
∵∠BFE+∠BFN=180°,
∴∠BFE=90°,
即BF⊥EN,故②正确;
∵在△DEF和△CNF中,
,
∴△DEF≌△CNF(ASA),
∴EF=FN,
∴BE=BN,
假设△BEN是等边三角形,则∠EBN=60°,∠EBA=30°,
则AE=BE,又∵AE=AD,则AD=BC=BE,
而明显BE=BN>BC,
∴△BEN不是等边三角形;故③错误;
∵∠BFM=∠BFC,BM⊥FM,BC⊥CF,
∴BM=BC=AD=2DE=2EM,
∴BE=3EM,
∴S△BEF=3S△EMF=3S△DEF;
故④正确.
故选:B.
二、填空题(每小题3分,海分30分)
11.若式子在实数范围内有意义,则x的取值范围是 x≥0且x≠2 .
解:根据题意得:x≥0且x﹣2≠0,
解得:x≥0且x≠2.
12.函数y=(k+1)x+(k2﹣1)是正比例函数,则k的值为 1 .
解:根据题意得:k+1≠0且k2﹣1=0,
解得:k=1.
故答案为:1.
13.数据“1,2,1,3,3”,则这组数据的方差是 0.8 .
解:数据“1,2,1,3,3”平均数==2,
S2=[(1﹣2)2+(2﹣1)2+…+(3﹣2)2]==0.8,
故答案为0.8.
14.在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到斜边AB的距离是 7.2 .
解:如图,设点C到斜边AB的距离是h,
在Rt△ABC中,∠C=90°,AC=9,BC=12,
∴AB===15,
∵S△ABC=AC?BC=AB?h,
∴h===7.2.
故答案为:7.2.
15.若x,y为实数,且满足|x﹣3|+=0,则()2021的值是 ﹣1 .
解:∵|x﹣3|+=0,
∴x﹣3=0,y+3=0,
即x=3,y=﹣3,
∴()2021=(﹣1)2021=﹣1,
故答案为:﹣1.
16.已知直角三角形的两边的长分别是3和4,则第三边长为 5或 .
解:①长为3的边是直角边,长为4的边是斜边时:
第三边的长为:=;
②长为3、4的边都是直角边时:
第三边的长为:=5;
综上,第三边的长为:5或.
故答案为:5或.
17.已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值= 5 .
解:
作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,
∵四边形ABCD是菱形,
∴AC⊥BD,∠QBP=∠MBP,
即Q在AB上,
∵MQ⊥BD,
∴AC∥MQ,
∵M为BC中点,
∴Q为AB中点,
∵N为CD中点,四边形ABCD是菱形,
∴BQ∥CD,BQ=CN,
∴四边形BQNC是平行四边形,
∴NQ=BC,
∵四边形ABCD是菱形,
∴CP=AC=3,BP=BD=4,
在Rt△BPC中,由勾股定理得:BC=5,
即NQ=5,
∴MP+NP=QP+NP=QN=5,
故答案为:5.
18.如图,?ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,点E是BC的中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为 4 cm.
解:∵?ABCD的周长为26cm,
∴AB+AD=13cm,OB=OD,
∵△AOD的周长比△AOB的周长多3cm,
∴(OA+OD+AD)﹣(OA+OB+AB)=AD﹣AB=3cm,
∴AB=5cm,AD=8cm.
∴BC=AD=8cm.
∵AC⊥AB,E是BC中点,
∴AE=BC=4cm;
故答案为:4.
19.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是 16 .
解:在矩形ABCD中,
∵AD∥BC,
∴∠DEF=∠EFB=60°,
∵把矩形ABCD沿EF翻折点B恰好落在AD边的B′处,
∴∠EFB=∠EFB′=60°,∠B=∠A′B′F=90°,∠A=∠A′=90°,AE=A′E=2,AB=A′B′,
在△EFB′中,
∵∠DEF=∠EFB=∠EB′F=60°
∴△EFB′是等边三角形,
Rt△A′EB′中,
∵∠A′B′E=90°﹣60°=30°,
∴B′E=2A′E,而A′E=2,
∴B′E=4,
∴A′B′=2,即AB=2,
∵AE=2,DE=6,
∴AD=AE+DE=2+6=8,
∴矩形ABCD的面积=AB?AD=2×8=16.
故答案为:16.
20.在平面直角坐标系中,直线y=kx+x+1过一定点A,坐标系中有点B(2,0)和点C,要使以A、O、B、C为顶点的四边形为平行四边形,则点C的坐标为 (﹣2,1),(2,﹣1)或(2,1) .
解:不论x为何值,当x=0时,一定有y=1,
则A的坐标是(0,1),
当OA是对角线时,对角线的中点是(0,),则BC的中点是(0,),设C的坐标是(x,y),
的(2+x)=0,且(0+y)=,
解得:x=﹣2,y=1,
则C的坐标是(﹣2,1);
同理,当OB是对角线时,C的坐标是(2,﹣1);
当OC是对角线时,此时AB是对角线,C的坐标是(2,1).
故答案是:(﹣2,1),(2,﹣1)或(2,1).
三、解答题(满分60分)
21.计算:
(1)
(2).
解:(1)原式=2+﹣+
=3﹣.
(2)原式=3﹣1﹣3﹣1++1
=﹣1.
22.当今,青少年视力水平下降已引起全社会的关注,为了了解某市3000名学生的视力情况,从中抽取了一部分学生进行了一次抽样调查,利用所得数据绘制的频数分布直方图如图,解答下列问题:
(1)本次抽样调查共抽测了 150 名学生;
(2)参加抽测的学生的视力的众数在 4.26~4.55 范围内;中位数在 4.26~4.55 范围内;
(3)若视力为4.9及以上为正常,试估计该市学生的视力正常的人数约为多少?
解:(1)由图表可得出:本次抽样调查共抽测了(30+50+40+20+10)=150(名)学生;
故答案为:150;
(2)∵4.26~4.55范围内的数据最多,
∴参加抽测的学生的视力的众数在4.26~4.55范围内;
∵150个数据最中间是:第75和76个数据,
∴中位数是第75和76个数据的平均数,
而第75和76个数据在4.26~4.55范围内,
∴中位数在4.26~4.55范围内;
故答案为:4.26~4.55,4.26~4.55;
(3)∵视力为4.9及以上为正常,样本中有20+10=30(人),
∴3000×=600(人),
答:该市学生的视力正常的人数约为600人.
23.如图所示,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).
(1)请直接写出点B关于点A对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
解:(1)点B关于点A对称的点的坐标为(2,6);
(2)所作图形如图所示:
,
点B'的坐标为:(0,﹣6);
(3)当以AB为对角线时,点D坐标为(﹣7,3);
当以AC为对角线时,点D坐标为(3,3);
当以BC为对角线时,点D坐标为(﹣5,﹣3).
24.观察下列各式及其验证过程:
验证:=;
验证:===;
验证:=;
验证:===.
(1)按照上述两个等式及其验证过程的基本思路,猜想4的变形结果并进行验证;
(2)针对上述各式反映的规律,写出用n(n为任意自然数,且n≥2)表示的等式,并给出证明.
解:(1).验证如下:
左边=====右边,
故猜想正确;
(2).证明如下:
左边=====右边.
25.甲乙两车分别从M、N两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的距离S(千米)与甲车出发时间t(小时)之间的函数图象,其中D点表示甲车到达N地,停止行驶.
(1)M、N两地的距离 560 千米;乙车速度是 100km/h ;a= .
(2)乙出发多长时间后两车相距330千米?
解:(1)t=0时,S=560,
所以,M、N两地的距离为560千米;
甲车的速度为:(560﹣440)÷1=120km/h,
设乙车的速度为xkm/h,
则(120+x)×(3﹣1)=440,
解得x=100;
相遇后甲车到达N地的时间为:(3﹣1)×100÷120=小时,
所以,a=(120+100)×=千米;
(2)设直线BC的解析式为S=k1t+b1(k1≠0),
将B(1,440),C(3,0)代入得,
,
解得,
所以,S=﹣220t+660,
当﹣220t+660=330时,解得t=1.5,
所以,t﹣1=1.5﹣1=0.5;
直线CD的解析式为S=k2t+b2(k2≠0),
点D的横坐标为+3=,
将C(3,0),D(,)代入得,
,
解得,
所以,S=220t﹣660(3≤t≤)
当220t﹣660=330时,解得t=4.5,
所以,t﹣1=4.5﹣1=3.5,
答:乙出发0.5小时或3.5小时后两车相距330千米.
26.如图,在平行四边形ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD≌△EOC;
(2)连接AC,DE,当∠B=∠AEB= 45 °时,四边形ACED是正方形,请说明理由.
【解答】证明:(1)∵O是CD的中点,
∴DO=CO,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠D=∠OCE,
在△ADO和△ECO中,
,
∴△AOD≌△EOC(ASA);
(2)解:当∠B=∠AEB=45°时,四边形ACED是正方形,
∵∠B=45°和∠AEB=45°,
∴∠BAE=90°,
∵△AOD≌△EOC,
∴AO=EO,
∵DO=CO,
∴四边形ACED是平行四边形,
∴AD=CE,
∵四边形ABCD是平行四边形,
∴AD=BC,
∴BC=CE,
∵∠BAE=90°,
∴AC=CE,
∴平行四边形ACED是菱形,
∵∠B=∠AEB,BC=CE,
∴AC⊥BE,
∴四边形ACED是正方形.
故答案为:45.
27.甲市火车货运站现有苹果1530吨,梨1150吨,安排一列货车将这批苹果和梨运送到乙市.这列货车可以挂A、B两种不同规格的货箱共50节,已知用一节A型货箱的运费是0.5万元,用一节B型货箱的运费用是.0.8万元.
(1)设运输这批苹果和梨的总运费为y(万元),用A型货箱的节数为x(节),试写出y与x的函数关系式.
(2)已知35吨苹果和15吨梨可装满一节A型货箱,25吨苹果和35吨梨可装满一节B型车厢,请问运输所有苹果和梨的方案共有几种,请设计出来.
(3)利用函数的性质说明,在第(2)问的方案中,那种方案的运费最少,最少运费用是多少?
解:(1)由题意得:y=0.5x+0.8(50﹣x)=﹣0.3x+40,故所求函数关系为y=﹣0.3x+40;
(2)根据题意可列不等式组
,
解得:28≤x≤30,
∴x=28,29,30,
共有3种方案.
①A28 B22
②A29 B21
③A30 B20;
(3)∵y=﹣0.3x+40,k=﹣0.3<0,
∴x值越大,y值越小,
因此方案③运费最少
当x=30时,总运费最少,即y最少=﹣0.3×30+40=31(万元).
28.如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.
解:(1)结论:PB=PQ,
理由:如图①中,过P作PE⊥BC,PF⊥CD,垂足分别为E,F.
∵P为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形.
∵∠BPE+∠QPE=90°,∠QPE+∠QPF=90°,
∴∠BPE=∠QPF,
在△PQF和△PBE中,
,
∴Rt△PQF≌Rt△PBE,
∴PB=PQ;
(2)结论:PB=PQ.
理由:如图②,过P作PE⊥BC,PF⊥CD,垂足分别为E,F,
∵P为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形,
∵∠BPF+∠QPF=90°,∠BPF+∠BPE=90°,
∴∠BPE=∠QPF,
在△PQF和△PBE中,
,
∴Rt△PQF≌Rt△PBE,
∴PB=PQ.
一.单项选择题(每小题3分,满分30分)
1.下列二次根式中,属于最简二次根式的是( )
A. B. C. D.
2.下列各图给出了变量x与y之间的函数是( )
A. B.
C. D.
3.下列计算结果正确的是( )
A.= B.3﹣=3 C.= D.=5
4.矩形的两条对角线的夹角为60度,对角线长为15,则矩形的较短边长为( )
A.12 B.10 C.7.5 D.5
5.正方形具备而菱形不具备的性质是( )
A.四条边都相等
B.四个角都是直角
C.对角线互相垂直平分
D.每条对角线平分一组对角
6.在下列以线段a,b,c的长为三边的三角形中,不能构成直角三角形的是( )
A.a=9,b=41,c=40 B.a=5,b=12,c=13
C.a:b:c=3:4:5 D.a=11,b=12,c=15
7.关于函数y=﹣x﹣2的图象,有如下说法:
①图象过点(0,2);
②图象与x轴的交点是(2,0);
③由图象可知y随x的增大而增大;
④图象不经过第一象限;
⑤图象是与y=﹣x+2平行的直线.
其中正确的说法有( )
A.5个 B.4个 C.3个 D.2个
8.已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
9.一次函数y=mx+n与y=mnx(mn≠0),在同一平面直角坐标系的图象是( )
A. B.
C. D.
10.如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:
①DF=CF;
②BF⊥EN;
③△BEN是等边三角形;
④S△BEF=3S△DEF.
其中,将正确结论的序号全部选对的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
二、填空题(每小题3分,海分30分)
11.若式子在实数范围内有意义,则x的取值范围是 .
12.函数y=(k+1)x+(k2﹣1)是正比例函数,则k的值为 .
13.数据“1,2,1,3,3”,则这组数据的方差是 .
14.在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到斜边AB的距离是 .
15.若x,y为实数,且满足|x﹣3|+=0,则()2021的值是 .
16.已知直角三角形的两边的长分别是3和4,则第三边长为 .
17.已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值= .
18.如图,?ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,点E是BC的中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为 cm.
19.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是 .
20.在平面直角坐标系中,直线y=kx+x+1过一定点A,坐标系中有点B(2,0)和点C,要使以A、O、B、C为顶点的四边形为平行四边形,则点C的坐标为 .
三、解答题(满分60分)
21.计算:
(1)
(2).
22.当今,青少年视力水平下降已引起全社会的关注,为了了解某市3000名学生的视力情况,从中抽取了一部分学生进行了一次抽样调查,利用所得数据绘制的频数分布直方图如图,解答下列问题:
(1)本次抽样调查共抽测了 名学生;
(2)参加抽测的学生的视力的众数在 范围内;中位数在 范围内;
(3)若视力为4.9及以上为正常,试估计该市学生的视力正常的人数约为多少?
23.如图所示,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).
(1)请直接写出点B关于点A对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
24.观察下列各式及其验证过程:
验证:=;
验证:===;
验证:=;
验证:===.
(1)按照上述两个等式及其验证过程的基本思路,猜想4的变形结果并进行验证;
(2)针对上述各式反映的规律,写出用n(n为任意自然数,且n≥2)表示的等式,并给出证明.
25.甲乙两车分别从M、N两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的距离S(千米)与甲车出发时间t(小时)之间的函数图象,其中D点表示甲车到达N地,停止行驶.
(1)M、N两地的距离 千米;乙车速度是 ;a= .
(2)乙出发多长时间后两车相距330千米?
26.如图,在平行四边形ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD≌△EOC;
(2)连接AC,DE,当∠B=∠AEB= °时,四边形ACED是正方形,请说明理由.
27.甲市火车货运站现有苹果1530吨,梨1150吨,安排一列货车将这批苹果和梨运送到乙市.这列货车可以挂A、B两种不同规格的货箱共50节,已知用一节A型货箱的运费是0.5万元,用一节B型货箱的运费用是.0.8万元.
(1)设运输这批苹果和梨的总运费为y(万元),用A型货箱的节数为x(节),试写出y与x的函数关系式.
(2)已知35吨苹果和15吨梨可装满一节A型货箱,25吨苹果和35吨梨可装满一节B型车厢,请问运输所有苹果和梨的方案共有几种,请设计出来.
(3)利用函数的性质说明,在第(2)问的方案中,那种方案的运费最少,最少运费用是多少?
28.如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.
参考答案
一.单项选择题(每小题3分,满分30分)
1.下列二次根式中,属于最简二次根式的是( )
A. B. C. D.
解:A、被开方数含分母,故A错误;
B、被开方数含分母,故B错误;
C、被开方数含能开得尽方的因数,故C错误;
D、被开方数不含分母;被开方数不含能开得尽方的因数或因式,故D正确;
故选:D.
2.下列各图给出了变量x与y之间的函数是( )
A. B.
C. D.
解:A、B、C中对于x的值y的值不是唯一的,因而不符合函数的定义;
D、符合函数定义.
故选:D.
3.下列计算结果正确的是( )
A.= B.3﹣=3 C.= D.=5
解:A、原式不能合并,错误;
B、原式=2,错误;
C、原式==,正确;
D、原式=,错误,
故选:C.
4.矩形的两条对角线的夹角为60度,对角线长为15,则矩形的较短边长为( )
A.12 B.10 C.7.5 D.5
解:如下图所示:矩形ABCD,对角线AC=BD=15,∠AOD=∠BOC=60°
∵四边形ABCD是矩形
∴OA=OD=OC=OB=×15=7.5(矩形的对角线互相平分且相等)
又∵∠AOD=∠BOC=60°,
∴OA=OD=AD=7.5,
∵∠COD=120°>∠AOD=60°
∴AD<DC
所以该矩形较短的一边长为7.5,
故选:C.
5.正方形具备而菱形不具备的性质是( )
A.四条边都相等
B.四个角都是直角
C.对角线互相垂直平分
D.每条对角线平分一组对角
解:A、正方形和菱形均具有,故不正确;
B、菱形的四个角相等但不一定是直角,故正确;
C、正方形和菱形均具有此性质,故不正确;
D、正方形和菱形均具有此性质,故不正确;
故选:B.
6.在下列以线段a,b,c的长为三边的三角形中,不能构成直角三角形的是( )
A.a=9,b=41,c=40 B.a=5,b=12,c=13
C.a:b:c=3:4:5 D.a=11,b=12,c=15
解:A、因为92+402=412,能构成直角三角形,此选项错误;
B、因为52+122=132,能构成直角三角形,此选项错误;
C、因为32+42=52,故能构成直角三角形,此选项错误.
D、因为112+122≠152,不能构成直角三角形,此选项正确.
故选:D.
7.关于函数y=﹣x﹣2的图象,有如下说法:
①图象过点(0,2);
②图象与x轴的交点是(2,0);
③由图象可知y随x的增大而增大;
④图象不经过第一象限;
⑤图象是与y=﹣x+2平行的直线.
其中正确的说法有( )
A.5个 B.4个 C.3个 D.2个
解:①令x=0,则y=﹣2,
∴图象过(0,﹣2)点,正确;
②令y=0,解得x=﹣2,
∴图象与x轴交点是(﹣2,0),错误;
③∵k=﹣1<0,
∴y随x的增大而减小,错误;
④∵k<0,b=﹣2<0,
∴图象经过二、三、四象限,不经过第一象限,正确;
⑤∵y=﹣x+2与y=﹣x﹣2的k值相同,
∴图象与直线y=﹣x+2的图象平行,正确;
故选:C.
8.已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
解:
∵四边形ABCD是平行四边形,
∴当AB=BC或AC⊥BD时,四边形ABCD为菱形,故A、B结论正确;
当∠ABC=90°时,四边形ABCD为矩形,故C结论正确;
当AC=BD时,四边形ABCD为矩形,故D结论不正确,
故选:D.
9.一次函数y=mx+n与y=mnx(mn≠0),在同一平面直角坐标系的图象是( )
A. B.
C. D.
解:(1)当m>0,n>0时,mn>0,
一次函数y=mx+n的图象一、二、三象限,
正比例函数y=mnx的图象过一、三象限,无符合项;
(2)当m>0,n<0时,mn<0,
一次函数y=mx+n的图象一、三、四象限,
正比例函数y=mnx的图象过二、四象限,C选项符合;
(3)当m<0,n<0时,mn>0,
一次函数y=mx+n的图象二、三、四象限,
正比例函数y=mnx的图象过一、三象限,无符合项;
(4)当m<0,n>0时,mn<0,
一次函数y=mx+n的图象一、二、四象限,
正比例函数y=mnx的图象过二、四象限,无符合项.
故选:C.
10.如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:
①DF=CF;
②BF⊥EN;
③△BEN是等边三角形;
④S△BEF=3S△DEF.
其中,将正确结论的序号全部选对的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
解:∵四边形ABCD是矩形,
∴∠D=∠BCD=90°,DF=MF,
由折叠的性质可得:∠EMF=∠D=90°,
即FM⊥BE,CF⊥BC,
∵BF平分∠EBC,
∴CF=MF,
∴DF=CF;故①正确;
∵∠BFM=90°﹣∠EBF,∠BFC=90°﹣∠CBF,
∴∠BFM=∠BFC,
∵∠MFE=∠DFE=∠CFN,
∴∠BFE=∠BFN,
∵∠BFE+∠BFN=180°,
∴∠BFE=90°,
即BF⊥EN,故②正确;
∵在△DEF和△CNF中,
,
∴△DEF≌△CNF(ASA),
∴EF=FN,
∴BE=BN,
假设△BEN是等边三角形,则∠EBN=60°,∠EBA=30°,
则AE=BE,又∵AE=AD,则AD=BC=BE,
而明显BE=BN>BC,
∴△BEN不是等边三角形;故③错误;
∵∠BFM=∠BFC,BM⊥FM,BC⊥CF,
∴BM=BC=AD=2DE=2EM,
∴BE=3EM,
∴S△BEF=3S△EMF=3S△DEF;
故④正确.
故选:B.
二、填空题(每小题3分,海分30分)
11.若式子在实数范围内有意义,则x的取值范围是 x≥0且x≠2 .
解:根据题意得:x≥0且x﹣2≠0,
解得:x≥0且x≠2.
12.函数y=(k+1)x+(k2﹣1)是正比例函数,则k的值为 1 .
解:根据题意得:k+1≠0且k2﹣1=0,
解得:k=1.
故答案为:1.
13.数据“1,2,1,3,3”,则这组数据的方差是 0.8 .
解:数据“1,2,1,3,3”平均数==2,
S2=[(1﹣2)2+(2﹣1)2+…+(3﹣2)2]==0.8,
故答案为0.8.
14.在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到斜边AB的距离是 7.2 .
解:如图,设点C到斜边AB的距离是h,
在Rt△ABC中,∠C=90°,AC=9,BC=12,
∴AB===15,
∵S△ABC=AC?BC=AB?h,
∴h===7.2.
故答案为:7.2.
15.若x,y为实数,且满足|x﹣3|+=0,则()2021的值是 ﹣1 .
解:∵|x﹣3|+=0,
∴x﹣3=0,y+3=0,
即x=3,y=﹣3,
∴()2021=(﹣1)2021=﹣1,
故答案为:﹣1.
16.已知直角三角形的两边的长分别是3和4,则第三边长为 5或 .
解:①长为3的边是直角边,长为4的边是斜边时:
第三边的长为:=;
②长为3、4的边都是直角边时:
第三边的长为:=5;
综上,第三边的长为:5或.
故答案为:5或.
17.已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值= 5 .
解:
作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,
∵四边形ABCD是菱形,
∴AC⊥BD,∠QBP=∠MBP,
即Q在AB上,
∵MQ⊥BD,
∴AC∥MQ,
∵M为BC中点,
∴Q为AB中点,
∵N为CD中点,四边形ABCD是菱形,
∴BQ∥CD,BQ=CN,
∴四边形BQNC是平行四边形,
∴NQ=BC,
∵四边形ABCD是菱形,
∴CP=AC=3,BP=BD=4,
在Rt△BPC中,由勾股定理得:BC=5,
即NQ=5,
∴MP+NP=QP+NP=QN=5,
故答案为:5.
18.如图,?ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,点E是BC的中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为 4 cm.
解:∵?ABCD的周长为26cm,
∴AB+AD=13cm,OB=OD,
∵△AOD的周长比△AOB的周长多3cm,
∴(OA+OD+AD)﹣(OA+OB+AB)=AD﹣AB=3cm,
∴AB=5cm,AD=8cm.
∴BC=AD=8cm.
∵AC⊥AB,E是BC中点,
∴AE=BC=4cm;
故答案为:4.
19.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是 16 .
解:在矩形ABCD中,
∵AD∥BC,
∴∠DEF=∠EFB=60°,
∵把矩形ABCD沿EF翻折点B恰好落在AD边的B′处,
∴∠EFB=∠EFB′=60°,∠B=∠A′B′F=90°,∠A=∠A′=90°,AE=A′E=2,AB=A′B′,
在△EFB′中,
∵∠DEF=∠EFB=∠EB′F=60°
∴△EFB′是等边三角形,
Rt△A′EB′中,
∵∠A′B′E=90°﹣60°=30°,
∴B′E=2A′E,而A′E=2,
∴B′E=4,
∴A′B′=2,即AB=2,
∵AE=2,DE=6,
∴AD=AE+DE=2+6=8,
∴矩形ABCD的面积=AB?AD=2×8=16.
故答案为:16.
20.在平面直角坐标系中,直线y=kx+x+1过一定点A,坐标系中有点B(2,0)和点C,要使以A、O、B、C为顶点的四边形为平行四边形,则点C的坐标为 (﹣2,1),(2,﹣1)或(2,1) .
解:不论x为何值,当x=0时,一定有y=1,
则A的坐标是(0,1),
当OA是对角线时,对角线的中点是(0,),则BC的中点是(0,),设C的坐标是(x,y),
的(2+x)=0,且(0+y)=,
解得:x=﹣2,y=1,
则C的坐标是(﹣2,1);
同理,当OB是对角线时,C的坐标是(2,﹣1);
当OC是对角线时,此时AB是对角线,C的坐标是(2,1).
故答案是:(﹣2,1),(2,﹣1)或(2,1).
三、解答题(满分60分)
21.计算:
(1)
(2).
解:(1)原式=2+﹣+
=3﹣.
(2)原式=3﹣1﹣3﹣1++1
=﹣1.
22.当今,青少年视力水平下降已引起全社会的关注,为了了解某市3000名学生的视力情况,从中抽取了一部分学生进行了一次抽样调查,利用所得数据绘制的频数分布直方图如图,解答下列问题:
(1)本次抽样调查共抽测了 150 名学生;
(2)参加抽测的学生的视力的众数在 4.26~4.55 范围内;中位数在 4.26~4.55 范围内;
(3)若视力为4.9及以上为正常,试估计该市学生的视力正常的人数约为多少?
解:(1)由图表可得出:本次抽样调查共抽测了(30+50+40+20+10)=150(名)学生;
故答案为:150;
(2)∵4.26~4.55范围内的数据最多,
∴参加抽测的学生的视力的众数在4.26~4.55范围内;
∵150个数据最中间是:第75和76个数据,
∴中位数是第75和76个数据的平均数,
而第75和76个数据在4.26~4.55范围内,
∴中位数在4.26~4.55范围内;
故答案为:4.26~4.55,4.26~4.55;
(3)∵视力为4.9及以上为正常,样本中有20+10=30(人),
∴3000×=600(人),
答:该市学生的视力正常的人数约为600人.
23.如图所示,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).
(1)请直接写出点B关于点A对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
解:(1)点B关于点A对称的点的坐标为(2,6);
(2)所作图形如图所示:
,
点B'的坐标为:(0,﹣6);
(3)当以AB为对角线时,点D坐标为(﹣7,3);
当以AC为对角线时,点D坐标为(3,3);
当以BC为对角线时,点D坐标为(﹣5,﹣3).
24.观察下列各式及其验证过程:
验证:=;
验证:===;
验证:=;
验证:===.
(1)按照上述两个等式及其验证过程的基本思路,猜想4的变形结果并进行验证;
(2)针对上述各式反映的规律,写出用n(n为任意自然数,且n≥2)表示的等式,并给出证明.
解:(1).验证如下:
左边=====右边,
故猜想正确;
(2).证明如下:
左边=====右边.
25.甲乙两车分别从M、N两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的距离S(千米)与甲车出发时间t(小时)之间的函数图象,其中D点表示甲车到达N地,停止行驶.
(1)M、N两地的距离 560 千米;乙车速度是 100km/h ;a= .
(2)乙出发多长时间后两车相距330千米?
解:(1)t=0时,S=560,
所以,M、N两地的距离为560千米;
甲车的速度为:(560﹣440)÷1=120km/h,
设乙车的速度为xkm/h,
则(120+x)×(3﹣1)=440,
解得x=100;
相遇后甲车到达N地的时间为:(3﹣1)×100÷120=小时,
所以,a=(120+100)×=千米;
(2)设直线BC的解析式为S=k1t+b1(k1≠0),
将B(1,440),C(3,0)代入得,
,
解得,
所以,S=﹣220t+660,
当﹣220t+660=330时,解得t=1.5,
所以,t﹣1=1.5﹣1=0.5;
直线CD的解析式为S=k2t+b2(k2≠0),
点D的横坐标为+3=,
将C(3,0),D(,)代入得,
,
解得,
所以,S=220t﹣660(3≤t≤)
当220t﹣660=330时,解得t=4.5,
所以,t﹣1=4.5﹣1=3.5,
答:乙出发0.5小时或3.5小时后两车相距330千米.
26.如图,在平行四边形ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD≌△EOC;
(2)连接AC,DE,当∠B=∠AEB= 45 °时,四边形ACED是正方形,请说明理由.
【解答】证明:(1)∵O是CD的中点,
∴DO=CO,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠D=∠OCE,
在△ADO和△ECO中,
,
∴△AOD≌△EOC(ASA);
(2)解:当∠B=∠AEB=45°时,四边形ACED是正方形,
∵∠B=45°和∠AEB=45°,
∴∠BAE=90°,
∵△AOD≌△EOC,
∴AO=EO,
∵DO=CO,
∴四边形ACED是平行四边形,
∴AD=CE,
∵四边形ABCD是平行四边形,
∴AD=BC,
∴BC=CE,
∵∠BAE=90°,
∴AC=CE,
∴平行四边形ACED是菱形,
∵∠B=∠AEB,BC=CE,
∴AC⊥BE,
∴四边形ACED是正方形.
故答案为:45.
27.甲市火车货运站现有苹果1530吨,梨1150吨,安排一列货车将这批苹果和梨运送到乙市.这列货车可以挂A、B两种不同规格的货箱共50节,已知用一节A型货箱的运费是0.5万元,用一节B型货箱的运费用是.0.8万元.
(1)设运输这批苹果和梨的总运费为y(万元),用A型货箱的节数为x(节),试写出y与x的函数关系式.
(2)已知35吨苹果和15吨梨可装满一节A型货箱,25吨苹果和35吨梨可装满一节B型车厢,请问运输所有苹果和梨的方案共有几种,请设计出来.
(3)利用函数的性质说明,在第(2)问的方案中,那种方案的运费最少,最少运费用是多少?
解:(1)由题意得:y=0.5x+0.8(50﹣x)=﹣0.3x+40,故所求函数关系为y=﹣0.3x+40;
(2)根据题意可列不等式组
,
解得:28≤x≤30,
∴x=28,29,30,
共有3种方案.
①A28 B22
②A29 B21
③A30 B20;
(3)∵y=﹣0.3x+40,k=﹣0.3<0,
∴x值越大,y值越小,
因此方案③运费最少
当x=30时,总运费最少,即y最少=﹣0.3×30+40=31(万元).
28.如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.
解:(1)结论:PB=PQ,
理由:如图①中,过P作PE⊥BC,PF⊥CD,垂足分别为E,F.
∵P为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形.
∵∠BPE+∠QPE=90°,∠QPE+∠QPF=90°,
∴∠BPE=∠QPF,
在△PQF和△PBE中,
,
∴Rt△PQF≌Rt△PBE,
∴PB=PQ;
(2)结论:PB=PQ.
理由:如图②,过P作PE⊥BC,PF⊥CD,垂足分别为E,F,
∵P为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形,
∵∠BPF+∠QPF=90°,∠BPF+∠BPE=90°,
∴∠BPE=∠QPF,
在△PQF和△PBE中,
,
∴Rt△PQF≌Rt△PBE,
∴PB=PQ.
同课章节目录
