1.1探索勾股定理(第二课时) 课件(共20张PPT)
文档属性
| 名称 | 1.1探索勾股定理(第二课时) 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 16:37:53 | ||
图片预览



文档简介
探索勾股定理第2 课时
北师版 八年级上
合作探究
新知导入
1.上节课我们已经通过探索得到了勾股定理,请问勾股定理的内容是什么?
2.如何验证勾股定理呢 ?
据不完全统计,验证的方法有400多种,你想得到自己的方法吗?
新知讲解
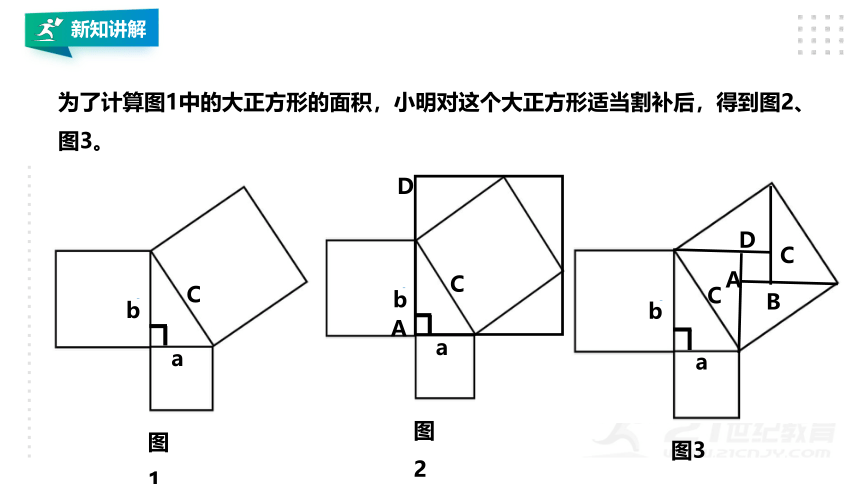
为了计算图1中的大正方形的面积,小明对这个大正方形适当割补后,得到图2、图3。
C
a
b
图1
C
a
b
图2
A
B
D
C
C
a
b
图3
A
B
C
D
做一做
(1)将所有三角形和正方形的面积用a,b,c的关系式表示出来。
(2)图2,图3中的正方形ABCD的面积分别是多少?你们有哪些表示方式?与同伴进行交流。
(3)你能分别利用图2、图3验证勾股定理吗?
新知讲解
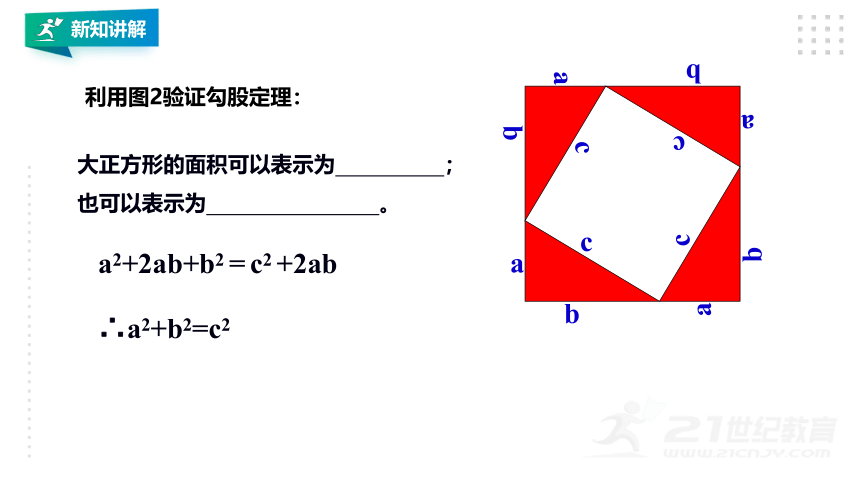
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为 。
利用图2验证勾股定理:
c
a
b
c
a
b
c
a
b
c
a
b
新知讲解
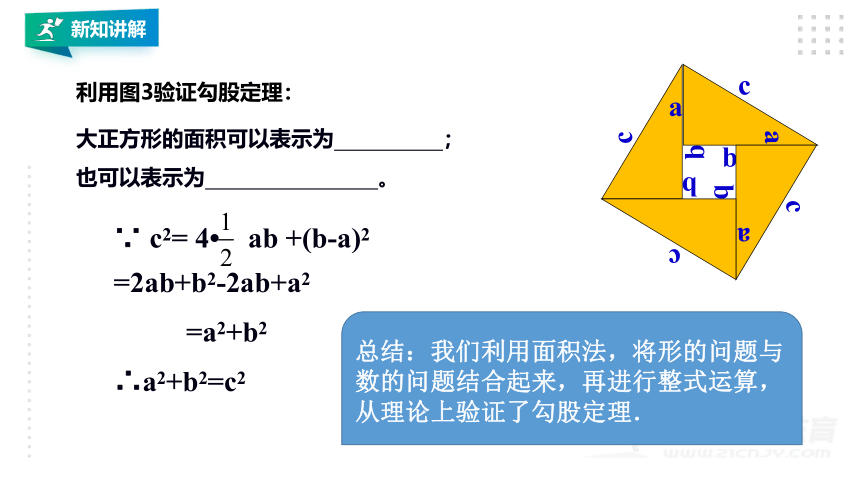
利用图3验证勾股定理:
大正方形的面积可以表示为 ;
也可以表示为 。
c
a
b
c
a
b
c
a
b
c
a
b
∵ c2= 4? ab +(b-a)2
=a2+b2
∴a2+b2=c2
=2ab+b2-2ab+a2
总结:我们利用面积法,将形的问题与数的问题结合起来,再进行整式运算,从理论上验证了勾股定理.
新知讲解
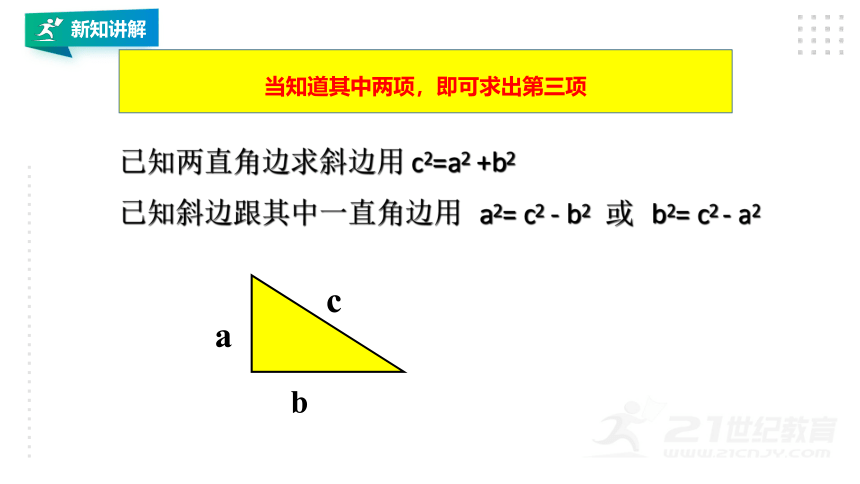
当知道其中两项,即可求出第三项
已知两直角边求斜边用 c2=a2 +b2
已知斜边跟其中一直角边用 或
b2= c2 - a2
a
b
c
a2= c2 - b2
新知讲解
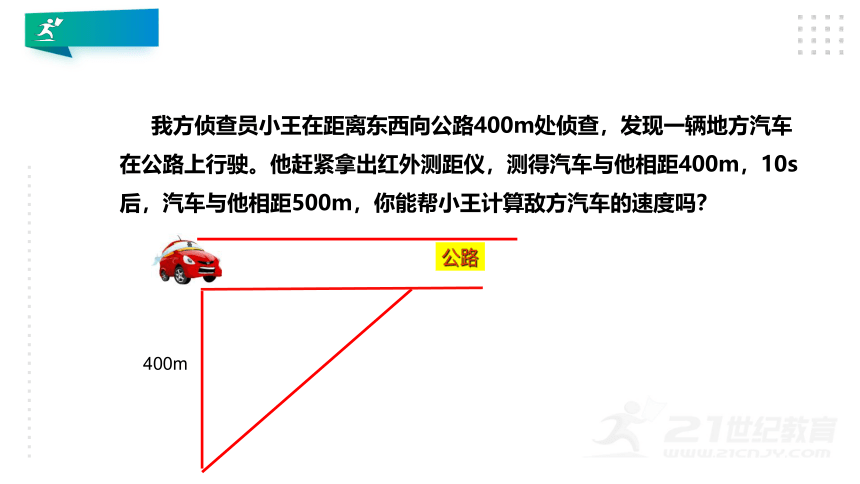
我方侦查员小王在距离东西向公路400m处侦查,发现一辆地方汽车在公路上行驶。他赶紧拿出红外测距仪,测得汽车与他相距400m,10s后,汽车与他相距500m,你能帮小王计算敌方汽车的速度吗?
400m
公路
公路
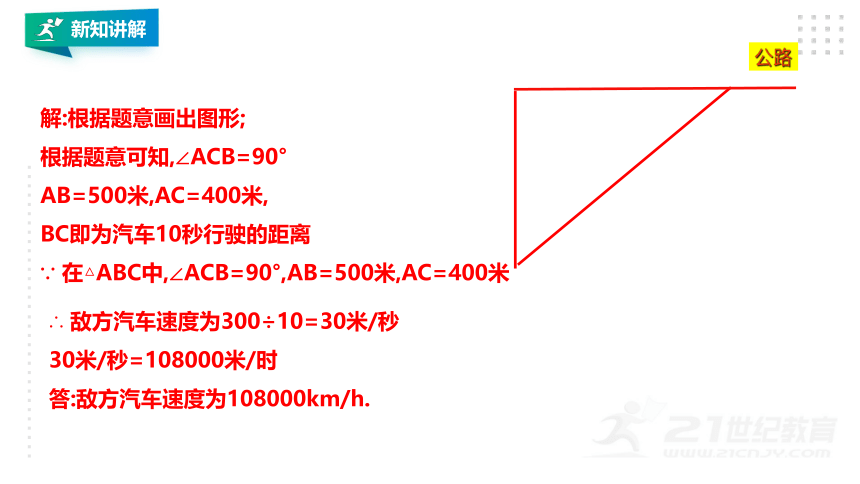
解:根据题意画出图形;
根据题意可知,∠ACB=90°
AB=500米,AC=400米,
BC即为汽车10秒行驶的距离
∵ 在△ABC中,∠ACB=90°,AB=500米,AC=400米
∴ 敌方汽车速度为300÷10=30米/秒
30米/秒=108000米/时
答:敌方汽车速度为108000km/h.
新知讲解
议一议:观察下图,用数格子的方法判断图中三角形的三边长是否满a2+b2=c2
合作探究
5
8
9
>
+
+
>
锐角三角形
钝角三角形
8
9
29
<
+
+
<
合作探究
合作探究
课堂练习
1.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )
A.0.7米 B.1.5米 C.2.2米 D.2.4米
2.在△ABC中,若∠B+∠C=90°,则( ) A.BC=AB+AC B.AC2=AB2+BC2
C.AB2=AC2+BC2 D.BC2=AB2+AC2
3.如图,字母B所代表的正方形的面积是( )
A.12 B.144 C.13 D.194
C
D
B
4.如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度至少
要( )
A.4米 B.5米 C.6米 D.7米
5.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为( )
A.3 B.4 C.5 D.6
D
C
6.如图,在Rt△ABC中,∠ACB=90°,AB=4.分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于( )
A.2π B.3π C.4π D.8π
7.《九章算术》是我国古代第一部数学专著,它的出现标志着中国古代数学形成了完整的体系.“折竹抵地”问题源自《九章算术》中:今有竹高一丈,末折抵地,去根六尺,问折高者几何?意思是一根竹子,原高一丈(一丈=10尺)一阵风将竹子折断,某竹梢恰好抵地,抵地处离竹子底部6尺远,则折断处离地面的高度是( )
A.5.3尺 B.6.8尺 C.4.7尺 D.3.2尺
B
D
8.如图,在△ABC中,CD⊥AB于点D,AC=20,CD=12,BD=9.求AB与BC的长.
【解答】解:∵CD⊥AB,AC=20,CD=12,BD=9,
∴∠ADC=∠BDC=90°,
在Rt△CDB中,
由勾股定理得:BC15,
在Rt△ADC中,
由勾股定理得:AD16,
∴AB=AD+DB=16+9=25.
答:AB的长为25,BC的长为15.
课堂总结
课堂练习
1.验证勾股定理方法
a2+b2=c2
2.勾股定理的简单应用
板书设计
课题:1.1.2探索勾股定理
一、验证勾股定理
二、勾股定理的简
单应用
?
?
例题演区
作业布置
课本P4 第4题
https://www.21cnjy.com/help/help_extract.php
北师版 八年级上
合作探究
新知导入
1.上节课我们已经通过探索得到了勾股定理,请问勾股定理的内容是什么?
2.如何验证勾股定理呢 ?
据不完全统计,验证的方法有400多种,你想得到自己的方法吗?
新知讲解
为了计算图1中的大正方形的面积,小明对这个大正方形适当割补后,得到图2、图3。
C
a
b
图1
C
a
b
图2
A
B
D
C
C
a
b
图3
A
B
C
D
做一做
(1)将所有三角形和正方形的面积用a,b,c的关系式表示出来。
(2)图2,图3中的正方形ABCD的面积分别是多少?你们有哪些表示方式?与同伴进行交流。
(3)你能分别利用图2、图3验证勾股定理吗?
新知讲解
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为 。
利用图2验证勾股定理:
c
a
b
c
a
b
c
a
b
c
a
b
新知讲解
利用图3验证勾股定理:
大正方形的面积可以表示为 ;
也可以表示为 。
c
a
b
c
a
b
c
a
b
c
a
b
∵ c2= 4? ab +(b-a)2
=a2+b2
∴a2+b2=c2
=2ab+b2-2ab+a2
总结:我们利用面积法,将形的问题与数的问题结合起来,再进行整式运算,从理论上验证了勾股定理.
新知讲解
当知道其中两项,即可求出第三项
已知两直角边求斜边用 c2=a2 +b2
已知斜边跟其中一直角边用 或
b2= c2 - a2
a
b
c
a2= c2 - b2
新知讲解
我方侦查员小王在距离东西向公路400m处侦查,发现一辆地方汽车在公路上行驶。他赶紧拿出红外测距仪,测得汽车与他相距400m,10s后,汽车与他相距500m,你能帮小王计算敌方汽车的速度吗?
400m
公路
公路
解:根据题意画出图形;
根据题意可知,∠ACB=90°
AB=500米,AC=400米,
BC即为汽车10秒行驶的距离
∵ 在△ABC中,∠ACB=90°,AB=500米,AC=400米
∴ 敌方汽车速度为300÷10=30米/秒
30米/秒=108000米/时
答:敌方汽车速度为108000km/h.
新知讲解
议一议:观察下图,用数格子的方法判断图中三角形的三边长是否满a2+b2=c2
合作探究
5
8
9
>
+
+
>
锐角三角形
钝角三角形
8
9
29
<
+
+
<
合作探究
合作探究
课堂练习
1.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )
A.0.7米 B.1.5米 C.2.2米 D.2.4米
2.在△ABC中,若∠B+∠C=90°,则( ) A.BC=AB+AC B.AC2=AB2+BC2
C.AB2=AC2+BC2 D.BC2=AB2+AC2
3.如图,字母B所代表的正方形的面积是( )
A.12 B.144 C.13 D.194
C
D
B
4.如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度至少
要( )
A.4米 B.5米 C.6米 D.7米
5.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为( )
A.3 B.4 C.5 D.6
D
C
6.如图,在Rt△ABC中,∠ACB=90°,AB=4.分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于( )
A.2π B.3π C.4π D.8π
7.《九章算术》是我国古代第一部数学专著,它的出现标志着中国古代数学形成了完整的体系.“折竹抵地”问题源自《九章算术》中:今有竹高一丈,末折抵地,去根六尺,问折高者几何?意思是一根竹子,原高一丈(一丈=10尺)一阵风将竹子折断,某竹梢恰好抵地,抵地处离竹子底部6尺远,则折断处离地面的高度是( )
A.5.3尺 B.6.8尺 C.4.7尺 D.3.2尺
B
D
8.如图,在△ABC中,CD⊥AB于点D,AC=20,CD=12,BD=9.求AB与BC的长.
【解答】解:∵CD⊥AB,AC=20,CD=12,BD=9,
∴∠ADC=∠BDC=90°,
在Rt△CDB中,
由勾股定理得:BC15,
在Rt△ADC中,
由勾股定理得:AD16,
∴AB=AD+DB=16+9=25.
答:AB的长为25,BC的长为15.
课堂总结
课堂练习
1.验证勾股定理方法
a2+b2=c2
2.勾股定理的简单应用
板书设计
课题:1.1.2探索勾股定理
一、验证勾股定理
二、勾股定理的简
单应用
?
?
例题演区
作业布置
课本P4 第4题
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
