人教版八年级上册 三角形专题知识点 典型题型 难点题型 详细答案 教案
文档属性
| 名称 | 人教版八年级上册 三角形专题知识点 典型题型 难点题型 详细答案 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 422.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-12 03:20:05 | ||
图片预览




文档简介
第十一章
三角形专题知识点+典型题型+难点题型+详细答案
第十一章
三角形专题知识点+典型题型+难点题型+详细答案
1
11.1与三角形有关的线段
2
知识框架
2
一、基础知识点
2
知识点1
认识三角形
2
知识点2
三角形三边关系
4
知识点3
三角形的高、中线与角平分线
5
知识点4
三角形的稳定性
7
二、典型题型
8
题型1
三角形三边关系(限定条件)
8
题型2
中线与三角形面积
8
题型3
高线与三角形面积
9
三、难点题型
11
题型1
与三角形有关的线段
11
题型2
面积问题—等积变换
12
11.2与三角形有关的角
15
知识框架
15
一、基础知识点
15
知识点1
三角形内角和定理
15
知识点2
三角形的外角
15
二、典型题型
17
题型1
方程思想求角度
17
题型2
转化思想求角度
17
题型3
整体思想求角度
19
题型4
数学模型—角平分线模型
20
题型5
数学模型—对顶三角形模型
20
题型6
分类讨论思想求角度
21
11.3多边形及其内角和
22
知识框架
22
一、基础知识点
22
知识点1
多边形的有关概念
22
知识点2
多边形的内角和
22
知识点3
多边形的外角和
23
二、典型题型
24
题型1
已知多边形内角和,求边
24
题型2
已知多边形的边,求内角
24
题型3
已知内、外角的关系,求边数
25
三、难点题型
26
题型1
多边形的边和角
26
11.1与三角形有关的线段
知识框架
一、基础知识点
知识点1
认识三角形
三角形定义:由不在同一条直线上的三段线段首位顺次相接所组成的图形叫作三角形。记作△ABC,读作三角形ABC。
三角形的有关概念:
①顶点:三角形两边的公共点。如:点A、点B、点C
②边:组成三角形的三条线段称为三角形的三边。如:AB(c)、BC(a)、AC(b)
③内角:在三角形中,每两条边所组成的角叫作三角形的内角。如∠CAB(∠A)、∠ABC(∠B)、∠ACB(∠C)
④对应边:∠A对应边为BC;∠B对应边为AC;∠C对应边为AB
注:当∠A不能唯一表示一个角是,必须用∠CAB表示。
三角形的分类:
①已学习,按照角分类
②还可按照边进行分类,根据边是否相等
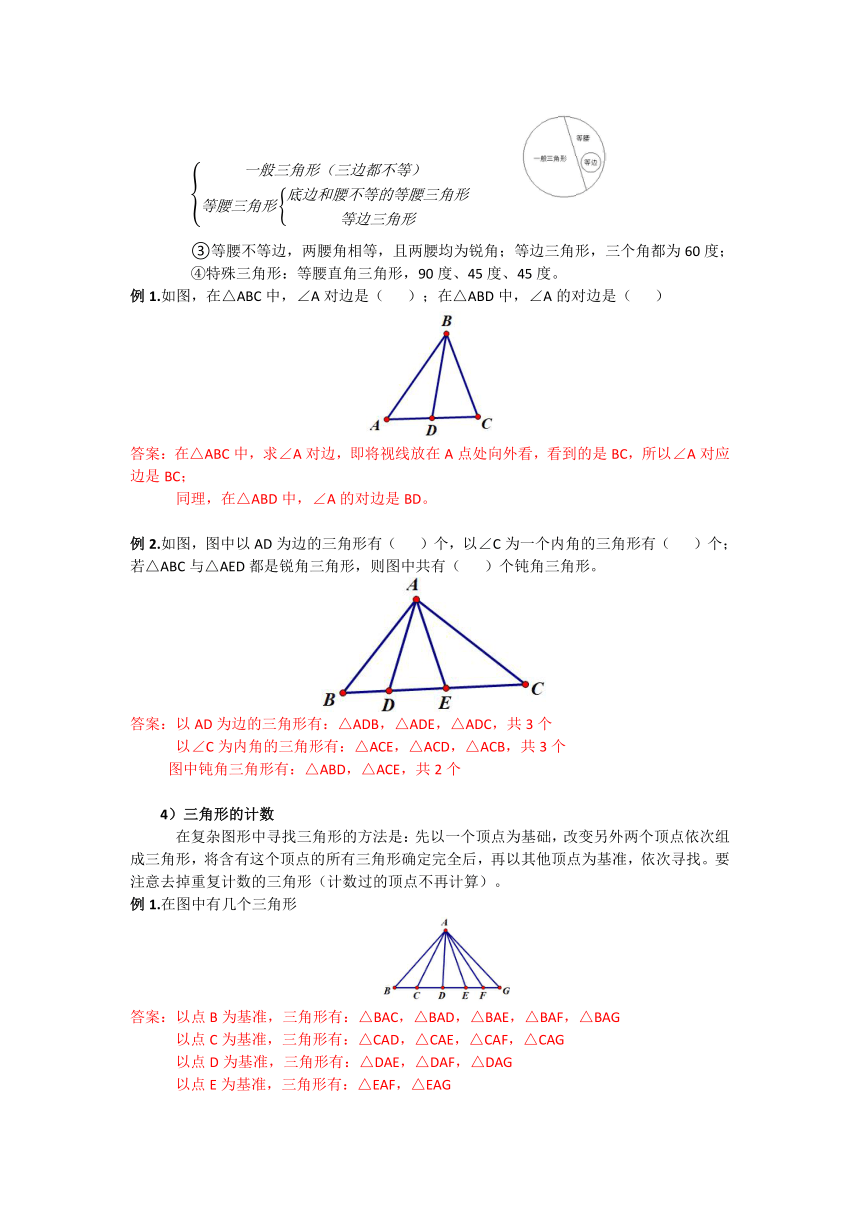
③等腰不等边,两腰角相等,且两腰均为锐角;等边三角形,三个角都为60度;④特殊三角形:等腰直角三角形,90度、45度、45度。
例1.如图,在△ABC中,∠A对边是(
);在△ABD中,∠A的对边是(
)
答案:在△ABC中,求∠A对边,即将视线放在A点处向外看,看到的是BC,所以∠A对应边是BC;
同理,在△ABD中,∠A的对边是BD。
例2.如图,图中以AD为边的三角形有(
)个,以∠C为一个内角的三角形有(
)个;若△ABC与△AED都是锐角三角形,则图中共有(
)个钝角三角形。
答案:以AD为边的三角形有:△ADB,△ADE,△ADC,共3个
以∠C为内角的三角形有:△ACE,△ACD,△ACB,共3个
图中钝角三角形有:△ABD,△ACE,共2个
4)三角形的计数
在复杂图形中寻找三角形的方法是:先以一个顶点为基础,改变另外两个顶点依次组成三角形,将含有这个顶点的所有三角形确定完全后,再以其他顶点为基准,依次寻找。要注意去掉重复计数的三角形(计数过的顶点不再计算)。
例1.在图中有几个三角形
答案:以点B为基准,三角形有:△BAC,△BAD,△BAE,△BAF,△BAG
以点C为基准,三角形有:△CAD,△CAE,△CAF,△CAG
以点D为基准,三角形有:△DAE,△DAF,△DAG
以点E为基准,三角形有:△EAF,△EAG
以点F为基准,三角形有:△FAG
因此,共有三角形15个
例2.在图中有几个三角形
答案:以点A为基准,三角形有:△ABC,△ABF,△ACD
以点B为基准,三角形有:△BCD,△BCE,△BCF,△BDE
以点C为基准,三角形有:△CEF
因此,共有三角形8个。
例3.在图中有几个三角形
答案:以点A为基准,三角形有:△ABC,△ABD,△ABE,△ACF
以点B为基准,三角形有:△BCD,△BCE,△BCF,△BCG,△BCH,△BDE,△BFG,△BFH,△BGH
以点C为基准,三角形有:△CDH,△CEG
因此,共有三角形15个
知识点2
三角形三边关系
两边之和大于第三边,两边之差小于第三边
只需满足:<第三边<两边之和(两边为相同两条边)
注:是“>”和“<”,不包含“=”
例1.三角形两边长分别为3和8,则该三角形第三边长取值范围是(
)
答案:根据三角形边长关系不等式,设第三边长为c
则8-3<c<8+3,即5<c<11
例2.下列线段能构成三角形的有哪些?
(1)6cm,8cm,10cm
(2)5cm,8cm,2cm
(3)三条线段之比为4:5:6
(4)a+1,a+2,a+3(a>0)
答案:
(1)取6cm和8cm作为两边,10cm作为第三边,判断是否符合三角形三边关系。
∵8-6<10<8+6成立
∴三边能构成三角形
(2)取5cm和8cm作为两边,2cm作为第三边,判断是否符合三角形三边关系。
∵8-5<2<8+5不成立
∴三边不能构成三角形
(3)取4和5作为两边,6作为第三边,判断是否符合三角形三边关系。
∵5-4<6<5+4成立
∴三边能构成三角形
(4)取a+1和a+2作为两边,a+3作为第三边,判断是否符合三角形三边关系。
∵(a+2)-(a+1)<a+3<(a+2)+(a+1)成立
∴三边能构成三角形
知识点3
三角形的高、中线与角平分线
三角形的高
从△ABC的顶点A向它所对应的边BC所在直线作垂线,垂足为点D。所得线段AD叫作△ABC的边BC上的高。三条高的交点叫作垂心。
注:①三角形有三个高,每条边各对应一个高
②锐角所对应边的高在三角形内,钝角对应边的高在三角形外
③三条高一定交于某一点
中线:连接△ABC的顶点A和它所对应边BC的中点D,所得线段AD叫作△ABC的边BC上的中线。三条中线的交点叫作重心。
画∠A的平分线AD,交∠A所对应的边BC于点D,线段AD叫作△ABC的角平分线。三条角平分线的交点叫作内心。
几何关系:
①垂线:AD⊥BC
②中线:CD=DB
③角平分线:∠CAD=∠DAB
例1.作下列三角形的高线。
答案:
例2.如图,在△ABC中,BD是∠ABC的角平分线,已知∠ABC=80°,求∠DBC。
答案:∵BD是∠ABC的角平分线
∴∠ABD=∠DBC
∵∠ABC=80°
∴∠DBC=∠DBA=40°
例3.如图,D、E分别是△ABC的边AC、BC的中点,则下列说法不正确的是(
)
A.DE是△BCD的中线
B.BD是△ABC的中线
C.AD=CD,BE=EC
D.∠C的对边是DE
答案:A.因为点D是AC中点,所以BD是△BAC的中线。A正确
B.因为点E是BC中点,所以DE是△DBC中线。B正确
C.因为点D、E分别是AC、BC中点,所以AD=DC,BE=EC。C正确
D.在△CDE中,∠C的对边是DE;在△BDC中,∠C的对边是BD;在△ABC中,∠C的对边是AB。D错误。
知识点4
三角形的稳定性
三角形具有稳定性(三边长度确定,形状不会改变)
多边形不稳定。要想稳定,中间加入边,构造成多个三角形
例1.下列图形具有稳定性的有(
)
A.2个
B.3个
C.4个
D.5个
答案:要想具有稳定性,则必须为三角形构成的图形
图中全部由三角形构成的图形有:第2个、第4个和第5个,共3个,选B
二、典型题型
题型1
三角形三边关系(限定条件)
性质:<第三边<两边之和
注:两边为相同两条边
解题技巧:(1)已知两条边,根据限定条件求第三条边,求解完成后,切勿忘记要验证三边是否能构成三角形。
(2)题干告知为等腰三角形,但未告知哪条边是腰时,往往有多解。最后,也需验证三边是否能构成三角形。
例1.已知等腰三角形的两边长分别是5和6,求这个等腰三角形的周长。
答案:第一种情况:等腰三角形的腰长为5,则三角形三边长为:5,5,6
验证:5-5<6<5+5成立,因此这三条边能构成等腰三角形
周长为:5+5+6=16
第二种情况:等腰三角形的腰长为6,则三角形三边长为:5,6,6
验证:6-5<6<5+6成立,因此这三条边能构成等腰三角形
周长为:5+6+6=17
例2.用一条长为36cm的细绳围成一个等腰三角形,能围成一个边长为8cm的等腰三角形吗?
答案:情况一:等腰三角形的腰长为8,则三角形三边长为:8,8,20
验证:8-8<20<8+8不成立,舍去
情况二:等腰三角形底边长为8,则三角形三边长为8,14,14
验证:14-8<14<14+8成立
综上得:可以围成一个等腰三角形,三边长分别为:8cm,14cm,14cm
例3.已知三角形三边长分别为2,8,a,且a是不等式2a-1<15的正整数解,求a的值。
答案:因为三角形三边长为2,8,a
所以8-2<a<2+8,即6<a<10
解不等式:2a-1<15得:a<8
综上得:6<a<8
所以a为7
题型2
中线与三角形面积
性质:三角形中线将三角形的面积分成相等的两部分
解题技巧:明确中线是哪个三角形的中线,这条中线将对应三角形的面积平分。题目中往往会出现多个三角形和多条中线,利用中线性质依次类推三角形的面积,直至求解出题干要求的面积。
例1.AD是△ABC的中线,AH是△ABC的高,证明中线AD将△ABC分成相等的两部分。
证明:∵
又∵AD为△ABC中线
∴BD=CD
∴
∴中线AD将△ABC分成相等的两部分
例2.
如图所示,在△ABC中,D,E,F,G分别是BC,AC,DC,EC的中点,已知△ABC的面积为1,求△FGC的面积。
答案:∵
∴
∴
∴
∴
题型3
高线与三角形面积
性质:三角形面积等于对应底边和高乘积的一半,同一个三角形面积不变
注:求面积时,底边和高必须对应
解题技巧:同一个三角形面积不变,利用这条性质,可得出等式:BC×AD=AB×CE=AC×BF。利用个等式,可求出三角形中某些不太方便求解的边。
例1.如图,已知△ABC中,AM,CN分别是△ABC对应边的高,若CN=3,AM=6,AB=10,求BC的长。
答案:∵,
又∵
∴,即×10×3=×BC×6
∴BC=5
例2.如图,AD、CE、BF分别是△ABC对应边上的高,若AB=2AC,求的值。
答案:∵,
又∵
∴
化简得:BF=2CE
∴
三、难点题型
题型1
与三角形有关的线段
性质:(1)在同一个三角形中,两边之和大于第三边,两边之差小于第三边;
(2)在同一个三角形中,大角对大边,小角对小边,等角对等边。
注:前提条件:必须在同一个三角形中
解题技巧:遇到证明边之间大小关系的题型,想办法构造三角形,将需要证明的边转化到同一个三角形中,利用性质(1)来推导证明;利用性质(2),可将同一个三角形中的角和边的关系互换。
例1.如图,△ABC中,D、E、F分别是边BC、CA、AB上的点,证明:△DEF的周长小于△ABC的周长。
证明:∵
又∵AB+BC+AC=AF+BF+BD+DC+CE+CA
∴△ABC的周长>△DEF的周长
例2.如图所示,P是△ABC内一点,连接PB、PC证明:AB+AC>PB+PC
证明:延长BP,交AB与点D
∵AB+AC=AB+AD+DC=(AB+AD)+DC
>BD+DC=BP+(PD+DC)
>BP+PC
∴AB+AC>BP+PC
例3.如图,在△ABC中有D、E两点,求证:BD+DE+EC<AB+AC
证明:延长DE,分别与AB、AC交于点F和点G
∵AB+AC=AF+FB
+CG+GA=(AF+AG)+FB+GC
>FG+
FB+GC+BC=FD+DE+EG+FB+GC+BC=(FD+FB)+(EG+GC)+DE
>BD+EC+DE
∴AB+AC>BD+DE+EC
题型2
面积问题—等积变换
性质:(1)两个三角形的面积之比等于它们的底、高乘积之比;
(2)等底(高)的两个三角形面积之比等于它们的高(底)之比;
(3)等底等高的两个三角形面积相等。
解题技巧:(1)寻找两个面积相等三角形技巧:选取底边相同的两个点的三角形,三角形的另一个顶点为与底边平行的线段上的点(等高);
(2)两图形面积之比,就是底边与高乘积之比。
注:三角形面积公式中有乘,而平行四边形中无。
例1.如图,平行四边形ABCD中,EF∥AC分别交CD、AD于E、F。连接AE、BE、BF、CF,问与△BCE面积相等的三角形还有哪些?
解:(1)在△CEB中,以CE为底边,则与CE平行线为AB
则AB上点到CE距离相等
所以△CEB与△CEA面积相等
(2)在△CEA中,以CA为底边,则与AC平行线为EF
则EF上点到AC距离相等
所以△ACE与△ACF面积相等
(3)在△ACF中,以AF为底边,则与AF平行线为BC
则BC上点到AF距离相等
所以△AFC与△AFB面积相等
综上得:与△BCE面积相等的三角形有:△ACE、△ACF、△AFB
例2.如图,D,E分别是△ABC的边AB,BC上的点,AD=2BD,BE=CE。设△ADF的面积为S1,△CEF的面积为S2,若△ABC的面积为6,求S1-S2的值。
解:∵BE=EC
∴==3
∴=3-S2,
∵,得:2S2+2(3-S1)=S1+(3-S2)
化简得:2S2+6-2S1=S1=3-S2
3=3(S1-S2)
S1-S2=1
例3.在△ABC中,E为AC中点,D在BC上,DC=2BD,AD交BE于F,
求证:S△BDF:S四边形FDCE=1:5.
证明:
设S△BDF=x,S△BAF=y
在△CDF与△DBF中,点F到边AB的距离是不变的,即△CDF与△DBF分别以CD和BD为底,则它们的高相同
∵CD:BD=2:1
∴
∴
同理,∴
∴
,∴
∴
整理得:y=3x
∴
例4.如图,已知P为△ABC内一点,AP、BP、CP分别与对边相交于点D、E、F。把△ABC分成六个小三角形,其中四个小三角形的面积已经给出。求△ABC的面积。
∵
∴,化简得:3x-4y=-112
又∵
∴,化简得:x=2y-84
解得:x=56,y=70
∴
11.2与三角形有关的角
知识框架
一、基础知识点
知识点1
三角形内角和定理
定理:三角形三个内角和等于180度
直角三角形的两个锐角互余
例1.△ABC中,若∠A=60°,∠B=65°,求∠C。
答案:因为三角形内角和为180°
所以∠C=180-60-65=55°
例2.在△ABC中,若∠A:∠B:∠C=2:3:4,求∠C。
答案:设∠A=2x,则∠B=3x,∠C=4x
则2x+3x+4x=180,解得:x=20°
所以∠C=80°
知识点2
三角形的外角
外角:三角形的一边和另一边的延长线组成的角(一个角的外角有2个)
外交性质:
性质一:三角形的外角等于它不相邻两内角和
性质二:三角形外角和相邻内角和为180度
性质三:三角形外角和为360度
例1.如图,求x的值。
答案:根据三角形外角性质:x+80=x+x+20
解得:x=60
例2.如图,已知AB∥CD,若∠C=70°,∠F=30°,求∠A的度数。
答案:∵AB∥CD,∠C=70°
∴∠FEB=70°
∵∠FEB为△AFE的外角
∴∠A+∠F=∠FEB
∵∠F=30°
∴∠A=70-30=40°
二、典型题型
题型1
方程思想求角度
性质:(1)三角形内角和=180°;
(2)对顶角相等,邻补角互补;
(3)三角形外角=不相邻两个内角和。
解题技巧:若图形中角比较多,用设未知数方法,利用上述3条性质,将图形角度之间的关系转化为方程的形式求解。
例1.在△ABC中,∠A-∠B=30°,∠C=4∠B,求∠C的度数。
答案:设∠B=x,则∠A=x+30,∠C=4x
x+30+x+4x=180
解得:x=25
∠C=4x=100°
例2.如图,△ABC中,D是BC上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠DAC的度数。
答案:设∠1=x,则∠2=x
∵∠3时△ADB外角
∴∠3=∠1+∠2=2x
∵∠3=∠4
∴∠4=2x
在△ABC中:∠2+∠4+∠BAC=180°,即x+2x+63=180
解得:x=39°
∴∠DAC=63-39=24°
例3.如图,在△ABC中,BD平分∠ABC,∠1=∠A,∠2=∠C,求∠A的度数。
答案:设∠1=x,∠2=y
根据题意得:∠1=∠DBC=∠A=x
∠2=∠C=y
在△BDC中:x+y+y=180
在△ABC中,x+x+x+y=180
解得:x=36,y=72
∴∠A=36°
题型2
转化思想求角度
解题技巧:求解多个角度和问题时,先利用三角形角度间的基本性质,将不规则图形中的角度转化到同一个三角形(多边形)中;再利用三角形(多边形)内角和性质求解角度。
例1.如图,求∠A+∠B+∠C+∠D+∠E的度数。
答案:连接BC
∵∠EFD=∠BFC
∴∠E+∠D=∠FBC+∠FCB
∴∠A+∠ABD+∠ACE+∠D+∠F=∠A+∠ABC+∠ACB=180°
例2.如图,六边形ABCDEF中,∠A=∠D,∠B=∠E,∠C=∠F,证明AF∥CD。
证明:连接CF
∵∠A=∠D,∠B=∠E
又∵四边形ABCF和四边形CDEF内角和都为360°
∴∠BCF+∠AFC=∠DCF+∠CFE
①
∵∠BCD=∠AFE
∴∠BCF+∠FCD=∠AFC+∠CFE
②
①+②得:2∠FCD+∠CFE+∠BCF=2∠AFC+∠CFE+∠BCF
∴∠FCD=∠AFC
∴AF∥CD
例3.如图,△ABC的外角平分线BP、CP交于点P,PE⊥AC于E,PF⊥AB于F,∠A=70°,求∠FPB+∠EPC的度数。
答案:设∠CBP=x,∠BCP=y,则∠FBP=x,∠PCE=y,∠ABC=180-2x,∠ACB=180-2y
在△ABC中,∠A+(180-2x)+(180-2y)=180
①
在△BCP中,x+y+∠BPC=180
②
联立①、②可得:∠BPC=90-
在四边形AEPF中,∵∠PFB=∠PEC=90°
∴∠A+∠FPE=180°,即∠A+∠FPB+∠EPC+∠BPC=180.
将∠BPC代入,化简得:90++(∠FPB+∠EPC)=180
∵∠A=70°
∴(∠FPB+∠EPC)=180-90-35=55°
题型3
整体思想求角度
解题技巧:根据题干特点,有时单一的看待某个角度,难以解出题目要求的角度。这时,需要将2个角或多个角看成一个整体,在利用三角形内角和等性质进行转化求解。
例1.如图,点D在△ABC内,且∠BDC=120°,∠1+∠2=55°,求∠A。
答案:∵∠BDC=120°
∴∠DBC+∠DCB=60°
∵∠1+∠2=55°
∴∠ABC+∠ACB=60+55=115°
∴∠A=65°
例2.如图,将△ABC沿EF折叠,使点C落在点D处,求∠1,∠2与∠C的数量关系。
答案:∵∠1+∠DEC+∠2+∠DFC=360=∠D+∠C+∠DEC+∠DFC
∴∠1+∠2=∠D+∠C
∵△AEF是△CEF折叠得到
∴∠D=∠C
∴∠1+∠2=2∠C
题型4
数学模型—角平分线模型
性质:角平分线将一个角平分为相等的两部分
解题技巧:此类题型,往往会告知多个角平分线,要求求解某一特定角。建议设平分后的角为未知数,利用方程的思想,转化为求解方程的形式来求解特定的角。
例1.已知△ABC中,点P为∠ABC和外角∠ACD的角平分线的交点,证明∠P=
证明:设∠ABP=∠PBC=x,∠PCA=∠PCD=y,∠ACB=180-2y
在△ABC中,∠A+2x+(180-2y)=180
在△BCP中,x+y+(180-2y)+∠P=180
联立化简得:∠P=90°+
例2.如图,在四边形ABCD中,AE平分∠BAD,DE平分∠ADC。
求∠B+∠C与∠AED。
答案:设∠BAE=x=∠EAD,设∠EDA=∠EDC=y
在△AED中,∠AED+x+y=180°
在四边形ABCD中,∠B+∠C+2x+2y=360°
联立化简得:∠B+∠C=2∠AED
题型5
数学模型—对顶三角形模型
性质:若两个三角形有一个对顶角,则这两个对顶角相等,那么这两个三角形剩下的两个角的和相等。
解题技巧:利用对顶三角形另两个角的和相等的性质,列写对顶三角形另两个角之和相等的等式,通过转化,求解出题干要求的角度。
例1.如图,AC,BD相交于点O,BP,CP分别平分∠ABD,∠ACD,且交于点P。若BP、CP分别为∠ABD、∠ACD的外角平分线,求∠P与∠A、∠D的关系。
答案:设∠DCP=∠PCA=x,设∠ABP=∠PBD=y
在△PCE与△AFB中:∠P+x=∠A+y
在△DCO与△ABO中:∠D+2x=∠A+2y
联立化简得:2∠P=∠A+∠D
题型6
分类讨论思想求角度
解题技巧:当题目中未出现图形时,往往有多解情况,需要分类讨论。
(1)等腰三角形中,腰和底的讨论
锐角、直角、钝角三角形高的讨论
例1.在等腰△ABC中,∠A=80°,求∠B。
答案:情况一:设等腰三角形的腰为∠A和∠B,则∠B=80°
情况二:设等腰三角形的腰为∠A和∠C,则∠A=∠C=80°,∠B=20°
情况三:设等腰三角形的腰为∠B和∠C,则∠B=∠C=50°
例2.在等腰△ABC中,∠A=60°,求∠B。
答案:情况一:设等腰三角形的腰为∠A和∠B,则∠B=60°
情况二:设等腰三角形的腰为∠A和∠C,则∠A=∠C=60°,∠B=60°
情况三:设等腰三角形的腰为∠B和∠C,则∠B=∠C=60°(重复,舍去)
例3.已知AD为△ABC的高,∠BAD=70°,∠CAD=20°,求∠BAC的度数。
答案:如图,有2种情况
情况一
情况二
情况一:∵∠BAD=70°,∠CAD=20°
∴∠CAB=70+20=90°
情况二:∵∠BAD=70°,∠CAD=20°
∴∠CAB=70-20=50°
11.3多边形及其内角和
知识框架
一、基础知识点
知识点1
多边形的有关概念
多边形:在平面内,由一些线段首位顺次连接线段组成的图形。有n条边组成,我们就称为n边形。
内角:多边形相邻两边组成的角。n边形就有n个内角
外角:多边形的边与它的邻边的延长线组成的角
对角线:连接多边形不相邻的两个顶点组成的线段。
解释:n个顶点,每个顶点不相邻顶点有(n-3)个,重复计数一次,乘
凸多边形:画出多边形的任何一条边的直线,整个多边形都在直线同一侧。反之,则叫凹多边形。
正多边形:各个角都相等,且各条边相等的多边形。
例1.下列图形中,是正多边形是的(
)
A.直角三角形
B.等腰三角形
C.长方形
D.正方形
答案:D
正多边形:每条边相等且每个角相等的多变形为正三角形
知识点2
多边形的内角和
n边形内角和为(n-2)
180
解释:n边形可分解为(n-2)个三角形,三角形内角和为180度
例1.
四边形的内角和为:
答案:180×(4-2)=360°
例2.
一个多边形的内角和是720°,则这个多边形的边数为:
答案:180×(n-2)=720
解得:n=6
例3.凸n边形的内角和为1260°,则从一个顶点出发引的对角线条数是:
答案:180×(n-2)=1260
解得:n=9
从一个顶点引发的对角线条数是:n-3=6条
知识点3
多边形的外角和
1)定理:多边形外角和为360°
注:①多边形内角和与边n有关,等于(n-2)度
②多边形外角和与边n无关,都等于360度
例1.多边形的外角和为:
答案:外角和为360°
例2.正十边形的每个外角为:
答案:无论几边形,外角和都为360°
二、典型题型
题型1
已知多边形内角和,求边
性质:多边形内角和=180(n-2)
解题技巧:利用多边形内角和公式,设边为n,列写内角和公式方程求解边n。注意理解性记忆公式,切勿强记。
例1.如果一个多边形内角和为720°,求这个多边形的边数。
答案:180×(n-2)=720
n=6
题型2
已知多边形的边,求内角
性质:多边形内角和=180(n-2)
解题技巧:先利用多边形内角和公式,将边数n代入公式求出内角和;再结合图形特点,求出提高要求的角度。
例1.如图,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,求∠3+∠1-∠2。
答案:正三角形内角为:
正四边形内角为:
正五边形内角为:
正六边形内角为:
∴∠3=90°-60°=30°
∠2=108°-90°=18°
∠1=120°-108°=12°
∴∠3+∠1-∠2=30+12-18=24°
例2.
如图,平面上两个正方形与正五边形都有一条公共边,则∠=
答案:正四边形内角为:
正五边形内角为:
根据图形得:108+90+90+a=360
得:a=72°
题型3
已知内、外角的关系,求边数
性质:(1)多边形内角和=180(n-2)
(2)多边形外角和为360度
解题技巧:设多边形边数为n,牢牢把握多边形外角和为360度这个不变量,根据题干内、外角之间的关系,列写含有n的方程,从而求解多边形边数n。
例1.一个多边形的内角和是外角和的3倍,求这个多边形的边数。
答案:设多边形边数为n
则:180×(n-2)=3×180
解得:n=5
例2.
一个多边形中各内角相等,且每个内角与外角之差的绝对值为60°,求这个多边形的边数
答案:设多边形边数为n,则内角为:
外角为:180-
根据题意,则:=60
化简得:或
解得:n=3或n=6
三、难点题型
题型1
多边形的边和角
性质:(1)多边形内角和:180(n-2);
(2)多边形外角和:360°;
(3)多边形对角线:。
解题技巧:此类题型比较灵活,要紧抓住边这个条件。无论是内角和、对角线都仅与边有关系。因此,在解决此类问题时,要想办法先求出多边形的边,在依据题目要求进行求解。在条件比较复杂情况下,可设多边形的边为未知数,转化为方程求解。
例1.如图,一个多边形纸片按图示的剪发剪去一个内角后,得到一个内角和为2340°的新多边形,求原多边形的边数?
解:如图进行剪切,多边形增加了一个边,设剪切后的边为n条
则:180(n-2)=2340
n=15
所以原多边形的边数为:n-1=15-1=14
例2.
如图,以六边形的每个顶点为圆心,1为半径画圆,则图中阴影部分的面积为:
解:6边形内角和为:180×(6-2)=720°
阴影部分面积为6个小扇形组成,它们的圆心角和为6变形内角和,为720°
根据扇形面积公式,阴影部分面积==2π
例3.在一个多边形中,除了两个内角外,其余的内角和为2002°,求这个多边形的边数。
解:设这个多边形为n,两个内角和为x
则:180(n-2)-x=2002
化简得:180n=2362+x
∵0<x<360
∴2362<2360+x<2762
∴2362<180n<2762
解得:
因为n为整数,所以n=14或n=15
三角形专题知识点+典型题型+难点题型+详细答案
第十一章
三角形专题知识点+典型题型+难点题型+详细答案
1
11.1与三角形有关的线段
2
知识框架
2
一、基础知识点
2
知识点1
认识三角形
2
知识点2
三角形三边关系
4
知识点3
三角形的高、中线与角平分线
5
知识点4
三角形的稳定性
7
二、典型题型
8
题型1
三角形三边关系(限定条件)
8
题型2
中线与三角形面积
8
题型3
高线与三角形面积
9
三、难点题型
11
题型1
与三角形有关的线段
11
题型2
面积问题—等积变换
12
11.2与三角形有关的角
15
知识框架
15
一、基础知识点
15
知识点1
三角形内角和定理
15
知识点2
三角形的外角
15
二、典型题型
17
题型1
方程思想求角度
17
题型2
转化思想求角度
17
题型3
整体思想求角度
19
题型4
数学模型—角平分线模型
20
题型5
数学模型—对顶三角形模型
20
题型6
分类讨论思想求角度
21
11.3多边形及其内角和
22
知识框架
22
一、基础知识点
22
知识点1
多边形的有关概念
22
知识点2
多边形的内角和
22
知识点3
多边形的外角和
23
二、典型题型
24
题型1
已知多边形内角和,求边
24
题型2
已知多边形的边,求内角
24
题型3
已知内、外角的关系,求边数
25
三、难点题型
26
题型1
多边形的边和角
26
11.1与三角形有关的线段
知识框架
一、基础知识点
知识点1
认识三角形
三角形定义:由不在同一条直线上的三段线段首位顺次相接所组成的图形叫作三角形。记作△ABC,读作三角形ABC。
三角形的有关概念:
①顶点:三角形两边的公共点。如:点A、点B、点C
②边:组成三角形的三条线段称为三角形的三边。如:AB(c)、BC(a)、AC(b)
③内角:在三角形中,每两条边所组成的角叫作三角形的内角。如∠CAB(∠A)、∠ABC(∠B)、∠ACB(∠C)
④对应边:∠A对应边为BC;∠B对应边为AC;∠C对应边为AB
注:当∠A不能唯一表示一个角是,必须用∠CAB表示。
三角形的分类:
①已学习,按照角分类
②还可按照边进行分类,根据边是否相等
③等腰不等边,两腰角相等,且两腰均为锐角;等边三角形,三个角都为60度;④特殊三角形:等腰直角三角形,90度、45度、45度。
例1.如图,在△ABC中,∠A对边是(
);在△ABD中,∠A的对边是(
)
答案:在△ABC中,求∠A对边,即将视线放在A点处向外看,看到的是BC,所以∠A对应边是BC;
同理,在△ABD中,∠A的对边是BD。
例2.如图,图中以AD为边的三角形有(
)个,以∠C为一个内角的三角形有(
)个;若△ABC与△AED都是锐角三角形,则图中共有(
)个钝角三角形。
答案:以AD为边的三角形有:△ADB,△ADE,△ADC,共3个
以∠C为内角的三角形有:△ACE,△ACD,△ACB,共3个
图中钝角三角形有:△ABD,△ACE,共2个
4)三角形的计数
在复杂图形中寻找三角形的方法是:先以一个顶点为基础,改变另外两个顶点依次组成三角形,将含有这个顶点的所有三角形确定完全后,再以其他顶点为基准,依次寻找。要注意去掉重复计数的三角形(计数过的顶点不再计算)。
例1.在图中有几个三角形
答案:以点B为基准,三角形有:△BAC,△BAD,△BAE,△BAF,△BAG
以点C为基准,三角形有:△CAD,△CAE,△CAF,△CAG
以点D为基准,三角形有:△DAE,△DAF,△DAG
以点E为基准,三角形有:△EAF,△EAG
以点F为基准,三角形有:△FAG
因此,共有三角形15个
例2.在图中有几个三角形
答案:以点A为基准,三角形有:△ABC,△ABF,△ACD
以点B为基准,三角形有:△BCD,△BCE,△BCF,△BDE
以点C为基准,三角形有:△CEF
因此,共有三角形8个。
例3.在图中有几个三角形
答案:以点A为基准,三角形有:△ABC,△ABD,△ABE,△ACF
以点B为基准,三角形有:△BCD,△BCE,△BCF,△BCG,△BCH,△BDE,△BFG,△BFH,△BGH
以点C为基准,三角形有:△CDH,△CEG
因此,共有三角形15个
知识点2
三角形三边关系
两边之和大于第三边,两边之差小于第三边
只需满足:<第三边<两边之和(两边为相同两条边)
注:是“>”和“<”,不包含“=”
例1.三角形两边长分别为3和8,则该三角形第三边长取值范围是(
)
答案:根据三角形边长关系不等式,设第三边长为c
则8-3<c<8+3,即5<c<11
例2.下列线段能构成三角形的有哪些?
(1)6cm,8cm,10cm
(2)5cm,8cm,2cm
(3)三条线段之比为4:5:6
(4)a+1,a+2,a+3(a>0)
答案:
(1)取6cm和8cm作为两边,10cm作为第三边,判断是否符合三角形三边关系。
∵8-6<10<8+6成立
∴三边能构成三角形
(2)取5cm和8cm作为两边,2cm作为第三边,判断是否符合三角形三边关系。
∵8-5<2<8+5不成立
∴三边不能构成三角形
(3)取4和5作为两边,6作为第三边,判断是否符合三角形三边关系。
∵5-4<6<5+4成立
∴三边能构成三角形
(4)取a+1和a+2作为两边,a+3作为第三边,判断是否符合三角形三边关系。
∵(a+2)-(a+1)<a+3<(a+2)+(a+1)成立
∴三边能构成三角形
知识点3
三角形的高、中线与角平分线
三角形的高
从△ABC的顶点A向它所对应的边BC所在直线作垂线,垂足为点D。所得线段AD叫作△ABC的边BC上的高。三条高的交点叫作垂心。
注:①三角形有三个高,每条边各对应一个高
②锐角所对应边的高在三角形内,钝角对应边的高在三角形外
③三条高一定交于某一点
中线:连接△ABC的顶点A和它所对应边BC的中点D,所得线段AD叫作△ABC的边BC上的中线。三条中线的交点叫作重心。
画∠A的平分线AD,交∠A所对应的边BC于点D,线段AD叫作△ABC的角平分线。三条角平分线的交点叫作内心。
几何关系:
①垂线:AD⊥BC
②中线:CD=DB
③角平分线:∠CAD=∠DAB
例1.作下列三角形的高线。
答案:
例2.如图,在△ABC中,BD是∠ABC的角平分线,已知∠ABC=80°,求∠DBC。
答案:∵BD是∠ABC的角平分线
∴∠ABD=∠DBC
∵∠ABC=80°
∴∠DBC=∠DBA=40°
例3.如图,D、E分别是△ABC的边AC、BC的中点,则下列说法不正确的是(
)
A.DE是△BCD的中线
B.BD是△ABC的中线
C.AD=CD,BE=EC
D.∠C的对边是DE
答案:A.因为点D是AC中点,所以BD是△BAC的中线。A正确
B.因为点E是BC中点,所以DE是△DBC中线。B正确
C.因为点D、E分别是AC、BC中点,所以AD=DC,BE=EC。C正确
D.在△CDE中,∠C的对边是DE;在△BDC中,∠C的对边是BD;在△ABC中,∠C的对边是AB。D错误。
知识点4
三角形的稳定性
三角形具有稳定性(三边长度确定,形状不会改变)
多边形不稳定。要想稳定,中间加入边,构造成多个三角形
例1.下列图形具有稳定性的有(
)
A.2个
B.3个
C.4个
D.5个
答案:要想具有稳定性,则必须为三角形构成的图形
图中全部由三角形构成的图形有:第2个、第4个和第5个,共3个,选B
二、典型题型
题型1
三角形三边关系(限定条件)
性质:<第三边<两边之和
注:两边为相同两条边
解题技巧:(1)已知两条边,根据限定条件求第三条边,求解完成后,切勿忘记要验证三边是否能构成三角形。
(2)题干告知为等腰三角形,但未告知哪条边是腰时,往往有多解。最后,也需验证三边是否能构成三角形。
例1.已知等腰三角形的两边长分别是5和6,求这个等腰三角形的周长。
答案:第一种情况:等腰三角形的腰长为5,则三角形三边长为:5,5,6
验证:5-5<6<5+5成立,因此这三条边能构成等腰三角形
周长为:5+5+6=16
第二种情况:等腰三角形的腰长为6,则三角形三边长为:5,6,6
验证:6-5<6<5+6成立,因此这三条边能构成等腰三角形
周长为:5+6+6=17
例2.用一条长为36cm的细绳围成一个等腰三角形,能围成一个边长为8cm的等腰三角形吗?
答案:情况一:等腰三角形的腰长为8,则三角形三边长为:8,8,20
验证:8-8<20<8+8不成立,舍去
情况二:等腰三角形底边长为8,则三角形三边长为8,14,14
验证:14-8<14<14+8成立
综上得:可以围成一个等腰三角形,三边长分别为:8cm,14cm,14cm
例3.已知三角形三边长分别为2,8,a,且a是不等式2a-1<15的正整数解,求a的值。
答案:因为三角形三边长为2,8,a
所以8-2<a<2+8,即6<a<10
解不等式:2a-1<15得:a<8
综上得:6<a<8
所以a为7
题型2
中线与三角形面积
性质:三角形中线将三角形的面积分成相等的两部分
解题技巧:明确中线是哪个三角形的中线,这条中线将对应三角形的面积平分。题目中往往会出现多个三角形和多条中线,利用中线性质依次类推三角形的面积,直至求解出题干要求的面积。
例1.AD是△ABC的中线,AH是△ABC的高,证明中线AD将△ABC分成相等的两部分。
证明:∵
又∵AD为△ABC中线
∴BD=CD
∴
∴中线AD将△ABC分成相等的两部分
例2.
如图所示,在△ABC中,D,E,F,G分别是BC,AC,DC,EC的中点,已知△ABC的面积为1,求△FGC的面积。
答案:∵
∴
∴
∴
∴
题型3
高线与三角形面积
性质:三角形面积等于对应底边和高乘积的一半,同一个三角形面积不变
注:求面积时,底边和高必须对应
解题技巧:同一个三角形面积不变,利用这条性质,可得出等式:BC×AD=AB×CE=AC×BF。利用个等式,可求出三角形中某些不太方便求解的边。
例1.如图,已知△ABC中,AM,CN分别是△ABC对应边的高,若CN=3,AM=6,AB=10,求BC的长。
答案:∵,
又∵
∴,即×10×3=×BC×6
∴BC=5
例2.如图,AD、CE、BF分别是△ABC对应边上的高,若AB=2AC,求的值。
答案:∵,
又∵
∴
化简得:BF=2CE
∴
三、难点题型
题型1
与三角形有关的线段
性质:(1)在同一个三角形中,两边之和大于第三边,两边之差小于第三边;
(2)在同一个三角形中,大角对大边,小角对小边,等角对等边。
注:前提条件:必须在同一个三角形中
解题技巧:遇到证明边之间大小关系的题型,想办法构造三角形,将需要证明的边转化到同一个三角形中,利用性质(1)来推导证明;利用性质(2),可将同一个三角形中的角和边的关系互换。
例1.如图,△ABC中,D、E、F分别是边BC、CA、AB上的点,证明:△DEF的周长小于△ABC的周长。
证明:∵
又∵AB+BC+AC=AF+BF+BD+DC+CE+CA
∴△ABC的周长>△DEF的周长
例2.如图所示,P是△ABC内一点,连接PB、PC证明:AB+AC>PB+PC
证明:延长BP,交AB与点D
∵AB+AC=AB+AD+DC=(AB+AD)+DC
>BD+DC=BP+(PD+DC)
>BP+PC
∴AB+AC>BP+PC
例3.如图,在△ABC中有D、E两点,求证:BD+DE+EC<AB+AC
证明:延长DE,分别与AB、AC交于点F和点G
∵AB+AC=AF+FB
+CG+GA=(AF+AG)+FB+GC
>FG+
FB+GC+BC=FD+DE+EG+FB+GC+BC=(FD+FB)+(EG+GC)+DE
>BD+EC+DE
∴AB+AC>BD+DE+EC
题型2
面积问题—等积变换
性质:(1)两个三角形的面积之比等于它们的底、高乘积之比;
(2)等底(高)的两个三角形面积之比等于它们的高(底)之比;
(3)等底等高的两个三角形面积相等。
解题技巧:(1)寻找两个面积相等三角形技巧:选取底边相同的两个点的三角形,三角形的另一个顶点为与底边平行的线段上的点(等高);
(2)两图形面积之比,就是底边与高乘积之比。
注:三角形面积公式中有乘,而平行四边形中无。
例1.如图,平行四边形ABCD中,EF∥AC分别交CD、AD于E、F。连接AE、BE、BF、CF,问与△BCE面积相等的三角形还有哪些?
解:(1)在△CEB中,以CE为底边,则与CE平行线为AB
则AB上点到CE距离相等
所以△CEB与△CEA面积相等
(2)在△CEA中,以CA为底边,则与AC平行线为EF
则EF上点到AC距离相等
所以△ACE与△ACF面积相等
(3)在△ACF中,以AF为底边,则与AF平行线为BC
则BC上点到AF距离相等
所以△AFC与△AFB面积相等
综上得:与△BCE面积相等的三角形有:△ACE、△ACF、△AFB
例2.如图,D,E分别是△ABC的边AB,BC上的点,AD=2BD,BE=CE。设△ADF的面积为S1,△CEF的面积为S2,若△ABC的面积为6,求S1-S2的值。
解:∵BE=EC
∴==3
∴=3-S2,
∵,得:2S2+2(3-S1)=S1+(3-S2)
化简得:2S2+6-2S1=S1=3-S2
3=3(S1-S2)
S1-S2=1
例3.在△ABC中,E为AC中点,D在BC上,DC=2BD,AD交BE于F,
求证:S△BDF:S四边形FDCE=1:5.
证明:
设S△BDF=x,S△BAF=y
在△CDF与△DBF中,点F到边AB的距离是不变的,即△CDF与△DBF分别以CD和BD为底,则它们的高相同
∵CD:BD=2:1
∴
∴
同理,∴
∴
,∴
∴
整理得:y=3x
∴
例4.如图,已知P为△ABC内一点,AP、BP、CP分别与对边相交于点D、E、F。把△ABC分成六个小三角形,其中四个小三角形的面积已经给出。求△ABC的面积。
∵
∴,化简得:3x-4y=-112
又∵
∴,化简得:x=2y-84
解得:x=56,y=70
∴
11.2与三角形有关的角
知识框架
一、基础知识点
知识点1
三角形内角和定理
定理:三角形三个内角和等于180度
直角三角形的两个锐角互余
例1.△ABC中,若∠A=60°,∠B=65°,求∠C。
答案:因为三角形内角和为180°
所以∠C=180-60-65=55°
例2.在△ABC中,若∠A:∠B:∠C=2:3:4,求∠C。
答案:设∠A=2x,则∠B=3x,∠C=4x
则2x+3x+4x=180,解得:x=20°
所以∠C=80°
知识点2
三角形的外角
外角:三角形的一边和另一边的延长线组成的角(一个角的外角有2个)
外交性质:
性质一:三角形的外角等于它不相邻两内角和
性质二:三角形外角和相邻内角和为180度
性质三:三角形外角和为360度
例1.如图,求x的值。
答案:根据三角形外角性质:x+80=x+x+20
解得:x=60
例2.如图,已知AB∥CD,若∠C=70°,∠F=30°,求∠A的度数。
答案:∵AB∥CD,∠C=70°
∴∠FEB=70°
∵∠FEB为△AFE的外角
∴∠A+∠F=∠FEB
∵∠F=30°
∴∠A=70-30=40°
二、典型题型
题型1
方程思想求角度
性质:(1)三角形内角和=180°;
(2)对顶角相等,邻补角互补;
(3)三角形外角=不相邻两个内角和。
解题技巧:若图形中角比较多,用设未知数方法,利用上述3条性质,将图形角度之间的关系转化为方程的形式求解。
例1.在△ABC中,∠A-∠B=30°,∠C=4∠B,求∠C的度数。
答案:设∠B=x,则∠A=x+30,∠C=4x
x+30+x+4x=180
解得:x=25
∠C=4x=100°
例2.如图,△ABC中,D是BC上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠DAC的度数。
答案:设∠1=x,则∠2=x
∵∠3时△ADB外角
∴∠3=∠1+∠2=2x
∵∠3=∠4
∴∠4=2x
在△ABC中:∠2+∠4+∠BAC=180°,即x+2x+63=180
解得:x=39°
∴∠DAC=63-39=24°
例3.如图,在△ABC中,BD平分∠ABC,∠1=∠A,∠2=∠C,求∠A的度数。
答案:设∠1=x,∠2=y
根据题意得:∠1=∠DBC=∠A=x
∠2=∠C=y
在△BDC中:x+y+y=180
在△ABC中,x+x+x+y=180
解得:x=36,y=72
∴∠A=36°
题型2
转化思想求角度
解题技巧:求解多个角度和问题时,先利用三角形角度间的基本性质,将不规则图形中的角度转化到同一个三角形(多边形)中;再利用三角形(多边形)内角和性质求解角度。
例1.如图,求∠A+∠B+∠C+∠D+∠E的度数。
答案:连接BC
∵∠EFD=∠BFC
∴∠E+∠D=∠FBC+∠FCB
∴∠A+∠ABD+∠ACE+∠D+∠F=∠A+∠ABC+∠ACB=180°
例2.如图,六边形ABCDEF中,∠A=∠D,∠B=∠E,∠C=∠F,证明AF∥CD。
证明:连接CF
∵∠A=∠D,∠B=∠E
又∵四边形ABCF和四边形CDEF内角和都为360°
∴∠BCF+∠AFC=∠DCF+∠CFE
①
∵∠BCD=∠AFE
∴∠BCF+∠FCD=∠AFC+∠CFE
②
①+②得:2∠FCD+∠CFE+∠BCF=2∠AFC+∠CFE+∠BCF
∴∠FCD=∠AFC
∴AF∥CD
例3.如图,△ABC的外角平分线BP、CP交于点P,PE⊥AC于E,PF⊥AB于F,∠A=70°,求∠FPB+∠EPC的度数。
答案:设∠CBP=x,∠BCP=y,则∠FBP=x,∠PCE=y,∠ABC=180-2x,∠ACB=180-2y
在△ABC中,∠A+(180-2x)+(180-2y)=180
①
在△BCP中,x+y+∠BPC=180
②
联立①、②可得:∠BPC=90-
在四边形AEPF中,∵∠PFB=∠PEC=90°
∴∠A+∠FPE=180°,即∠A+∠FPB+∠EPC+∠BPC=180.
将∠BPC代入,化简得:90++(∠FPB+∠EPC)=180
∵∠A=70°
∴(∠FPB+∠EPC)=180-90-35=55°
题型3
整体思想求角度
解题技巧:根据题干特点,有时单一的看待某个角度,难以解出题目要求的角度。这时,需要将2个角或多个角看成一个整体,在利用三角形内角和等性质进行转化求解。
例1.如图,点D在△ABC内,且∠BDC=120°,∠1+∠2=55°,求∠A。
答案:∵∠BDC=120°
∴∠DBC+∠DCB=60°
∵∠1+∠2=55°
∴∠ABC+∠ACB=60+55=115°
∴∠A=65°
例2.如图,将△ABC沿EF折叠,使点C落在点D处,求∠1,∠2与∠C的数量关系。
答案:∵∠1+∠DEC+∠2+∠DFC=360=∠D+∠C+∠DEC+∠DFC
∴∠1+∠2=∠D+∠C
∵△AEF是△CEF折叠得到
∴∠D=∠C
∴∠1+∠2=2∠C
题型4
数学模型—角平分线模型
性质:角平分线将一个角平分为相等的两部分
解题技巧:此类题型,往往会告知多个角平分线,要求求解某一特定角。建议设平分后的角为未知数,利用方程的思想,转化为求解方程的形式来求解特定的角。
例1.已知△ABC中,点P为∠ABC和外角∠ACD的角平分线的交点,证明∠P=
证明:设∠ABP=∠PBC=x,∠PCA=∠PCD=y,∠ACB=180-2y
在△ABC中,∠A+2x+(180-2y)=180
在△BCP中,x+y+(180-2y)+∠P=180
联立化简得:∠P=90°+
例2.如图,在四边形ABCD中,AE平分∠BAD,DE平分∠ADC。
求∠B+∠C与∠AED。
答案:设∠BAE=x=∠EAD,设∠EDA=∠EDC=y
在△AED中,∠AED+x+y=180°
在四边形ABCD中,∠B+∠C+2x+2y=360°
联立化简得:∠B+∠C=2∠AED
题型5
数学模型—对顶三角形模型
性质:若两个三角形有一个对顶角,则这两个对顶角相等,那么这两个三角形剩下的两个角的和相等。
解题技巧:利用对顶三角形另两个角的和相等的性质,列写对顶三角形另两个角之和相等的等式,通过转化,求解出题干要求的角度。
例1.如图,AC,BD相交于点O,BP,CP分别平分∠ABD,∠ACD,且交于点P。若BP、CP分别为∠ABD、∠ACD的外角平分线,求∠P与∠A、∠D的关系。
答案:设∠DCP=∠PCA=x,设∠ABP=∠PBD=y
在△PCE与△AFB中:∠P+x=∠A+y
在△DCO与△ABO中:∠D+2x=∠A+2y
联立化简得:2∠P=∠A+∠D
题型6
分类讨论思想求角度
解题技巧:当题目中未出现图形时,往往有多解情况,需要分类讨论。
(1)等腰三角形中,腰和底的讨论
锐角、直角、钝角三角形高的讨论
例1.在等腰△ABC中,∠A=80°,求∠B。
答案:情况一:设等腰三角形的腰为∠A和∠B,则∠B=80°
情况二:设等腰三角形的腰为∠A和∠C,则∠A=∠C=80°,∠B=20°
情况三:设等腰三角形的腰为∠B和∠C,则∠B=∠C=50°
例2.在等腰△ABC中,∠A=60°,求∠B。
答案:情况一:设等腰三角形的腰为∠A和∠B,则∠B=60°
情况二:设等腰三角形的腰为∠A和∠C,则∠A=∠C=60°,∠B=60°
情况三:设等腰三角形的腰为∠B和∠C,则∠B=∠C=60°(重复,舍去)
例3.已知AD为△ABC的高,∠BAD=70°,∠CAD=20°,求∠BAC的度数。
答案:如图,有2种情况
情况一
情况二
情况一:∵∠BAD=70°,∠CAD=20°
∴∠CAB=70+20=90°
情况二:∵∠BAD=70°,∠CAD=20°
∴∠CAB=70-20=50°
11.3多边形及其内角和
知识框架
一、基础知识点
知识点1
多边形的有关概念
多边形:在平面内,由一些线段首位顺次连接线段组成的图形。有n条边组成,我们就称为n边形。
内角:多边形相邻两边组成的角。n边形就有n个内角
外角:多边形的边与它的邻边的延长线组成的角
对角线:连接多边形不相邻的两个顶点组成的线段。
解释:n个顶点,每个顶点不相邻顶点有(n-3)个,重复计数一次,乘
凸多边形:画出多边形的任何一条边的直线,整个多边形都在直线同一侧。反之,则叫凹多边形。
正多边形:各个角都相等,且各条边相等的多边形。
例1.下列图形中,是正多边形是的(
)
A.直角三角形
B.等腰三角形
C.长方形
D.正方形
答案:D
正多边形:每条边相等且每个角相等的多变形为正三角形
知识点2
多边形的内角和
n边形内角和为(n-2)
180
解释:n边形可分解为(n-2)个三角形,三角形内角和为180度
例1.
四边形的内角和为:
答案:180×(4-2)=360°
例2.
一个多边形的内角和是720°,则这个多边形的边数为:
答案:180×(n-2)=720
解得:n=6
例3.凸n边形的内角和为1260°,则从一个顶点出发引的对角线条数是:
答案:180×(n-2)=1260
解得:n=9
从一个顶点引发的对角线条数是:n-3=6条
知识点3
多边形的外角和
1)定理:多边形外角和为360°
注:①多边形内角和与边n有关,等于(n-2)度
②多边形外角和与边n无关,都等于360度
例1.多边形的外角和为:
答案:外角和为360°
例2.正十边形的每个外角为:
答案:无论几边形,外角和都为360°
二、典型题型
题型1
已知多边形内角和,求边
性质:多边形内角和=180(n-2)
解题技巧:利用多边形内角和公式,设边为n,列写内角和公式方程求解边n。注意理解性记忆公式,切勿强记。
例1.如果一个多边形内角和为720°,求这个多边形的边数。
答案:180×(n-2)=720
n=6
题型2
已知多边形的边,求内角
性质:多边形内角和=180(n-2)
解题技巧:先利用多边形内角和公式,将边数n代入公式求出内角和;再结合图形特点,求出提高要求的角度。
例1.如图,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,求∠3+∠1-∠2。
答案:正三角形内角为:
正四边形内角为:
正五边形内角为:
正六边形内角为:
∴∠3=90°-60°=30°
∠2=108°-90°=18°
∠1=120°-108°=12°
∴∠3+∠1-∠2=30+12-18=24°
例2.
如图,平面上两个正方形与正五边形都有一条公共边,则∠=
答案:正四边形内角为:
正五边形内角为:
根据图形得:108+90+90+a=360
得:a=72°
题型3
已知内、外角的关系,求边数
性质:(1)多边形内角和=180(n-2)
(2)多边形外角和为360度
解题技巧:设多边形边数为n,牢牢把握多边形外角和为360度这个不变量,根据题干内、外角之间的关系,列写含有n的方程,从而求解多边形边数n。
例1.一个多边形的内角和是外角和的3倍,求这个多边形的边数。
答案:设多边形边数为n
则:180×(n-2)=3×180
解得:n=5
例2.
一个多边形中各内角相等,且每个内角与外角之差的绝对值为60°,求这个多边形的边数
答案:设多边形边数为n,则内角为:
外角为:180-
根据题意,则:=60
化简得:或
解得:n=3或n=6
三、难点题型
题型1
多边形的边和角
性质:(1)多边形内角和:180(n-2);
(2)多边形外角和:360°;
(3)多边形对角线:。
解题技巧:此类题型比较灵活,要紧抓住边这个条件。无论是内角和、对角线都仅与边有关系。因此,在解决此类问题时,要想办法先求出多边形的边,在依据题目要求进行求解。在条件比较复杂情况下,可设多边形的边为未知数,转化为方程求解。
例1.如图,一个多边形纸片按图示的剪发剪去一个内角后,得到一个内角和为2340°的新多边形,求原多边形的边数?
解:如图进行剪切,多边形增加了一个边,设剪切后的边为n条
则:180(n-2)=2340
n=15
所以原多边形的边数为:n-1=15-1=14
例2.
如图,以六边形的每个顶点为圆心,1为半径画圆,则图中阴影部分的面积为:
解:6边形内角和为:180×(6-2)=720°
阴影部分面积为6个小扇形组成,它们的圆心角和为6变形内角和,为720°
根据扇形面积公式,阴影部分面积==2π
例3.在一个多边形中,除了两个内角外,其余的内角和为2002°,求这个多边形的边数。
解:设这个多边形为n,两个内角和为x
则:180(n-2)-x=2002
化简得:180n=2362+x
∵0<x<360
∴2362<2360+x<2762
∴2362<180n<2762
解得:
因为n为整数,所以n=14或n=15
