北师大版八年级数学下册6.2平行四边形的性质和判定一课一练习题(Word版,含答案)
文档属性
| 名称 | 北师大版八年级数学下册6.2平行四边形的性质和判定一课一练习题(Word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 568.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 22:33:58 | ||
图片预览




文档简介
《平行四边形的性质和判定》习题
一、选择题
1.在中,,则的大小为(
)
A.
B.
C.
D.
2.如图,在平行四边形中,,则∠B的度数是(
)
A.30°
B.75°
C.100°
D.150°
3.已知平面直角坐标系中有O、A、B、C
四个点,其中点O
(0,0),
A(3,0),
B(1,1),若四边形OABC是平行四边形,则点C
的坐标为
(
)
A.(4,-1)
B.(4,1)
C.(2,-1)
D.(-2,1)
4.中,的度数比可能是(
)
A.
B.
C.
D.
5.平行四边形一边长是10cm,那么它的两条对角线的长度可以是( )
A.8cm和6cm
B.8cm和8cm
C.8cm和12cm
D.8cm和16cm
6.如图,的对角线交点是直角坐标系的原点,轴,若顶点坐标是,,则顶点的坐标是(
)
A.
B.
C.
D.
7.在四边形中,对角线,相交于点.给出下列四组条件:①,;②,;③,;④,.其中一定能判定这个四边形是平行四边形的条件有(
)
A.①②③
B.②③④
C.①②④
D.①③④
8.平行四边形中,对角线和相交于点,若,,,那么的取值范围是(
)
A.
B.
C.
D.
9.如图,平行四边形中,点在边上,以为折痕,将向上翻折,点正好落在上的点处,若的周长为6,的周长为14,则的长为(
)
A.4
B.6
C.8
D.10
10.如图,直线m经过点B且平行于AC,点P为直线m上的一动点,连接PC,PA,随着点P在直线m上移动,则下列说法中一定正确的是(
)
A.与全等
B.与的周长相等
C.与的面积相等
D.四边形ACBP是平行四边形
11.证明:平行四边形的对角线互相平分
已知:如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O
求证:OA=OC,OB=OD
证明:∵四边形ABCD是平行四边形,
∴…
∴∠ABO=∠CDO,∠BAO=∠DCO,
∴△AOB≌△COD,
∴OA=OC,OB=OD
其中,在“四边形ABCD是平行四边形”与“∠ABO=∠CDO,∠BAO=∠DCO”之间应补充的步骤是( )
A.AB=CD,AD=BC
B.AD//BC,AD=BC
C.AB//CD,AD//BC
D.AB//CD,AB=CD
12.如图,等腰中,点是底边上的动点(不与点,重合),过点分别作、的平行线、,交、于点、,则下列数量关系一定正确的是(
)
A.
B.
C.
D.
13.如图,为平行四边形的对角线,,于点,于点,、相交于点,直线交线段的延长线于点,下列结论:①,②,③,④,⑤.正确的结论有(
)个
A.1
B.2
C.3
D.4
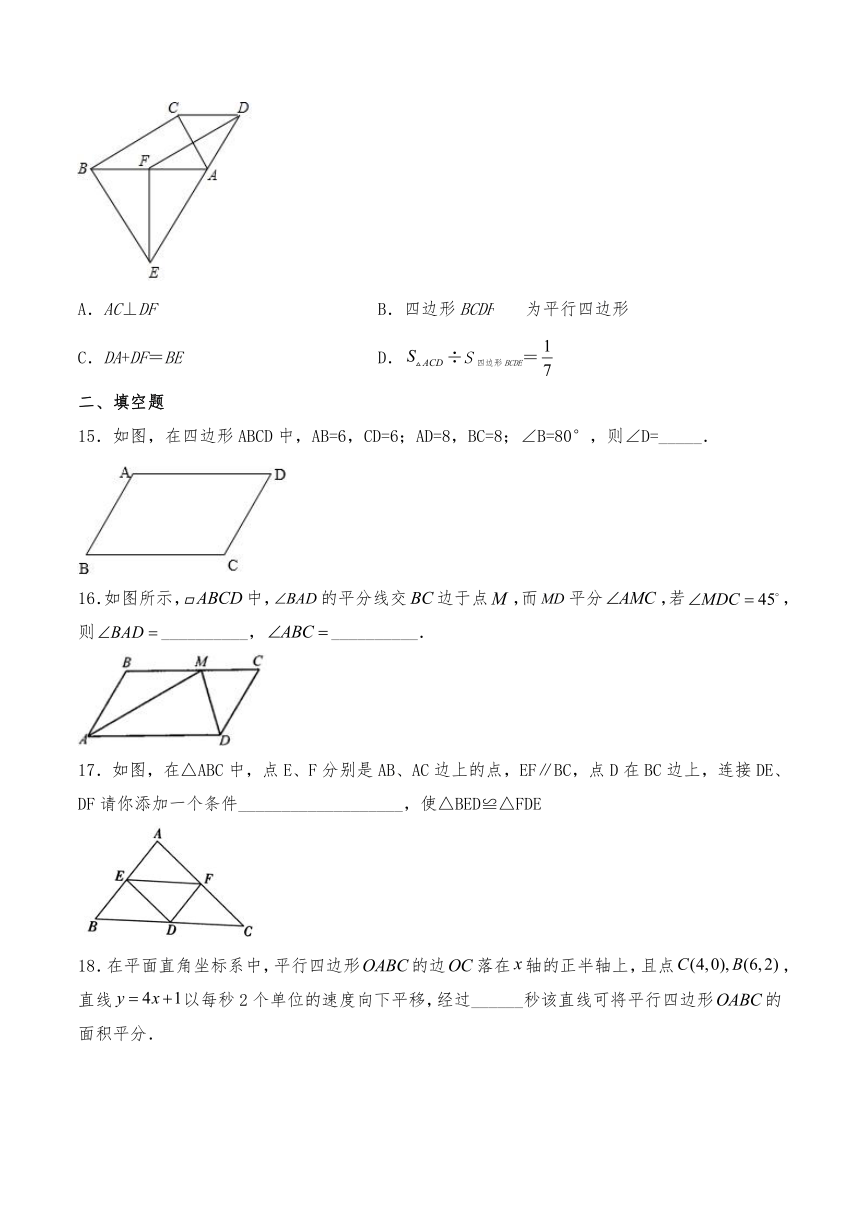
14.如图,分别以RtABC的直角边AC,斜边AB为边向外作等边三角形ACD和ABE,F为AB的中点,连接DF,EF,∠ACB=90°,∠ABC=30°,其中错误的是(
)
A.AC⊥DF
B.四边形BCDF为平行四边形
C.DA+DF=BE
D.÷S四边形BCDE=
二、填空题
15.如图,在四边形ABCD中,AB=6,CD=6;AD=8,BC=8;∠B=80°,则∠D=_____.
16.如图所示,中,的平分线交边于点,而平分,若,则__________,__________.
17.如图,在△ABC中,点E、F分别是AB、AC边上的点,EF∥BC,点D在BC边上,连接DE、DF请你添加一个条件___________________,使△BED≌△FDE
18.在平面直角坐标系中,平行四边形的边落在轴的正半轴上,且点,直线以每秒2个单位的速度向下平移,经过______秒该直线可将平行四边形的面积平分.
三、解答题
19.如图,将正方形网格放置在平面直角坐标系中,其中每个小正方形的边长均为1,点A、B、C的坐标分别为A(1,3)、B(4,4)、C(2,1).
(1)画出△ABC关于原点成中心对称的图形△A1B1C1,则点A的对应点A1的坐标为
;
(2)若在坐标轴上有一点D,使点A、B、C、D构成平行四边形,直接写出点D的坐标.
20.在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的四边形为整点四边形.如图,已知整点A(1,2),B(5,2),请在所给网格区域(不含边界)上按要求画整点四边形.
(1)在图1中画一个以A,B,C,D为顶点的平行四边形,使AO=CO.
(2)在图2中画一个以A,B,C,D为顶点的平行四边形,使点C的横坐标与纵坐标的和等于点A的纵坐标的3倍.
21.操作探究:
(1)现有一块等腰三角形纸板,为底边,量得周长为,底比一腰多.若把这个三角形纸板沿其对称轴剪开,拼成一个四边形,请在下列方框中画出你能拼成的各种四边形的示意图,并在图中标出四边形的各边长;
(2)计算拼成的各个四边形的两条对角线长的平方和.
22.如图,在平行四边形中,点E是CD边的中点,连接AE并延长交BC的延长线于点F,连接BE,.
(1)求证:AE平分;
(2)若,,求平行四边形的面积.
23.如图,在平行四边形ABCD中,AD=6,点E在边AD上,且AE=2
(1)若直线l经过点E,将该平行四边形的面积平分,并与平行四边形的另一边交于点F,用无刻度的直尺画出点F;
(2)连接AF,CE,判断四边形AFCE的形状,并说明理由.
24.如图所示,在中,对角线,相交于点O,,E,F为直线上的两个动点(点E,F始终在的外面),且,连结,,,.
(1)求证:四边形为平行四边形.
(2)若,上述结论还成立吗?若呢?
(3)若平分,,求四边形的周长.
25.如图,直线分别与轴、轴交于、两点,与直线交于点,且.
(1)求直线的解析式;
(2)若与轴交于点,求的面积;
(3)在线段上是否存在一点,过点作轴交于点,使得四边形是平行四边形?若存在,求出点的坐标;若不存在,请说明理由.
26.如图,在四边形中,.动点P从点B出发,沿射线的方向以每秒的速度运动到C点返回,动点Q从点A出发,在线段上以每秒的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动时间为t(秒).
(1)当时,若四边形是平行四边形,求出满足要求的t的值;
(2)当时,若以C,D,Q,P为顶点的四边形面积为,求相应的t的值;
(3)当时,若以C,D,Q,P为顶点的四边形面积为,求相应的t的值.
答案
一、选择题
1.B.2.A.3.D.4.B.5.D.6.A.7.A.8.D.
9.A.10.C.11.D.12.A.13.C.14.C.
二、填空题
15.80°
16.60°
120°.
17.BD=FE.
18.6.
三、解答题
19.
解:(1)作A、B、C关于点O的对称点A1、B1、C1,顺次连结A1B1、B1C1、C1A1,
则△A1B1C1与△ABC关于原点O成中心对称,
关于原点对称坐标特征是横纵坐标符号改变,
∵A(1,3),
∴A1(-1,-3),
故答案为A1(-1,-3);
(2)∵A、B、C、D构成平行四边形,
∴AB=DC,
设点D坐标为(m,0),
∴有4-1=2-m,
∴m=-1,
∴D(-1,0).
20.
(1)如图,四边形ACBD或四边形ABD′C即为所求作.
(2)如图,四边形ACBD或四边形ABC′D′即为所求作.
21.
解:(1)如图所示:
(2)设AB=AC=xcm,则BC=(x+2)cm,
由题意得(x+2)+2x=32,解得x=10cm.
因此AB=AC=10cm,则BC=12cm,
过点A作AD⊥BC于D,
∴BD=CD=6cm,
∴AD=8cm.
可以拼成四种四边形,如上图所示.
如图1,两对角线长的平方和为102+102=200;
如图2,AC2=,
∴两对角线长的平方和为;
如图3,BC2=,
∴两对角线长的平方和为;
如图4,∵×AB×CO=×AC×BC,
10CO=6×8.
∴CO=4.8cm,CD=9.6cm.
∴两对角线长的平方和为.
22.
解:(1)在中,
∴
又∵且
∴
∴,
又且
∴
∴
∴平分;
(2)∵
∴
∴,
∵
∴
∴
23.
解:(1)如图所示,点F即为所求作的点.
(2)四边形AFCE是平行四边形,理由是:
∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC.
∴∠OAE=∠OCF.
∵∠AOE=∠COF,
∴△AOE≌△COF.
∴OE=OF.
∴四边形AFCE是平行四边形.
24.
解:(1)证明:四边形是平行四边形,
,.
,,
,
,
四边形为平行四边形.
(2),,
,
,
四边形为平行四边形.
上述结论成立,
由此可得出结论:若,,则四边形为平行四边形.
(3)在中,,
.
平分,
,
,
.
,
,
是的垂直平分线,
.
,
是等边三角形,
,
.
25.
解:(1)∵OA=8,
∴A(8,0),
将A(8,0)
代入,
得,解得,
故;
(2)由与轴交于点,
∴,
由与轴交于,
∴,
∴,
联立,解得,
∴,
∴;
(3)存在,
根据题意,若四边形是平行四边形,
则,
设,则,
则,
解得,,
∴.
26.
解:(1)∵四边形PQDC是平行四边形,
∴DQ=CP,
当0<t<10.5时,P、Q分别沿AD、BC运动,如图1所示:
∵DQ=AD-AQ=16-t,
CP=21-2t
∴16-t=21-2t
解得:t=5;
即当t=5秒时,四边形PQDC是平行四边形;
(2)当0<t<10.5时,P、Q分别沿AD、BC运动,如图1所示:
CP=21-2t,DQ=16-t,
若以C,D,Q,P为顶点的四边形面积为60cm2,
则(DQ+CP)×AB=60,
即(16-t+21-2t)×12=60,
解得:t=9;
即当0<t<10.5时,若以C,D,Q,P为顶点的四边形面积为60cm2,t的值为9秒;
(3)当10.5≤t<16时,如图2所示,点P到达C点返回,CP=2t-21,DQ=16-t,
则同(2)得:(DQ+CP)×AB=60,
即(16-t+2t-21)×12=60,
解得:t=15.
即当10.5≤t<16时,若以C,D,Q,P为顶点的四边形面积为60cm2,t的值为15秒.
一、选择题
1.在中,,则的大小为(
)
A.
B.
C.
D.
2.如图,在平行四边形中,,则∠B的度数是(
)
A.30°
B.75°
C.100°
D.150°
3.已知平面直角坐标系中有O、A、B、C
四个点,其中点O
(0,0),
A(3,0),
B(1,1),若四边形OABC是平行四边形,则点C
的坐标为
(
)
A.(4,-1)
B.(4,1)
C.(2,-1)
D.(-2,1)
4.中,的度数比可能是(
)
A.
B.
C.
D.
5.平行四边形一边长是10cm,那么它的两条对角线的长度可以是( )
A.8cm和6cm
B.8cm和8cm
C.8cm和12cm
D.8cm和16cm
6.如图,的对角线交点是直角坐标系的原点,轴,若顶点坐标是,,则顶点的坐标是(
)
A.
B.
C.
D.
7.在四边形中,对角线,相交于点.给出下列四组条件:①,;②,;③,;④,.其中一定能判定这个四边形是平行四边形的条件有(
)
A.①②③
B.②③④
C.①②④
D.①③④
8.平行四边形中,对角线和相交于点,若,,,那么的取值范围是(
)
A.
B.
C.
D.
9.如图,平行四边形中,点在边上,以为折痕,将向上翻折,点正好落在上的点处,若的周长为6,的周长为14,则的长为(
)
A.4
B.6
C.8
D.10
10.如图,直线m经过点B且平行于AC,点P为直线m上的一动点,连接PC,PA,随着点P在直线m上移动,则下列说法中一定正确的是(
)
A.与全等
B.与的周长相等
C.与的面积相等
D.四边形ACBP是平行四边形
11.证明:平行四边形的对角线互相平分
已知:如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O
求证:OA=OC,OB=OD
证明:∵四边形ABCD是平行四边形,
∴…
∴∠ABO=∠CDO,∠BAO=∠DCO,
∴△AOB≌△COD,
∴OA=OC,OB=OD
其中,在“四边形ABCD是平行四边形”与“∠ABO=∠CDO,∠BAO=∠DCO”之间应补充的步骤是( )
A.AB=CD,AD=BC
B.AD//BC,AD=BC
C.AB//CD,AD//BC
D.AB//CD,AB=CD
12.如图,等腰中,点是底边上的动点(不与点,重合),过点分别作、的平行线、,交、于点、,则下列数量关系一定正确的是(
)
A.
B.
C.
D.
13.如图,为平行四边形的对角线,,于点,于点,、相交于点,直线交线段的延长线于点,下列结论:①,②,③,④,⑤.正确的结论有(
)个
A.1
B.2
C.3
D.4
14.如图,分别以RtABC的直角边AC,斜边AB为边向外作等边三角形ACD和ABE,F为AB的中点,连接DF,EF,∠ACB=90°,∠ABC=30°,其中错误的是(
)
A.AC⊥DF
B.四边形BCDF为平行四边形
C.DA+DF=BE
D.÷S四边形BCDE=
二、填空题
15.如图,在四边形ABCD中,AB=6,CD=6;AD=8,BC=8;∠B=80°,则∠D=_____.
16.如图所示,中,的平分线交边于点,而平分,若,则__________,__________.
17.如图,在△ABC中,点E、F分别是AB、AC边上的点,EF∥BC,点D在BC边上,连接DE、DF请你添加一个条件___________________,使△BED≌△FDE
18.在平面直角坐标系中,平行四边形的边落在轴的正半轴上,且点,直线以每秒2个单位的速度向下平移,经过______秒该直线可将平行四边形的面积平分.
三、解答题
19.如图,将正方形网格放置在平面直角坐标系中,其中每个小正方形的边长均为1,点A、B、C的坐标分别为A(1,3)、B(4,4)、C(2,1).
(1)画出△ABC关于原点成中心对称的图形△A1B1C1,则点A的对应点A1的坐标为
;
(2)若在坐标轴上有一点D,使点A、B、C、D构成平行四边形,直接写出点D的坐标.
20.在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的四边形为整点四边形.如图,已知整点A(1,2),B(5,2),请在所给网格区域(不含边界)上按要求画整点四边形.
(1)在图1中画一个以A,B,C,D为顶点的平行四边形,使AO=CO.
(2)在图2中画一个以A,B,C,D为顶点的平行四边形,使点C的横坐标与纵坐标的和等于点A的纵坐标的3倍.
21.操作探究:
(1)现有一块等腰三角形纸板,为底边,量得周长为,底比一腰多.若把这个三角形纸板沿其对称轴剪开,拼成一个四边形,请在下列方框中画出你能拼成的各种四边形的示意图,并在图中标出四边形的各边长;
(2)计算拼成的各个四边形的两条对角线长的平方和.
22.如图,在平行四边形中,点E是CD边的中点,连接AE并延长交BC的延长线于点F,连接BE,.
(1)求证:AE平分;
(2)若,,求平行四边形的面积.
23.如图,在平行四边形ABCD中,AD=6,点E在边AD上,且AE=2
(1)若直线l经过点E,将该平行四边形的面积平分,并与平行四边形的另一边交于点F,用无刻度的直尺画出点F;
(2)连接AF,CE,判断四边形AFCE的形状,并说明理由.
24.如图所示,在中,对角线,相交于点O,,E,F为直线上的两个动点(点E,F始终在的外面),且,连结,,,.
(1)求证:四边形为平行四边形.
(2)若,上述结论还成立吗?若呢?
(3)若平分,,求四边形的周长.
25.如图,直线分别与轴、轴交于、两点,与直线交于点,且.
(1)求直线的解析式;
(2)若与轴交于点,求的面积;
(3)在线段上是否存在一点,过点作轴交于点,使得四边形是平行四边形?若存在,求出点的坐标;若不存在,请说明理由.
26.如图,在四边形中,.动点P从点B出发,沿射线的方向以每秒的速度运动到C点返回,动点Q从点A出发,在线段上以每秒的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动时间为t(秒).
(1)当时,若四边形是平行四边形,求出满足要求的t的值;
(2)当时,若以C,D,Q,P为顶点的四边形面积为,求相应的t的值;
(3)当时,若以C,D,Q,P为顶点的四边形面积为,求相应的t的值.
答案
一、选择题
1.B.2.A.3.D.4.B.5.D.6.A.7.A.8.D.
9.A.10.C.11.D.12.A.13.C.14.C.
二、填空题
15.80°
16.60°
120°.
17.BD=FE.
18.6.
三、解答题
19.
解:(1)作A、B、C关于点O的对称点A1、B1、C1,顺次连结A1B1、B1C1、C1A1,
则△A1B1C1与△ABC关于原点O成中心对称,
关于原点对称坐标特征是横纵坐标符号改变,
∵A(1,3),
∴A1(-1,-3),
故答案为A1(-1,-3);
(2)∵A、B、C、D构成平行四边形,
∴AB=DC,
设点D坐标为(m,0),
∴有4-1=2-m,
∴m=-1,
∴D(-1,0).
20.
(1)如图,四边形ACBD或四边形ABD′C即为所求作.
(2)如图,四边形ACBD或四边形ABC′D′即为所求作.
21.
解:(1)如图所示:
(2)设AB=AC=xcm,则BC=(x+2)cm,
由题意得(x+2)+2x=32,解得x=10cm.
因此AB=AC=10cm,则BC=12cm,
过点A作AD⊥BC于D,
∴BD=CD=6cm,
∴AD=8cm.
可以拼成四种四边形,如上图所示.
如图1,两对角线长的平方和为102+102=200;
如图2,AC2=,
∴两对角线长的平方和为;
如图3,BC2=,
∴两对角线长的平方和为;
如图4,∵×AB×CO=×AC×BC,
10CO=6×8.
∴CO=4.8cm,CD=9.6cm.
∴两对角线长的平方和为.
22.
解:(1)在中,
∴
又∵且
∴
∴,
又且
∴
∴
∴平分;
(2)∵
∴
∴,
∵
∴
∴
23.
解:(1)如图所示,点F即为所求作的点.
(2)四边形AFCE是平行四边形,理由是:
∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC.
∴∠OAE=∠OCF.
∵∠AOE=∠COF,
∴△AOE≌△COF.
∴OE=OF.
∴四边形AFCE是平行四边形.
24.
解:(1)证明:四边形是平行四边形,
,.
,,
,
,
四边形为平行四边形.
(2),,
,
,
四边形为平行四边形.
上述结论成立,
由此可得出结论:若,,则四边形为平行四边形.
(3)在中,,
.
平分,
,
,
.
,
,
是的垂直平分线,
.
,
是等边三角形,
,
.
25.
解:(1)∵OA=8,
∴A(8,0),
将A(8,0)
代入,
得,解得,
故;
(2)由与轴交于点,
∴,
由与轴交于,
∴,
∴,
联立,解得,
∴,
∴;
(3)存在,
根据题意,若四边形是平行四边形,
则,
设,则,
则,
解得,,
∴.
26.
解:(1)∵四边形PQDC是平行四边形,
∴DQ=CP,
当0<t<10.5时,P、Q分别沿AD、BC运动,如图1所示:
∵DQ=AD-AQ=16-t,
CP=21-2t
∴16-t=21-2t
解得:t=5;
即当t=5秒时,四边形PQDC是平行四边形;
(2)当0<t<10.5时,P、Q分别沿AD、BC运动,如图1所示:
CP=21-2t,DQ=16-t,
若以C,D,Q,P为顶点的四边形面积为60cm2,
则(DQ+CP)×AB=60,
即(16-t+21-2t)×12=60,
解得:t=9;
即当0<t<10.5时,若以C,D,Q,P为顶点的四边形面积为60cm2,t的值为9秒;
(3)当10.5≤t<16时,如图2所示,点P到达C点返回,CP=2t-21,DQ=16-t,
则同(2)得:(DQ+CP)×AB=60,
即(16-t+2t-21)×12=60,
解得:t=15.
即当10.5≤t<16时,若以C,D,Q,P为顶点的四边形面积为60cm2,t的值为15秒.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
