北师大版八年级数学下册6.3-6.4三角形的中位线与多边形角度计算一课一练习题1(Word版,含答案)
文档属性
| 名称 | 北师大版八年级数学下册6.3-6.4三角形的中位线与多边形角度计算一课一练习题1(Word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 451.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 00:00:00 | ||
图片预览




文档简介
《三角形的中位线与多边形角度计算》习题1
一、选择题
1.如图,点D和点E分别是BC和BA的中点,已知AC=4,则DE为( )
A.1
B.2
C.4
D.8
2.如图,AB∥CD,E,F分别为AC,BD的中点,若AB=5,CD=3,则EF的长为( )
A.2.5
B.2
C.1.5
D.1
3.如图,平行四边形ABCD的周长为36,对角线AC、BD相交于点O,
点E是CD的中点,BD=12,则△DOE的周长为(
)
A.12
B.15
C.18
D.21
4.六边形的外角和为(
)
A.180°
B.360°
C.720°
D.1080°
5.下列哪个度数不可能是一个多边形的内角和(
)
A.
B.
C.
D.
6.如图所示,一个等边三角形纸片剪去一个角后变成一个四边形,则图中的度数为(
)
A.
B.
C.
D.
7.一个多边形的内角和为720度,那么这个多边形一共有(
)条对角线.
A.9
B.15
C.6
D.18
8.如图,等于(
)
A.360°
B.335°
C.385°
D.405°
9.一个五边形截去个角后剩下的多边形内角和是(
)
A.
B.
C.
D.或或
10.如图,中,,,对角线、相交于点,点、、、分别是、、、的中点,则下列说法正确的是(
)
A.
B.的面积是的面积的2倍
C.
D.四边形是平行四边形
11.一个多边形的每个内角都是150°,这个多边形是(
)
A.八边形
B.十边形
C.十二边形
D.十四边形
12.如图,△ABC中,∠B=90°,过点C作AB的平行线,与∠BAC的平分线交于点D,若AB=6,BC=8.E,F分别是BC,AD的中点,则EF的长为
(
)
A.1
B.1.5
C.2
D.4
13.如图,在RtABC中,∠C=90°,AC=6,BC=9,点D为BC边上的中点,将ACD沿AD对折,使点C落在同一平面内的点处,连接,则的长为(
)
A.
B.
C.
D.
14.如图,在中,,,、分别是其角平分线和中线,过点作于,交于,连接,则线段的长为(
)
A.1
B.2
C.
D.7
二、填空题
15.一个三角形的周长是12cm,则这个三角形各边中点围成的三角形的周长为___.
16.若正n边形的一个外角是一个内角的时,则_________.
17.如图,ABC中,DE垂直平分BC,CE平分∠ACB,FG为ACE的中位线,连接DF,若∠DFG=108°,则∠AED=_____.
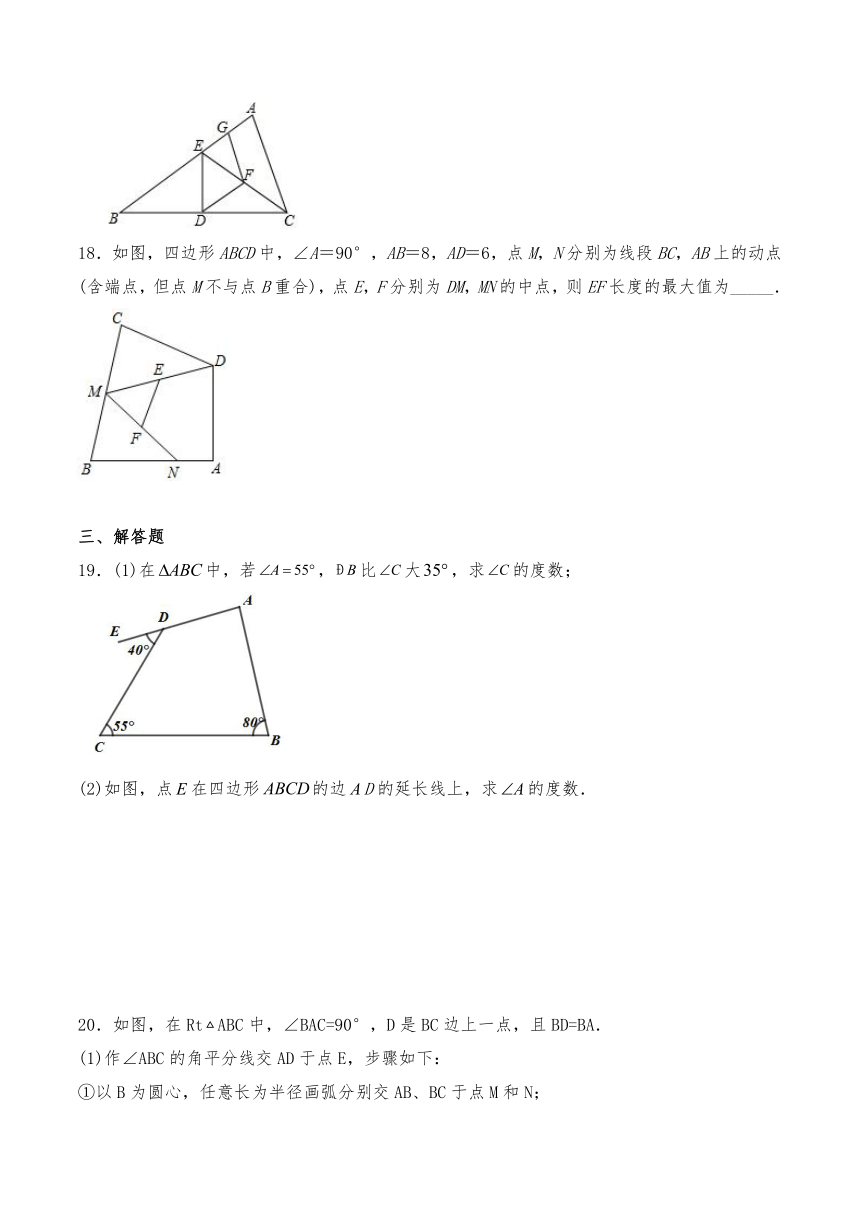
18.如图,四边形ABCD中,∠A=90°,AB=8,AD=6,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为_____.
三、解答题
19.(1)在中,若,比大,求的度数;
(2)如图,点在四边形的边D的延长线上,求的度数.
20.如图,在RtABC中,∠BAC=90°,D是BC边上一点,且BD=BA.
(1)作∠ABC的角平分线交AD于点E,步骤如下:
①以B为圆心,任意长为半径画弧分别交AB、BC于点M和N;
②分别以M、N为圆心,大于的长为半径画弧,两弧交于点P;
③连结BP并延长交AD于点E.则BE是∠ABC的角平分线,所以AE
DE填“=”、“<”、“>”)
(2)作CD的中点F,连接EF,若∠EBD=20°,求∠BEF的度数.
21.如图,在中,为中点,过点作交于点,且,连接,,.
(1)求证:四边形为平行四边形;
(2)若,,,求的长.
22.如图,在五边形ABCDE中,AP平分,BP平分.
(1)五边形ABCDE的内角和为
度;
(2)若,,,求的度数.
23.如图,将六边形纸片ABCDEF沿虚线剪去一个角(∠BCD)后,得到∠1+∠2+∠3+∠4+∠5=460°.
(1)求六边形ABCDEF的内角和;
(2)求∠BGD的度数.
24.已知:如图,在中,中线交于点分别是的中点.
求证:(1);
(2)和互相平分.
25.如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是________,位置关系是________;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
26.(1)如图1,在△ABC中,已知OB,OC分别平分∠ABC,∠ACB,BP,CP分别平分∠ABC,∠ACB,的外角∠DBC,∠ECB.
?①若∠A=50?,则∠O=______,∠P=______;
?②若∠A=α,则∠O=______,∠P=______.(用含α的式子表示)
(2)如图2,在四边形ABCD中,BP,CP分别平分外角∠EBC,∠FCB,请探究∠P与∠A,∠D的数量关系,并说明理由;
(3)如图3,在六边形ABCDEF中,CP,DP分别平分外角∠GCD,∠HDC,请直接写出∠P与∠A,∠B,∠E,∠F的数量关系______.
答案
一、选择题
1.B.2.D.3.B.4.B.5.B.6.C.7.A.8.C.
9.D.10.D.11.C.12.C.13.B.14.A
二、填空题
15.6
cm.
16.5
17.126°
18.5
三、解答题
19.解:∵
,,,
∴
,
解得.
∵
,
∴
.
∵
,
∴
.
20.
解:
(1)∵BD=BA,BE平分∠ABC,
∴AE=DE,
故答案为:=;
(2)∵BE是∠ABC的角平分线,AB=BD,
∴∠DBE=∠ABE=20°,BE⊥AD,
∴∠BEA=90°,
∴∠ABE+∠BAE=90°,
又∵∠BAC=90°,
∴∠CAE+∠BAE=90°,
∴∠ABE=∠DAC,
又∵点F为CD的中点,E为AD中点,
∴EF//AC,
∴∠DEF=∠DAC=20°,
∴∠BEF=∠BED+∠DEF=90°+20°=110°.
21.解:(1)证明:为中点,
,
,
∴点E为AC的中点,
,
,
四边形为平行四边形;
(2),,
,
过作于,
,
,
,
,
.
22.
解:(1)五边形ABCDE的内角和为,
(2)∵在五边形ABCDE中,,
,,
∴,
∵AP平分,BP平分,
∴,,
∴,
∴.
23.
解:(1)六边形ABCDEF的内角和为:180°×(6-2)=720°;
(2)∵∠1+∠2+∠3+∠4+∠5=460°,
∴∠GBC+∠C+∠CDG=720°-460°=260°,
∴∠G=360°-(∠GBC+∠C+∠CDG)=100°.
24.
(1)在△ABC中,
∵BE、CD为中线
∴AD=BD,AE=CE,
∴DE∥BC且DE=BC.
在△OBC中,
∵OF=FB,OG=GC,
∴FG∥BC且FG=BC.
∴DE∥FG
(2)由(1)知:
DE∥FG,DE=FG.
∴四边形DFGE为平行四边形.
∴和互相平分
25.
解:(1)∵点P,N是BC,CD的中点,
∴PN∥BD,PN=BD,
∵点P,M是CD,DE的中点,
∴PM∥CE,PM=CE,
∵AB=AC,AD=AE,
∴BD=CE,
∴PM=PN,
∵PN∥BD,
∴∠DPN=∠ADC,
∵PM∥CE,
∴∠DPM=∠DCA,
∵∠BAC=90°,
∴∠ADC+∠ACD=90°,
∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°,
∴PM⊥PN,
故答案为:PM=PN,PM⊥PN;
是等腰直角三角形,理由如下:
由旋转知,,
,
≌,
,
利用三角形的中位线得,,
,
是等腰三角形,
同的方法得,,
,
同的方法得,,
,
,
,
,
,
,
是等腰直角三角形.
26.
解:(1)①连结AO并延长到Q,连结PA
∵OB,OC分别平分∠ABC,∠ACB,
∴∠ABO=;∠ACO=,
∴∠BOQ=∠ABO+∠BAO,∠QOC=∠OCA+∠OAC,
∴∠BOC=∠BOQ+∠QOC=∠ABO+∠BAO+∠OCA+∠OAC,
∴∠BOC=∠BAC++,
=∠A++,
=∠A+180°-
,
=90°+,
=115°,
BP,CP分别平分∠ABC,∠ACB的外角∠DBC,∠ECB,
∴∠DBP=;∠ECP=,
∠DBP=∠BAP+∠BPA,∠ECP=∠CAP+∠CPA,
∴∠DBP+∠ECP=∠BAP+∠BPA+∠CAP+∠CPA=∠A+∠P,
∴,
∴,
∴90?+,
∴,
故答案为:115?;65?;
②由①得∠O=90°+,
,
∵∠A=α,
∴∠O=90°+,,
故答案为:∠O=90°+,,
解:,
理由如下:
在四边形ABCD中,BP,CP分别平分外角∠EBC,∠FCB,
∴∠CBP=;∠BCP=,
,
,
,
,
;
(3)延长CB,DE交直线AF与M、N如图,
由(2)得,
∴∠M=∠FAB+∠CBA-180?,∠N=∠EFA+∠DEF-180?,
∴∠M+∠N=∠FAB+∠CBA-180?+∠EFA+∠DEF-180?=∠FAB+∠CBA+∠EFA+∠DEF-360?,
∴,
∴,
∴,
故答案为:.
一、选择题
1.如图,点D和点E分别是BC和BA的中点,已知AC=4,则DE为( )
A.1
B.2
C.4
D.8
2.如图,AB∥CD,E,F分别为AC,BD的中点,若AB=5,CD=3,则EF的长为( )
A.2.5
B.2
C.1.5
D.1
3.如图,平行四边形ABCD的周长为36,对角线AC、BD相交于点O,
点E是CD的中点,BD=12,则△DOE的周长为(
)
A.12
B.15
C.18
D.21
4.六边形的外角和为(
)
A.180°
B.360°
C.720°
D.1080°
5.下列哪个度数不可能是一个多边形的内角和(
)
A.
B.
C.
D.
6.如图所示,一个等边三角形纸片剪去一个角后变成一个四边形,则图中的度数为(
)
A.
B.
C.
D.
7.一个多边形的内角和为720度,那么这个多边形一共有(
)条对角线.
A.9
B.15
C.6
D.18
8.如图,等于(
)
A.360°
B.335°
C.385°
D.405°
9.一个五边形截去个角后剩下的多边形内角和是(
)
A.
B.
C.
D.或或
10.如图,中,,,对角线、相交于点,点、、、分别是、、、的中点,则下列说法正确的是(
)
A.
B.的面积是的面积的2倍
C.
D.四边形是平行四边形
11.一个多边形的每个内角都是150°,这个多边形是(
)
A.八边形
B.十边形
C.十二边形
D.十四边形
12.如图,△ABC中,∠B=90°,过点C作AB的平行线,与∠BAC的平分线交于点D,若AB=6,BC=8.E,F分别是BC,AD的中点,则EF的长为
(
)
A.1
B.1.5
C.2
D.4
13.如图,在RtABC中,∠C=90°,AC=6,BC=9,点D为BC边上的中点,将ACD沿AD对折,使点C落在同一平面内的点处,连接,则的长为(
)
A.
B.
C.
D.
14.如图,在中,,,、分别是其角平分线和中线,过点作于,交于,连接,则线段的长为(
)
A.1
B.2
C.
D.7
二、填空题
15.一个三角形的周长是12cm,则这个三角形各边中点围成的三角形的周长为___.
16.若正n边形的一个外角是一个内角的时,则_________.
17.如图,ABC中,DE垂直平分BC,CE平分∠ACB,FG为ACE的中位线,连接DF,若∠DFG=108°,则∠AED=_____.
18.如图,四边形ABCD中,∠A=90°,AB=8,AD=6,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为_____.
三、解答题
19.(1)在中,若,比大,求的度数;
(2)如图,点在四边形的边D的延长线上,求的度数.
20.如图,在RtABC中,∠BAC=90°,D是BC边上一点,且BD=BA.
(1)作∠ABC的角平分线交AD于点E,步骤如下:
①以B为圆心,任意长为半径画弧分别交AB、BC于点M和N;
②分别以M、N为圆心,大于的长为半径画弧,两弧交于点P;
③连结BP并延长交AD于点E.则BE是∠ABC的角平分线,所以AE
DE填“=”、“<”、“>”)
(2)作CD的中点F,连接EF,若∠EBD=20°,求∠BEF的度数.
21.如图,在中,为中点,过点作交于点,且,连接,,.
(1)求证:四边形为平行四边形;
(2)若,,,求的长.
22.如图,在五边形ABCDE中,AP平分,BP平分.
(1)五边形ABCDE的内角和为
度;
(2)若,,,求的度数.
23.如图,将六边形纸片ABCDEF沿虚线剪去一个角(∠BCD)后,得到∠1+∠2+∠3+∠4+∠5=460°.
(1)求六边形ABCDEF的内角和;
(2)求∠BGD的度数.
24.已知:如图,在中,中线交于点分别是的中点.
求证:(1);
(2)和互相平分.
25.如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是________,位置关系是________;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
26.(1)如图1,在△ABC中,已知OB,OC分别平分∠ABC,∠ACB,BP,CP分别平分∠ABC,∠ACB,的外角∠DBC,∠ECB.
?①若∠A=50?,则∠O=______,∠P=______;
?②若∠A=α,则∠O=______,∠P=______.(用含α的式子表示)
(2)如图2,在四边形ABCD中,BP,CP分别平分外角∠EBC,∠FCB,请探究∠P与∠A,∠D的数量关系,并说明理由;
(3)如图3,在六边形ABCDEF中,CP,DP分别平分外角∠GCD,∠HDC,请直接写出∠P与∠A,∠B,∠E,∠F的数量关系______.
答案
一、选择题
1.B.2.D.3.B.4.B.5.B.6.C.7.A.8.C.
9.D.10.D.11.C.12.C.13.B.14.A
二、填空题
15.6
cm.
16.5
17.126°
18.5
三、解答题
19.解:∵
,,,
∴
,
解得.
∵
,
∴
.
∵
,
∴
.
20.
解:
(1)∵BD=BA,BE平分∠ABC,
∴AE=DE,
故答案为:=;
(2)∵BE是∠ABC的角平分线,AB=BD,
∴∠DBE=∠ABE=20°,BE⊥AD,
∴∠BEA=90°,
∴∠ABE+∠BAE=90°,
又∵∠BAC=90°,
∴∠CAE+∠BAE=90°,
∴∠ABE=∠DAC,
又∵点F为CD的中点,E为AD中点,
∴EF//AC,
∴∠DEF=∠DAC=20°,
∴∠BEF=∠BED+∠DEF=90°+20°=110°.
21.解:(1)证明:为中点,
,
,
∴点E为AC的中点,
,
,
四边形为平行四边形;
(2),,
,
过作于,
,
,
,
,
.
22.
解:(1)五边形ABCDE的内角和为,
(2)∵在五边形ABCDE中,,
,,
∴,
∵AP平分,BP平分,
∴,,
∴,
∴.
23.
解:(1)六边形ABCDEF的内角和为:180°×(6-2)=720°;
(2)∵∠1+∠2+∠3+∠4+∠5=460°,
∴∠GBC+∠C+∠CDG=720°-460°=260°,
∴∠G=360°-(∠GBC+∠C+∠CDG)=100°.
24.
(1)在△ABC中,
∵BE、CD为中线
∴AD=BD,AE=CE,
∴DE∥BC且DE=BC.
在△OBC中,
∵OF=FB,OG=GC,
∴FG∥BC且FG=BC.
∴DE∥FG
(2)由(1)知:
DE∥FG,DE=FG.
∴四边形DFGE为平行四边形.
∴和互相平分
25.
解:(1)∵点P,N是BC,CD的中点,
∴PN∥BD,PN=BD,
∵点P,M是CD,DE的中点,
∴PM∥CE,PM=CE,
∵AB=AC,AD=AE,
∴BD=CE,
∴PM=PN,
∵PN∥BD,
∴∠DPN=∠ADC,
∵PM∥CE,
∴∠DPM=∠DCA,
∵∠BAC=90°,
∴∠ADC+∠ACD=90°,
∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°,
∴PM⊥PN,
故答案为:PM=PN,PM⊥PN;
是等腰直角三角形,理由如下:
由旋转知,,
,
≌,
,
利用三角形的中位线得,,
,
是等腰三角形,
同的方法得,,
,
同的方法得,,
,
,
,
,
,
,
是等腰直角三角形.
26.
解:(1)①连结AO并延长到Q,连结PA
∵OB,OC分别平分∠ABC,∠ACB,
∴∠ABO=;∠ACO=,
∴∠BOQ=∠ABO+∠BAO,∠QOC=∠OCA+∠OAC,
∴∠BOC=∠BOQ+∠QOC=∠ABO+∠BAO+∠OCA+∠OAC,
∴∠BOC=∠BAC++,
=∠A++,
=∠A+180°-
,
=90°+,
=115°,
BP,CP分别平分∠ABC,∠ACB的外角∠DBC,∠ECB,
∴∠DBP=;∠ECP=,
∠DBP=∠BAP+∠BPA,∠ECP=∠CAP+∠CPA,
∴∠DBP+∠ECP=∠BAP+∠BPA+∠CAP+∠CPA=∠A+∠P,
∴,
∴,
∴90?+,
∴,
故答案为:115?;65?;
②由①得∠O=90°+,
,
∵∠A=α,
∴∠O=90°+,,
故答案为:∠O=90°+,,
解:,
理由如下:
在四边形ABCD中,BP,CP分别平分外角∠EBC,∠FCB,
∴∠CBP=;∠BCP=,
,
,
,
,
;
(3)延长CB,DE交直线AF与M、N如图,
由(2)得,
∴∠M=∠FAB+∠CBA-180?,∠N=∠EFA+∠DEF-180?,
∴∠M+∠N=∠FAB+∠CBA-180?+∠EFA+∠DEF-180?=∠FAB+∠CBA+∠EFA+∠DEF-360?,
∴,
∴,
∴,
故答案为:.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
