北师大版八年级数学下册6.3-6.4三角形的中位线与多边形角度计算一课一练习题2(Word版,含答案)
文档属性
| 名称 | 北师大版八年级数学下册6.3-6.4三角形的中位线与多边形角度计算一课一练习题2(Word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 360.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 22:48:40 | ||
图片预览


文档简介
《三角形中位线与多边形角度计算》习题2
一、选择题
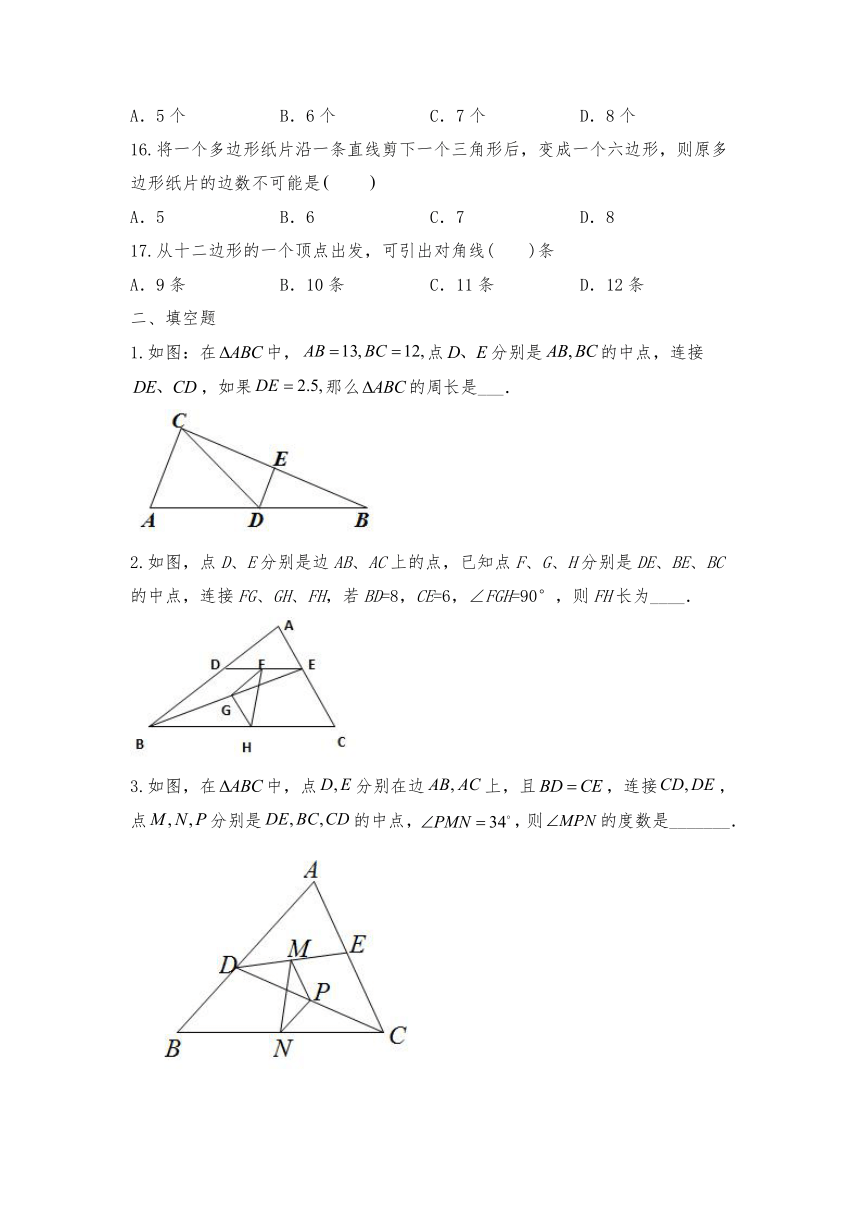
1.如图,在中,是上一点,于点,点是的中点,若,则的长为(
)
A.
B.
C.
D.
2.如图,是的边的中点平分.且,垂足为且,.,则的周长是(
)
A.24
B.25
C.26
D.28
3.如图,已知四边形中,、分别为、上的点,、分别为、的中点.当点在上从点向点移动而点不动时,那么下列结论成立的是(
)
A.线段的长逐渐增大
B.线段的长不变
C.线段的长逐渐减小
D.线段的长与点的位置有关
4.若一个凸多边形的内角和为720°,则这个多边形的边数为
A.4
B.5
C.6
D.7
5.已知一个多边形的内角和是,则这个多边形是(
)
A.四边形
B.五边形
C.六边形
D.七边形
6.如果一个多边形的边数增加1倍,它的内角和是2160°,那么原来的多边形的边数是
(
)
A.5
B.6
C.7
D.8
7.一个多边形的每个内角都等于135°,则这个多边形的边数为(
)
A.5
B.6
C.7
D.8
8.如图,四边形中,过点A的直线l将该四边形分割成两个多边形,若这两个多边形的内角和分别为和,则的度数是(
)
A.
B.
C.
D.
9.一个多边形的每个内角都是120°,这个多边形是(
)
A.四边形
B.六边形
C.八边形
D.十边形
10.一个多边形的内角和比外角和的倍多,则它的边数是(
)
A.八
B.九
C.十
D.十一
11.若多边形的边数增加一条,则它的外角和(
)
A.增加180°
B.不变
C.增加360°
D.减少180°
12.已知一个正多边形的每个外角都等于72°,则这个正多边形是(
)
A.正五边形
B.正六边形
C.正七边形
D.正八边形
13.若一个多边形的外角和与它的内角和相等,则这个多边形是(
)
A.三角形
B.四边形
C.五边形
D.六边形
14.下列多边形中,对角线是5条的多边形是(
)
A.四边形
B.五边形
C.六边形
D.七边形
15.在八边形内任取一点,把这个点与八边形各顶点分别连接可得到几个三角形( )
A.5个
B.6个
C.7个
D.8个
16.将一个多边形纸片沿一条直线剪下一个三角形后,变成一个六边形,则原多边形纸片的边数不可能是
A.5
B.6
C.7
D.8
17.从十二边形的一个顶点出发,可引出对角线(
)条
A.9条
B.10条
C.11条
D.12条
二、填空题
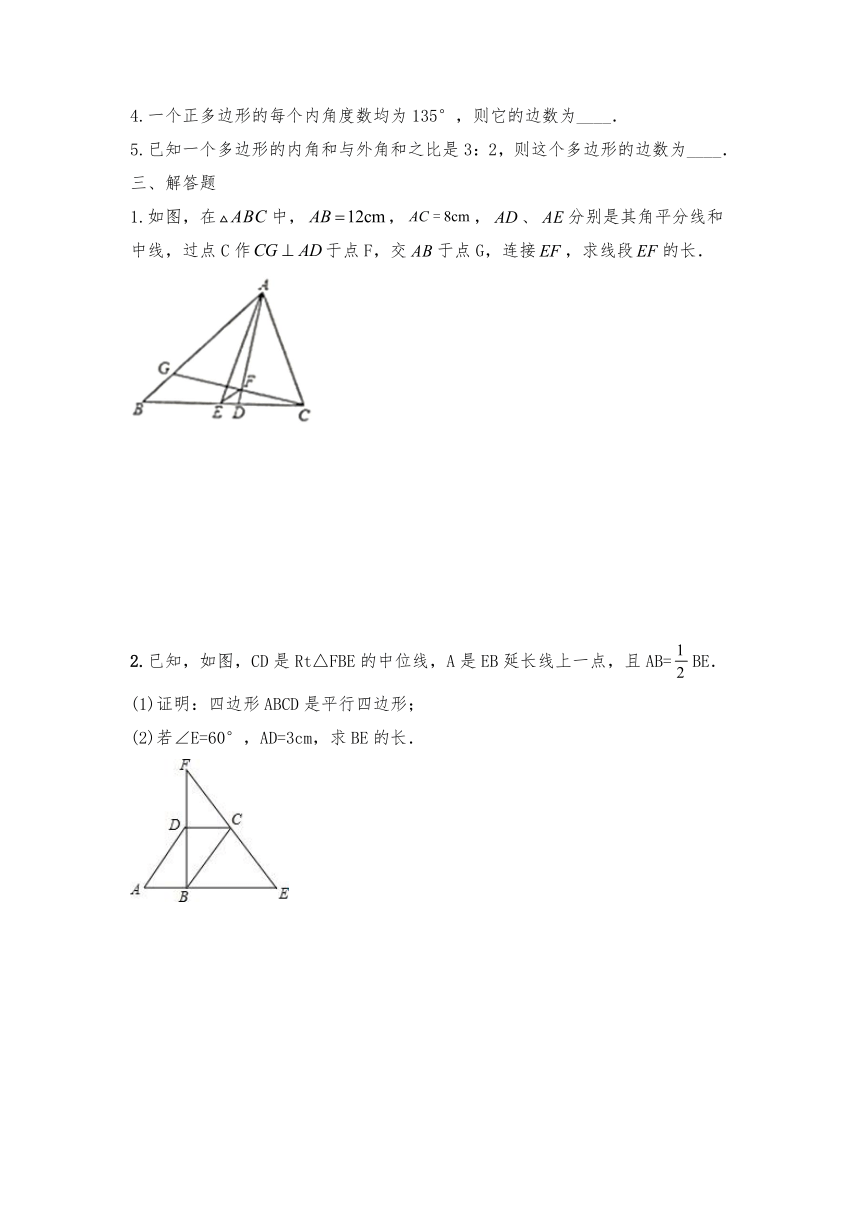
1.如图:在中,点分别是的中点,连接,如果那么的周长是___.
2.如图,点D、E分别是边AB、AC上的点,已知点F、G、H分别是DE、BE、BC的中点,连接FG、GH、FH,若BD=8,CE=6,∠FGH=90°,则FH长为____.
3.如图,在中,点分别在边上,且,连接,点分别是的中点,,则的度数是_______.
4.一个正多边形的每个内角度数均为135°,则它的边数为____.
5.已知一个多边形的内角和与外角和之比是3:2,则这个多边形的边数为____.
三、解答题
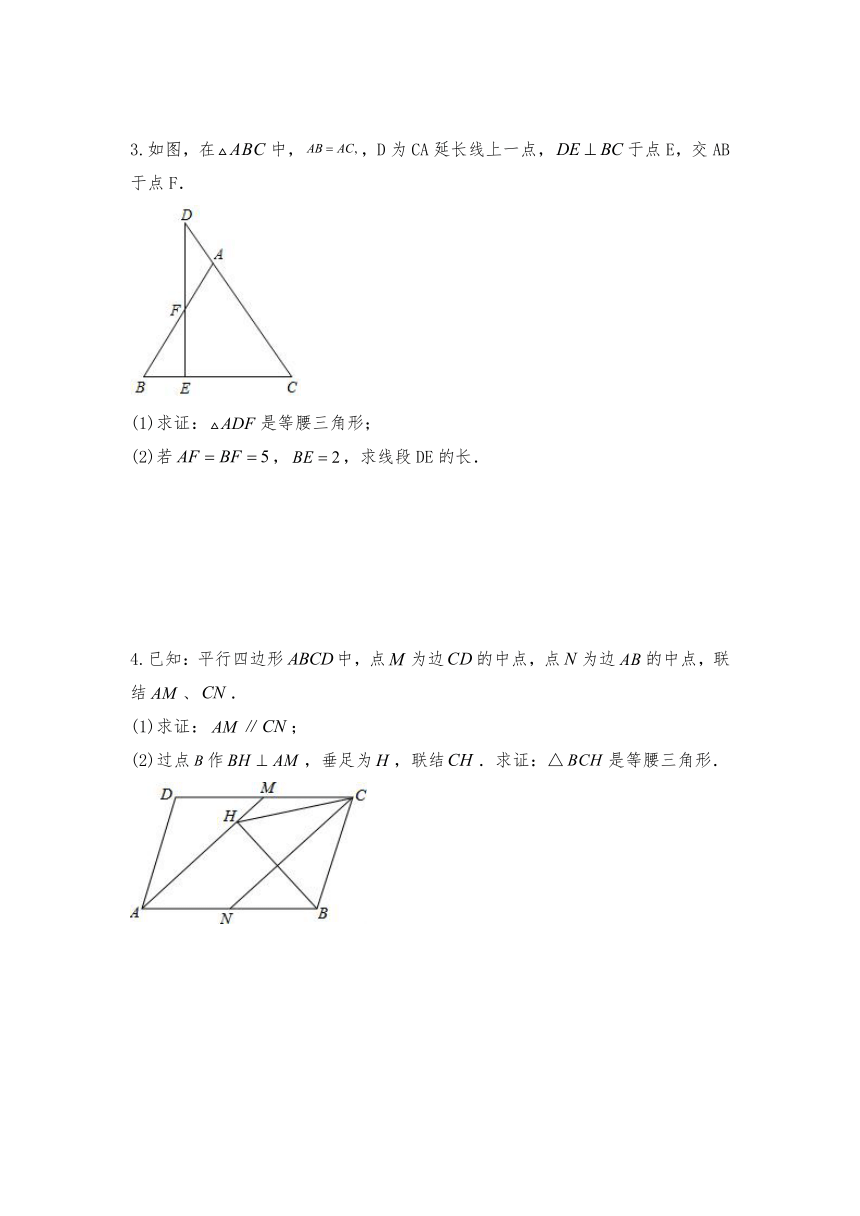
1.如图,在中,,,、分别是其角平分线和中线,过点C作于点F,交于点G,连接,求线段的长.
2.已知,如图,CD是Rt△FBE的中位线,A是EB延长线上一点,且AB=BE.
(1)证明:四边形ABCD是平行四边形;
(2)若∠E=60°,AD=3cm,求BE的长.
3.如图,在中,,D为CA延长线上一点,于点E,交AB于点F.
(1)求证:是等腰三角形;
(2)若,,求线段DE的长.
4.已知:平行四边形中,点为边的中点,点为边的中点,联结、.
(1)求证:∥;
(2)过点作,垂足为,联结.求证:△是等腰三角形.
5.如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是________,位置关系是________;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
6.如果一个多边形的内角和与外角和之比是
13:2,求这个多边形的边数.
7.一个多边形的外角和是它内角和的,求:
(1)这个多边形的边数;
(2)这个多边形共有多少条对角线.
答案
一、选择题
1.C.2.C.3.B.4.C.5.B.6.C.7.D.8.B.9.B.
10.B.11.B.12.A.13.B.14.B.15.D.16.D17.A.
二、填空题
1.30
2.5
3.112?
4.8.
5.5.
三、解答题
1.解:在和中,
,
∴,
∴,
∴,
则().
又∵,
∴是的中位线,
∴.
答:的长为.
2.解:(1)证明:∵CD是Rt△FBE的中位线,
∴CD∥BE,CD=BE,
∴AB=BE,
∴AB=CD,
∴四边形ABCD是平行四边形;
(2)∵四边形ABCD是平行四边形,
∴BC=AD=3cm,
∵CD是Rt△FBE的中位线,
∴BC=CE=EF,
∵∠E=60°,
∴△BCE是等边三角形,
∴BE=BC=3cm.
3.解:(1)∵AB=AC,
∴∠B=∠C,
∵DE⊥BC,
∴∠C+∠D=90°,∠B+∠BFE=90°,
∴∠D=∠BFE,
又∵∠BFE=∠AFD,
∴∠D=∠AFD,
∴AD=AF,即△ADF为等腰三角形;
(2)过A作AH⊥BC,
∵,DE⊥BC,
∴EF//AH,
∴EF是△BAH的中位线,
∵BE=2,
∴EH=2,
∵AB=AC,
∴BC=4BE=8,EC=HC+HE=BH+EH=6,
∵DA=AF=5,AC=AB=10,
∴DC=AD+AC=15,
∴.
4.解:(1)证明:∵四边形是平行四边形,
∴∥且.
∵点、分别是边、的中点,
∴,.
∴.
又∵∥,
∴四边形是平行四边形
∴∥.
(2)设BH与CN交于点E,
∵AM∥CN,BH⊥AM,
∴BH⊥CN,
∵N是AB的中点,
∴EN是△BAH的中位线,
∴BE=EH,
∴CN是BH的垂直平分线,
∴CH=CB,
∴△BCH是等腰三角形.
5.解:(1)∵点P,N是BC,CD的中点,
∴PN∥BD,PN=BD,
∵点P,M是CD,DE的中点,
∴PM∥CE,PM=CE,
∵AB=AC,AD=AE,
∴BD=CE,
∴PM=PN,
∵PN∥BD,
∴∠DPN=∠ADC,
∵PM∥CE,
∴∠DPM=∠DCA,
∵∠BAC=90°,
∴∠ADC+∠ACD=90°,
∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°,
∴PM⊥PN,
故答案为:PM=PN,PM⊥PN;
是等腰直角三角形,理由如下:
由旋转知,,
,
≌,
,
利用三角形的中位线得,,
,
是等腰三角形,
同的方法得,,
,
同的方法得,,
,
,
,
,
,
,
是等腰直角三角形.
6.解:设这个多边形的边数为,依题意得:
,
解得,
这个多边形的边数为15.
7.解:设这个多边形的边数为n,由题意得:
180(n-2)×=360,
解得:n=10,
答:这个多边形的边数为10;
(2)10×(10-3)÷2=35(条).
一、选择题
1.如图,在中,是上一点,于点,点是的中点,若,则的长为(
)
A.
B.
C.
D.
2.如图,是的边的中点平分.且,垂足为且,.,则的周长是(
)
A.24
B.25
C.26
D.28
3.如图,已知四边形中,、分别为、上的点,、分别为、的中点.当点在上从点向点移动而点不动时,那么下列结论成立的是(
)
A.线段的长逐渐增大
B.线段的长不变
C.线段的长逐渐减小
D.线段的长与点的位置有关
4.若一个凸多边形的内角和为720°,则这个多边形的边数为
A.4
B.5
C.6
D.7
5.已知一个多边形的内角和是,则这个多边形是(
)
A.四边形
B.五边形
C.六边形
D.七边形
6.如果一个多边形的边数增加1倍,它的内角和是2160°,那么原来的多边形的边数是
(
)
A.5
B.6
C.7
D.8
7.一个多边形的每个内角都等于135°,则这个多边形的边数为(
)
A.5
B.6
C.7
D.8
8.如图,四边形中,过点A的直线l将该四边形分割成两个多边形,若这两个多边形的内角和分别为和,则的度数是(
)
A.
B.
C.
D.
9.一个多边形的每个内角都是120°,这个多边形是(
)
A.四边形
B.六边形
C.八边形
D.十边形
10.一个多边形的内角和比外角和的倍多,则它的边数是(
)
A.八
B.九
C.十
D.十一
11.若多边形的边数增加一条,则它的外角和(
)
A.增加180°
B.不变
C.增加360°
D.减少180°
12.已知一个正多边形的每个外角都等于72°,则这个正多边形是(
)
A.正五边形
B.正六边形
C.正七边形
D.正八边形
13.若一个多边形的外角和与它的内角和相等,则这个多边形是(
)
A.三角形
B.四边形
C.五边形
D.六边形
14.下列多边形中,对角线是5条的多边形是(
)
A.四边形
B.五边形
C.六边形
D.七边形
15.在八边形内任取一点,把这个点与八边形各顶点分别连接可得到几个三角形( )
A.5个
B.6个
C.7个
D.8个
16.将一个多边形纸片沿一条直线剪下一个三角形后,变成一个六边形,则原多边形纸片的边数不可能是
A.5
B.6
C.7
D.8
17.从十二边形的一个顶点出发,可引出对角线(
)条
A.9条
B.10条
C.11条
D.12条
二、填空题
1.如图:在中,点分别是的中点,连接,如果那么的周长是___.
2.如图,点D、E分别是边AB、AC上的点,已知点F、G、H分别是DE、BE、BC的中点,连接FG、GH、FH,若BD=8,CE=6,∠FGH=90°,则FH长为____.
3.如图,在中,点分别在边上,且,连接,点分别是的中点,,则的度数是_______.
4.一个正多边形的每个内角度数均为135°,则它的边数为____.
5.已知一个多边形的内角和与外角和之比是3:2,则这个多边形的边数为____.
三、解答题
1.如图,在中,,,、分别是其角平分线和中线,过点C作于点F,交于点G,连接,求线段的长.
2.已知,如图,CD是Rt△FBE的中位线,A是EB延长线上一点,且AB=BE.
(1)证明:四边形ABCD是平行四边形;
(2)若∠E=60°,AD=3cm,求BE的长.
3.如图,在中,,D为CA延长线上一点,于点E,交AB于点F.
(1)求证:是等腰三角形;
(2)若,,求线段DE的长.
4.已知:平行四边形中,点为边的中点,点为边的中点,联结、.
(1)求证:∥;
(2)过点作,垂足为,联结.求证:△是等腰三角形.
5.如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是________,位置关系是________;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
6.如果一个多边形的内角和与外角和之比是
13:2,求这个多边形的边数.
7.一个多边形的外角和是它内角和的,求:
(1)这个多边形的边数;
(2)这个多边形共有多少条对角线.
答案
一、选择题
1.C.2.C.3.B.4.C.5.B.6.C.7.D.8.B.9.B.
10.B.11.B.12.A.13.B.14.B.15.D.16.D17.A.
二、填空题
1.30
2.5
3.112?
4.8.
5.5.
三、解答题
1.解:在和中,
,
∴,
∴,
∴,
则().
又∵,
∴是的中位线,
∴.
答:的长为.
2.解:(1)证明:∵CD是Rt△FBE的中位线,
∴CD∥BE,CD=BE,
∴AB=BE,
∴AB=CD,
∴四边形ABCD是平行四边形;
(2)∵四边形ABCD是平行四边形,
∴BC=AD=3cm,
∵CD是Rt△FBE的中位线,
∴BC=CE=EF,
∵∠E=60°,
∴△BCE是等边三角形,
∴BE=BC=3cm.
3.解:(1)∵AB=AC,
∴∠B=∠C,
∵DE⊥BC,
∴∠C+∠D=90°,∠B+∠BFE=90°,
∴∠D=∠BFE,
又∵∠BFE=∠AFD,
∴∠D=∠AFD,
∴AD=AF,即△ADF为等腰三角形;
(2)过A作AH⊥BC,
∵,DE⊥BC,
∴EF//AH,
∴EF是△BAH的中位线,
∵BE=2,
∴EH=2,
∵AB=AC,
∴BC=4BE=8,EC=HC+HE=BH+EH=6,
∵DA=AF=5,AC=AB=10,
∴DC=AD+AC=15,
∴.
4.解:(1)证明:∵四边形是平行四边形,
∴∥且.
∵点、分别是边、的中点,
∴,.
∴.
又∵∥,
∴四边形是平行四边形
∴∥.
(2)设BH与CN交于点E,
∵AM∥CN,BH⊥AM,
∴BH⊥CN,
∵N是AB的中点,
∴EN是△BAH的中位线,
∴BE=EH,
∴CN是BH的垂直平分线,
∴CH=CB,
∴△BCH是等腰三角形.
5.解:(1)∵点P,N是BC,CD的中点,
∴PN∥BD,PN=BD,
∵点P,M是CD,DE的中点,
∴PM∥CE,PM=CE,
∵AB=AC,AD=AE,
∴BD=CE,
∴PM=PN,
∵PN∥BD,
∴∠DPN=∠ADC,
∵PM∥CE,
∴∠DPM=∠DCA,
∵∠BAC=90°,
∴∠ADC+∠ACD=90°,
∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°,
∴PM⊥PN,
故答案为:PM=PN,PM⊥PN;
是等腰直角三角形,理由如下:
由旋转知,,
,
≌,
,
利用三角形的中位线得,,
,
是等腰三角形,
同的方法得,,
,
同的方法得,,
,
,
,
,
,
,
是等腰直角三角形.
6.解:设这个多边形的边数为,依题意得:
,
解得,
这个多边形的边数为15.
7.解:设这个多边形的边数为n,由题意得:
180(n-2)×=360,
解得:n=10,
答:这个多边形的边数为10;
(2)10×(10-3)÷2=35(条).
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
