2021--2022学年沪科版七年级数学上册 4.5 角的比较与补(余)角课件( 第一课时 共24张)
文档属性
| 名称 | 2021--2022学年沪科版七年级数学上册 4.5 角的比较与补(余)角课件( 第一课时 共24张) |

|
|
| 格式 | zip | ||
| 文件大小 | 293.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 00:00:00 | ||
图片预览



文档简介
(共24张PPT)
沪科版数学七年级(上)
第4章
直线与角
4.5角的比较与补(余)角
第一课时
知识回顾:比较两条线段的长短方法?
1、度量法:以“数”
出发,用刻度尺测量线段的长度的方法。
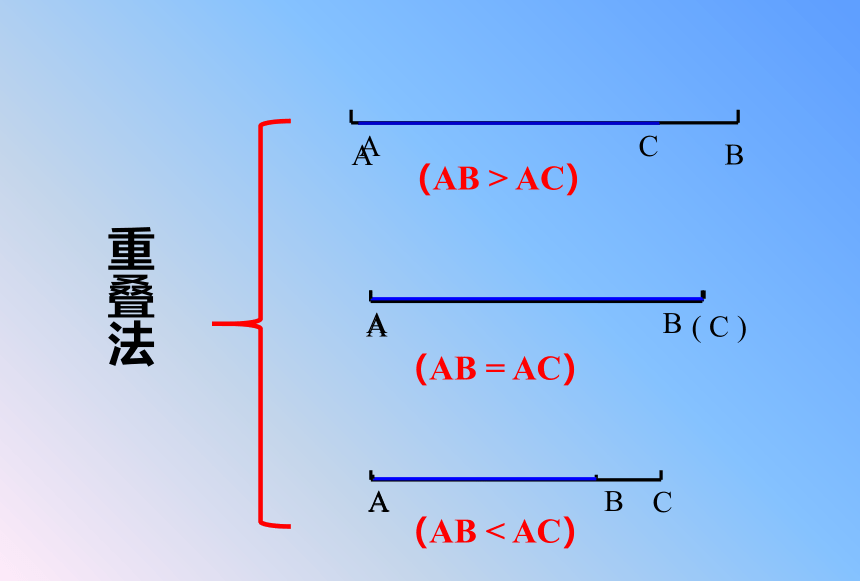
2、重叠法:将其中一条线段移到另一条线段上作比较。
5
cm
A
B
3
cm
C
D
AB
>
CD
重叠法
A
(
C
)
A
C
A
B
C
A
A
B
A
B
(AB
>
AC)
(AB
=
AC)
(AB
<
AC)
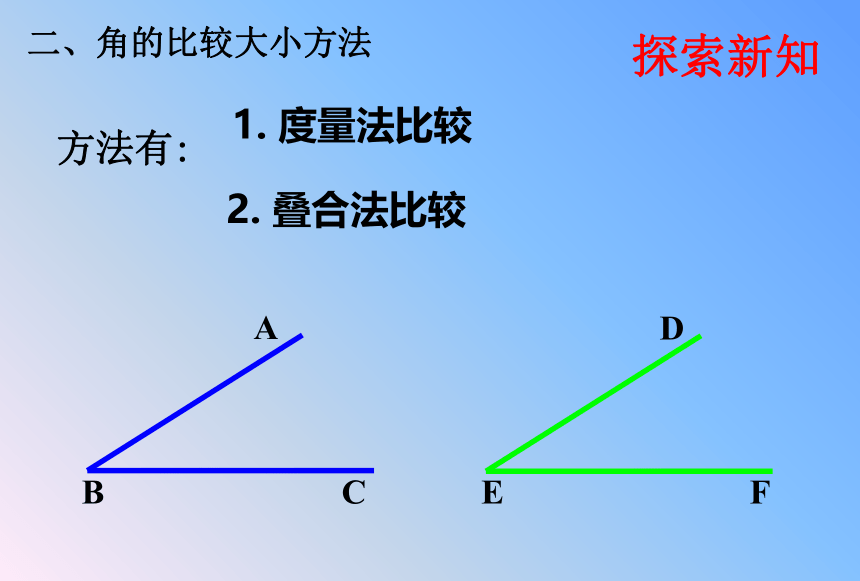
二、角的比较大小方法
B
A
C
E
D
F
方法有:
1.
度量法比较
2.
叠合法比较
探索新知
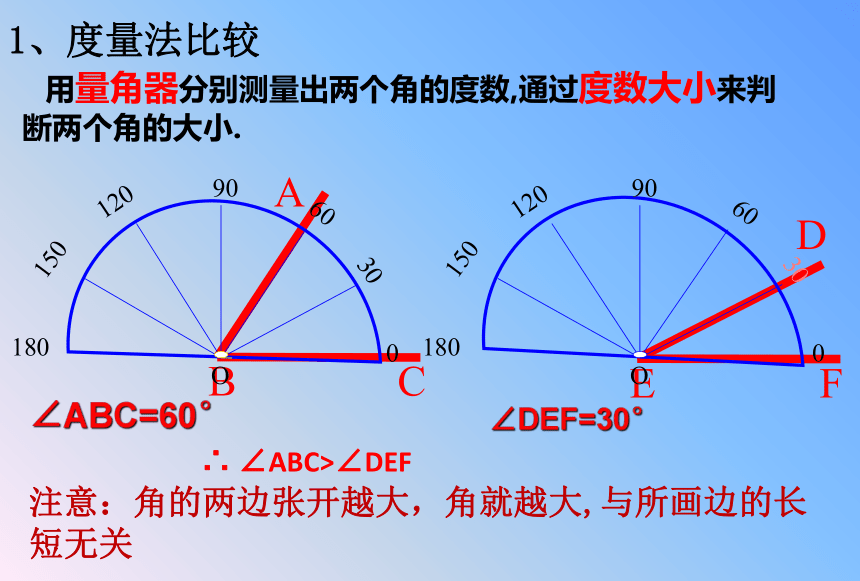
1、度量法比较
C
A
B
O
30
0
60
90
120
150
180
∠ABC=60°
F
D
E
O
30
0
60
90
120
150
180
∠DEF=30°
∴
∠ABC>∠DEF
用量角器分别测量出两个角的度数,通过度数大小来判断两个角的大小.
注意:角的两边张开越大,角就越大,与所画边的长短无关
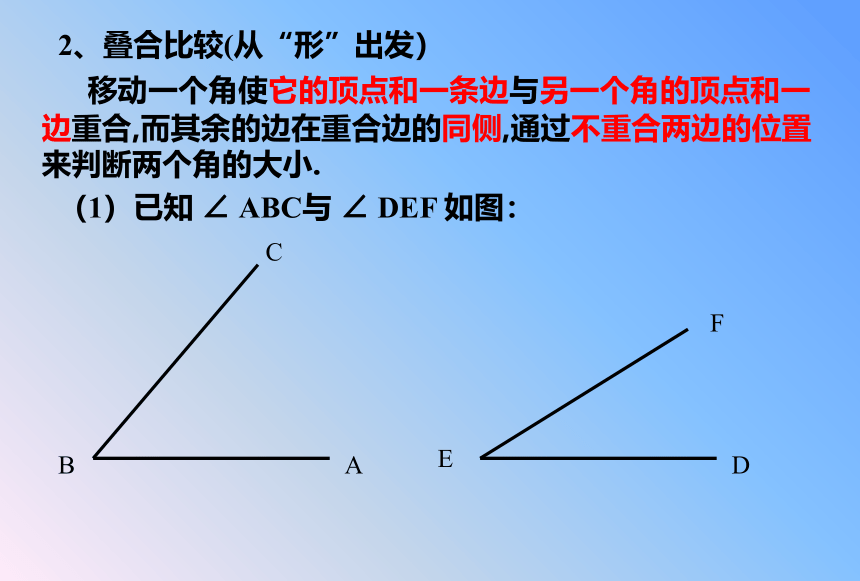
2、叠合比较(从“形”出发)
(1)已知
∠
ABC与
∠
DEF
如图:
D
E
F
A
B
C
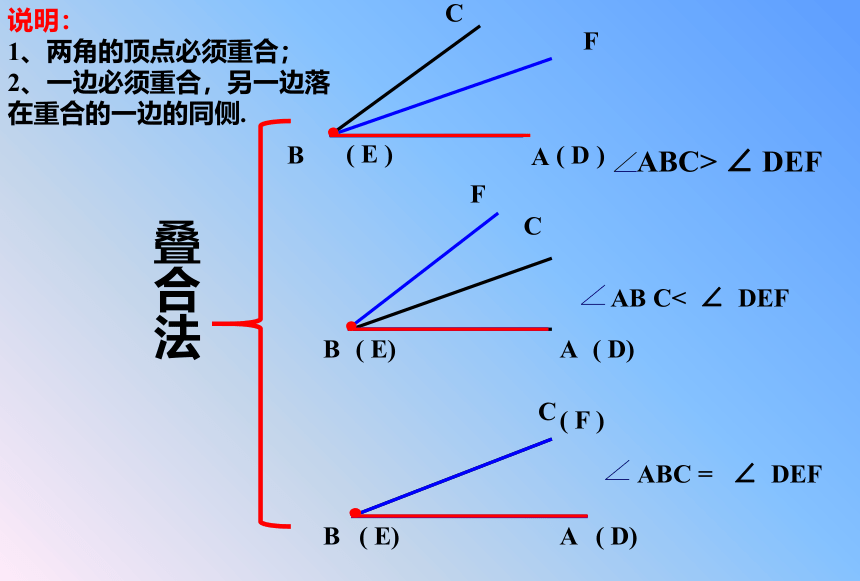
移动一个角使它的顶点和一条边与另一个角的顶点和一边重合,而其余的边在重合边的同侧,通过不重合两边的位置来判断两个角的大小.
A
B
C
F
(
E)
(
D)
A
B
C
(
E)
(
D)
(
F
)
A
B
C
F
(
E
)
(
D
)
叠合法
ABC>
∠
DEF
AB
C<
∠
DEF
ABC
=
∠
DEF
说明:
1、两角的顶点必须重合;
2、一边必须重合,另一边落
在重合的一边的同侧.
二、角的和差
已知两个角
∠
1和
∠
2(
∠
1
>
∠2
),把它们的顶点和一边重合。
1
2
A
O
B
B
O
C
探索新知
1
O
A
B
2
C
B
O
A
1
B
O
O
B
C
2
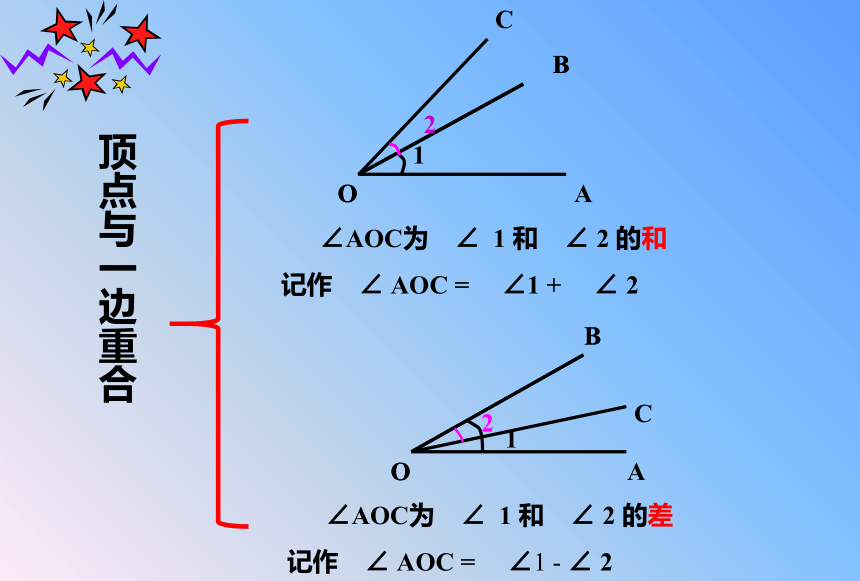
顶点与一边重合
∠AOC为
∠
1
和
∠
2
的和
记作
∠
AOC
=
∠1
+
∠
2
∠AOC为
∠
1
和
∠
2
的差
记作
∠
AOC
=
∠1
-
∠
2
1、如图,用〝=〞或
〝>〞或
〝<〞填空
D
O
C
B
A
=
>
=
<
=
练一练
∵∠AOC=∠AOB+∠BOC
∠BOD=∠COD
+
∠BOC
∴∠AOC=BOD
1、图中共有几个角?它们之间有什么关系?
答:有三个角,关系是:
∠BOC是
∠AOC与
∠AOB的差,记作
∠BOC=∠AOC-∠AOB.
∠AOC是∠AOB与
∠BOC的和,记作
∠AOC=∠AOB+∠BOC,
∠AOB是
∠AOC与
∠BOC的差,记作
∠AOB=∠AOC-∠BOC,
练习巩固,应用新知
2、如图,已知∠AOC=67°,∠BOC=22°,求∠AOB的度数
解:
∵
∠AOC=67°,∠BOC=22°
∴∠AOB=∠AOC-∠BOC
=67°—22°
=45°
2、如图,已知∠AOB=45°,∠BOC=22°,求∠AOC的度数
活动:折一折
在纸上画一个角并剪下,将它对折使其两边重合,折痕与角两边所成的两个角的大小关系怎样?
三、角平分线
探索新知
2
1
2
1
B
A
C
O
角的平分线定义:
在角的内部,自角的顶点引一条射线把
这个角分成两个相等的角,那么这条射线叫做角的平分线。
角平分线定义:
当
∠1
=
∠
2
时,射线OB
把
∠AOC分成两个相等的角,
这时OB叫做
∠AOC
的平
分线,也可以说OB平分
∠
AOC
角平分线的几何意义
⌒
3
1
O
A
C
B
∵∠1=∠3
(或∠AOB=
2∠1
,
∠AOB=
2∠3)
∴射线OC平分∠AOB
∵射线OC平分∠AOB
∴∠1=∠3
(或∠AOB=
2∠1
,
∠2=
2∠3)
⌒
A
B
C
D
E
AD是
BAC的平分线
=
ABC
=
2
ABE
平分
(
角平分线的定义
)
BAD
CAD
BE
ABC
(
角平分线的定义
)
练一练
例1、如图:OC、OD分别是∠AOB
、∠BOE的平分线,
(1)如果∠AOB=700,
∠BOE=600,那么∠1+
∠2=--------
(2)
如果∠1+
∠2
=550,则∠AOE=
--------
A
O
B
C
E
D
1
2
650
1100
O
A
B
D
C
E
例2、如图,点O在直线AB上,OD、OE分别是∠AOC
、∠BOC的平分线,求∠EOD的度数
已知O为直线AB上一点,OE平分∠AOC,OF平分
∠COB,求∠EOF的大小?
思考:
解:
∵
OE平分
∠
AOC,OF平分
∠COB
∴∠EOF=∠EOC+∠COF
=1/2∠AOC+1/2∠COB
=1/2(∠AOC+∠COB)
=90°
∴∠EOC=1/2∠AOC,
∠COF=1/2∠COB
(角平分线的定义)
∵∠AOB=∠AOC+∠COB=180°
(平角的定义)
A
B
E
C
F
O
1.如图,OB平分∠COD,∠AOB=90°,
∠AOC=125°,求∠COD的度数。
∠BOC=
∴∠BOD=∠BOC
=35°
∴∠COD=35°×2=70°
D
B
C
O
A
∠AOC-∠AOB
=125°-90°
解:
=35°
∵OB平分∠COD
强化练习
2.如图,OC平分∠AOD,∠BOD=2∠AOB.若∠AOD=114°,求∠BOC的度数?
A
B
C
D
O
=57°-38°
=19°
解:
强化练习
利用一副三角板,你能画出哪些度数的角?这
些角有什么规律?
拓展:
30°、45°、60°、90°、
15°、75°、105°、120°、135°、150°、165°、
180°
实践活动:请你试用一对三角尺根据刚才
学过的角的和差知识拼出所有的特殊角。
可以拼出15°的整倍数的角.
课堂小结
1、角的大小比较方法
2、角的和与差
3、角的平分线
度量法
叠合法
在角的内部,自角的顶点引一条射线把
这个角分成两个相等的角,那么这条射线叫做角的平分线。
沪科版数学七年级(上)
第4章
直线与角
4.5角的比较与补(余)角
第一课时
知识回顾:比较两条线段的长短方法?
1、度量法:以“数”
出发,用刻度尺测量线段的长度的方法。
2、重叠法:将其中一条线段移到另一条线段上作比较。
5
cm
A
B
3
cm
C
D
AB
>
CD
重叠法
A
(
C
)
A
C
A
B
C
A
A
B
A
B
(AB
>
AC)
(AB
=
AC)
(AB
<
AC)
二、角的比较大小方法
B
A
C
E
D
F
方法有:
1.
度量法比较
2.
叠合法比较
探索新知
1、度量法比较
C
A
B
O
30
0
60
90
120
150
180
∠ABC=60°
F
D
E
O
30
0
60
90
120
150
180
∠DEF=30°
∴
∠ABC>∠DEF
用量角器分别测量出两个角的度数,通过度数大小来判断两个角的大小.
注意:角的两边张开越大,角就越大,与所画边的长短无关
2、叠合比较(从“形”出发)
(1)已知
∠
ABC与
∠
DEF
如图:
D
E
F
A
B
C
移动一个角使它的顶点和一条边与另一个角的顶点和一边重合,而其余的边在重合边的同侧,通过不重合两边的位置来判断两个角的大小.
A
B
C
F
(
E)
(
D)
A
B
C
(
E)
(
D)
(
F
)
A
B
C
F
(
E
)
(
D
)
叠合法
ABC>
∠
DEF
AB
C<
∠
DEF
ABC
=
∠
DEF
说明:
1、两角的顶点必须重合;
2、一边必须重合,另一边落
在重合的一边的同侧.
二、角的和差
已知两个角
∠
1和
∠
2(
∠
1
>
∠2
),把它们的顶点和一边重合。
1
2
A
O
B
B
O
C
探索新知
1
O
A
B
2
C
B
O
A
1
B
O
O
B
C
2
顶点与一边重合
∠AOC为
∠
1
和
∠
2
的和
记作
∠
AOC
=
∠1
+
∠
2
∠AOC为
∠
1
和
∠
2
的差
记作
∠
AOC
=
∠1
-
∠
2
1、如图,用〝=〞或
〝>〞或
〝<〞填空
D
O
C
B
A
=
>
=
<
=
练一练
∵∠AOC=∠AOB+∠BOC
∠BOD=∠COD
+
∠BOC
∴∠AOC=BOD
1、图中共有几个角?它们之间有什么关系?
答:有三个角,关系是:
∠BOC是
∠AOC与
∠AOB的差,记作
∠BOC=∠AOC-∠AOB.
∠AOC是∠AOB与
∠BOC的和,记作
∠AOC=∠AOB+∠BOC,
∠AOB是
∠AOC与
∠BOC的差,记作
∠AOB=∠AOC-∠BOC,
练习巩固,应用新知
2、如图,已知∠AOC=67°,∠BOC=22°,求∠AOB的度数
解:
∵
∠AOC=67°,∠BOC=22°
∴∠AOB=∠AOC-∠BOC
=67°—22°
=45°
2、如图,已知∠AOB=45°,∠BOC=22°,求∠AOC的度数
活动:折一折
在纸上画一个角并剪下,将它对折使其两边重合,折痕与角两边所成的两个角的大小关系怎样?
三、角平分线
探索新知
2
1
2
1
B
A
C
O
角的平分线定义:
在角的内部,自角的顶点引一条射线把
这个角分成两个相等的角,那么这条射线叫做角的平分线。
角平分线定义:
当
∠1
=
∠
2
时,射线OB
把
∠AOC分成两个相等的角,
这时OB叫做
∠AOC
的平
分线,也可以说OB平分
∠
AOC
角平分线的几何意义
⌒
3
1
O
A
C
B
∵∠1=∠3
(或∠AOB=
2∠1
,
∠AOB=
2∠3)
∴射线OC平分∠AOB
∵射线OC平分∠AOB
∴∠1=∠3
(或∠AOB=
2∠1
,
∠2=
2∠3)
⌒
A
B
C
D
E
AD是
BAC的平分线
=
ABC
=
2
ABE
平分
(
角平分线的定义
)
BAD
CAD
BE
ABC
(
角平分线的定义
)
练一练
例1、如图:OC、OD分别是∠AOB
、∠BOE的平分线,
(1)如果∠AOB=700,
∠BOE=600,那么∠1+
∠2=--------
(2)
如果∠1+
∠2
=550,则∠AOE=
--------
A
O
B
C
E
D
1
2
650
1100
O
A
B
D
C
E
例2、如图,点O在直线AB上,OD、OE分别是∠AOC
、∠BOC的平分线,求∠EOD的度数
已知O为直线AB上一点,OE平分∠AOC,OF平分
∠COB,求∠EOF的大小?
思考:
解:
∵
OE平分
∠
AOC,OF平分
∠COB
∴∠EOF=∠EOC+∠COF
=1/2∠AOC+1/2∠COB
=1/2(∠AOC+∠COB)
=90°
∴∠EOC=1/2∠AOC,
∠COF=1/2∠COB
(角平分线的定义)
∵∠AOB=∠AOC+∠COB=180°
(平角的定义)
A
B
E
C
F
O
1.如图,OB平分∠COD,∠AOB=90°,
∠AOC=125°,求∠COD的度数。
∠BOC=
∴∠BOD=∠BOC
=35°
∴∠COD=35°×2=70°
D
B
C
O
A
∠AOC-∠AOB
=125°-90°
解:
=35°
∵OB平分∠COD
强化练习
2.如图,OC平分∠AOD,∠BOD=2∠AOB.若∠AOD=114°,求∠BOC的度数?
A
B
C
D
O
=57°-38°
=19°
解:
强化练习
利用一副三角板,你能画出哪些度数的角?这
些角有什么规律?
拓展:
30°、45°、60°、90°、
15°、75°、105°、120°、135°、150°、165°、
180°
实践活动:请你试用一对三角尺根据刚才
学过的角的和差知识拼出所有的特殊角。
可以拼出15°的整倍数的角.
课堂小结
1、角的大小比较方法
2、角的和与差
3、角的平分线
度量法
叠合法
在角的内部,自角的顶点引一条射线把
这个角分成两个相等的角,那么这条射线叫做角的平分线。
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
