2021-2022学年七年级数学沪科版上册4.5角的比较与补(余)角课件(第二课时 共26张)
文档属性
| 名称 | 2021-2022学年七年级数学沪科版上册4.5角的比较与补(余)角课件(第二课时 共26张) |

|
|
| 格式 | zip | ||
| 文件大小 | 380.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 22:56:15 | ||
图片预览




文档简介
(共26张PPT)
沪科版数学七年级(上)
第4章
直线与角
4.5角的比较与补(余)角
第二课时
余角与补角
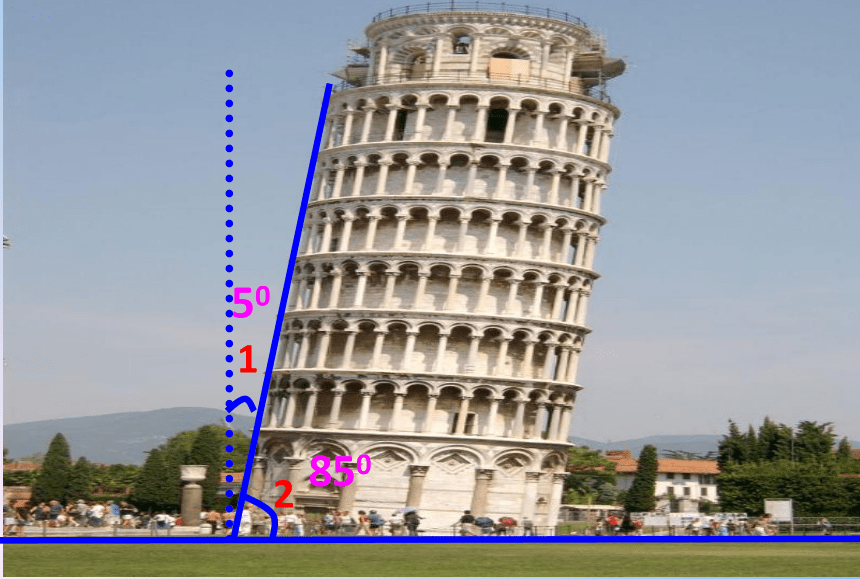
850
1
2
50
2
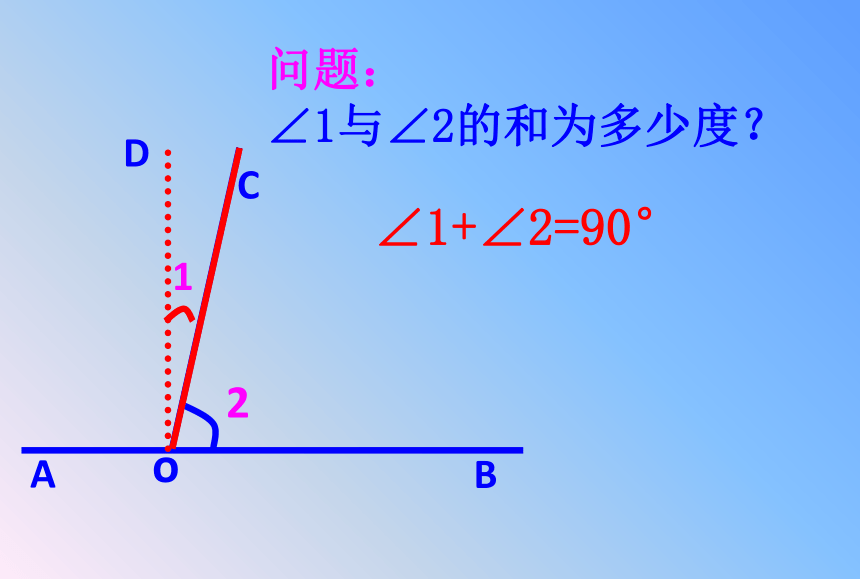
问题:
∠1与∠2的和为多少度?
∠1+∠2=90°
A
B
C
o
1
D
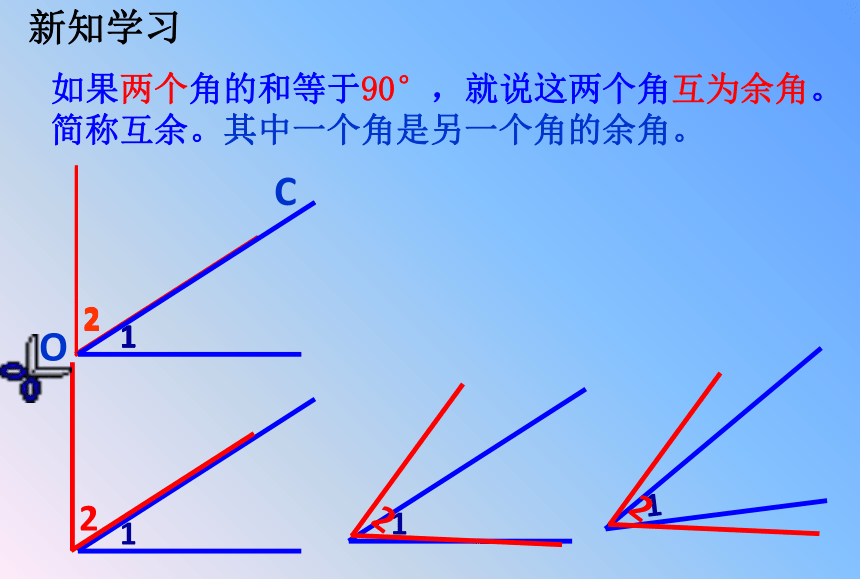
如果两个角的和等于90°,就说这两个角互为余角。简称互余。其中一个角是另一个角的余角。
1
2
1
2
1
1
2
1
2
1
2
C
O
新知学习
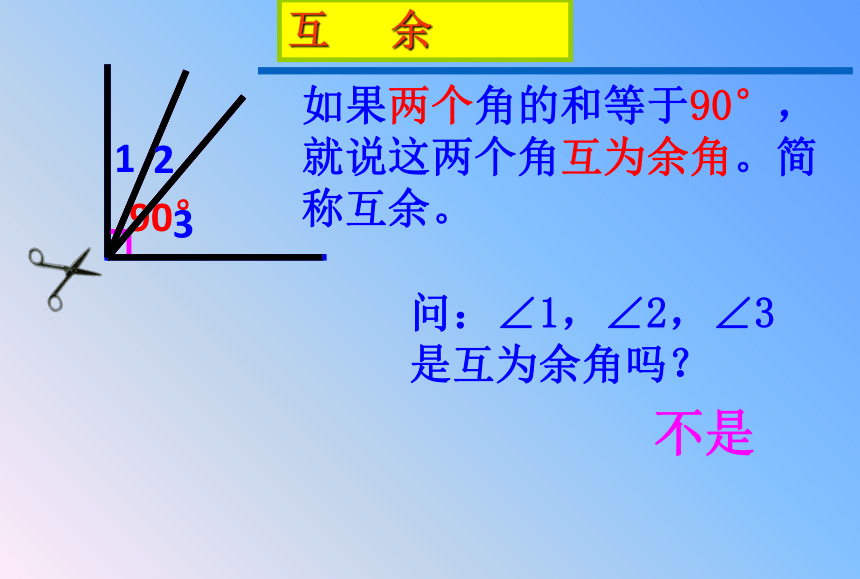
90°
1
2
问:∠1,∠2,∠3
是互为余角吗?
如果两个角的和等于90°,就说这两个角互为余角。简称互余。
不是
3
互
余
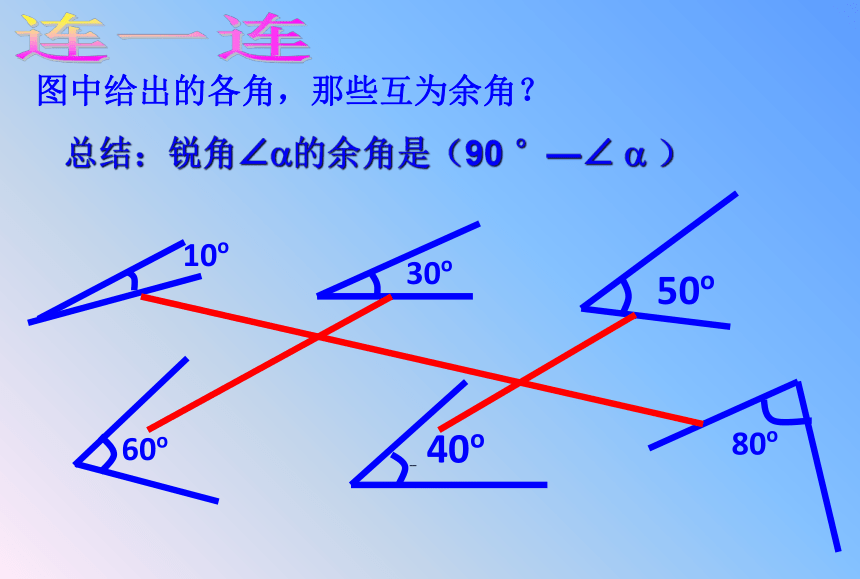
连一连
图中给出的各角,那些互为余角?
10o
30o
60o
80o
50o
40o
总结:锐角∠?的余角是(90
°—∠
?
)
1、若∠1=46°,则它的余角为
。
2、若∠A=25°18′,则它的余角
为
。
变式练习:
变式1:若∠1的余角为54°,则∠1=
。
变式2:若∠1的余角等于它本身的度数,
则∠1=
。
44°
64°42′
36°
45°
新知练习
85o
2
?
1
问题:
∠1与∠2的和为多少度?
∠1+∠2=180°
2
互为补角
如果两个角的和等于180°,就说这两个角互为补角,简称互补。其中一个是另一个角的补角。
新知学习
图中给出的各角,那些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
∠?的补角是(180
°—∠
?
)
连一连
1、若∠1=46°,则它的补角为
。
2、若∠A=25°18′,则它的补角
为
。
变式练习:
变式1:若∠1的补角为54°,则∠1=
。
变式2:若∠1的补角等于它本身的度数,
则∠1=
。
变式3:已知∠A=50°,则∠A的余角是
___
,补角是
___
,补角与余角的差是
___
。
134°
154°42′
126°
90°
40°
130°
90°
新知练习
帮
找朋友
例1、一个角的补角是它的余角的4倍,求这个
角的余角是多少度?
解:设这个角的度数为
,则依题意得
答:这个角的余角的度数为
解决问题
解法一
解:设这个角的余角的度数为
,
则它的补角可设为
答:这个角的余角的度数为
解法二
讨论:
(1)已知∠1与∠2,∠3都互为余角.那么∠2和∠3的大小有什么关系?
∵∠1与∠2,
∠1
与∠3都互为余角,
∴∠2=90?-∠1,
∠3=90?-∠1,
∴∠2=∠3.
余角和补角的性质
思考:已知∠1与∠2互余,∠3与∠4互余,如果∠1=∠3那么∠2与∠4有什么关系?
新知学习
余角的性质
同角或等角的余角相等
讨
论:
(1)已知∠1与∠2,∠3都互为补角.那么∠2和∠3的大小有什么关系?
∵∠1与∠2和∠3都互为补角,
∴∠2=180?-∠1,
∠3=180?-∠1,
∴∠2=∠3.
余角和补角的性质
新知学习
如图∠1
与∠2互补,∠3
与∠4互补
,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
3
2
4
4
2
同角或等角的补角相等
讨论
补角性质
(2)图中哪几对角是相等的角(直角除外)?
说明它们相等的原因。
(1)图中有哪几对互余的角?
∠A与∠B互余
∠A与∠2互余
∠1与∠B互余
∠1与∠2互余
∠B=∠2
∠A=∠1
B
A
D
C
1
2
(同角的余角相等)
(同角的余角相等)
认真观察下面的图形,回答下列问题:
辨一辨
如图,已知∠AOB=90°,
∠AOC=
∠BOD,
则与∠AOC互余的角为_____________.
辨一辨
例2、
如图,∠AOC和∠BOD都是直角。
若∠DOC=28°,求∠AOB的度数。
A
B
C
D
O
新知应用
D
E
O
C
A
B
如图,点O在直线AB上,OD平分∠COA
,OE平分∠COB,
①
∠COB
+∠
AOC=
°,∠
EOD=
°。
②图中互余角有
对,互补角有
对。
4
5
找一找
180
90
课堂小结
1、余角、补角的概念
2、余角、补角的性质
3、类比的数学思想方法
互为余角
互为补角
对
应
图
形
数量关系
性
质
1
2
1
2
∠1+
∠2
=
90
°
∠1+
∠2
=
180
°
等角的余角
相等
等角的补角
相等
同一个角的补角比它的余角大
90°
(
0<
X
<
90
)
互余、互补是两角之间的数量关系,只与他们的度数和有关,与位置无关。
1
互余、互补概念中的角是成对出现的。
2
只有锐角才有余角。
4
注意点
角
的余角是
,补角是
同一个锐角的补角比余角大
3
5
同角的余角(补角)相等;
等角的余角(补角)相等。
沪科版数学七年级(上)
第4章
直线与角
4.5角的比较与补(余)角
第二课时
余角与补角
850
1
2
50
2
问题:
∠1与∠2的和为多少度?
∠1+∠2=90°
A
B
C
o
1
D
如果两个角的和等于90°,就说这两个角互为余角。简称互余。其中一个角是另一个角的余角。
1
2
1
2
1
1
2
1
2
1
2
C
O
新知学习
90°
1
2
问:∠1,∠2,∠3
是互为余角吗?
如果两个角的和等于90°,就说这两个角互为余角。简称互余。
不是
3
互
余
连一连
图中给出的各角,那些互为余角?
10o
30o
60o
80o
50o
40o
总结:锐角∠?的余角是(90
°—∠
?
)
1、若∠1=46°,则它的余角为
。
2、若∠A=25°18′,则它的余角
为
。
变式练习:
变式1:若∠1的余角为54°,则∠1=
。
变式2:若∠1的余角等于它本身的度数,
则∠1=
。
44°
64°42′
36°
45°
新知练习
85o
2
?
1
问题:
∠1与∠2的和为多少度?
∠1+∠2=180°
2
互为补角
如果两个角的和等于180°,就说这两个角互为补角,简称互补。其中一个是另一个角的补角。
新知学习
图中给出的各角,那些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
∠?的补角是(180
°—∠
?
)
连一连
1、若∠1=46°,则它的补角为
。
2、若∠A=25°18′,则它的补角
为
。
变式练习:
变式1:若∠1的补角为54°,则∠1=
。
变式2:若∠1的补角等于它本身的度数,
则∠1=
。
变式3:已知∠A=50°,则∠A的余角是
___
,补角是
___
,补角与余角的差是
___
。
134°
154°42′
126°
90°
40°
130°
90°
新知练习
帮
找朋友
例1、一个角的补角是它的余角的4倍,求这个
角的余角是多少度?
解:设这个角的度数为
,则依题意得
答:这个角的余角的度数为
解决问题
解法一
解:设这个角的余角的度数为
,
则它的补角可设为
答:这个角的余角的度数为
解法二
讨论:
(1)已知∠1与∠2,∠3都互为余角.那么∠2和∠3的大小有什么关系?
∵∠1与∠2,
∠1
与∠3都互为余角,
∴∠2=90?-∠1,
∠3=90?-∠1,
∴∠2=∠3.
余角和补角的性质
思考:已知∠1与∠2互余,∠3与∠4互余,如果∠1=∠3那么∠2与∠4有什么关系?
新知学习
余角的性质
同角或等角的余角相等
讨
论:
(1)已知∠1与∠2,∠3都互为补角.那么∠2和∠3的大小有什么关系?
∵∠1与∠2和∠3都互为补角,
∴∠2=180?-∠1,
∠3=180?-∠1,
∴∠2=∠3.
余角和补角的性质
新知学习
如图∠1
与∠2互补,∠3
与∠4互补
,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
3
2
4
4
2
同角或等角的补角相等
讨论
补角性质
(2)图中哪几对角是相等的角(直角除外)?
说明它们相等的原因。
(1)图中有哪几对互余的角?
∠A与∠B互余
∠A与∠2互余
∠1与∠B互余
∠1与∠2互余
∠B=∠2
∠A=∠1
B
A
D
C
1
2
(同角的余角相等)
(同角的余角相等)
认真观察下面的图形,回答下列问题:
辨一辨
如图,已知∠AOB=90°,
∠AOC=
∠BOD,
则与∠AOC互余的角为_____________.
辨一辨
例2、
如图,∠AOC和∠BOD都是直角。
若∠DOC=28°,求∠AOB的度数。
A
B
C
D
O
新知应用
D
E
O
C
A
B
如图,点O在直线AB上,OD平分∠COA
,OE平分∠COB,
①
∠COB
+∠
AOC=
°,∠
EOD=
°。
②图中互余角有
对,互补角有
对。
4
5
找一找
180
90
课堂小结
1、余角、补角的概念
2、余角、补角的性质
3、类比的数学思想方法
互为余角
互为补角
对
应
图
形
数量关系
性
质
1
2
1
2
∠1+
∠2
=
90
°
∠1+
∠2
=
180
°
等角的余角
相等
等角的补角
相等
同一个角的补角比它的余角大
90°
(
0<
X
<
90
)
互余、互补是两角之间的数量关系,只与他们的度数和有关,与位置无关。
1
互余、互补概念中的角是成对出现的。
2
只有锐角才有余角。
4
注意点
角
的余角是
,补角是
同一个锐角的补角比余角大
3
5
同角的余角(补角)相等;
等角的余角(补角)相等。
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
