八年级数学下册试题 一课一练 5.4《分式方程》习题2-北师大版(word版含答案)
文档属性
| 名称 | 八年级数学下册试题 一课一练 5.4《分式方程》习题2-北师大版(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 180.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-12 08:00:19 | ||
图片预览



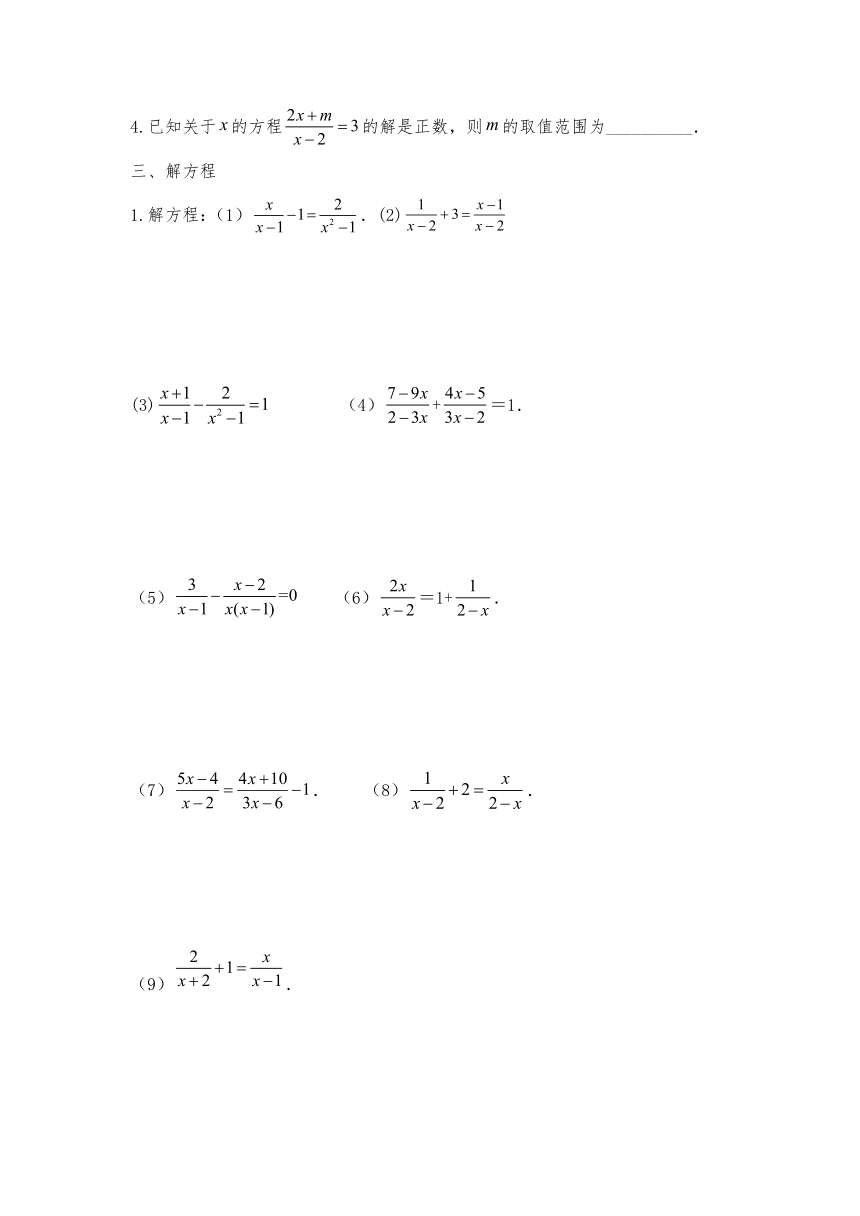
文档简介
5.4《分式方程》习题2
一、选择题
1.将方程去分母化简后,得到的方程是(
)
A.x﹣4=3﹣2
B.x﹣4=3﹣2x+1
C.x﹣4=3﹣2x+2
D.x﹣4=3﹣2x﹣2
2.方程=的解为(
)
A.x=3
B.x=4
C.x=5
D.x=﹣5
3.把分式方程
+
2
=化为整式方程,得( )
A.x+2=2x(x+2)
B.x+2(x2﹣4)=2x(x+2)
C.x+2(x﹣2)=2x(x﹣2)
D.x+2(x2﹣4)=2x(x﹣2)
4.解分式方程,分以下四步,其中错误的一步是(
)
A.方程两边各分式的最简公分母是
B.方程两边都乘以,得整式方程:
C.解这个整式方程,得
D.原方程的解为
5.若数
a使关于
x的分式方程有整数解,且关于y
的不等式组恰
好有两个奇数解,则符合条件的所有整数
a的和是(
)
A.7
B.5
C.2
D.1
6.若整数使得关于的方程的解为非负整数,且关于的不等式组至少有2个整数解,则所有符合条件的整数的和为(
)
A.6
B.9
C.13
D.16
7.关于的分式方程解为,则常数的值为(
).
A.
B.
C.
D.
8.已知关于x的分式方程+=1的解是非负数,则m的取值范围是(
)
A.m>2
B.m≥2
C.m≥2且m≠3
D.m>2且m≠3
9.为了帮助遭受自然灾害的地区重建家园,某学校号召同学们自愿捐款.已知第一次捐款总额为4
800元,第二次捐款总额为5
000元,第二次捐款人数比第一次多20人,而且两次人均捐款额恰好相等.如果设第一次捐款人数为x人,那么x满足的方程是(
)
A.
B.
C.
D.
10.某电子元件厂准备生产4600个电子元件,甲车间独立生产了一半后,由于要尽快投入市场,乙车间也加入该电子元件的生产,若乙车间每天生产的电子元件是甲车间的1.3倍,结果用33天完成任务,问甲车间每天生产电子元件多少个?在这个问题中设甲车间每天生产电子元件x个,根据题意可得方程为
A.
B.
C.
D.
11.八年级学生去距学校10千米的博物馆参观,一部分学生骑自行车先走,过了20分钟后,其余学生乘汽车出发,结果他们同时到达,已知汽车的速度是骑车学生速度的2倍.设骑车学生的速度为x千米/小时,则所列方程正确的是( )
A.-=20
B.-=20
C.-=
D.=
12.某口罩生产企业最近要紧急完成1000万只口罩生产的任务,在生产完400万只口罩后,新的生产线安装完毕,可以加入生产了;新的生产线加入后,每天口罩的生产总量比原来增加了,结果共用了8天完成了任务设新生产线加入前,每天生产口罩万只,则根据题意可得方程为(
)
A.
B.
C.
D.
13.现代互联网技术的广泛应用,催生了快递行业的高速发展.据调查,湘潭某家小型快递公司的分拣工小李和小江,在分拣同一类物件时,小李分拣120个物件所用的时间与小江分拣90个物件所用的时间相同,已知小李每小时比小江多分拣20个物件.若设小江每小时分拣个物件,则可列方程为( )
A.
B.
C.
D.
14.A,B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运40千克,A型机器人搬运1200千克所用时间与B型机器人搬运800千克所用时间相等.设B型机器人每小时搬运化工原料x千克,根据题意可列方程为(
)
A.
B.
C.
D.
15.某煤矿原计划x天生存120
t煤,由于采用新的技术,每天增加生存3
t,因此提前2天完成,列出的方程为(
)
A.
,
B.
C.
D.
二、填空题
1.若关于x的分式方程的解为正数,则满足条件的非负整数k的值为____.
2.已知关于x的分式方程有一个正数解,则k的取值范围为________.
3.若关于若关于x的分式方程的解为正数,那么字母a的取值范围是___.
4.已知关于的方程的解是正数,则的取值范围为__________.
三、解方程
1.解方程:(1).(2)
(3)
(4)+=1.
(5)
(6)=1+.
(7).
(8).
(9).
四、解答题
1.节能又环保的油电混合动力汽车,既可以用油做动力行驶,也可以用电做动力行驶,某品牌油电混合动力汽车从甲地行驶到乙地,若完全用油做动力行驶,则费用为80元;若完全用电做动力行驶,则费用为30元,已知汽车行驶中每千米用油费用比用电费用多0.5元.
(1)求:汽车行驶中每千米用电费用是多少元?甲、乙两地的距离是多少千米?
2.枇杷肉质厚实,鲜甜微酸,营养价值很高,是初夏里受人们喜爱的水果之一.枇杷一上市,某水果店的老板就用1350元购进一批枇杷,很快售完.老板又用1900元购进第二批枇杷,所购箱数是第一批的倍,但进价比第一批每箱多了5元.
(1)求第一批枇杷的每箱进价.
(2)老板以每箱145元的价格销售第二批枇杷,售出80%后,为了尽快售完,决定将剩下的打折促销.要使得第二批枇杷的销售利润不少于855元,剩余的枇杷每箱售价至多打几折?
3.荔枝是某地的特色时令水果.荔枝一上市,水果店的老板用2400元购进一批荔枝,很快售完:老板又用3700元购进第二批荔枝,所购件数是第一批的倍,但进价比第一批每件多了5元.
(1)第一批荔枝每件进价是多少元?
(2)老板以每件225元的价格销售第二批荔枝,售出80%后,为了尽快售完,剩下的决定打折促销.要使得第二批荔枝的销售利润不少于530元,剩余的荔枝每件售价至少打几折?
答案
一、选择题
1.D.2.C.3.B.4.D.5.C.6.C.7.A.8.C.
9.B.10.B.11.C.12.B.13.B.14.A.15.D.
二、填空题
1.0.
2.k<6且k≠3
3.a>1且a≠2
4.且
三、计算题
1.(1)去分母得:x(x+1)﹣x2+1=2,
去括号得:x2+x﹣x2+1=2,
解得:x=1,
经检验x=1是增根,分式方程无解.
(2)解:方程两边同时乘以(x-2),得:,
解得:,
检验:当时,,
所以是方程的增根,原方程无解;
(3)解:原方程即为:,
方程两边同时乘以,得:,
解得:,
检验:当时,,
是原方程的解.
(4)方程整理得:+=1,
去分母得:9x﹣7+4x﹣5=3x﹣2,
解得:x=1,
经检验x=1是分式方程的解.
(5)方程两边都乘以x(x-1)得3x-(x-2)=0
解这个方程得x=-1
当x=-1时x(x-1)≠0,
:.x=-1是原分式方程的解,.
(6)去分母得:2x=x﹣2﹣1,
解得:x=﹣3,
经检验x=﹣3是分式方程的解.
(7)去分母得:15x-12=4x+10-3x+6,
移项合并得:14x=28,
解得:x=2,
经检验x=2是增根,分式方程无解.
(8)解:,
,
1+2(x﹣2)=﹣x,
1+2x﹣4=﹣x,
2x+x=4﹣1,
3x=3,
x=1,
经检验,x=1是原方程的根.
(9)2(x-1)+(x+2)(x-1)=x(x+2)
x=4
检验:x=4是原方程的解
所以方程的解是x=4.
四、解答题
1.解:(1)设汽车行驶中每千米用电费用是x元,则每千米用油费用为(x+0.5)元,
可得:,
解得:x=0.3,
经检验x=0.3是原方程的解,
∴汽车行驶中每千米用电费用是0.3元,甲、乙两地的距离是30÷0.3=100千米;至少需要用电行驶60千米.
(2)汽车行驶中每千米用油费用为0.3+0.5=0.8元,
设汽车用电行驶ykm,
可得:0.3y+0.8(100-y)≤50,
解得:y≥60,
所以至少需要用电行驶60千米.
2.解:(1)设第一批枇杷每箱进价x元.
由题意得,
解得.
经检验,是原方程的根,且符合题意.
答:第一批枇杷每箱进价为90元.
(2)第二批购进枇杷的箱数为
设剩余的枇杷每箱售价打y折.
由题意可知,,
解得.
答:剩余的枇杷每箱售价至多打七五折.
3.解:(1)设第一批荔枝每件进价x元,则,
解得
x=180,
经检验,x=180是原方程的根,
答:第一批荔枝每件进价为180元;
(2)设剩余的荔枝每件售价打y折,
由题意知:
解得
y≥7,
答:剩余的荔枝每件售价至少打7折.
一、选择题
1.将方程去分母化简后,得到的方程是(
)
A.x﹣4=3﹣2
B.x﹣4=3﹣2x+1
C.x﹣4=3﹣2x+2
D.x﹣4=3﹣2x﹣2
2.方程=的解为(
)
A.x=3
B.x=4
C.x=5
D.x=﹣5
3.把分式方程
+
2
=化为整式方程,得( )
A.x+2=2x(x+2)
B.x+2(x2﹣4)=2x(x+2)
C.x+2(x﹣2)=2x(x﹣2)
D.x+2(x2﹣4)=2x(x﹣2)
4.解分式方程,分以下四步,其中错误的一步是(
)
A.方程两边各分式的最简公分母是
B.方程两边都乘以,得整式方程:
C.解这个整式方程,得
D.原方程的解为
5.若数
a使关于
x的分式方程有整数解,且关于y
的不等式组恰
好有两个奇数解,则符合条件的所有整数
a的和是(
)
A.7
B.5
C.2
D.1
6.若整数使得关于的方程的解为非负整数,且关于的不等式组至少有2个整数解,则所有符合条件的整数的和为(
)
A.6
B.9
C.13
D.16
7.关于的分式方程解为,则常数的值为(
).
A.
B.
C.
D.
8.已知关于x的分式方程+=1的解是非负数,则m的取值范围是(
)
A.m>2
B.m≥2
C.m≥2且m≠3
D.m>2且m≠3
9.为了帮助遭受自然灾害的地区重建家园,某学校号召同学们自愿捐款.已知第一次捐款总额为4
800元,第二次捐款总额为5
000元,第二次捐款人数比第一次多20人,而且两次人均捐款额恰好相等.如果设第一次捐款人数为x人,那么x满足的方程是(
)
A.
B.
C.
D.
10.某电子元件厂准备生产4600个电子元件,甲车间独立生产了一半后,由于要尽快投入市场,乙车间也加入该电子元件的生产,若乙车间每天生产的电子元件是甲车间的1.3倍,结果用33天完成任务,问甲车间每天生产电子元件多少个?在这个问题中设甲车间每天生产电子元件x个,根据题意可得方程为
A.
B.
C.
D.
11.八年级学生去距学校10千米的博物馆参观,一部分学生骑自行车先走,过了20分钟后,其余学生乘汽车出发,结果他们同时到达,已知汽车的速度是骑车学生速度的2倍.设骑车学生的速度为x千米/小时,则所列方程正确的是( )
A.-=20
B.-=20
C.-=
D.=
12.某口罩生产企业最近要紧急完成1000万只口罩生产的任务,在生产完400万只口罩后,新的生产线安装完毕,可以加入生产了;新的生产线加入后,每天口罩的生产总量比原来增加了,结果共用了8天完成了任务设新生产线加入前,每天生产口罩万只,则根据题意可得方程为(
)
A.
B.
C.
D.
13.现代互联网技术的广泛应用,催生了快递行业的高速发展.据调查,湘潭某家小型快递公司的分拣工小李和小江,在分拣同一类物件时,小李分拣120个物件所用的时间与小江分拣90个物件所用的时间相同,已知小李每小时比小江多分拣20个物件.若设小江每小时分拣个物件,则可列方程为( )
A.
B.
C.
D.
14.A,B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运40千克,A型机器人搬运1200千克所用时间与B型机器人搬运800千克所用时间相等.设B型机器人每小时搬运化工原料x千克,根据题意可列方程为(
)
A.
B.
C.
D.
15.某煤矿原计划x天生存120
t煤,由于采用新的技术,每天增加生存3
t,因此提前2天完成,列出的方程为(
)
A.
,
B.
C.
D.
二、填空题
1.若关于x的分式方程的解为正数,则满足条件的非负整数k的值为____.
2.已知关于x的分式方程有一个正数解,则k的取值范围为________.
3.若关于若关于x的分式方程的解为正数,那么字母a的取值范围是___.
4.已知关于的方程的解是正数,则的取值范围为__________.
三、解方程
1.解方程:(1).(2)
(3)
(4)+=1.
(5)
(6)=1+.
(7).
(8).
(9).
四、解答题
1.节能又环保的油电混合动力汽车,既可以用油做动力行驶,也可以用电做动力行驶,某品牌油电混合动力汽车从甲地行驶到乙地,若完全用油做动力行驶,则费用为80元;若完全用电做动力行驶,则费用为30元,已知汽车行驶中每千米用油费用比用电费用多0.5元.
(1)求:汽车行驶中每千米用电费用是多少元?甲、乙两地的距离是多少千米?
2.枇杷肉质厚实,鲜甜微酸,营养价值很高,是初夏里受人们喜爱的水果之一.枇杷一上市,某水果店的老板就用1350元购进一批枇杷,很快售完.老板又用1900元购进第二批枇杷,所购箱数是第一批的倍,但进价比第一批每箱多了5元.
(1)求第一批枇杷的每箱进价.
(2)老板以每箱145元的价格销售第二批枇杷,售出80%后,为了尽快售完,决定将剩下的打折促销.要使得第二批枇杷的销售利润不少于855元,剩余的枇杷每箱售价至多打几折?
3.荔枝是某地的特色时令水果.荔枝一上市,水果店的老板用2400元购进一批荔枝,很快售完:老板又用3700元购进第二批荔枝,所购件数是第一批的倍,但进价比第一批每件多了5元.
(1)第一批荔枝每件进价是多少元?
(2)老板以每件225元的价格销售第二批荔枝,售出80%后,为了尽快售完,剩下的决定打折促销.要使得第二批荔枝的销售利润不少于530元,剩余的荔枝每件售价至少打几折?
答案
一、选择题
1.D.2.C.3.B.4.D.5.C.6.C.7.A.8.C.
9.B.10.B.11.C.12.B.13.B.14.A.15.D.
二、填空题
1.0.
2.k<6且k≠3
3.a>1且a≠2
4.且
三、计算题
1.(1)去分母得:x(x+1)﹣x2+1=2,
去括号得:x2+x﹣x2+1=2,
解得:x=1,
经检验x=1是增根,分式方程无解.
(2)解:方程两边同时乘以(x-2),得:,
解得:,
检验:当时,,
所以是方程的增根,原方程无解;
(3)解:原方程即为:,
方程两边同时乘以,得:,
解得:,
检验:当时,,
是原方程的解.
(4)方程整理得:+=1,
去分母得:9x﹣7+4x﹣5=3x﹣2,
解得:x=1,
经检验x=1是分式方程的解.
(5)方程两边都乘以x(x-1)得3x-(x-2)=0
解这个方程得x=-1
当x=-1时x(x-1)≠0,
:.x=-1是原分式方程的解,.
(6)去分母得:2x=x﹣2﹣1,
解得:x=﹣3,
经检验x=﹣3是分式方程的解.
(7)去分母得:15x-12=4x+10-3x+6,
移项合并得:14x=28,
解得:x=2,
经检验x=2是增根,分式方程无解.
(8)解:,
,
1+2(x﹣2)=﹣x,
1+2x﹣4=﹣x,
2x+x=4﹣1,
3x=3,
x=1,
经检验,x=1是原方程的根.
(9)2(x-1)+(x+2)(x-1)=x(x+2)
x=4
检验:x=4是原方程的解
所以方程的解是x=4.
四、解答题
1.解:(1)设汽车行驶中每千米用电费用是x元,则每千米用油费用为(x+0.5)元,
可得:,
解得:x=0.3,
经检验x=0.3是原方程的解,
∴汽车行驶中每千米用电费用是0.3元,甲、乙两地的距离是30÷0.3=100千米;至少需要用电行驶60千米.
(2)汽车行驶中每千米用油费用为0.3+0.5=0.8元,
设汽车用电行驶ykm,
可得:0.3y+0.8(100-y)≤50,
解得:y≥60,
所以至少需要用电行驶60千米.
2.解:(1)设第一批枇杷每箱进价x元.
由题意得,
解得.
经检验,是原方程的根,且符合题意.
答:第一批枇杷每箱进价为90元.
(2)第二批购进枇杷的箱数为
设剩余的枇杷每箱售价打y折.
由题意可知,,
解得.
答:剩余的枇杷每箱售价至多打七五折.
3.解:(1)设第一批荔枝每件进价x元,则,
解得
x=180,
经检验,x=180是原方程的根,
答:第一批荔枝每件进价为180元;
(2)设剩余的荔枝每件售价打y折,
由题意知:
解得
y≥7,
答:剩余的荔枝每件售价至少打7折.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
