2021-2022学年人教版八年级数学上册11.1.3三角形的稳定性教学课件(共18张PPT)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册11.1.3三角形的稳定性教学课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-12 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
第十一章
三角形
11.1
与三角形有关的线段
11.1.3三角形的稳定性
目
录
CONTENTS
1
学习目标
2
新课导入
3
新课讲解
4
课堂小结
5
当堂小练
6
拓展与延伸
7
布置作业
1.了解三角形的稳定性.(重点)
2.了解三角形的稳定性和四边形不稳定性的应用.(难点)
学习目标
新课导入
情境导入
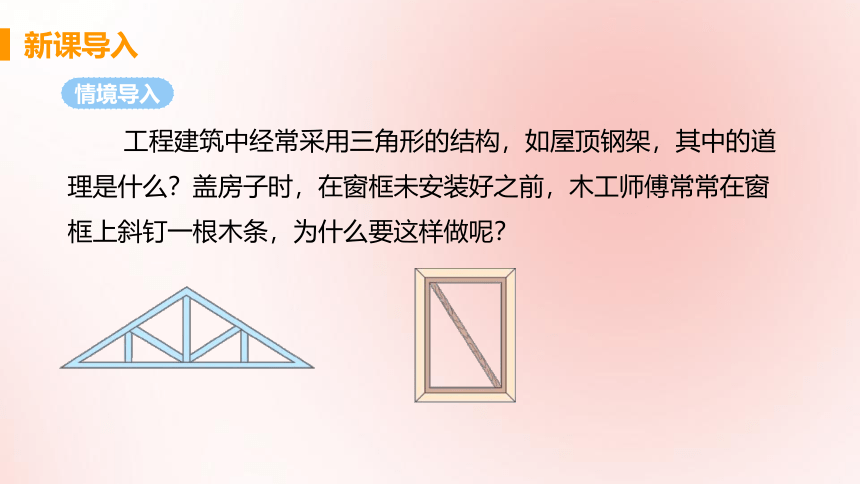
工程建筑中经常采用三角形的结构,如屋顶钢架,其中的道理是什么?盖房子时,在窗框未安装好之前,木工师傅常常在窗框上斜钉一根木条,为什么要这样做呢?
新课讲解
知识点1
三角形的稳定性
合作探究
探究1:如图,将三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?
分析:
不会改变,也就是说,三角形的三条边长确定后,三角形的形状就确定了.
新课讲解
知识点1
三角形的稳定性
合作探究
探究2:如图,将四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗?
分析:
会改变,也就是说,四边形的四条边长确定后,不能确定它的形状,它的各个角的大小可以改变.
新课讲解
知识点1
三角形的稳定性
合作探究
探究3:如图,四边形木架上再钉一根木条,将它的一对不相等的顶点连接起来,然后再扭动它,这时木架的形状会改变吗?为什么?
分析:
不会改变,三角形具有稳定性,四边形不具有稳定性.
新课讲解
“只要三角形三条边的长度固定,这个三角形的形状和大小也就完全确定,三角形的这种性质叫做“三角形的稳定性”.
这就是说,三角形的稳定性不是“拉得动、拉不动”的问题,其实质应是“三角形边长确定,其形状和大小就确定了”
结论
新课讲解
例
典例分析
1
小明用7根木条钉成一个七边形的木架,他为了使该木架稳固,
想在其中加上四根木条,请你在下图的三个图中画出你的三种想法.
解:如图所示(答案不唯一).
新课讲解
练一练
1.在如图
11-1-17
所示图形中,具有稳定性的有
.(只填序号)
①④⑥
1
分析:三角形具有稳定性,多边形不具有稳定性。如果图形可以继续切
割为三角形,则不具有稳定性
.
新课讲解
练一练
如图,工人师傅砌门时,常用木条EF固定门框ABCD,使其不变形,这种做法的根据是(
)
D
2
A.两点之间线段最短
B.三角形两边之和大于第三边
C.长方形的四个角都是直角
D.三角形的稳定性
新课讲解
练一练
下列图形中,不是应用三角形的稳定性的是(
)
C
3
A.房屋顶支撑架
B.自行车三脚架
C.伸缩门
D.木门上钉一条木条
新课讲解
练一练
3
4
如图,两条木条钉成一个六边形框架ABCD,要使框架稳固不活动,至少还需要添加()根木条.
解:答案不唯一,如图
课堂小结
稳定性
应用
三角形具有稳定性
四边形不具有稳定性
应用
当堂小练
(1)有下列图形:①正方形;②长方形;③直角三角形;④平行四边形.其中具有稳定性的是________.(填序号)
(2)铁栅门和多功能挂衣架能够伸缩自如,是利用四边形的______.
(3)要使五边形木架(用5根木条钉成)不变形,至少要钉上_____根木条.
③
不稳定性
2
D
拓展与延伸
(1)要使四边形木架(用四根木条钉成)具有稳定性,至少要再钉上几根木条?
(2)要使五边形木架(用五根木条钉成)具有稳定性,至少要再钉上几根木条?
(3)要使六边形木架(用六根木条钉成)具有稳定性,至少要再钉上几根木条?
(4)要使n边形木架(用n根木条钉成)具有稳定性,至少要再钉上几根木条?
D
拓展与延伸
(1)至少再需要1根木条,使得变成2个三角形.
(2)至少再需要2根木条,使得变成3个三角形.
(3)至少再需要3根木条,使得变成4个三角形.
D
拓展与延伸
(4)至少再需要(n-3)根木条,使得变成(n-2)个三角形.
根据四边形木架、五边形木架和六边形木架的规律,n边形木架至少再需要(n-3)根木条,使得变成(n-2)个三角形.
第十一章
三角形
11.1
与三角形有关的线段
11.1.3三角形的稳定性
目
录
CONTENTS
1
学习目标
2
新课导入
3
新课讲解
4
课堂小结
5
当堂小练
6
拓展与延伸
7
布置作业
1.了解三角形的稳定性.(重点)
2.了解三角形的稳定性和四边形不稳定性的应用.(难点)
学习目标
新课导入
情境导入
工程建筑中经常采用三角形的结构,如屋顶钢架,其中的道理是什么?盖房子时,在窗框未安装好之前,木工师傅常常在窗框上斜钉一根木条,为什么要这样做呢?
新课讲解
知识点1
三角形的稳定性
合作探究
探究1:如图,将三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?
分析:
不会改变,也就是说,三角形的三条边长确定后,三角形的形状就确定了.
新课讲解
知识点1
三角形的稳定性
合作探究
探究2:如图,将四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗?
分析:
会改变,也就是说,四边形的四条边长确定后,不能确定它的形状,它的各个角的大小可以改变.
新课讲解
知识点1
三角形的稳定性
合作探究
探究3:如图,四边形木架上再钉一根木条,将它的一对不相等的顶点连接起来,然后再扭动它,这时木架的形状会改变吗?为什么?
分析:
不会改变,三角形具有稳定性,四边形不具有稳定性.
新课讲解
“只要三角形三条边的长度固定,这个三角形的形状和大小也就完全确定,三角形的这种性质叫做“三角形的稳定性”.
这就是说,三角形的稳定性不是“拉得动、拉不动”的问题,其实质应是“三角形边长确定,其形状和大小就确定了”
结论
新课讲解
例
典例分析
1
小明用7根木条钉成一个七边形的木架,他为了使该木架稳固,
想在其中加上四根木条,请你在下图的三个图中画出你的三种想法.
解:如图所示(答案不唯一).
新课讲解
练一练
1.在如图
11-1-17
所示图形中,具有稳定性的有
.(只填序号)
①④⑥
1
分析:三角形具有稳定性,多边形不具有稳定性。如果图形可以继续切
割为三角形,则不具有稳定性
.
新课讲解
练一练
如图,工人师傅砌门时,常用木条EF固定门框ABCD,使其不变形,这种做法的根据是(
)
D
2
A.两点之间线段最短
B.三角形两边之和大于第三边
C.长方形的四个角都是直角
D.三角形的稳定性
新课讲解
练一练
下列图形中,不是应用三角形的稳定性的是(
)
C
3
A.房屋顶支撑架
B.自行车三脚架
C.伸缩门
D.木门上钉一条木条
新课讲解
练一练
3
4
如图,两条木条钉成一个六边形框架ABCD,要使框架稳固不活动,至少还需要添加()根木条.
解:答案不唯一,如图
课堂小结
稳定性
应用
三角形具有稳定性
四边形不具有稳定性
应用
当堂小练
(1)有下列图形:①正方形;②长方形;③直角三角形;④平行四边形.其中具有稳定性的是________.(填序号)
(2)铁栅门和多功能挂衣架能够伸缩自如,是利用四边形的______.
(3)要使五边形木架(用5根木条钉成)不变形,至少要钉上_____根木条.
③
不稳定性
2
D
拓展与延伸
(1)要使四边形木架(用四根木条钉成)具有稳定性,至少要再钉上几根木条?
(2)要使五边形木架(用五根木条钉成)具有稳定性,至少要再钉上几根木条?
(3)要使六边形木架(用六根木条钉成)具有稳定性,至少要再钉上几根木条?
(4)要使n边形木架(用n根木条钉成)具有稳定性,至少要再钉上几根木条?
D
拓展与延伸
(1)至少再需要1根木条,使得变成2个三角形.
(2)至少再需要2根木条,使得变成3个三角形.
(3)至少再需要3根木条,使得变成4个三角形.
D
拓展与延伸
(4)至少再需要(n-3)根木条,使得变成(n-2)个三角形.
根据四边形木架、五边形木架和六边形木架的规律,n边形木架至少再需要(n-3)根木条,使得变成(n-2)个三角形.
