2021-2022学年人教版九年级数学上册 21.2.4一元二次方程的根与系数的关系课件(共18张)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册 21.2.4一元二次方程的根与系数的关系课件(共18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 765.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 22:52:05 | ||
图片预览





文档简介
(共18张PPT)
21.2.4
一元二次方程的根与系数的关系
一元二次方程
ax2+bx+c=0(a≠0)
的求根公式:
x=
(b2-4ac≥
0)
算一算
(1)x2-7x+12=0
(2)x2+3x-4=0
(3)
2x2+3x-2=0
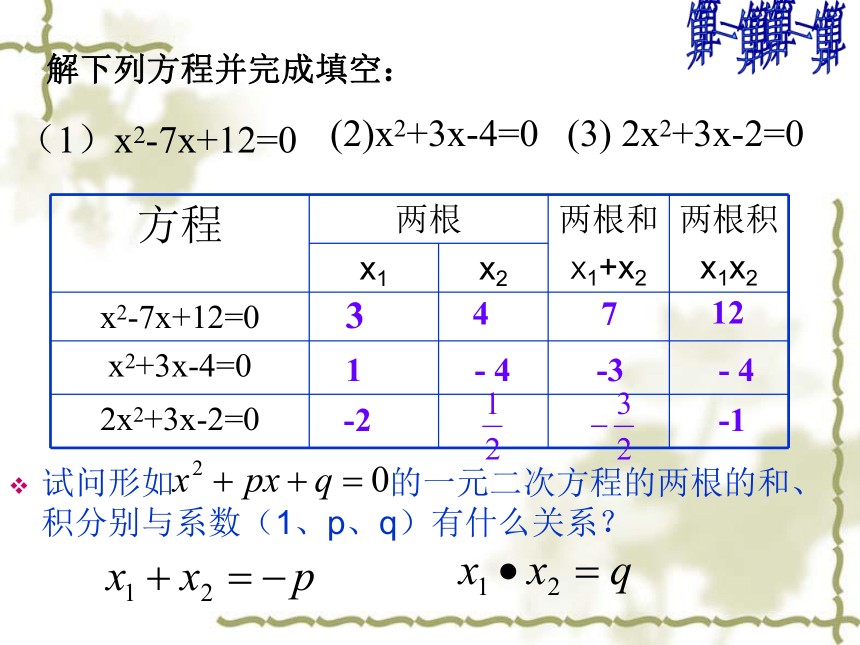
解下列方程并完成填空:
方程
两根
两根和
X1+x2
两根积
x1x2
x1
x2
x2-7x+12=0
x2+3x-4=0
2x2+3x-2=0
3
4
12
7
1
-3
-
4
-
4
-1
-2
试问形如
的一元二次方程的两根的和、积分别与系数(1、p、q)有什么关系?
方程
ax2+bx+c=0(a≠0)
两根
两根和
X1+x2
两根积
x1x2
x1
x2
3x2-4x-4=0
2x2-3x+1=0
6x2+7x-3=0
2
1
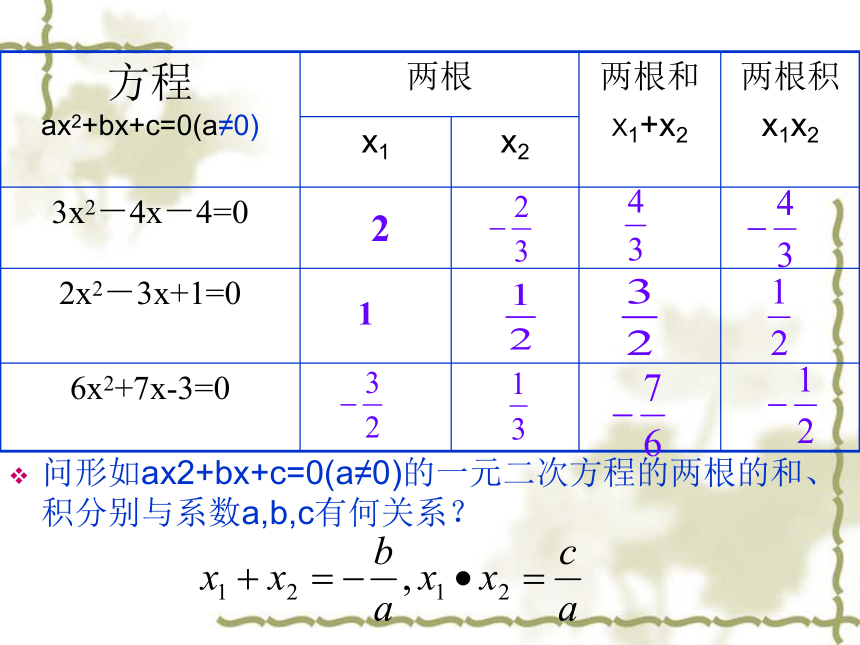
问形如ax2+bx+c=0(a≠0)的一元二次方程的两根的和、积分别与系数a,b,c有何关系?
推理验证:
(1)从因式分解法可知:方程(x-x1)(x-x2)=0
(x1,x2为已知数)的两根为x1和x2,将方程
x2+px+q=0的形式:x2-(x1+x2)x+x1x2=0
∴-(x1+x2)=p
x1x2=q
即
x1+x2=-p
x1x2=q
(2)ax2+bx+c=0(a≠0)的两根x1、x2与a,b,c的关系:设ax2+bx+c=0(a≠0)的两根为x1和x2
则
一元二次方程根与系数关系的证明:
X1+x2=
+
=
=
X1x2=
●
=
=
=
∴任何一个一元二次方程的根与系数的关系为:
两个根的和等于一次项系数与二次项系数的比的相反数。
两个根的积等于常数项与二次项系数的比。
即:
注:能用根与系数的关系的前提条件为b2-4ac≥0
例 根据一元二次方程的根与系数的关系,求下列方程两个根
x1,x2
的和与积:
(1)
x
2
-
6x
-
15
=
0
(2)3x
2
+
7x
-
9
=
0
(3)5x
-
1
=
4x
2
运用性质,巩固练习
x1
+
x2
=
6
x1
x2
=
-15
x1
+
x2
=
x1
x2
=
-3
x1
+
x2
=
x1
x2
=
方程化为
课堂巩固练习:课本P16
练习
布置作业:课本P17
第7题
∴
答:方程的另一个根是
,
的值是
。
例、已知方程
求它的另一个根及
的一个根是2
的值。
想一想,还有其他方法吗?
还可以把
代入方程的两边,求出
解:
,那么
设方程的另一根是
∴
又∵
我能行
例、不解方程,求一元二次方程
两个根的①平方和;②倒数和。
设方程的两根是
,那么
①
②
解:
我能行
所求的方程是:
解:
我能行
例、求运用根与系数的关系一个一元二次方程,使它的两个根是:
,
即:
或:
(1)下列方程两根的和与两根的积各是多少?
;②
③
;④
①
求它的另一个根及
(2)已知方程
的值。
的一个根是1,
是方程
不解方程,求下列各式的值:
(3)设
的两个根,
①
②
开启
智慧
知识在于积累
开启
智慧
知识在于积累
(4)求一个一元二次方程,使它的两个根分别为:
;②
①
(5)已知两个数的和等于
,积等于
求这两个数
拓广探索
1、当k为何值时,方程2x2-(k+1)x+k+3=0的两根差为1。
解:设方程两根分别为x1,x2(x1>x2),则x1-x2=1
∵
(x2-x1)2=(x1+x2)2-4x1x2
∴
解得k1=9,k2=
-3
当k=9或-3时,由于△≥0,∴k的值为9或-3。
由根与系数的关系得:x1+x2=
x1x2=
2、设x1,x2是方程x2-2(k-1)x+k2=0的两个实数根,且x12+x22=4,求k的值。
拓广探索
解:由方程有两个实数根,得
即-8k+4≥0
由根与系数的关系得x1+x2=
2(k-1)
,
x1x2=k2
∴
X12+x22=(x1+x2)2-2x1x2=4(k-1)2-2k2=2k2-8k+4
由X12+x22
=4,得2k2-8k+4=4
解得k1=0
,
k2=4
经检验,
k2=4不合题意,舍去。
∴
k=0
提升能力:
1、小华与小丽在一起做作业时,小华看错了一元二次方程的一次项系数,解得X1=2
X2=3;小丽看错同一个方程的常数项,解得X1=-6
X2=3,若二次项系数为1,则原方程为
。
2、当m为何值时,关于x的一元二次方程x2-(5m2+4m-1)x+m=0的两根互为相反数?
3、已知整数系数方程x2+(m+3)x+2m+3=0有一个正根和一个负根,且正根的绝对值较小,求m的值和方程的根。
4、已知关于的方程x2-2(m-2)x+m2=0,试问:是否存在实数m,使得方程的两个实数根的平方和等于56。若存在,求出m的值;若不存在,试说明理由。
5、小王同学自编一道题:
设k=3,方程x2-3x+k=0的两个实数根是x1、x2,求
的值。
解:∵k=3
∴方程为x2-3x+3=0,又∵
x1+x2=3,
x1x2=3
(1)请你对小王同学解答作出评价,并简述理由。
(2)请你对小王同学所编的练习题中的k另取一个适当的整数,其他条件不变,求
的值
6、已知方程2x2+kx-2k+1=0的两实数根的平方和是
,求k的值
∴
21.2.4
一元二次方程的根与系数的关系
一元二次方程
ax2+bx+c=0(a≠0)
的求根公式:
x=
(b2-4ac≥
0)
算一算
(1)x2-7x+12=0
(2)x2+3x-4=0
(3)
2x2+3x-2=0
解下列方程并完成填空:
方程
两根
两根和
X1+x2
两根积
x1x2
x1
x2
x2-7x+12=0
x2+3x-4=0
2x2+3x-2=0
3
4
12
7
1
-3
-
4
-
4
-1
-2
试问形如
的一元二次方程的两根的和、积分别与系数(1、p、q)有什么关系?
方程
ax2+bx+c=0(a≠0)
两根
两根和
X1+x2
两根积
x1x2
x1
x2
3x2-4x-4=0
2x2-3x+1=0
6x2+7x-3=0
2
1
问形如ax2+bx+c=0(a≠0)的一元二次方程的两根的和、积分别与系数a,b,c有何关系?
推理验证:
(1)从因式分解法可知:方程(x-x1)(x-x2)=0
(x1,x2为已知数)的两根为x1和x2,将方程
x2+px+q=0的形式:x2-(x1+x2)x+x1x2=0
∴-(x1+x2)=p
x1x2=q
即
x1+x2=-p
x1x2=q
(2)ax2+bx+c=0(a≠0)的两根x1、x2与a,b,c的关系:设ax2+bx+c=0(a≠0)的两根为x1和x2
则
一元二次方程根与系数关系的证明:
X1+x2=
+
=
=
X1x2=
●
=
=
=
∴任何一个一元二次方程的根与系数的关系为:
两个根的和等于一次项系数与二次项系数的比的相反数。
两个根的积等于常数项与二次项系数的比。
即:
注:能用根与系数的关系的前提条件为b2-4ac≥0
例 根据一元二次方程的根与系数的关系,求下列方程两个根
x1,x2
的和与积:
(1)
x
2
-
6x
-
15
=
0
(2)3x
2
+
7x
-
9
=
0
(3)5x
-
1
=
4x
2
运用性质,巩固练习
x1
+
x2
=
6
x1
x2
=
-15
x1
+
x2
=
x1
x2
=
-3
x1
+
x2
=
x1
x2
=
方程化为
课堂巩固练习:课本P16
练习
布置作业:课本P17
第7题
∴
答:方程的另一个根是
,
的值是
。
例、已知方程
求它的另一个根及
的一个根是2
的值。
想一想,还有其他方法吗?
还可以把
代入方程的两边,求出
解:
,那么
设方程的另一根是
∴
又∵
我能行
例、不解方程,求一元二次方程
两个根的①平方和;②倒数和。
设方程的两根是
,那么
①
②
解:
我能行
所求的方程是:
解:
我能行
例、求运用根与系数的关系一个一元二次方程,使它的两个根是:
,
即:
或:
(1)下列方程两根的和与两根的积各是多少?
;②
③
;④
①
求它的另一个根及
(2)已知方程
的值。
的一个根是1,
是方程
不解方程,求下列各式的值:
(3)设
的两个根,
①
②
开启
智慧
知识在于积累
开启
智慧
知识在于积累
(4)求一个一元二次方程,使它的两个根分别为:
;②
①
(5)已知两个数的和等于
,积等于
求这两个数
拓广探索
1、当k为何值时,方程2x2-(k+1)x+k+3=0的两根差为1。
解:设方程两根分别为x1,x2(x1>x2),则x1-x2=1
∵
(x2-x1)2=(x1+x2)2-4x1x2
∴
解得k1=9,k2=
-3
当k=9或-3时,由于△≥0,∴k的值为9或-3。
由根与系数的关系得:x1+x2=
x1x2=
2、设x1,x2是方程x2-2(k-1)x+k2=0的两个实数根,且x12+x22=4,求k的值。
拓广探索
解:由方程有两个实数根,得
即-8k+4≥0
由根与系数的关系得x1+x2=
2(k-1)
,
x1x2=k2
∴
X12+x22=(x1+x2)2-2x1x2=4(k-1)2-2k2=2k2-8k+4
由X12+x22
=4,得2k2-8k+4=4
解得k1=0
,
k2=4
经检验,
k2=4不合题意,舍去。
∴
k=0
提升能力:
1、小华与小丽在一起做作业时,小华看错了一元二次方程的一次项系数,解得X1=2
X2=3;小丽看错同一个方程的常数项,解得X1=-6
X2=3,若二次项系数为1,则原方程为
。
2、当m为何值时,关于x的一元二次方程x2-(5m2+4m-1)x+m=0的两根互为相反数?
3、已知整数系数方程x2+(m+3)x+2m+3=0有一个正根和一个负根,且正根的绝对值较小,求m的值和方程的根。
4、已知关于的方程x2-2(m-2)x+m2=0,试问:是否存在实数m,使得方程的两个实数根的平方和等于56。若存在,求出m的值;若不存在,试说明理由。
5、小王同学自编一道题:
设k=3,方程x2-3x+k=0的两个实数根是x1、x2,求
的值。
解:∵k=3
∴方程为x2-3x+3=0,又∵
x1+x2=3,
x1x2=3
(1)请你对小王同学解答作出评价,并简述理由。
(2)请你对小王同学所编的练习题中的k另取一个适当的整数,其他条件不变,求
的值
6、已知方程2x2+kx-2k+1=0的两实数根的平方和是
,求k的值
∴
同课章节目录
