八年级数学下册试题 一课一练 1.2《直角三角形》习题-北师大版(word版含答案)
文档属性
| 名称 | 八年级数学下册试题 一课一练 1.2《直角三角形》习题-北师大版(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 405.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-12 00:00:00 | ||
图片预览




文档简介
1.2《直角三角形》习题
一、选择题
1.如图,在中,,,AD是的中线,AE是的角平分线,交AE的延长线于点F,则DF的长是
A.2
B.4
C.5
D.
2.如图,∠AOB=150°,OC平分∠AOB,P为OC上一点,PD∥OA交OB于点D,PE⊥OA于点E.若OD=4,则PE的长为( )
A.2
B.2.5
C.3
D.4
3.如图5,一棵大树在一次强台风中于离地面5米处折断倒下,倒下部分与地面成30°夹角,这棵大树在折断前的高度为(
)
A.10米
B.15米
C.25米
D.30米
4.某平原有一条很直的小河和两个村庄,要在此小河边的某处修建一个水泵站向这两个村庄供水.
某同学用直线(虛线)表示小河,两点表示村庄,线段(实线)表示铺设的管道,画出了如下四个示意图,则所需管道最短的是(
).
A.
B.
C.
D.
5.如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是
A.(0,0)
B.(0,1)
C.(0,2)
D.(0,3)
6.下列长度的三条线段能组成直角三角形的是(
)
A.2,
3,
4
B.4,6,7
C.3,4,
5
D.6,8,11
7.下列条件中,使不是直角三角形的是(
)
A.,,
B.
C.
D.
8.下列各组数中,以,,为边的三角形不是直角三角形的是(
)
A.,,
B.,,
C.,,
D.,,
9.以下列各组数为边长的三角形中,能组成直角三角形的是(
)
A.2,4,6
B.4,6,8
C.5,12,13
D.8,10,12
10.在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,下列条件不能判断△ABC是直角三角形的是( )
A.∠B=∠C+∠A
B.a2=(b+c)(b﹣c)
C.∠A:∠B:∠C=3:4:5
D.a:b:c=3:4:5
11.下列长度的各组线段中,不能构成直角三角形的是( )
A.4、5、6
B.5、12、13
C.3、4、5
D.1、、
12.由下列条件不能判定为直角三角形的是(
)
A.
B.
C.
D.,,
13.在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,下列说法错误的是(
)
A.如果∠C-∠B=∠A,则△ABC是直角三角形
B.如果c2=b2-a2,则△ABC是直角三角形
C.如果∠A:∠B:∠C=1:2:3,则△ABC是直角三角形
D.如果a2+b2≠c2,则△ABC不是直角三角形
二、填空题
1.如图,边长为12的等边三角形ABC中,E是高AD上的一个动点,连结CE,将线段CE绕点C逆时针旋转60°得到CF,连结DF.则在点E运动过程中,线段DF长度的最小值是__________.
2.如图,△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则在①3.6②4,③5.5,④7,这四个数中AP长不可能是_____
(填序号)
3.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=10,将△ABC沿CB方向向右平移得到△DEF.若四边形ABED的面积为20,则平移距离为___________.
4.如图,△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=6,则CD=_______.
5.如图,将一幅三角尺如图所示叠放在一起,若AB=24cm,则阴影部分的面积是_
_.
三、解答题
1.如图,,,,,.求该图形的面积.
2.如图,在△ABC中,已知AB=8,BC=12,AC=18,直线DE是线段AB的垂直平分线,已知线段DE=3.
(1)求CD的长;
(2)连接BD,△DBC为何种特殊三角形?并说明理由.
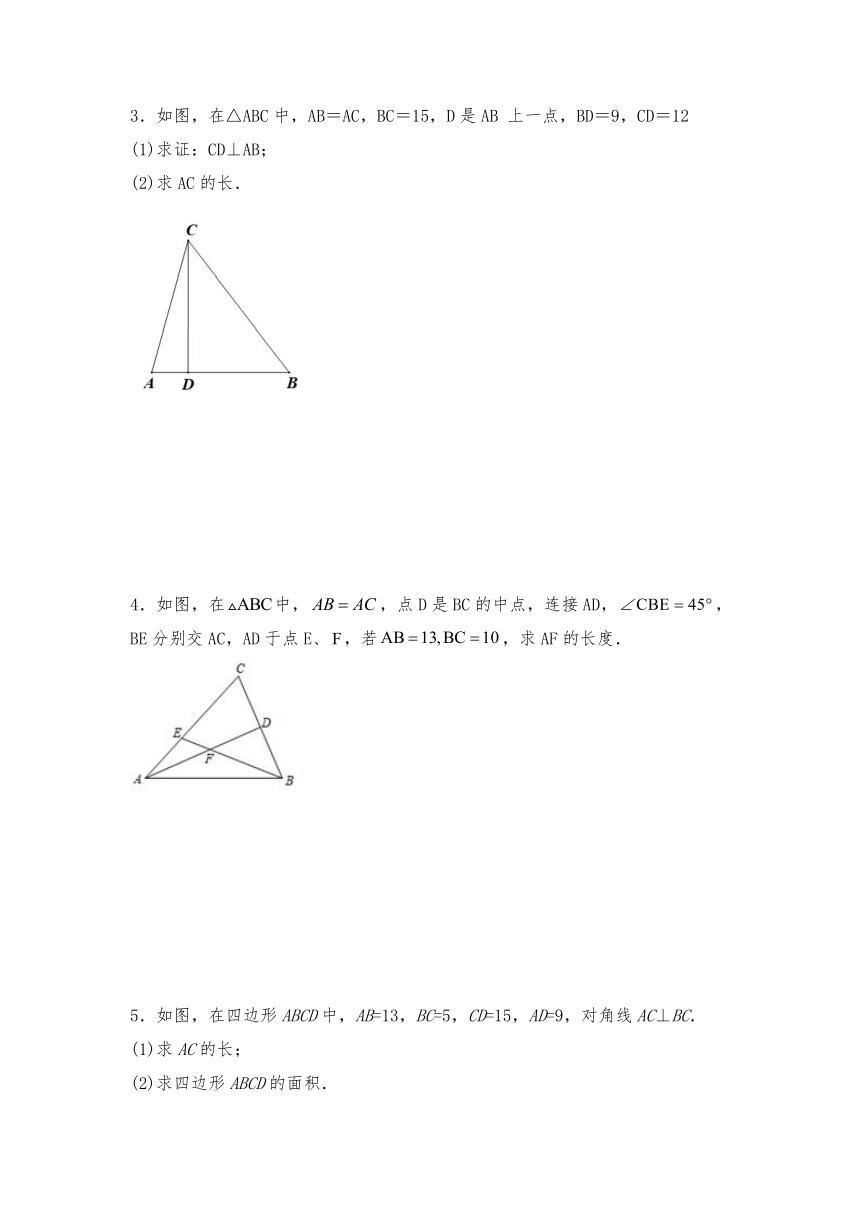
3.如图,在△ABC中,AB=AC,BC=15,D是AB
上一点,BD=9,CD=12
(1)求证:CD⊥AB;
(2)求AC的长.
4.如图,在中,,点D是BC的中点,连接AD,,BE分别交AC,AD于点E、,若,求AF的长度.
5.如图,在四边形ABCD中,AB=13,BC=5,CD=15,AD=9,对角线AC⊥BC.
(1)求AC的长;
(2)求四边形ABCD的面积.
6.如图,在四边形ABDC中,,,,,.
(1)连接BC,求BC的长;
(2)求的面积.
7.如图,已知四边形ABCD中,AB=24,AD=15,BC=20,CD=7,∠ADB+∠CBD=90°.
(1)在BD的上方作△A'BD,使△A'BD≌△ADB(点A与点不重合)(不写作法,保留作图痕迹);
(2)求四边形ABCD的面积.
8.如图,△ABC中,BC的垂直平分线DE分别交AB、BC于点D、E,且BD2﹣DA2=AC2.
(1)求证:∠A=90°;
(2)若AB=8,AD:BD=3:5,求AC的长.
9.在图中,A(1,3),B(﹣2,0)和C(2,﹣4)是一个直角三角形的顶点.
(1)求AB和BC的长度,答案以根式表示;
(2)求△ABC的面积.
10.如图,已知在中,,为边的中点,过点作,,垂足分别为,.
(1)求证:;
(2)若,,求的周长.
11.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,求OM的长.
答案
一、选择题
1.C.2.A.3.B.4.C.5.D.6.C.7.C.8.B.
9.C.10.C.11.A.12.B.13.D.
二、填空题
1.3
2.④
3.4
4.3.
5.72cm2.
三、解答题
1.解:连接.
∵在中,,,
∴.
在中,
∵,
∴为直角三角形.
∴该图形的面积为.
2.解:(1)∵DE是线段AB的垂直平分线,AB=8
∴AE=EB=4,∠AED=90°;
在直角△ADE中,AE=4,DE=3,
∴;
∵AC=18,
∴DC=AC-AD=13;
(2)△BCD是直角三角形.
理由如下:
∵DE是线段AB的垂直平分线,
∴DB=AD=5;
在△BCD中,BD=5,BC=12,CD=13.
∵
∴
∴△BCD是直角三角形
3.证明:(1)
(2)
设
则
4.解:,
,
,
,
中,,
,
中,,
是等腰直角三角形,
,
.
5.(1),
是直角三角形,
,
;
(2),
,
是直角三角形,
则四边形ABCD的面积为,
,
,
即四边形ABCD的面积为84.
6.(1)∵在中,,,,
∴;
(2)∵,,,
∴,
即,
∴是直角三角形,且,
∴的面积为.
7.
解:(1)如图1所示,△A′BD即为所求;
(2)由(1)中作图得知:∠A′BD=∠ADB,A′B=AD=15,A′D=AB=24,连接A′C,如图2,
∵∠ADB+∠CBD=90°,
∴∠A′BD+∠CBD=90°,
即∠A′BC=90°,
∴A′B2+BC2=A′C2,
∵A′B=15,BC=20,
∴A′C=25,
在△A′CD中,A′D=24,CD=7,
∴A′D2+CD2=576+49=625,
∵A′C2=625,
∴A′D2+CD2=A′C2.
∴△A′DC是直角三角形,且∠A′DC=90°,
∴S四边形A′BCD=S△A′BC+S△A′CD
∵S△A'BD=S△ABD,
∴S四边形ABCD=S四边形A'BCD=234.
8.
(1)证明:连接CD,
∵BC的垂直平分线DE分别交AB、BC于点D、E,
∴CD=DB,
∵BD2﹣DA2=AC2,
∴CD2﹣DA2=AC2,
∴CD2=AD2+AC2,
∴△ACD是直角三角形,且∠A=90°;
(2)解:∵AB=8,AD:BD=3:5,
∴AD=3,BD=5,
∴CD=BD=5,
∴在中,.
9.(1)AB=,
BC=;
(2)∵
AC=,
且AB2+BC2=AC2,
∴△ABC为直角三角形,且∠ABC=90°,
则△ABC的面积为.
10.(1)证明:
∵DE⊥AB,DF⊥A,
∴∠BED=∠CFD=90°,
∵AB=AC,
∴∠C=∠B,
∵D是BC的中点,
∴.BD=CD,
在△BED和△CFD中,
,
∴△BED≌△CFD,
∴DE=DF
;?
???
(2)解:∵AB=AC,
∠A=60°,
∴△ABC为等边三角形,
.∴∠B=60°,
∵∠BED=90°,
∴∠BDE=30°,
∴,
∵BE=1,
∴BD=2,
∴BC=2BD=4.
?∴△ABC的周长为12.
11.解:过P作PD⊥OB,交OB于点D,
在Rt△OPD中,∠AOB=60?,OP=12,∴OD=OP=6,
∵PM=PN,PD⊥MN,MN=2,
∴MD=ND=MN=1,
∴OM=OD-MD=6-1=5.
一、选择题
1.如图,在中,,,AD是的中线,AE是的角平分线,交AE的延长线于点F,则DF的长是
A.2
B.4
C.5
D.
2.如图,∠AOB=150°,OC平分∠AOB,P为OC上一点,PD∥OA交OB于点D,PE⊥OA于点E.若OD=4,则PE的长为( )
A.2
B.2.5
C.3
D.4
3.如图5,一棵大树在一次强台风中于离地面5米处折断倒下,倒下部分与地面成30°夹角,这棵大树在折断前的高度为(
)
A.10米
B.15米
C.25米
D.30米
4.某平原有一条很直的小河和两个村庄,要在此小河边的某处修建一个水泵站向这两个村庄供水.
某同学用直线(虛线)表示小河,两点表示村庄,线段(实线)表示铺设的管道,画出了如下四个示意图,则所需管道最短的是(
).
A.
B.
C.
D.
5.如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是
A.(0,0)
B.(0,1)
C.(0,2)
D.(0,3)
6.下列长度的三条线段能组成直角三角形的是(
)
A.2,
3,
4
B.4,6,7
C.3,4,
5
D.6,8,11
7.下列条件中,使不是直角三角形的是(
)
A.,,
B.
C.
D.
8.下列各组数中,以,,为边的三角形不是直角三角形的是(
)
A.,,
B.,,
C.,,
D.,,
9.以下列各组数为边长的三角形中,能组成直角三角形的是(
)
A.2,4,6
B.4,6,8
C.5,12,13
D.8,10,12
10.在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,下列条件不能判断△ABC是直角三角形的是( )
A.∠B=∠C+∠A
B.a2=(b+c)(b﹣c)
C.∠A:∠B:∠C=3:4:5
D.a:b:c=3:4:5
11.下列长度的各组线段中,不能构成直角三角形的是( )
A.4、5、6
B.5、12、13
C.3、4、5
D.1、、
12.由下列条件不能判定为直角三角形的是(
)
A.
B.
C.
D.,,
13.在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,下列说法错误的是(
)
A.如果∠C-∠B=∠A,则△ABC是直角三角形
B.如果c2=b2-a2,则△ABC是直角三角形
C.如果∠A:∠B:∠C=1:2:3,则△ABC是直角三角形
D.如果a2+b2≠c2,则△ABC不是直角三角形
二、填空题
1.如图,边长为12的等边三角形ABC中,E是高AD上的一个动点,连结CE,将线段CE绕点C逆时针旋转60°得到CF,连结DF.则在点E运动过程中,线段DF长度的最小值是__________.
2.如图,△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则在①3.6②4,③5.5,④7,这四个数中AP长不可能是_____
(填序号)
3.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=10,将△ABC沿CB方向向右平移得到△DEF.若四边形ABED的面积为20,则平移距离为___________.
4.如图,△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=6,则CD=_______.
5.如图,将一幅三角尺如图所示叠放在一起,若AB=24cm,则阴影部分的面积是_
_.
三、解答题
1.如图,,,,,.求该图形的面积.
2.如图,在△ABC中,已知AB=8,BC=12,AC=18,直线DE是线段AB的垂直平分线,已知线段DE=3.
(1)求CD的长;
(2)连接BD,△DBC为何种特殊三角形?并说明理由.
3.如图,在△ABC中,AB=AC,BC=15,D是AB
上一点,BD=9,CD=12
(1)求证:CD⊥AB;
(2)求AC的长.
4.如图,在中,,点D是BC的中点,连接AD,,BE分别交AC,AD于点E、,若,求AF的长度.
5.如图,在四边形ABCD中,AB=13,BC=5,CD=15,AD=9,对角线AC⊥BC.
(1)求AC的长;
(2)求四边形ABCD的面积.
6.如图,在四边形ABDC中,,,,,.
(1)连接BC,求BC的长;
(2)求的面积.
7.如图,已知四边形ABCD中,AB=24,AD=15,BC=20,CD=7,∠ADB+∠CBD=90°.
(1)在BD的上方作△A'BD,使△A'BD≌△ADB(点A与点不重合)(不写作法,保留作图痕迹);
(2)求四边形ABCD的面积.
8.如图,△ABC中,BC的垂直平分线DE分别交AB、BC于点D、E,且BD2﹣DA2=AC2.
(1)求证:∠A=90°;
(2)若AB=8,AD:BD=3:5,求AC的长.
9.在图中,A(1,3),B(﹣2,0)和C(2,﹣4)是一个直角三角形的顶点.
(1)求AB和BC的长度,答案以根式表示;
(2)求△ABC的面积.
10.如图,已知在中,,为边的中点,过点作,,垂足分别为,.
(1)求证:;
(2)若,,求的周长.
11.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,求OM的长.
答案
一、选择题
1.C.2.A.3.B.4.C.5.D.6.C.7.C.8.B.
9.C.10.C.11.A.12.B.13.D.
二、填空题
1.3
2.④
3.4
4.3.
5.72cm2.
三、解答题
1.解:连接.
∵在中,,,
∴.
在中,
∵,
∴为直角三角形.
∴该图形的面积为.
2.解:(1)∵DE是线段AB的垂直平分线,AB=8
∴AE=EB=4,∠AED=90°;
在直角△ADE中,AE=4,DE=3,
∴;
∵AC=18,
∴DC=AC-AD=13;
(2)△BCD是直角三角形.
理由如下:
∵DE是线段AB的垂直平分线,
∴DB=AD=5;
在△BCD中,BD=5,BC=12,CD=13.
∵
∴
∴△BCD是直角三角形
3.证明:(1)
(2)
设
则
4.解:,
,
,
,
中,,
,
中,,
是等腰直角三角形,
,
.
5.(1),
是直角三角形,
,
;
(2),
,
是直角三角形,
则四边形ABCD的面积为,
,
,
即四边形ABCD的面积为84.
6.(1)∵在中,,,,
∴;
(2)∵,,,
∴,
即,
∴是直角三角形,且,
∴的面积为.
7.
解:(1)如图1所示,△A′BD即为所求;
(2)由(1)中作图得知:∠A′BD=∠ADB,A′B=AD=15,A′D=AB=24,连接A′C,如图2,
∵∠ADB+∠CBD=90°,
∴∠A′BD+∠CBD=90°,
即∠A′BC=90°,
∴A′B2+BC2=A′C2,
∵A′B=15,BC=20,
∴A′C=25,
在△A′CD中,A′D=24,CD=7,
∴A′D2+CD2=576+49=625,
∵A′C2=625,
∴A′D2+CD2=A′C2.
∴△A′DC是直角三角形,且∠A′DC=90°,
∴S四边形A′BCD=S△A′BC+S△A′CD
∵S△A'BD=S△ABD,
∴S四边形ABCD=S四边形A'BCD=234.
8.
(1)证明:连接CD,
∵BC的垂直平分线DE分别交AB、BC于点D、E,
∴CD=DB,
∵BD2﹣DA2=AC2,
∴CD2﹣DA2=AC2,
∴CD2=AD2+AC2,
∴△ACD是直角三角形,且∠A=90°;
(2)解:∵AB=8,AD:BD=3:5,
∴AD=3,BD=5,
∴CD=BD=5,
∴在中,.
9.(1)AB=,
BC=;
(2)∵
AC=,
且AB2+BC2=AC2,
∴△ABC为直角三角形,且∠ABC=90°,
则△ABC的面积为.
10.(1)证明:
∵DE⊥AB,DF⊥A,
∴∠BED=∠CFD=90°,
∵AB=AC,
∴∠C=∠B,
∵D是BC的中点,
∴.BD=CD,
在△BED和△CFD中,
,
∴△BED≌△CFD,
∴DE=DF
;?
???
(2)解:∵AB=AC,
∠A=60°,
∴△ABC为等边三角形,
.∴∠B=60°,
∵∠BED=90°,
∴∠BDE=30°,
∴,
∵BE=1,
∴BD=2,
∴BC=2BD=4.
?∴△ABC的周长为12.
11.解:过P作PD⊥OB,交OB于点D,
在Rt△OPD中,∠AOB=60?,OP=12,∴OD=OP=6,
∵PM=PN,PD⊥MN,MN=2,
∴MD=ND=MN=1,
∴OM=OD-MD=6-1=5.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
