北师大版八年级数学下册一课一练试题 1.4《角平分线》(Word版 含答案)
文档属性
| 名称 | 北师大版八年级数学下册一课一练试题 1.4《角平分线》(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 347.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-12 13:11:40 | ||
图片预览



文档简介
1.4《角平分线》
一、选择题
1.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为( )
A.
B.
C.3
D.
2.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为用A、B.下列结论中不一定成立的是(
)
A.PA=PE
B.PO平分∠APB
C.AB垂直平分OP
D.OA=OB
3.如图,在中,,以顶点为圆心,适当长为半径画弧,分别交,于点,,再分别以点,为圆心,大于的长为半径画弧,两弧交于点,作射线交边于点,若,,则的面积是
(
)
A.15
B.30
C.45
D.60
4.如图,a、b、c三条公路的位置相交成三角形,现决定在三条公路之间建一购物超市,使超市到三条公路的距离相等,则超市应建在(
)
A.三角形两边高线的交点处
B.三角形两边中线的交点处
C.∠α的平分线上
D.∠α和∠β的平分线的交点处
5.如图,在中,,以点为圆心,适当长为半径画弧,分别交于点,再分别以点为圆心,大于为半径画弧,两弧交于点,作射线交边于点,则的面积是( )
A.
B.
C.
D.
6.如图所示,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=3cm,那么AE+DE等于(
)
A.2cm
B.3cm
C.4cm
D.5cm
7.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为( )
A.11
B.5.5
C.7
D.3.5
8.如图,在△ABC中,E为AC的中点,AD平分∠BAC,BA:CA=2:3,AD与BE相交于点O,若△OAE的面积比△BOD的面积大1,则△ABC的面积是( )
A.8
B.9
C.10
D.11
9.如图尺规作业,为的平分线,这样的作法依据是( )
A.
B.
C.
D.
10.如图,△ABC
中,点
E,F,G
分别在
BC,AC,AB
上,AE
与
BF
交于点
O,且点
O
在
CG
上,根据尺规作图的痕迹,判断下列说法不正确的是(
)
A.AE,BF
是△ABC
的角平分线
B.点
O
到△ABC
三边的距离相等
C.CG
也是△ABC
的一条角平分线
D.AO=BO=CO
11.如图,在中,尺规作图如下:在射线、上,分别截取、,使;分别以点和点为圆心、大于的长为半径作弧,两弧相交于点;作射线,连结、.下列结论不一定成立的是(
)
A.
B.
C.
D.
二、填空题
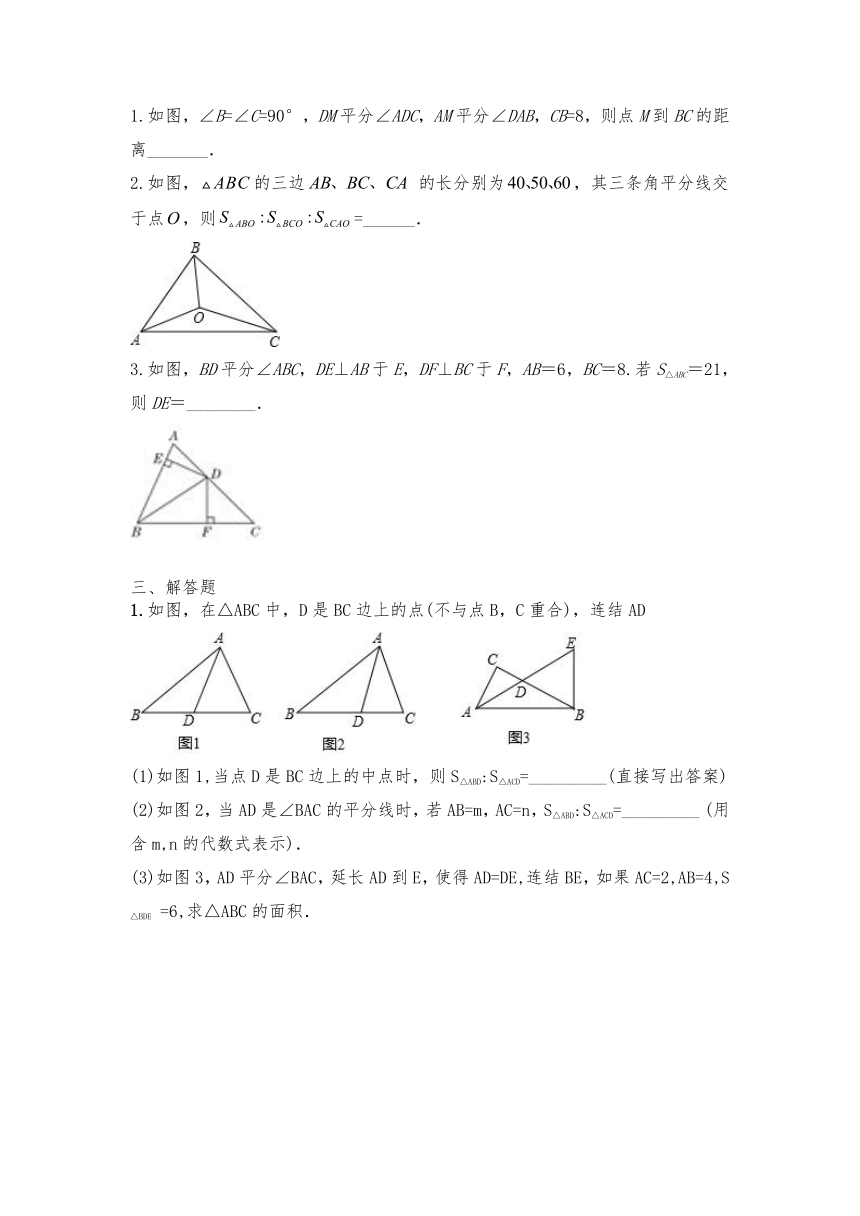
1.如图,∠B=∠C=90°,DM平分∠ADC,AM平分∠DAB,CB=8,则点M到BC的距离_______.
2.如图,的三边
的长分别为,其三条角平分线交于点,则=______.
3.如图,BD平分∠ABC,DE⊥AB于E,DF⊥BC于F,AB=6,BC=8.若S△ABC=21,则DE=________.
三、解答题
1.如图,在△ABC中,D是BC边上的点(不与点B,C重合),连结AD
(1)如图1,当点D是BC边上的中点时,则S△ABD:S△ACD=_________(直接写出答案)
(2)如图2,当AD是∠BAC的平分线时,若AB=m,AC=n,S△ABD:S△ACD=_________
(用含m,n的代数式表示).
(3)如图3,AD平分∠BAC,延长AD到E,使得AD=DE,连结BE,如果AC=2,AB=4,S△BDE
=6,求△ABC的面积.
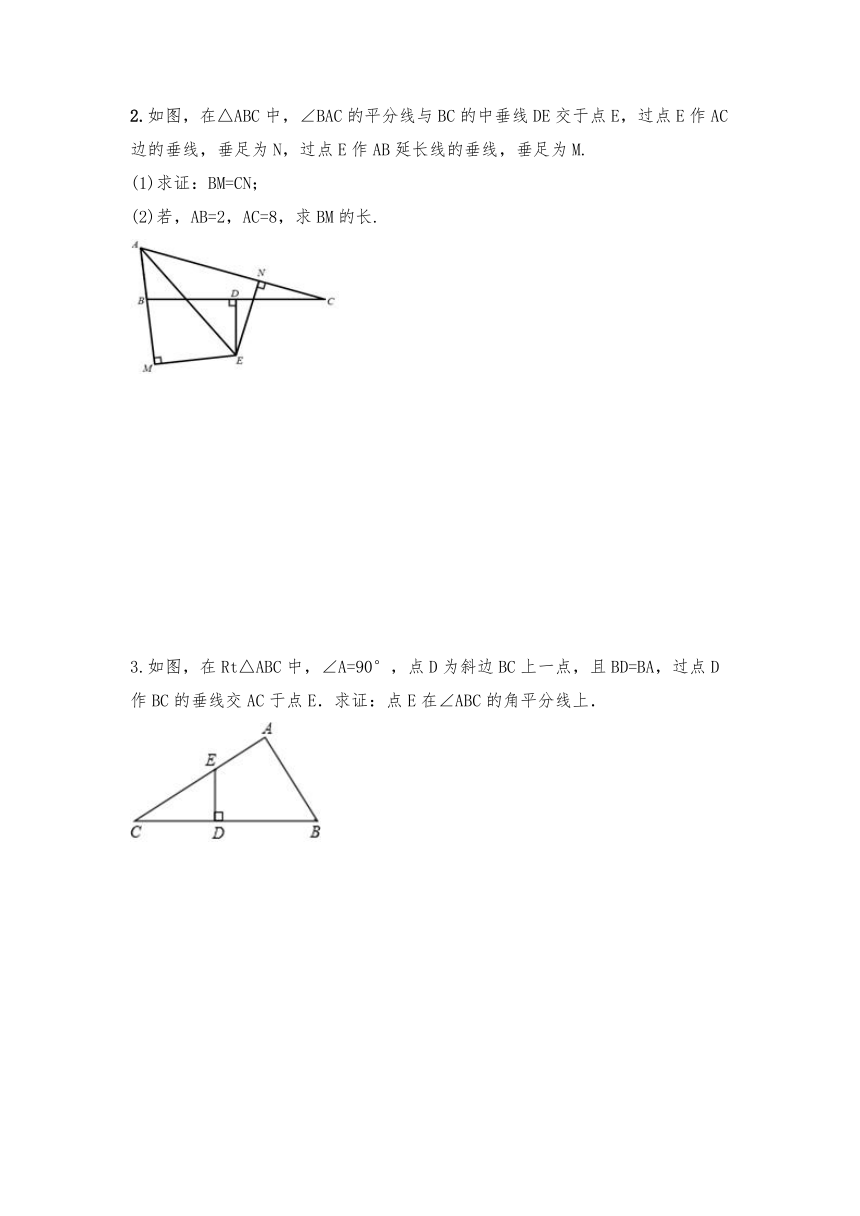
2.如图,在△ABC中,∠BAC的平分线与BC的中垂线DE交于点E,过点E作AC边的垂线,垂足为N,过点E作AB延长线的垂线,垂足为M.
(1)求证:BM=CN;
(2)若,AB=2,AC=8,求BM的长.
3.如图,在Rt△ABC中,∠A=90°,点D为斜边BC上一点,且BD=BA,过点D作BC的垂线交AC于点E.求证:点E在∠ABC的角平分线上.
4.如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
(1)求证:△BCE≌△DCF;
(2)求证:AB+AD=2AE.
5.如图,已知在中,点在边上,且.
(1)用尺规作图法,作的平分线,交于点;(保留作图痕迹,不要求写作法)
(2)在(1)的条件下,连接.求证:.
6.如图所示,在△ABC中,按以下步骤作图:①以点B为圆心,任意长为半径作弧,分别交BA、BC于点M、N;再以点N为圆心,MN长为半径作弧交前面的弧于点F,作射线BF交AC的延长线于点E.
②以点B为圆心,BA长为半径作弧交BE于点D,连接CD.
请你观察图形,解答下列问题:
(1)求证:△ABC≌△DBC;
(2)若∠A=100°,∠E=50°,求∠ACB的度数.
答案
一、选择题
1.D.2.C.3.B.4.D.5.C.6.B.7.B.8.C.
9.A.10.D.11.A.
二、填空题
1.4
2.
3.3
三、解答题
1.解:(1)过A作AE⊥BC于E,
∵点D是BC边上的中点,
∴BD=DC,
∴SABD:S△ACD=(×BD×AE):(×CD×AE)=1:1,
故答案为:1:1;
(2)过D作DE⊥AB于E,DF⊥AC于F,
∵AD为∠BAC的角平分线,
∴DE=DF,
∵AB=m,AC=n,
∴SABD:S△ACD=(×AB×DE):(×AC×DF)=m:n;
(3)∵AD=DE,
∴由(1)知:S△ABD:S△EBD=1:1,
∵S△BDE=6,
∴S△ABD=6,
∵AC=2,AB=4,AD平分∠CAB,
∴由(2)知:S△ABD:S△ACD=AB:AC=4:2=2:1,
∴S△ACD=3,
∴S△ABC=3+6=9,
故答案为:9.
2.证明:连接BE,CE,如图,
∴DE是BC的垂直平分线,
∴BE=CE,
∵AE是∠BAC的平分线,EM⊥AB,EN⊥AC,
∴EM=EN,
在Rt△BME和Rt△CNE中,
∴Rt△BME≌Rt△CNE(HL),
∴BM=CN
(2)由(1)得:EM=EN,
在Rt△AME和Rt△ANE中,
∴Rt△AME≌Rt△ANE(HL),
∴AM=AN,又∵AM=
AB+BM,
AN=
AC-CN
∴AB+BM=AC-CN
∴2+
BM=8-CN,
又∵BM=CN
∴BM=CN
=3
3.证明:连接BE,
∵ED⊥BC,
∴∠BDE=∠A=90°.
在Rt△ABE和Rt△DBE中
∵,
∴Rt△ABE≌Rt△DBE(HL).
∴∠ABE=∠DBE.
∴点E在∠ABC的角平分线上.
4.(1)证明:∵AC是角平分线,CE⊥AB于E,CF⊥AD于F,
∴CE=CF,∠F=∠CEB=90°,
在Rt△BCE和Rt△DCF中,
∴△BCE≌△DCF;
(2)解:∵CE⊥AB于E,CF⊥AD于F,
∴∠F=∠CEA=90°,
在Rt△FAC和Rt△EAC中,,
∴Rt△FAC≌Rt△EAC,
∴AF=AE,
∵△BCE≌△DCF,
∴BE=DF,
∴AB+AD=(AE+BE)+(AF﹣DF)=AE+BE+AE﹣DF=2AE.
5.(1)如图,射线AP为所求作的图形;
(2)∵CP是∠ACB的平分线,如图:
∴∠1=∠2,
在△ABP和△ADP中,
,
∴△ABP△ADP(SAS),
∴PD=PB.
6.(1)如图所示,连接MN,NF,
由作图可得,BM=BF,MN=FN,BN=BN,
∴△BMN≌△BFN(SSS),
∴∠ABC=∠DBC,
又∵AB=DB,BC=BC,
∴△ABC≌△DBC(SAS);
(2)∵∠A=100°,∠E=50°,
∴∠ABE=30°,
∴∠ABC=∠ABD=15°,
∴∠ACB=180°-∠A-∠ABC=180°-100°-15°=65°.
一、选择题
1.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为( )
A.
B.
C.3
D.
2.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为用A、B.下列结论中不一定成立的是(
)
A.PA=PE
B.PO平分∠APB
C.AB垂直平分OP
D.OA=OB
3.如图,在中,,以顶点为圆心,适当长为半径画弧,分别交,于点,,再分别以点,为圆心,大于的长为半径画弧,两弧交于点,作射线交边于点,若,,则的面积是
(
)
A.15
B.30
C.45
D.60
4.如图,a、b、c三条公路的位置相交成三角形,现决定在三条公路之间建一购物超市,使超市到三条公路的距离相等,则超市应建在(
)
A.三角形两边高线的交点处
B.三角形两边中线的交点处
C.∠α的平分线上
D.∠α和∠β的平分线的交点处
5.如图,在中,,以点为圆心,适当长为半径画弧,分别交于点,再分别以点为圆心,大于为半径画弧,两弧交于点,作射线交边于点,则的面积是( )
A.
B.
C.
D.
6.如图所示,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=3cm,那么AE+DE等于(
)
A.2cm
B.3cm
C.4cm
D.5cm
7.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为( )
A.11
B.5.5
C.7
D.3.5
8.如图,在△ABC中,E为AC的中点,AD平分∠BAC,BA:CA=2:3,AD与BE相交于点O,若△OAE的面积比△BOD的面积大1,则△ABC的面积是( )
A.8
B.9
C.10
D.11
9.如图尺规作业,为的平分线,这样的作法依据是( )
A.
B.
C.
D.
10.如图,△ABC
中,点
E,F,G
分别在
BC,AC,AB
上,AE
与
BF
交于点
O,且点
O
在
CG
上,根据尺规作图的痕迹,判断下列说法不正确的是(
)
A.AE,BF
是△ABC
的角平分线
B.点
O
到△ABC
三边的距离相等
C.CG
也是△ABC
的一条角平分线
D.AO=BO=CO
11.如图,在中,尺规作图如下:在射线、上,分别截取、,使;分别以点和点为圆心、大于的长为半径作弧,两弧相交于点;作射线,连结、.下列结论不一定成立的是(
)
A.
B.
C.
D.
二、填空题
1.如图,∠B=∠C=90°,DM平分∠ADC,AM平分∠DAB,CB=8,则点M到BC的距离_______.
2.如图,的三边
的长分别为,其三条角平分线交于点,则=______.
3.如图,BD平分∠ABC,DE⊥AB于E,DF⊥BC于F,AB=6,BC=8.若S△ABC=21,则DE=________.
三、解答题
1.如图,在△ABC中,D是BC边上的点(不与点B,C重合),连结AD
(1)如图1,当点D是BC边上的中点时,则S△ABD:S△ACD=_________(直接写出答案)
(2)如图2,当AD是∠BAC的平分线时,若AB=m,AC=n,S△ABD:S△ACD=_________
(用含m,n的代数式表示).
(3)如图3,AD平分∠BAC,延长AD到E,使得AD=DE,连结BE,如果AC=2,AB=4,S△BDE
=6,求△ABC的面积.
2.如图,在△ABC中,∠BAC的平分线与BC的中垂线DE交于点E,过点E作AC边的垂线,垂足为N,过点E作AB延长线的垂线,垂足为M.
(1)求证:BM=CN;
(2)若,AB=2,AC=8,求BM的长.
3.如图,在Rt△ABC中,∠A=90°,点D为斜边BC上一点,且BD=BA,过点D作BC的垂线交AC于点E.求证:点E在∠ABC的角平分线上.
4.如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
(1)求证:△BCE≌△DCF;
(2)求证:AB+AD=2AE.
5.如图,已知在中,点在边上,且.
(1)用尺规作图法,作的平分线,交于点;(保留作图痕迹,不要求写作法)
(2)在(1)的条件下,连接.求证:.
6.如图所示,在△ABC中,按以下步骤作图:①以点B为圆心,任意长为半径作弧,分别交BA、BC于点M、N;再以点N为圆心,MN长为半径作弧交前面的弧于点F,作射线BF交AC的延长线于点E.
②以点B为圆心,BA长为半径作弧交BE于点D,连接CD.
请你观察图形,解答下列问题:
(1)求证:△ABC≌△DBC;
(2)若∠A=100°,∠E=50°,求∠ACB的度数.
答案
一、选择题
1.D.2.C.3.B.4.D.5.C.6.B.7.B.8.C.
9.A.10.D.11.A.
二、填空题
1.4
2.
3.3
三、解答题
1.解:(1)过A作AE⊥BC于E,
∵点D是BC边上的中点,
∴BD=DC,
∴SABD:S△ACD=(×BD×AE):(×CD×AE)=1:1,
故答案为:1:1;
(2)过D作DE⊥AB于E,DF⊥AC于F,
∵AD为∠BAC的角平分线,
∴DE=DF,
∵AB=m,AC=n,
∴SABD:S△ACD=(×AB×DE):(×AC×DF)=m:n;
(3)∵AD=DE,
∴由(1)知:S△ABD:S△EBD=1:1,
∵S△BDE=6,
∴S△ABD=6,
∵AC=2,AB=4,AD平分∠CAB,
∴由(2)知:S△ABD:S△ACD=AB:AC=4:2=2:1,
∴S△ACD=3,
∴S△ABC=3+6=9,
故答案为:9.
2.证明:连接BE,CE,如图,
∴DE是BC的垂直平分线,
∴BE=CE,
∵AE是∠BAC的平分线,EM⊥AB,EN⊥AC,
∴EM=EN,
在Rt△BME和Rt△CNE中,
∴Rt△BME≌Rt△CNE(HL),
∴BM=CN
(2)由(1)得:EM=EN,
在Rt△AME和Rt△ANE中,
∴Rt△AME≌Rt△ANE(HL),
∴AM=AN,又∵AM=
AB+BM,
AN=
AC-CN
∴AB+BM=AC-CN
∴2+
BM=8-CN,
又∵BM=CN
∴BM=CN
=3
3.证明:连接BE,
∵ED⊥BC,
∴∠BDE=∠A=90°.
在Rt△ABE和Rt△DBE中
∵,
∴Rt△ABE≌Rt△DBE(HL).
∴∠ABE=∠DBE.
∴点E在∠ABC的角平分线上.
4.(1)证明:∵AC是角平分线,CE⊥AB于E,CF⊥AD于F,
∴CE=CF,∠F=∠CEB=90°,
在Rt△BCE和Rt△DCF中,
∴△BCE≌△DCF;
(2)解:∵CE⊥AB于E,CF⊥AD于F,
∴∠F=∠CEA=90°,
在Rt△FAC和Rt△EAC中,,
∴Rt△FAC≌Rt△EAC,
∴AF=AE,
∵△BCE≌△DCF,
∴BE=DF,
∴AB+AD=(AE+BE)+(AF﹣DF)=AE+BE+AE﹣DF=2AE.
5.(1)如图,射线AP为所求作的图形;
(2)∵CP是∠ACB的平分线,如图:
∴∠1=∠2,
在△ABP和△ADP中,
,
∴△ABP△ADP(SAS),
∴PD=PB.
6.(1)如图所示,连接MN,NF,
由作图可得,BM=BF,MN=FN,BN=BN,
∴△BMN≌△BFN(SSS),
∴∠ABC=∠DBC,
又∵AB=DB,BC=BC,
∴△ABC≌△DBC(SAS);
(2)∵∠A=100°,∠E=50°,
∴∠ABE=30°,
∴∠ABC=∠ABD=15°,
∴∠ACB=180°-∠A-∠ABC=180°-100°-15°=65°.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
