北师大版八年级数学下册一课一练试题 1.1《等腰三角形》习题(Word版 含答案)
文档属性
| 名称 | 北师大版八年级数学下册一课一练试题 1.1《等腰三角形》习题(Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 389.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-12 00:00:00 | ||
图片预览



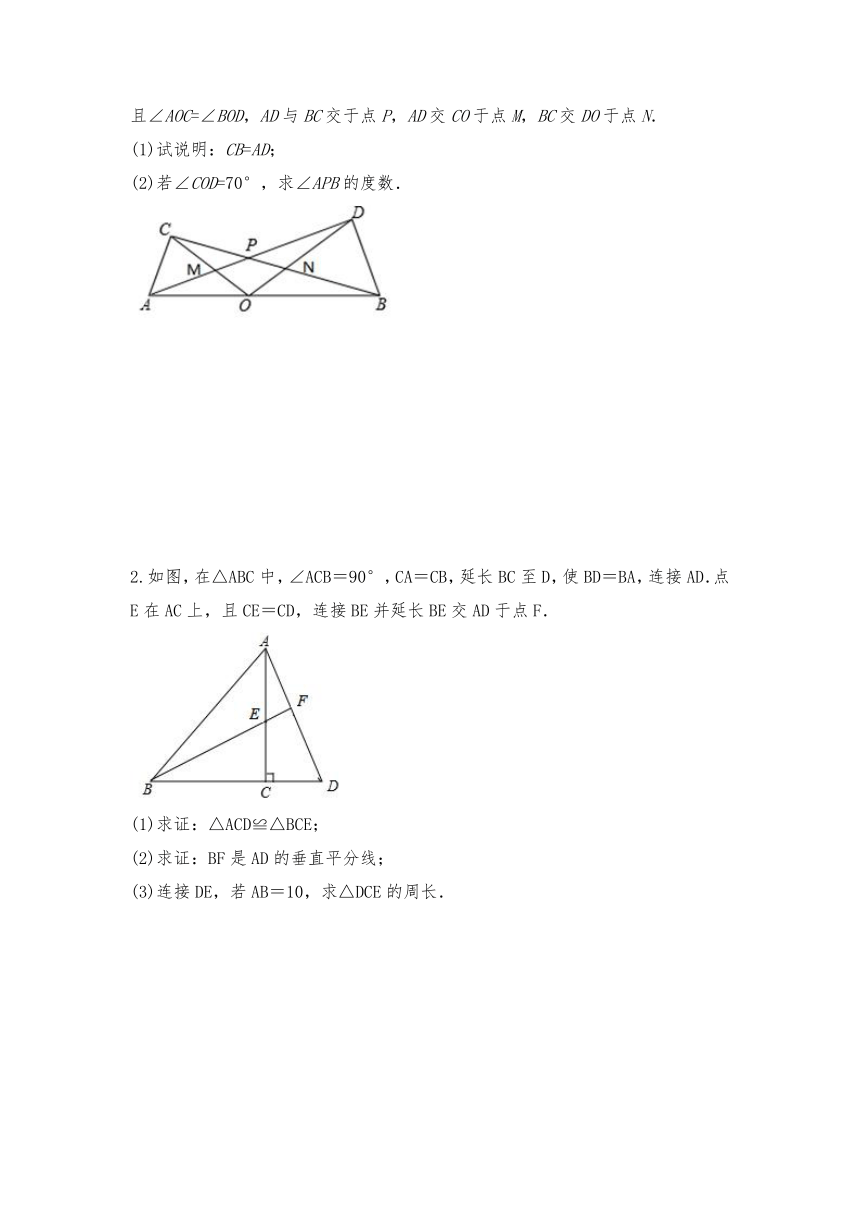
文档简介
1.1《等腰三角形》习题
一、选择题
1.如图,△ABC中,AB=AC,腰AB的垂直平分线DE交AB于点E,交AC于点D,且∠DBC=15°,则∠A的度数是
(
)
A.50°
B.36°
C.40°
D.45°
2.如图,在△ABC
中,AB=AC,∠C=70°,△AB′C′与△ABC
关于直线
EF对称,∠CAF=10°,连接
BB′,则∠ABB′的度数是(
)
A.30°
B.35°
C.40°
D.45°
3.如图,中,是的角平分线,的垂直平分线分别交于点,则下列结论不一定成立的是(
)
A.
B.
C.
D.
4.如图所示,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于(
)
A.30°
B.40°
C.45°
D.36°
5.如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的底角度数是( )
A.()n?75°
B.()n﹣1?65°
C.()n﹣1?75°
D.()n?85°
6.如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是( )
A.20°
B.35°
C.40°
D.70°
7.如图,在中,,,AB的垂直平分线交AB于点E,交BC于点F,连接AF,则的度数(
)
A.
B.
C.
D.
8.如图“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D、E可在槽中滑动,若∠BDE=72°,则∠CDE的度数是( )
A.63°
B.65°
C.75°
D.84°
9.如图,已知∠AOB=10°,且OC=CD=DE=EF=FG=GH,则∠BGH=
(
)
A.50°
B.60°
C.70°
D.80°
10.如图,已知C是线段AB上的任意一点(端点除外),分别以AC、BC为边并且在AB的同一侧作等边△ACD和等边△BCE,连接AE交CD于M,连接BD交CE于N.给出以下三个结论:①AE=BD
;
②CN=CM;
③MN∥AB;
④∠CDB=∠NBE.
其中正确结论的个数是(
)
A.4
B.3
C.2
D.1
11.如图,在四边形ABCD中,对角线AC与BD相交于点E,若AC平分∠DAB,且AB=AC,AC=AD,有四个结论:①AC⊥BD;②BC=DC;③△ABC≌△ADC;④△ABD
是等边三角形.其中正确的是(
)
A.①②③
B.①②④
C.②③④
D.①③④
二、填空题
1.如图,△DAC和△EBC均是等边三角形,A、C、B三点共线,AE与BD相交于点P,AE与BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②∠DPA=60°;③AC=DN;④EM=BN;⑤DC∥EB,其中正确结论是__________(填序号)
2.如图,和都是等边三角形,∠EBD=78°,则∠AEB=_____度.
3.如图,在等边三角形ABC中,点D在边AB上,点E在边AC上,将△ADE折叠,使点A落在BC边上的点F处,则∠BDF+∠CEF=_____.
4.如图,中,,,,,平分,与相交于点,则的长等于_____.
三、解答题
1.如图,点O为线段AB上的任意一点(不于A、B重合),分别以AO,BO为一腰在AB的同侧作等腰△AOC和△BOD,OA=OC,OB=OD,∠AOC与∠BOD都是锐角,且∠AOC=∠BOD,AD与BC交于点P,AD交CO于点M,BC交DO于点N.
(1)试说明:CB=AD;
(2)若∠COD=70°,求∠APB的度数.
2.如图,在△ABC中,∠ACB=90°,CA=CB,延长BC至D,使BD=BA,连接AD.点E在AC上,且CE=CD,连接BE并延长BE交AD于点F.
(1)求证:△ACD≌△BCE;
(2)求证:BF是AD的垂直平分线;
(3)连接DE,若AB=10,求△DCE的周长.
3.如图所示,在四边形中,,,,平分交边于点,求的长.
4.如图,已知等腰△ABC顶角∠A=36°.
(1)尺规作图:在AC上作一点D,使AD=BD;(保留作图痕迹,不必写作法和证明)
(2)求证:△BCD是等腰三角形.
5.如图,在和中,,,AC与BD相交于点O.
(1)求证:;
(2)是何种三角形?
6.已知∠MAN=30°,点B在射线AM上,且
AB=6,点C在射线AN上.
(1)若△ABC是直角三角形,求AC的长;
(2)若△ABC是等腰三角形,则满足条件的C点有
个;
(3)设BC=x,当△ABC唯一确定时,
直接写出的取值范围.
7.如图,已知ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F.
(1)求证:BE=AD;
(2)求∠BFD的度数.
8.如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,两线相交于F点.
(1)若∠BAC=60°,∠C=70°,求∠AFB的大小;
(2)若D是BC的中点,∠ABE=30°,求证:△ABC是等边三角形.
答案
一、选择题
1.A.2.C.3.D.4.D.5.C.6.B.7.D.
8.D.9.B.10.A.11.A.
二、填空题
1.①②④⑤
2.138
3.120°
4.3
三、解答题
1.
(1)∵∠AOC=∠BOD,
∴∠AOD=∠COB,
又∵OA=OC,OB=OD,
∴△AOD≌△COB(SAS),
∴CB=AD;
(2)∵∠COD=70°,
∴∠AOC=∠BOD==55°,
∴∠AOD=∠COD+∠BOD=125°=∠COB,
∵△AOD≌△COB,
∴∠DAO=∠BCO,
∴∠DAO+∠CBO=∠BCO+∠CBO,
∴180°-∠APB=180°-∠COB,
∴∠APB=∠COB=125°.
2.(1)证明:
∵∠ACB=90°,CD是BC延长线,
∴∠ACD=∠ACB=90°.
在△ACD和△BCE中,,
∴△ACD≌△BCE(SAS).
(2)由(1)知△ACD≌△BCE则∠CAD=∠CBE,
又∵∠AEF=∠BEC,
∴在△AEF与△BEC中∠AFE=∠BCE=90°,
∴BF⊥AD,
又∵BD=BA,
∴BF是AD的垂直平分线.
(3)∵EF是AD的垂直平分线,
∴EA=ED,
又∵BC=AC,AB=BD=10,
∴△DEC的周长=ED+EC+CD=AC+CD=BC+CD=AB=10.
3.解:,
∵∠DAE=∠BEA
平分,
.
,
.
.
4.(1)如图1,作AB的垂直平分线,分别以点A、B为圆心,以大于为半径在AB上方画弧,在AB上方两圆弧交点为点M,分别以点A、B为圆心以大于为半径在AB下方画弧,在AB下方两圆弧交点为点N.过点M、N作直线MN,交AC于点D,点D即为所求.
(2)∵在等腰△ABC顶角∠A=36°
∴
∵AD=BD
∴∠ABD=∠A=36°
则∠DBC=36°
在△BCD中∠ACB=72°
∠DBC=36°
∠BDC=72°=∠ACB
∴△BCD是等腰三角形
5.(1)∵∠A=∠D=90°,
∴在Rt△ABC和Rt△DCB中,,
∴Rt△ABC≌Rt△DCB(HL);
(2)△OBC是等腰三角形,
理由:∵Rt△ABC≌Rt△DCB,
∴∠ACB=∠DBC,
∴OB=OC,
∴△OBC是等腰三角形.
6.(1)当∠ABC=90°时,如图所示,
∵∠A=30°
∴BC=
∴设BC=x,则AC=2x
在Rt△ABC中,由勾股定理得
解得x=
∴AC=
当∠ACB=90°时,如图所示,
∵∠A=30°
∴BC=
∴AC=
(2)当AB为腰时,等腰三角形有两个,如图,
当AB为底时,等腰三角形有1个,如图
∴△ABC是等腰三角形,则满足条件的C点有3个
(3)根据三角形三边关系可知,△ABC唯一确定时,由(1)、(2)得,BC=3或BC≥6.
7.解:(1)∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠C=60°,
又∵AE=CD,
∴△ABE≌△CAD(SAS),
∴BE=AD;
(2)∵△ABE≌△CAD,
∴∠ABE=∠CAD,
∴∠BFD=∠ABE+∠BAD=∠CAD+∠BAD=∠BAC=60°.
8.(1)∵∠BAC=60°,∠C=70°,
∴∠ABC=180°﹣60°﹣70°=50°,
∵BE平分∠ABC,
∴∠FBD=∠ABC=25°,
∵AD⊥BC,
∴∠BDF=90°,
∴∠AFB=∠FBD+∠BDF=115°.
(2)证明:∵∠ABE=30°,BE平分∠ABC,
∴∠ABC=60°,
∵BD=DC,AD⊥BC,
∴AB=AC,
∴△ABC是等边三角形.
一、选择题
1.如图,△ABC中,AB=AC,腰AB的垂直平分线DE交AB于点E,交AC于点D,且∠DBC=15°,则∠A的度数是
(
)
A.50°
B.36°
C.40°
D.45°
2.如图,在△ABC
中,AB=AC,∠C=70°,△AB′C′与△ABC
关于直线
EF对称,∠CAF=10°,连接
BB′,则∠ABB′的度数是(
)
A.30°
B.35°
C.40°
D.45°
3.如图,中,是的角平分线,的垂直平分线分别交于点,则下列结论不一定成立的是(
)
A.
B.
C.
D.
4.如图所示,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于(
)
A.30°
B.40°
C.45°
D.36°
5.如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的底角度数是( )
A.()n?75°
B.()n﹣1?65°
C.()n﹣1?75°
D.()n?85°
6.如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是( )
A.20°
B.35°
C.40°
D.70°
7.如图,在中,,,AB的垂直平分线交AB于点E,交BC于点F,连接AF,则的度数(
)
A.
B.
C.
D.
8.如图“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D、E可在槽中滑动,若∠BDE=72°,则∠CDE的度数是( )
A.63°
B.65°
C.75°
D.84°
9.如图,已知∠AOB=10°,且OC=CD=DE=EF=FG=GH,则∠BGH=
(
)
A.50°
B.60°
C.70°
D.80°
10.如图,已知C是线段AB上的任意一点(端点除外),分别以AC、BC为边并且在AB的同一侧作等边△ACD和等边△BCE,连接AE交CD于M,连接BD交CE于N.给出以下三个结论:①AE=BD
;
②CN=CM;
③MN∥AB;
④∠CDB=∠NBE.
其中正确结论的个数是(
)
A.4
B.3
C.2
D.1
11.如图,在四边形ABCD中,对角线AC与BD相交于点E,若AC平分∠DAB,且AB=AC,AC=AD,有四个结论:①AC⊥BD;②BC=DC;③△ABC≌△ADC;④△ABD
是等边三角形.其中正确的是(
)
A.①②③
B.①②④
C.②③④
D.①③④
二、填空题
1.如图,△DAC和△EBC均是等边三角形,A、C、B三点共线,AE与BD相交于点P,AE与BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②∠DPA=60°;③AC=DN;④EM=BN;⑤DC∥EB,其中正确结论是__________(填序号)
2.如图,和都是等边三角形,∠EBD=78°,则∠AEB=_____度.
3.如图,在等边三角形ABC中,点D在边AB上,点E在边AC上,将△ADE折叠,使点A落在BC边上的点F处,则∠BDF+∠CEF=_____.
4.如图,中,,,,,平分,与相交于点,则的长等于_____.
三、解答题
1.如图,点O为线段AB上的任意一点(不于A、B重合),分别以AO,BO为一腰在AB的同侧作等腰△AOC和△BOD,OA=OC,OB=OD,∠AOC与∠BOD都是锐角,且∠AOC=∠BOD,AD与BC交于点P,AD交CO于点M,BC交DO于点N.
(1)试说明:CB=AD;
(2)若∠COD=70°,求∠APB的度数.
2.如图,在△ABC中,∠ACB=90°,CA=CB,延长BC至D,使BD=BA,连接AD.点E在AC上,且CE=CD,连接BE并延长BE交AD于点F.
(1)求证:△ACD≌△BCE;
(2)求证:BF是AD的垂直平分线;
(3)连接DE,若AB=10,求△DCE的周长.
3.如图所示,在四边形中,,,,平分交边于点,求的长.
4.如图,已知等腰△ABC顶角∠A=36°.
(1)尺规作图:在AC上作一点D,使AD=BD;(保留作图痕迹,不必写作法和证明)
(2)求证:△BCD是等腰三角形.
5.如图,在和中,,,AC与BD相交于点O.
(1)求证:;
(2)是何种三角形?
6.已知∠MAN=30°,点B在射线AM上,且
AB=6,点C在射线AN上.
(1)若△ABC是直角三角形,求AC的长;
(2)若△ABC是等腰三角形,则满足条件的C点有
个;
(3)设BC=x,当△ABC唯一确定时,
直接写出的取值范围.
7.如图,已知ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F.
(1)求证:BE=AD;
(2)求∠BFD的度数.
8.如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,两线相交于F点.
(1)若∠BAC=60°,∠C=70°,求∠AFB的大小;
(2)若D是BC的中点,∠ABE=30°,求证:△ABC是等边三角形.
答案
一、选择题
1.A.2.C.3.D.4.D.5.C.6.B.7.D.
8.D.9.B.10.A.11.A.
二、填空题
1.①②④⑤
2.138
3.120°
4.3
三、解答题
1.
(1)∵∠AOC=∠BOD,
∴∠AOD=∠COB,
又∵OA=OC,OB=OD,
∴△AOD≌△COB(SAS),
∴CB=AD;
(2)∵∠COD=70°,
∴∠AOC=∠BOD==55°,
∴∠AOD=∠COD+∠BOD=125°=∠COB,
∵△AOD≌△COB,
∴∠DAO=∠BCO,
∴∠DAO+∠CBO=∠BCO+∠CBO,
∴180°-∠APB=180°-∠COB,
∴∠APB=∠COB=125°.
2.(1)证明:
∵∠ACB=90°,CD是BC延长线,
∴∠ACD=∠ACB=90°.
在△ACD和△BCE中,,
∴△ACD≌△BCE(SAS).
(2)由(1)知△ACD≌△BCE则∠CAD=∠CBE,
又∵∠AEF=∠BEC,
∴在△AEF与△BEC中∠AFE=∠BCE=90°,
∴BF⊥AD,
又∵BD=BA,
∴BF是AD的垂直平分线.
(3)∵EF是AD的垂直平分线,
∴EA=ED,
又∵BC=AC,AB=BD=10,
∴△DEC的周长=ED+EC+CD=AC+CD=BC+CD=AB=10.
3.解:,
∵∠DAE=∠BEA
平分,
.
,
.
.
4.(1)如图1,作AB的垂直平分线,分别以点A、B为圆心,以大于为半径在AB上方画弧,在AB上方两圆弧交点为点M,分别以点A、B为圆心以大于为半径在AB下方画弧,在AB下方两圆弧交点为点N.过点M、N作直线MN,交AC于点D,点D即为所求.
(2)∵在等腰△ABC顶角∠A=36°
∴
∵AD=BD
∴∠ABD=∠A=36°
则∠DBC=36°
在△BCD中∠ACB=72°
∠DBC=36°
∠BDC=72°=∠ACB
∴△BCD是等腰三角形
5.(1)∵∠A=∠D=90°,
∴在Rt△ABC和Rt△DCB中,,
∴Rt△ABC≌Rt△DCB(HL);
(2)△OBC是等腰三角形,
理由:∵Rt△ABC≌Rt△DCB,
∴∠ACB=∠DBC,
∴OB=OC,
∴△OBC是等腰三角形.
6.(1)当∠ABC=90°时,如图所示,
∵∠A=30°
∴BC=
∴设BC=x,则AC=2x
在Rt△ABC中,由勾股定理得
解得x=
∴AC=
当∠ACB=90°时,如图所示,
∵∠A=30°
∴BC=
∴AC=
(2)当AB为腰时,等腰三角形有两个,如图,
当AB为底时,等腰三角形有1个,如图
∴△ABC是等腰三角形,则满足条件的C点有3个
(3)根据三角形三边关系可知,△ABC唯一确定时,由(1)、(2)得,BC=3或BC≥6.
7.解:(1)∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠C=60°,
又∵AE=CD,
∴△ABE≌△CAD(SAS),
∴BE=AD;
(2)∵△ABE≌△CAD,
∴∠ABE=∠CAD,
∴∠BFD=∠ABE+∠BAD=∠CAD+∠BAD=∠BAC=60°.
8.(1)∵∠BAC=60°,∠C=70°,
∴∠ABC=180°﹣60°﹣70°=50°,
∵BE平分∠ABC,
∴∠FBD=∠ABC=25°,
∵AD⊥BC,
∴∠BDF=90°,
∴∠AFB=∠FBD+∠BDF=115°.
(2)证明:∵∠ABE=30°,BE平分∠ABC,
∴∠ABC=60°,
∵BD=DC,AD⊥BC,
∴AB=AC,
∴△ABC是等边三角形.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
