北师大版七上数学4.4 角的比较课件(共27张)
文档属性
| 名称 | 北师大版七上数学4.4 角的比较课件(共27张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 00:00:00 | ||
图片预览






文档简介
(共27张PPT)
第四章
基本平面图形
4.4
角的比较
1
课堂讲解
角的比较
角的和差
角的平分线
2
课时流程
逐点
导讲练
课堂小结
作业提升
问题:有一天学生张虎和王鹏各带了一把折扇(如图),
下面是他们的一段对话:
张:我的折扇大一些,所以我的折扇的角
也大一些.
王:我的折扇长一些,所以我的折扇的角也大一些.
同学们,你们有办法帮他们进行判断吗?
A
B
C
D
E
F
怎样比较∠ABC和∠DEF的大小?
1
知识点
角的比较
知1-导
角的比较:
请同学们任意画出两个角比较一下,并讨论你们的比较方法:
B
A
C
E
D
F
你的方法有:
(1)度量法比较
(2)叠合法比较
知1-讲
一.
度量法
1、对“中”—角的顶点对量角器的中心
3、读数—读出角的另一边所对的度数
2、重合—角的一边与量角器的0°刻度线重合
B
C
A
F
E
D
700
∠ABC
>
∠DEF
30°
知1-讲
A
B
O
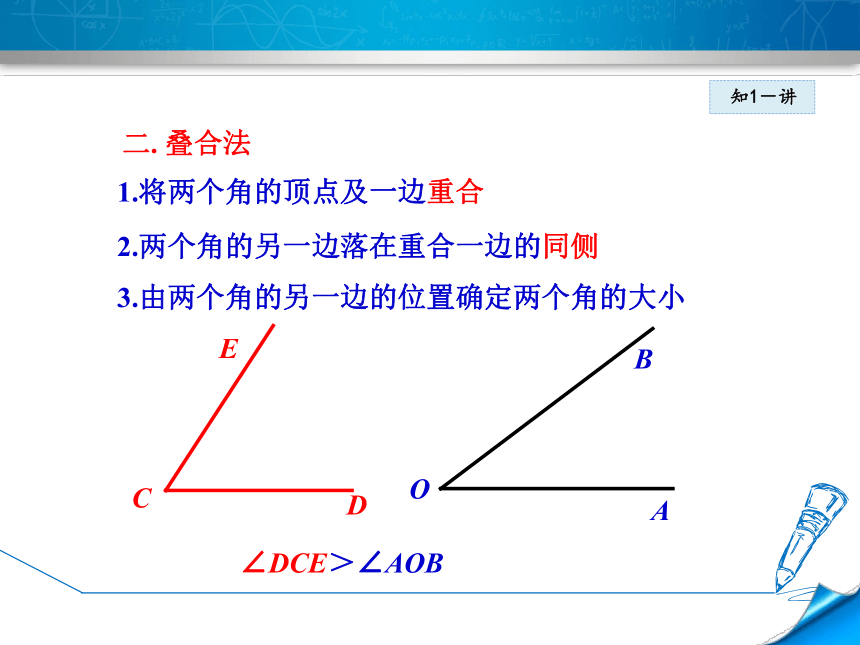
1.将两个角的顶点及一边重合
2.两个角的另一边落在重合一边的同侧
3.由两个角的另一边的位置确定两个角的大小
二.
叠合法
C
D
E
∠DCE>∠AOB
知1-讲
O
A
B
D
C
E
A
O
B
C
D
E
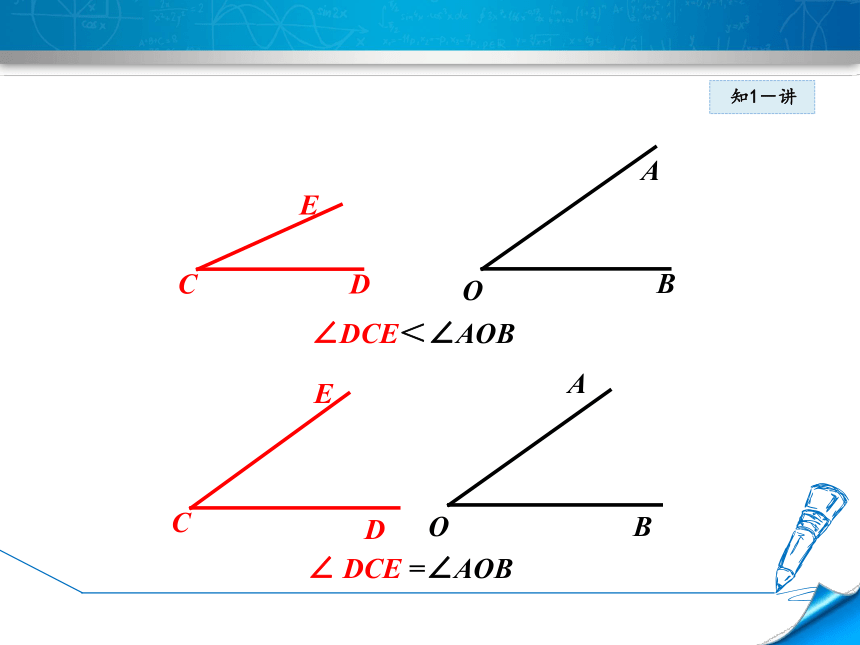
∠DCE<∠AOB
∠
DCE
=∠AOB
知1-讲
例1
根据图,回答下列问题:
(1)比较∠FOD与∠FOE的大小;
(2)借助三角尺比较∠DOE
与
∠DOF
的大小.
导引:(1)中两个角有重合边和重合顶点,利用叠合法
比较一目了然,因为OD
边在∠FOE的内部,
所以有∠FOD
<∠FOE.
(2)∠DOE明显大于
45°,而∠DOF
明显小于
45°,故有∠DOE
>∠DOF.
知1-讲
解:(1)∠FOD<∠FOE.
(2)用含有45°角的三角尺比较,可得∠DOE>
45°,∠DOF<45°,所以∠DOE>∠DOF.
总
结
知1-讲
用叠合法比较角的大小时,一定要将两个角的
另一边落在重合边的同侧.两边都不重合,或有一
边重合但另一边在重合边的异侧的两角,可通过度
量法比较大小.
1
在∠AOB的内部任取一点C,作射线OC,那么
有( )
A.∠AOC=∠BOC B.∠AOC>∠BOC
C.∠BOC>∠AOB
D.∠AOB>∠AOC
如图,如果∠AOB=∠COD,那么( )
A.∠1>∠2
B.∠1=∠2
C.∠1<∠2
D.以上都不对
知1-练
2
B
B
知2-讲
2
知识点
角的和差
思考
如图,图中共有几个角?
它们之间有
什么关系?
图中,∠AOC
是∠AOB
与∠BOC
的和,记作
∠AOC=∠AOB
+
∠BOC.
∠AOB
是∠AOC
与∠BOC
的差,记作∠AOB
=
∠AOC
-∠BOC.
类似地,∠AOC
-∠AOB=____________.
∠BOC
例3
如图,∠AOB=48°,∠1=
32°24′,求∠2的度数.
导引:要求∠2的度数,就是要把它转
化为用已知角∠1的关系式来表示.根据图形可
知,∠1+∠2=∠AOB,因此∠2=∠AOB-∠1.
解:因为∠AOB=48°,∠1=32°24′,
所以∠2=48°-32°24′
=47°60′-32°24′=15°36′.
知2-讲
例4
如图,OC是∠AOD的平分线,
OE是∠BOD的平分线.
(1)如果∠AOB=130°,那么
∠COE是多少度?
(2)在(1)的条件下,如果∠DOC
=20°,那么∠BOE是多少度?
导引:(1)由已知可知∠DOC=
∠AOD,∠DOE=
∠BOD.由于∠COE=∠DOC+∠DOE,因此,
∠COE=
∠AOD+
∠BOD=
∠AOB.
(2)结合(1)的结论可求出∠DOE的度数,从而求出
∠BOE的度数.
知2-讲
解:(1)因为OC平分∠AOD,
所以∠DOC=
∠AOD.
因为OE平分∠BOD,
所以∠DOE=
∠BOD.
所以∠COE=∠DOC+∠DOE=
(∠AOD+∠BOD)
∠AOB=
×130°=65°.
(2)由(1)可知∠COE=65°,因为∠DOC=20°,
所以∠DOE=∠COE-∠DOC=45°.
因为OE平分∠BOD,
所以∠BOE=∠DOE=45°.
知2-讲
总
结
知2-讲
(1)利用角平分线进行计算时,要灵活运用角平分
线的几种不同表达方式.
(2)在计算角的大小时,常常要用到等量代换,用
已知角代替与它相等的未知角.
1
如图,∠AOD-∠AOC=( )
A.∠AOC
B.∠BOC
C.∠BOD
D.∠COD
(中考?滨州)借助一副三角尺,你能画出下面哪个
度数的角( )
A.65°
B.75°
C.85°
D.95°
知2-练
2
D
B
(中考?辽宁)如图,已知直线AB,CD相交
于点O,OA平分∠EOC,∠EOC=110°,则
∠BOD的度数是( )
A.25°
B.35°
C.45°
D.55°
知2-练
3
D
3
知识点
角的平分线
知3-导
如图,在透明纸上画一个角,沿着顶点对折,
使角的两边重合.∠AOC被折痕OB分成的两个角有
什么关系?
知3-讲
1.定义:一般地,从一个角的顶点出发,把这个角分
成两个相等的角的射线,叫做这个角的平分线.
要点精析:
(1)角平分线是在角的内部从角的顶点引出的一条射
线,不是直线或线段;
(2)角平分线把角分成了两个相等的角.
知3-讲
例2
如图,∠1=∠2,∠3=∠4,则
下列结论:①AD平分∠BAF;
②AF平分∠DAC;③AE平分
∠DAF;④AF平分∠BAC;
⑤AE平分∠BAC中,正确的有( )
A.4个 B.3个
C.2个
D.1个
导引:由角的平分线的几何表示可知:当∠1=∠2时,
AE平分∠DAF;再由∠3=∠4可得∠1+∠3=
∠2+∠4,即∠BAE=∠CAE,因此AE平分
∠BAC.
C
总
结
知3-讲
判断一条射线是不是角的平分线,只要看这
条射线是否将角分成相等的两个角即可.
1
点P在∠MAN的内部,现有4个等式;①∠PAM=
∠NAP;②∠PAN=
∠MAN;③∠MAP=
∠MAN;④∠MAN=∠MAP+∠PAN,其中能表
示AP是∠MAN的平分线的有( )
A.1个
B.2个
C.3个
D.4个
知3-练
C
如图所示,若有∠BAD=∠CAD,∠BCE=∠ACE,
则下列结论中错误的是( )
A.AD是∠BAC的平分线
B.CE是∠ACD的平分线
C.∠BCE=
∠ACB
D.CE是∠ABC的平分线
(中考?大连)如图,点O在直线AB上,
射线OC平分∠BOD,若∠COB=
35°,则∠AOD等于( )
A.35° B.70° C.110° D.145°
知3-练
2
3
D
C
这节课你有哪些收获?你觉得还有哪些地方存
在疑问,不妨与同伴交流.
1.必做:
完成教材P120-121
习题T1-T4
第四章
基本平面图形
4.4
角的比较
1
课堂讲解
角的比较
角的和差
角的平分线
2
课时流程
逐点
导讲练
课堂小结
作业提升
问题:有一天学生张虎和王鹏各带了一把折扇(如图),
下面是他们的一段对话:
张:我的折扇大一些,所以我的折扇的角
也大一些.
王:我的折扇长一些,所以我的折扇的角也大一些.
同学们,你们有办法帮他们进行判断吗?
A
B
C
D
E
F
怎样比较∠ABC和∠DEF的大小?
1
知识点
角的比较
知1-导
角的比较:
请同学们任意画出两个角比较一下,并讨论你们的比较方法:
B
A
C
E
D
F
你的方法有:
(1)度量法比较
(2)叠合法比较
知1-讲
一.
度量法
1、对“中”—角的顶点对量角器的中心
3、读数—读出角的另一边所对的度数
2、重合—角的一边与量角器的0°刻度线重合
B
C
A
F
E
D
700
∠ABC
>
∠DEF
30°
知1-讲
A
B
O
1.将两个角的顶点及一边重合
2.两个角的另一边落在重合一边的同侧
3.由两个角的另一边的位置确定两个角的大小
二.
叠合法
C
D
E
∠DCE>∠AOB
知1-讲
O
A
B
D
C
E
A
O
B
C
D
E
∠DCE<∠AOB
∠
DCE
=∠AOB
知1-讲
例1
根据图,回答下列问题:
(1)比较∠FOD与∠FOE的大小;
(2)借助三角尺比较∠DOE
与
∠DOF
的大小.
导引:(1)中两个角有重合边和重合顶点,利用叠合法
比较一目了然,因为OD
边在∠FOE的内部,
所以有∠FOD
<∠FOE.
(2)∠DOE明显大于
45°,而∠DOF
明显小于
45°,故有∠DOE
>∠DOF.
知1-讲
解:(1)∠FOD<∠FOE.
(2)用含有45°角的三角尺比较,可得∠DOE>
45°,∠DOF<45°,所以∠DOE>∠DOF.
总
结
知1-讲
用叠合法比较角的大小时,一定要将两个角的
另一边落在重合边的同侧.两边都不重合,或有一
边重合但另一边在重合边的异侧的两角,可通过度
量法比较大小.
1
在∠AOB的内部任取一点C,作射线OC,那么
有( )
A.∠AOC=∠BOC B.∠AOC>∠BOC
C.∠BOC>∠AOB
D.∠AOB>∠AOC
如图,如果∠AOB=∠COD,那么( )
A.∠1>∠2
B.∠1=∠2
C.∠1<∠2
D.以上都不对
知1-练
2
B
B
知2-讲
2
知识点
角的和差
思考
如图,图中共有几个角?
它们之间有
什么关系?
图中,∠AOC
是∠AOB
与∠BOC
的和,记作
∠AOC=∠AOB
+
∠BOC.
∠AOB
是∠AOC
与∠BOC
的差,记作∠AOB
=
∠AOC
-∠BOC.
类似地,∠AOC
-∠AOB=____________.
∠BOC
例3
如图,∠AOB=48°,∠1=
32°24′,求∠2的度数.
导引:要求∠2的度数,就是要把它转
化为用已知角∠1的关系式来表示.根据图形可
知,∠1+∠2=∠AOB,因此∠2=∠AOB-∠1.
解:因为∠AOB=48°,∠1=32°24′,
所以∠2=48°-32°24′
=47°60′-32°24′=15°36′.
知2-讲
例4
如图,OC是∠AOD的平分线,
OE是∠BOD的平分线.
(1)如果∠AOB=130°,那么
∠COE是多少度?
(2)在(1)的条件下,如果∠DOC
=20°,那么∠BOE是多少度?
导引:(1)由已知可知∠DOC=
∠AOD,∠DOE=
∠BOD.由于∠COE=∠DOC+∠DOE,因此,
∠COE=
∠AOD+
∠BOD=
∠AOB.
(2)结合(1)的结论可求出∠DOE的度数,从而求出
∠BOE的度数.
知2-讲
解:(1)因为OC平分∠AOD,
所以∠DOC=
∠AOD.
因为OE平分∠BOD,
所以∠DOE=
∠BOD.
所以∠COE=∠DOC+∠DOE=
(∠AOD+∠BOD)
∠AOB=
×130°=65°.
(2)由(1)可知∠COE=65°,因为∠DOC=20°,
所以∠DOE=∠COE-∠DOC=45°.
因为OE平分∠BOD,
所以∠BOE=∠DOE=45°.
知2-讲
总
结
知2-讲
(1)利用角平分线进行计算时,要灵活运用角平分
线的几种不同表达方式.
(2)在计算角的大小时,常常要用到等量代换,用
已知角代替与它相等的未知角.
1
如图,∠AOD-∠AOC=( )
A.∠AOC
B.∠BOC
C.∠BOD
D.∠COD
(中考?滨州)借助一副三角尺,你能画出下面哪个
度数的角( )
A.65°
B.75°
C.85°
D.95°
知2-练
2
D
B
(中考?辽宁)如图,已知直线AB,CD相交
于点O,OA平分∠EOC,∠EOC=110°,则
∠BOD的度数是( )
A.25°
B.35°
C.45°
D.55°
知2-练
3
D
3
知识点
角的平分线
知3-导
如图,在透明纸上画一个角,沿着顶点对折,
使角的两边重合.∠AOC被折痕OB分成的两个角有
什么关系?
知3-讲
1.定义:一般地,从一个角的顶点出发,把这个角分
成两个相等的角的射线,叫做这个角的平分线.
要点精析:
(1)角平分线是在角的内部从角的顶点引出的一条射
线,不是直线或线段;
(2)角平分线把角分成了两个相等的角.
知3-讲
例2
如图,∠1=∠2,∠3=∠4,则
下列结论:①AD平分∠BAF;
②AF平分∠DAC;③AE平分
∠DAF;④AF平分∠BAC;
⑤AE平分∠BAC中,正确的有( )
A.4个 B.3个
C.2个
D.1个
导引:由角的平分线的几何表示可知:当∠1=∠2时,
AE平分∠DAF;再由∠3=∠4可得∠1+∠3=
∠2+∠4,即∠BAE=∠CAE,因此AE平分
∠BAC.
C
总
结
知3-讲
判断一条射线是不是角的平分线,只要看这
条射线是否将角分成相等的两个角即可.
1
点P在∠MAN的内部,现有4个等式;①∠PAM=
∠NAP;②∠PAN=
∠MAN;③∠MAP=
∠MAN;④∠MAN=∠MAP+∠PAN,其中能表
示AP是∠MAN的平分线的有( )
A.1个
B.2个
C.3个
D.4个
知3-练
C
如图所示,若有∠BAD=∠CAD,∠BCE=∠ACE,
则下列结论中错误的是( )
A.AD是∠BAC的平分线
B.CE是∠ACD的平分线
C.∠BCE=
∠ACB
D.CE是∠ABC的平分线
(中考?大连)如图,点O在直线AB上,
射线OC平分∠BOD,若∠COB=
35°,则∠AOD等于( )
A.35° B.70° C.110° D.145°
知3-练
2
3
D
C
这节课你有哪些收获?你觉得还有哪些地方存
在疑问,不妨与同伴交流.
1.必做:
完成教材P120-121
习题T1-T4
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
