11.3.1 多边形及其内角和-人教版八年级数学上册【教案】
文档属性
| 名称 | 11.3.1 多边形及其内角和-人教版八年级数学上册【教案】 |
|
|
| 格式 | zip | ||
| 文件大小 | 40.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-12 00:00:00 | ||
图片预览


文档简介
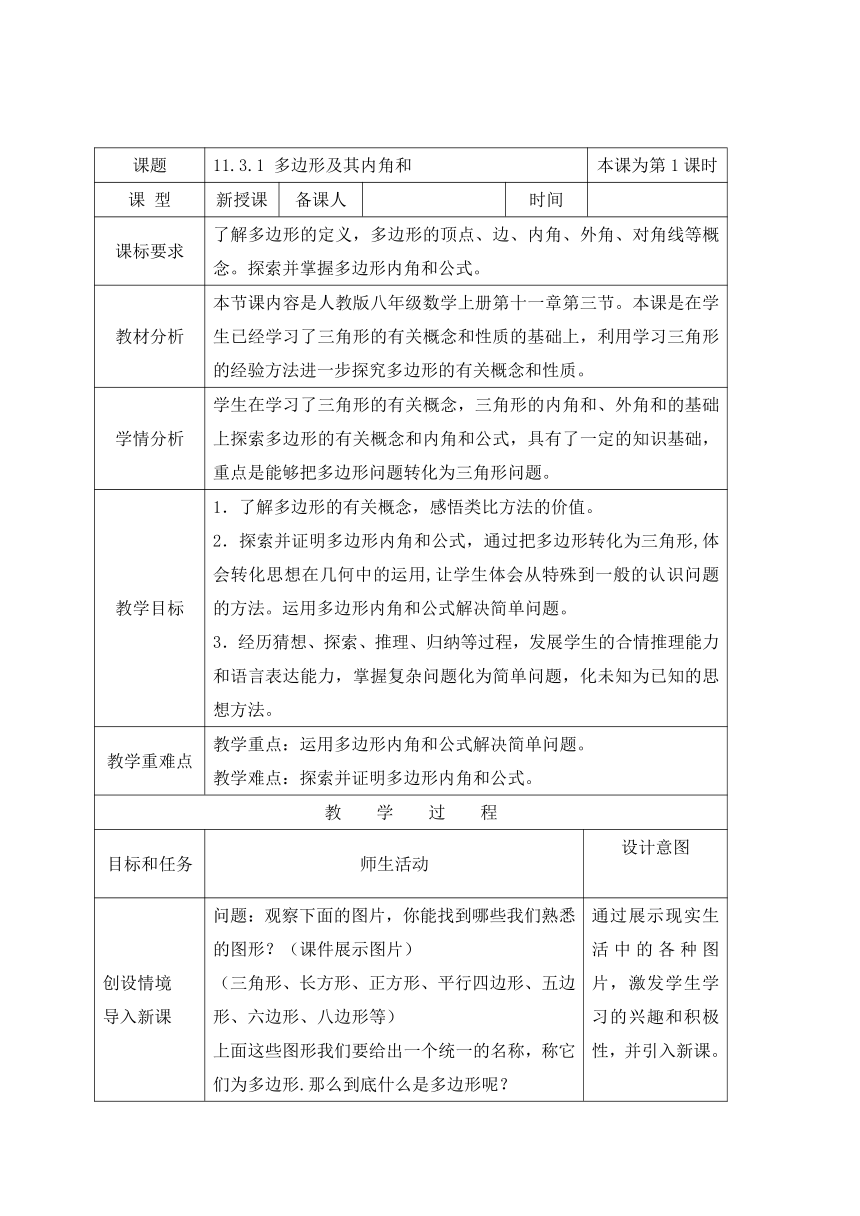
课题
11.3.1
多边形及其内角和
本课为第1课时
课
型
新授课
备课人
时间
课标要求
了解多边形的定义,多边形的顶点、边、内角、外角、对角线等概念。探索并掌握多边形内角和公式。
教材分析
本节课内容是人教版八年级数学上册第十一章第三节。本课是在学生已经学习了三角形的有关概念和性质的基础上,利用学习三角形的经验方法进一步探究多边形的有关概念和性质。
学情分析
学生在学习了三角形的有关概念,三角形的内角和、外角和的基础上探索多边形的有关概念和内角和公式,具有了一定的知识基础,重点是能够把多边形问题转化为三角形问题。
教学目标
1.了解多边形的有关概念,感悟类比方法的价值。2.探索并证明多边形内角和公式,通过把多边形转化为三角形,体会转化思想在几何中的运用,让学生体会从特殊到一般的认识问题的方法。运用多边形内角和公式解决简单问题。3.经历猜想、探索、推理、归纳等过程,发展学生的合情推理能力和语言表达能力,掌握复杂问题化为简单问题,化未知为已知的思想方法。
教学重难点
教学重点:运用多边形内角和公式解决简单问题。教学难点:探索并证明多边形内角和公式。
教学过程
目标和任务
师生活动
设计意图
创设情境导入新课
问题:观察下面的图片,你能找到哪些我们熟悉的图形?(课件展示图片)(三角形、长方形、正方形、平行四边形、五边形、六边形、八边形等)上面这些图形我们要给出一个统一的名称,称它们为多边形.那么到底什么是多边形呢?
通过展示现实生活中的各种图片,激发学生学习的兴趣和积极性,并引入新课。
师生互动探究新知师生互动探究新知
1.观察多边形的构成,类比三角形的有关概念探索多边形的有关概念。问题1:类比三角形的概念,你能说出什么是多边形吗?学生交流,教师讲解并强调“在平面内”,并总结:在平面内,由一些线段首尾顺次相接组成的封闭图形叫多边形。问题2:根据图示,类比三角形的有关概念,说明什么是多边形的边、顶点、内角、外角和对角线。问题3:三角形有对角线吗?为什么?(三角形没有对角线,因为三角形只有三个顶点,而这三个顶点是两两相邻的,它没有不相邻的顶点,所以没有对角线。)问题4:回想三角形的表示方法,多边形应如何表示?学生讨论回答并得出结论。问题5:如图所示,观察两个图形,找出相同点和不同点。学生讨论,教师讲解并给出需要注意的问题。2.正多边形的概念及基本性质(1)各个角都相等,各条边都相等的多边形叫做正多边形。(2)正多边形的性质:正多边形的各个角都相等,各条边都相等。3.探究多边形的内角和回忆 长方形、正方形的内角和等于______。思考 任意一个四边形的内角和也等于360吗?学生思考交流,教师引导。探究(1)从四边形的一个顶点出发,可以作___条对角线,它们将四边形分为
个三角形,四边形的内角和等于180°×____= °(2)如图,从五边形的一个顶点出发,可以作 条对角线,它们将五边形分为____个三角形,五边形的内角和等于
180°×
= °(3)如图,从六边形的一个顶点出发,可以作____条对角线,它们将六边形分为_____个三角形,六边形的内角和等于180°×____=______°思考 你能从四边形、五边形、六边形的内角和的探究过程获得启发,发现多边形的内角和与边数的关系吗?能证明你发现的结论吗?学生讨论,教师引导得出结论:n
边形的内角和等于(n
-2)×180°
类比三角形的有关概念探索多边形的有关概念,感悟类比方法的价值。引导学生通过连接多边形的对角线把多边形问题转化为三角问题,利用三角形内角和定理探索多边形的内角和,体会转化思想在几何中的运用。
运用新知解决问题
例1
填空:(1)十边形的内角和为
度。(2)已知一个多边形的内角和为1
080°,则它的边数为______。例2 如果一个四边形的一组对角互补,那么另一组对角有什么关系?(课本22页例1)
运用多边形内角和公式解决简单问题。
课堂小结
1.本节课学习了哪些主要内容?
2.在探究多边形内角和公式中,连接对角线起什么作用?(转化)
小结本节课的知识点,数学思想方法。
练习与检测
习题11.3
复习巩固
第1、2、4、5题。
板书设计
11.3.1
多边形及其内角和1.多边形2.多边形的对角线3.多边形的内角和公式
(n
-2)×180°
转化
多边形问题
三角形问题
(未知)
(已知)
1、
三级备课:备课实行全册备课、单元备课和课时备课三级备课。
2、
课时备课可用表格形式或者Word形式,但各个环节必须一致。
三、教学反思:课后注重总结积累教学经验,改进教学,要结合校本研修主题进行反思。
注意:教案Word形式排版格式:标题用黑体三号,正文用宋体小四1.5倍行距,汉子一二三后面用“、”,数字123后面用“.”,带括号的数字后面不用标点,需要检查时双面打印。
11.3.1
多边形及其内角和
本课为第1课时
课
型
新授课
备课人
时间
课标要求
了解多边形的定义,多边形的顶点、边、内角、外角、对角线等概念。探索并掌握多边形内角和公式。
教材分析
本节课内容是人教版八年级数学上册第十一章第三节。本课是在学生已经学习了三角形的有关概念和性质的基础上,利用学习三角形的经验方法进一步探究多边形的有关概念和性质。
学情分析
学生在学习了三角形的有关概念,三角形的内角和、外角和的基础上探索多边形的有关概念和内角和公式,具有了一定的知识基础,重点是能够把多边形问题转化为三角形问题。
教学目标
1.了解多边形的有关概念,感悟类比方法的价值。2.探索并证明多边形内角和公式,通过把多边形转化为三角形,体会转化思想在几何中的运用,让学生体会从特殊到一般的认识问题的方法。运用多边形内角和公式解决简单问题。3.经历猜想、探索、推理、归纳等过程,发展学生的合情推理能力和语言表达能力,掌握复杂问题化为简单问题,化未知为已知的思想方法。
教学重难点
教学重点:运用多边形内角和公式解决简单问题。教学难点:探索并证明多边形内角和公式。
教学过程
目标和任务
师生活动
设计意图
创设情境导入新课
问题:观察下面的图片,你能找到哪些我们熟悉的图形?(课件展示图片)(三角形、长方形、正方形、平行四边形、五边形、六边形、八边形等)上面这些图形我们要给出一个统一的名称,称它们为多边形.那么到底什么是多边形呢?
通过展示现实生活中的各种图片,激发学生学习的兴趣和积极性,并引入新课。
师生互动探究新知师生互动探究新知
1.观察多边形的构成,类比三角形的有关概念探索多边形的有关概念。问题1:类比三角形的概念,你能说出什么是多边形吗?学生交流,教师讲解并强调“在平面内”,并总结:在平面内,由一些线段首尾顺次相接组成的封闭图形叫多边形。问题2:根据图示,类比三角形的有关概念,说明什么是多边形的边、顶点、内角、外角和对角线。问题3:三角形有对角线吗?为什么?(三角形没有对角线,因为三角形只有三个顶点,而这三个顶点是两两相邻的,它没有不相邻的顶点,所以没有对角线。)问题4:回想三角形的表示方法,多边形应如何表示?学生讨论回答并得出结论。问题5:如图所示,观察两个图形,找出相同点和不同点。学生讨论,教师讲解并给出需要注意的问题。2.正多边形的概念及基本性质(1)各个角都相等,各条边都相等的多边形叫做正多边形。(2)正多边形的性质:正多边形的各个角都相等,各条边都相等。3.探究多边形的内角和回忆 长方形、正方形的内角和等于______。思考 任意一个四边形的内角和也等于360吗?学生思考交流,教师引导。探究(1)从四边形的一个顶点出发,可以作___条对角线,它们将四边形分为
个三角形,四边形的内角和等于180°×____= °(2)如图,从五边形的一个顶点出发,可以作 条对角线,它们将五边形分为____个三角形,五边形的内角和等于
180°×
= °(3)如图,从六边形的一个顶点出发,可以作____条对角线,它们将六边形分为_____个三角形,六边形的内角和等于180°×____=______°思考 你能从四边形、五边形、六边形的内角和的探究过程获得启发,发现多边形的内角和与边数的关系吗?能证明你发现的结论吗?学生讨论,教师引导得出结论:n
边形的内角和等于(n
-2)×180°
类比三角形的有关概念探索多边形的有关概念,感悟类比方法的价值。引导学生通过连接多边形的对角线把多边形问题转化为三角问题,利用三角形内角和定理探索多边形的内角和,体会转化思想在几何中的运用。
运用新知解决问题
例1
填空:(1)十边形的内角和为
度。(2)已知一个多边形的内角和为1
080°,则它的边数为______。例2 如果一个四边形的一组对角互补,那么另一组对角有什么关系?(课本22页例1)
运用多边形内角和公式解决简单问题。
课堂小结
1.本节课学习了哪些主要内容?
2.在探究多边形内角和公式中,连接对角线起什么作用?(转化)
小结本节课的知识点,数学思想方法。
练习与检测
习题11.3
复习巩固
第1、2、4、5题。
板书设计
11.3.1
多边形及其内角和1.多边形2.多边形的对角线3.多边形的内角和公式
(n
-2)×180°
转化
多边形问题
三角形问题
(未知)
(已知)
1、
三级备课:备课实行全册备课、单元备课和课时备课三级备课。
2、
课时备课可用表格形式或者Word形式,但各个环节必须一致。
三、教学反思:课后注重总结积累教学经验,改进教学,要结合校本研修主题进行反思。
注意:教案Word形式排版格式:标题用黑体三号,正文用宋体小四1.5倍行距,汉子一二三后面用“、”,数字123后面用“.”,带括号的数字后面不用标点,需要检查时双面打印。
