2021-2022学年湘教版数学九年级上册3.4.1 相似三角形的判定课件(共28张)
文档属性
| 名称 | 2021-2022学年湘教版数学九年级上册3.4.1 相似三角形的判定课件(共28张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-12 13:24:31 | ||
图片预览





文档简介
(共28张PPT)
湘教版·
数学·
九年级(上)
3.4.1
相似三角形的判定
第三章
图形的相似
1.经历三角形相似的判定方法“两边对应成比例,且夹角相等的两个三角形相似”的探索过程,积累数学活动的经验。
2.知道两个三角形相似的判定,会利用三角形的相似解决一些简单的实际问题。
学习目标
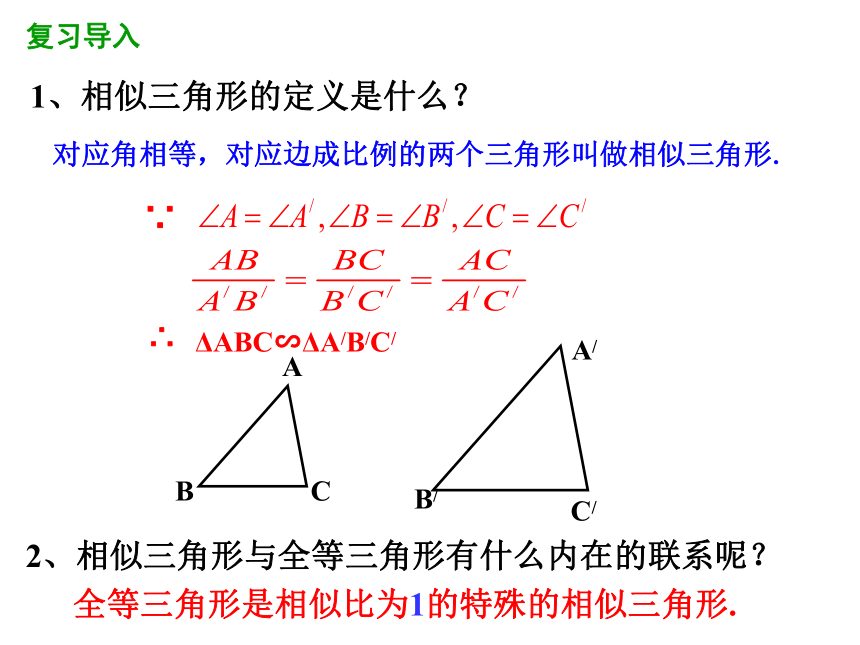
1、相似三角形的定义是什么?
A
C/
B/
A/
C
B
∵
∴
ΔABC∽ΔA/B/C/
2、相似三角形与全等三角形有什么内在的联系呢?
全等三角形是相似比为1的特殊的相似三角形.
对应角相等,对应边成比例的两个三角形叫做相似三角形.
复习导入
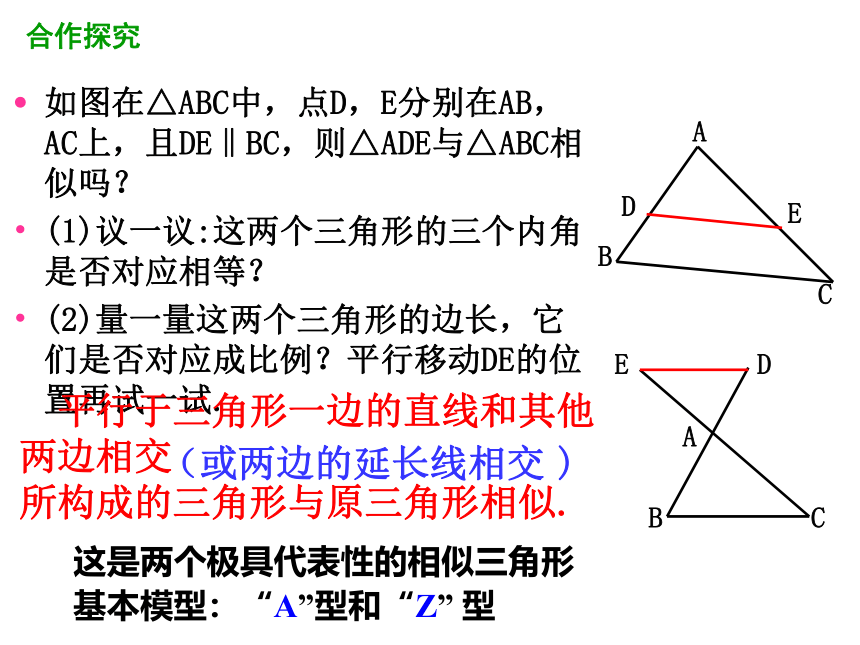
如图在△ABC中,点D,E分别在AB,AC上,且DE‖BC,则△ADE与△ABC相似吗?
(1)议一议:这两个三角形的三个内角是否对应相等?
(2)量一量这两个三角形的边长,它们是否对应成比例?平行移动DE的位置再试一试.
平行于三角形一边的直线和其他两边相交
所构成的三角形与原三角形相似.
D
A
E
C
B
D
A
E
C
B
(或两边的延长线相交
)
这是两个极具代表性的相似三角形
基本模型:“A”型和“Z”
型
合作探究
分析:要证两个三角形相似,
目前只有两个途径:
A
B
C
A/
C/
B/
命题:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
已知:在△ABC
和△A/B/C/
中,
求证:ΔABC∽
△A/B/C/
(把小的三角形移动到大的三角形上).
怎样实现移动呢?
(1)三角形相似的定义;(显然条件不具备)
(2)本节课开始学习的利用平行线来判定三角形相似的定理.
为了使用它,就必须创造具备定理的基本图形的条件.怎样创造呢?
证明:在ΔABC的边AB、AC上,分别截取AD=A/B/,AE=A/C/,连结DE.
A
B
C
A/
C/
B/
D
E
∵
AD=A/B/,∠A=∠A/,AE=A/C/
∴
ΔA
DE≌ΔA/B/C/,
∴
∠ADE=∠B/,
又∵
∠B/=∠B,
∴
∠ADE=∠B,
∴
DE//BC,
∴
ΔADE∽ΔABC.
∴
ΔA/B/C/∽ΔABC
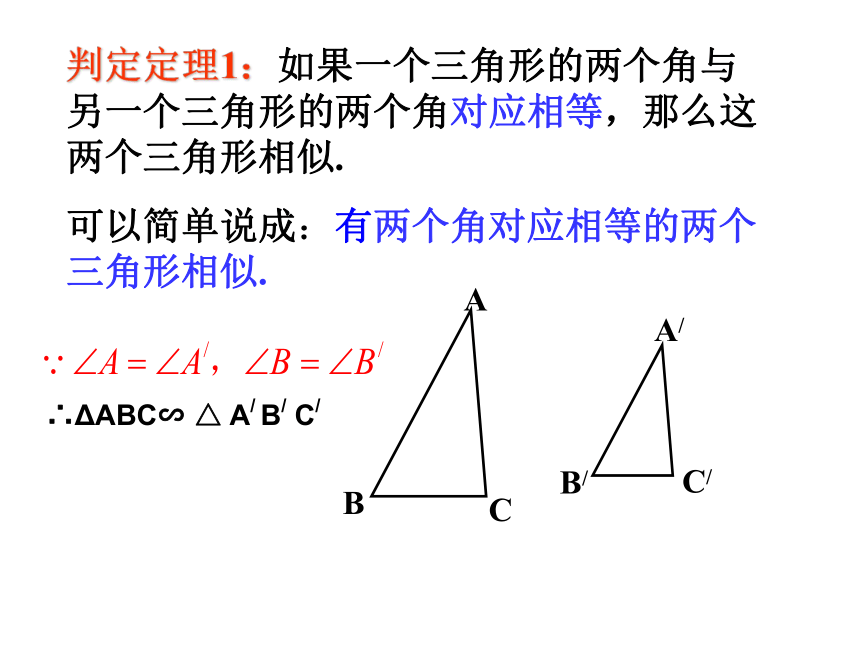
判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
可以简单说成:有两个角对应相等的两个
三角形相似.
A
B
C
A/
C/
B/
∴ΔABC∽
△
A/
B/
C/
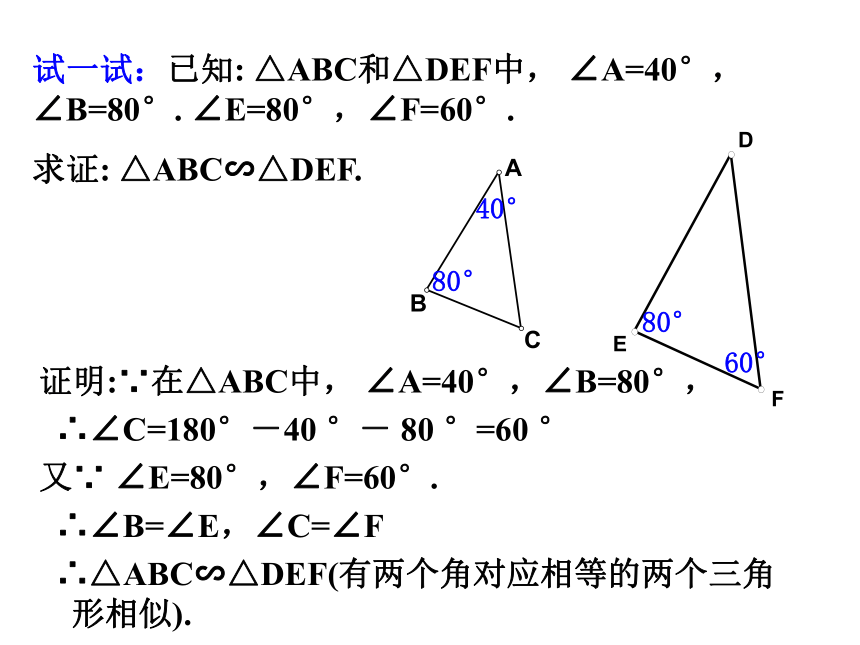
证明:∵在△ABC中,
∠A=40°,∠B=80°,
∴∠C=180°-40
°-
80
°=60
°
又∵
∠E=80°,∠F=60°.
∴∠B=∠E,∠C=∠F
∴△ABC∽△DEF(有两个角对应相等的两个三角形相似).
试一试:已知:
△ABC和△DEF中,
∠A=40°,∠B=80°.
∠E=80°,∠F=60°.
求证:
△ABC∽△DEF.
A
B
C
40°
80°
80°
60°
1.已知等腰三角形ΔABC和ΔA/B/C/中,∠A、∠A/分别是顶角,求证:
①如果∠A=∠A/,那么ΔABC∽ΔA/B/C/.
②如果∠B=∠B/,那么ΔABC∽ΔA/B/C/.
A
B
C
A/
B/
C/
A
B
C
A/
B/
C/
课堂练习
2.下列结论中,不正确的是( )
A、有一个角为90°的两个等腰三角形相似
B、有一个角为60°的两个等腰三角形相似
C、有一个角为30°的两个等腰三角形相似
D、有一个角为100°的两个等腰三角形相似
C
小杰采用了如下方法:从A处沿与AB垂直的直线方向走40m到达C处,插一根标杆,然后沿同方向继续走15m到达D处,再右转90度走到E处,使B,C,E三点恰好在一条直线上,量得DE=20m,这样就可以求出河宽AB.请你算出结果(要求给出解题过程)
3.在一次数学活动课上,要测量河宽AB,你有什么方法?
A
B
D
C
E
B
A
4.如图,在ΔABC中
,点D、E分别是边AB、AC上的点,连结DE,利用所学的知识讨论:当具备怎样的条件时,ΔADE与
ΔABC相似?
A
B
C
D
E
A
B
C
D
E
1.平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
3.相似三角形判定定理的应用.
2.
判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
简单说成:有两个角对应相等的两个三角形相似.
归纳新知
1.如图,已知BC交AD于点E,AB∥EF∥CD,那么图中相似的三角形共有(
)
A.1对
B.2对
C.3对
D.4对
C
课后练习
2.如图,在△ABC中,D,E分别是AB,AC的中点,则△ADE∽__________.
△ABC
3.如图,AB∥CD,AC,BD,EF相交于点O,则图中相似三角形共有____对;分别是___________________________________________.
3
△AOB∽△COD;△AOE∽△COF;△BOE∽△DOF
4.如图,BE是△ABC的角平分线,延长BE至点D,使得BC=CD.求证:△AEB∽△CED.
证明:∵BE是△ABC的角平分线,∴∠ABE=∠CBD.∵BC=CD,∴∠D=∠CBD=∠ABE.∴AB∥CD,∴△AEB∽△CED
5.(2019·贺州)如图,在△ABC中,D,E分别是AB,AC边上的点,DE∥BC,若AD=2,AB=3,DE=4,则BC等于(
)
A.5
B.6
C.7
D.8
B
6.(2019·重庆)如图,△ABO∽△CDO,若BO=6,DO=3,CD=2,则AB的长是(
)
A.2
B.3
C.4
D.5
C
7.如图,在梯形ABCD中,AB∥CD,AC与BD交于O,OA∶OC=1∶2,AB=3,则CD=____.
6
8.如图,在△ABC中,点D,E,F,G分别是边AB,AC的三等分点,则DF∶EG∶BC=______________.
1∶2∶3
9.(例2变式)如图:在平行四边形ABCD中,E是AB延长线上点,DE交BC于点F.
(1)求证:△DFC∽△EFB;
(2)若DC=6,BE=4,DE=10,求DF的长度?
(1)证明:∵在平行四边形ABCD中,∴AE∥CD,∴△DFC∽△EFB
C
11.(2019·玉林)如图,AB∥EF∥DC,AD∥BC,EF与AC交于点G,则是相似三角形共有(
)
A.3对
B.5对
C.6对
D.8对
C
12.如图,在四边形ABCD中,AD∥BC∥EF,EF分别与AB,AC,CD相交于点E,M,F,若EM∶BC=2∶5,CD=5,则FC=____.
3
14.如图,在△ABC中,D在AB上,DE∥BC交AC于点E,EF∥AB交BC于F,求证:△ADE∽△EFC.
证明:∵DE∥BC,EF∥AB,∴△ADE∽△ABC,△EFC∽△ABC,∴△ADE∽△EFC
15.如图,在Rt△ABC中,∠C=90°,AC=12,AB=13,正方形CEDF按如图所示的方式放置,求正方形的边长.
湘教版·
数学·
九年级(上)
3.4.1
相似三角形的判定
第三章
图形的相似
1.经历三角形相似的判定方法“两边对应成比例,且夹角相等的两个三角形相似”的探索过程,积累数学活动的经验。
2.知道两个三角形相似的判定,会利用三角形的相似解决一些简单的实际问题。
学习目标
1、相似三角形的定义是什么?
A
C/
B/
A/
C
B
∵
∴
ΔABC∽ΔA/B/C/
2、相似三角形与全等三角形有什么内在的联系呢?
全等三角形是相似比为1的特殊的相似三角形.
对应角相等,对应边成比例的两个三角形叫做相似三角形.
复习导入
如图在△ABC中,点D,E分别在AB,AC上,且DE‖BC,则△ADE与△ABC相似吗?
(1)议一议:这两个三角形的三个内角是否对应相等?
(2)量一量这两个三角形的边长,它们是否对应成比例?平行移动DE的位置再试一试.
平行于三角形一边的直线和其他两边相交
所构成的三角形与原三角形相似.
D
A
E
C
B
D
A
E
C
B
(或两边的延长线相交
)
这是两个极具代表性的相似三角形
基本模型:“A”型和“Z”
型
合作探究
分析:要证两个三角形相似,
目前只有两个途径:
A
B
C
A/
C/
B/
命题:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
已知:在△ABC
和△A/B/C/
中,
求证:ΔABC∽
△A/B/C/
(把小的三角形移动到大的三角形上).
怎样实现移动呢?
(1)三角形相似的定义;(显然条件不具备)
(2)本节课开始学习的利用平行线来判定三角形相似的定理.
为了使用它,就必须创造具备定理的基本图形的条件.怎样创造呢?
证明:在ΔABC的边AB、AC上,分别截取AD=A/B/,AE=A/C/,连结DE.
A
B
C
A/
C/
B/
D
E
∵
AD=A/B/,∠A=∠A/,AE=A/C/
∴
ΔA
DE≌ΔA/B/C/,
∴
∠ADE=∠B/,
又∵
∠B/=∠B,
∴
∠ADE=∠B,
∴
DE//BC,
∴
ΔADE∽ΔABC.
∴
ΔA/B/C/∽ΔABC
判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
可以简单说成:有两个角对应相等的两个
三角形相似.
A
B
C
A/
C/
B/
∴ΔABC∽
△
A/
B/
C/
证明:∵在△ABC中,
∠A=40°,∠B=80°,
∴∠C=180°-40
°-
80
°=60
°
又∵
∠E=80°,∠F=60°.
∴∠B=∠E,∠C=∠F
∴△ABC∽△DEF(有两个角对应相等的两个三角形相似).
试一试:已知:
△ABC和△DEF中,
∠A=40°,∠B=80°.
∠E=80°,∠F=60°.
求证:
△ABC∽△DEF.
A
B
C
40°
80°
80°
60°
1.已知等腰三角形ΔABC和ΔA/B/C/中,∠A、∠A/分别是顶角,求证:
①如果∠A=∠A/,那么ΔABC∽ΔA/B/C/.
②如果∠B=∠B/,那么ΔABC∽ΔA/B/C/.
A
B
C
A/
B/
C/
A
B
C
A/
B/
C/
课堂练习
2.下列结论中,不正确的是( )
A、有一个角为90°的两个等腰三角形相似
B、有一个角为60°的两个等腰三角形相似
C、有一个角为30°的两个等腰三角形相似
D、有一个角为100°的两个等腰三角形相似
C
小杰采用了如下方法:从A处沿与AB垂直的直线方向走40m到达C处,插一根标杆,然后沿同方向继续走15m到达D处,再右转90度走到E处,使B,C,E三点恰好在一条直线上,量得DE=20m,这样就可以求出河宽AB.请你算出结果(要求给出解题过程)
3.在一次数学活动课上,要测量河宽AB,你有什么方法?
A
B
D
C
E
B
A
4.如图,在ΔABC中
,点D、E分别是边AB、AC上的点,连结DE,利用所学的知识讨论:当具备怎样的条件时,ΔADE与
ΔABC相似?
A
B
C
D
E
A
B
C
D
E
1.平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
3.相似三角形判定定理的应用.
2.
判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
简单说成:有两个角对应相等的两个三角形相似.
归纳新知
1.如图,已知BC交AD于点E,AB∥EF∥CD,那么图中相似的三角形共有(
)
A.1对
B.2对
C.3对
D.4对
C
课后练习
2.如图,在△ABC中,D,E分别是AB,AC的中点,则△ADE∽__________.
△ABC
3.如图,AB∥CD,AC,BD,EF相交于点O,则图中相似三角形共有____对;分别是___________________________________________.
3
△AOB∽△COD;△AOE∽△COF;△BOE∽△DOF
4.如图,BE是△ABC的角平分线,延长BE至点D,使得BC=CD.求证:△AEB∽△CED.
证明:∵BE是△ABC的角平分线,∴∠ABE=∠CBD.∵BC=CD,∴∠D=∠CBD=∠ABE.∴AB∥CD,∴△AEB∽△CED
5.(2019·贺州)如图,在△ABC中,D,E分别是AB,AC边上的点,DE∥BC,若AD=2,AB=3,DE=4,则BC等于(
)
A.5
B.6
C.7
D.8
B
6.(2019·重庆)如图,△ABO∽△CDO,若BO=6,DO=3,CD=2,则AB的长是(
)
A.2
B.3
C.4
D.5
C
7.如图,在梯形ABCD中,AB∥CD,AC与BD交于O,OA∶OC=1∶2,AB=3,则CD=____.
6
8.如图,在△ABC中,点D,E,F,G分别是边AB,AC的三等分点,则DF∶EG∶BC=______________.
1∶2∶3
9.(例2变式)如图:在平行四边形ABCD中,E是AB延长线上点,DE交BC于点F.
(1)求证:△DFC∽△EFB;
(2)若DC=6,BE=4,DE=10,求DF的长度?
(1)证明:∵在平行四边形ABCD中,∴AE∥CD,∴△DFC∽△EFB
C
11.(2019·玉林)如图,AB∥EF∥DC,AD∥BC,EF与AC交于点G,则是相似三角形共有(
)
A.3对
B.5对
C.6对
D.8对
C
12.如图,在四边形ABCD中,AD∥BC∥EF,EF分别与AB,AC,CD相交于点E,M,F,若EM∶BC=2∶5,CD=5,则FC=____.
3
14.如图,在△ABC中,D在AB上,DE∥BC交AC于点E,EF∥AB交BC于F,求证:△ADE∽△EFC.
证明:∵DE∥BC,EF∥AB,∴△ADE∽△ABC,△EFC∽△ABC,∴△ADE∽△EFC
15.如图,在Rt△ABC中,∠C=90°,AC=12,AB=13,正方形CEDF按如图所示的方式放置,求正方形的边长.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
