2021-2022学年 九年级数学湘教版上册3.2 平行线分线段成比例课件(共34张)
文档属性
| 名称 | 2021-2022学年 九年级数学湘教版上册3.2 平行线分线段成比例课件(共34张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-12 13:25:16 | ||
图片预览





文档简介
(共34张PPT)
湘教版·
数学·
九年级(上)
3.2
平行线分线段成比例
第三章
图形的相似
掌握平行线分线段成比例定理和三角形一边的平行线的性质定理,并会灵活运用。
学习目标
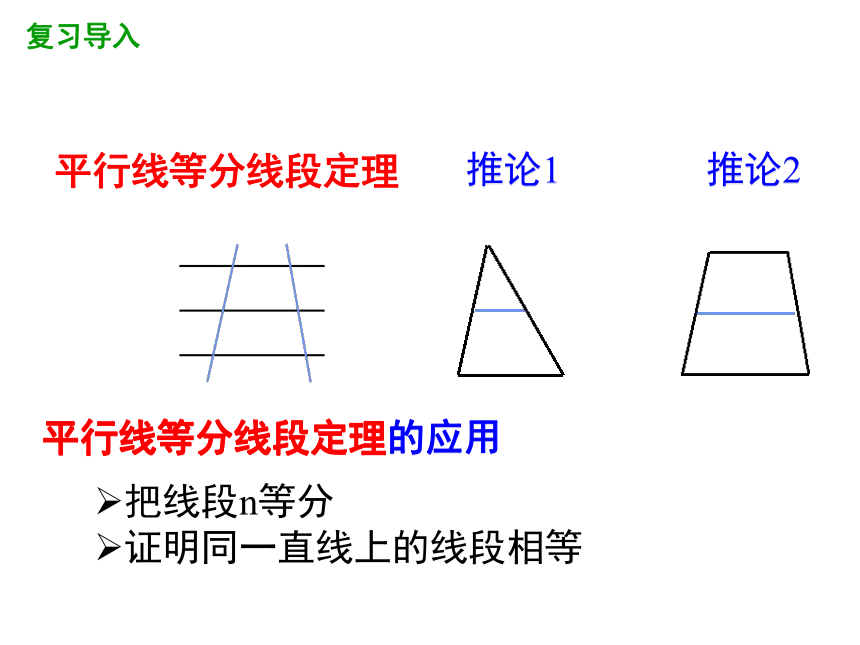
平行线等分线段定理
推论1
推论2
平行线等分线段定理的应用
把线段n等分
证明同一直线上的线段相等
推论1
推论2
平行线等分线段定理的应用
复习导入
如何不通过测量,运用所学知识,快速将一条长5厘米的细线分成两部分,使这两部分之比是2:3?
A
B
C
合作探究
平行线等分线段定理的条件
相邻的两条平行线间的距离相等
一组平行线中相邻两条平行
线间距离不相等,结论如何?
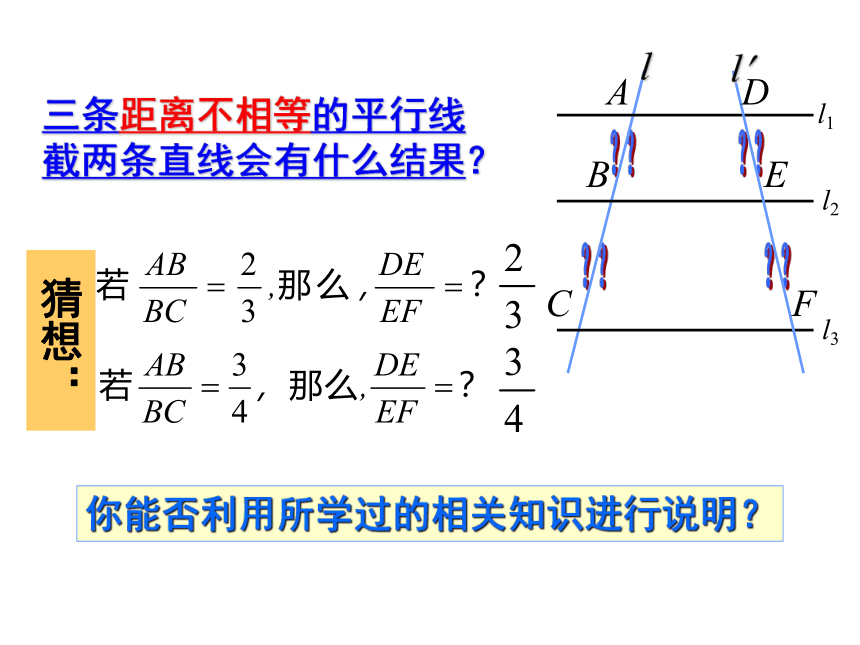
三条距离不相等的平行线截两条直线会有什么结果?
?
?
?
?
猜想:
你能否利用所学过的相关知识进行说明?
A
B
C
D
E
F
l1
l2
l3
l
l?
A
B
C
D
E
F
l1
l2
l3
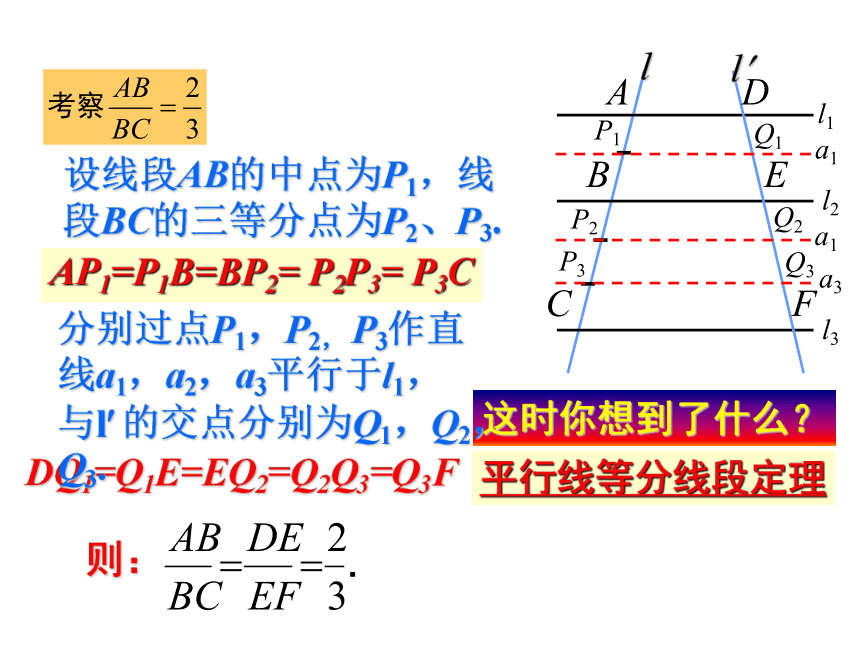
设线段AB的中点为P1,线段BC的三等分点为P2、P3.
P1
P2
P3
Q1
Q2
Q3
a1
a1
a3
则:
这时你想到了什么?
AP1=P1B=BP2=
P2P3=
P3C
DQ1=Q1E=EQ2=Q2Q3=Q3F
平行线等分线段定理
分别过点P1,P2,
P3作直线a1,a2,a3平行于l1,与l?
的交点分别为Q1,Q2,Q3.
l
l?
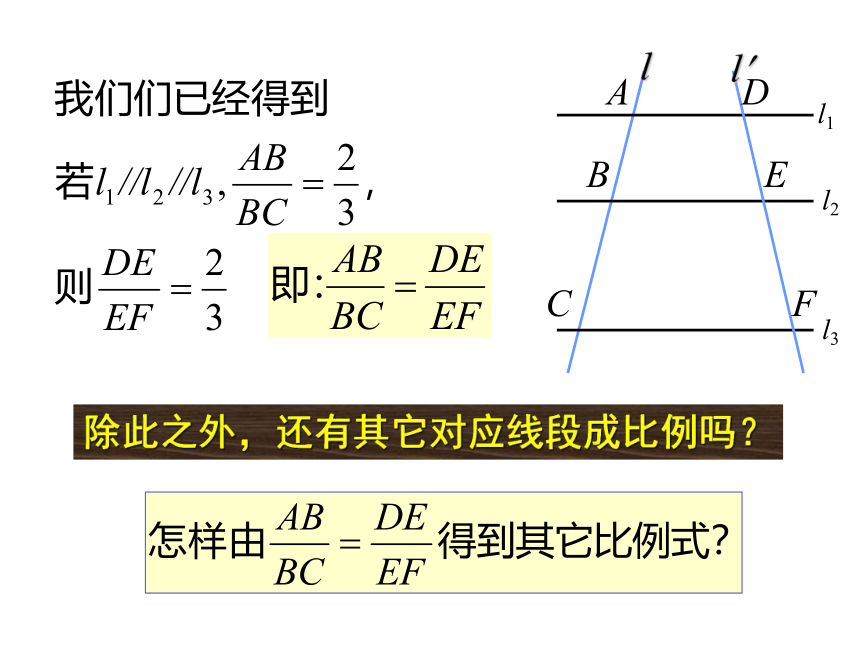
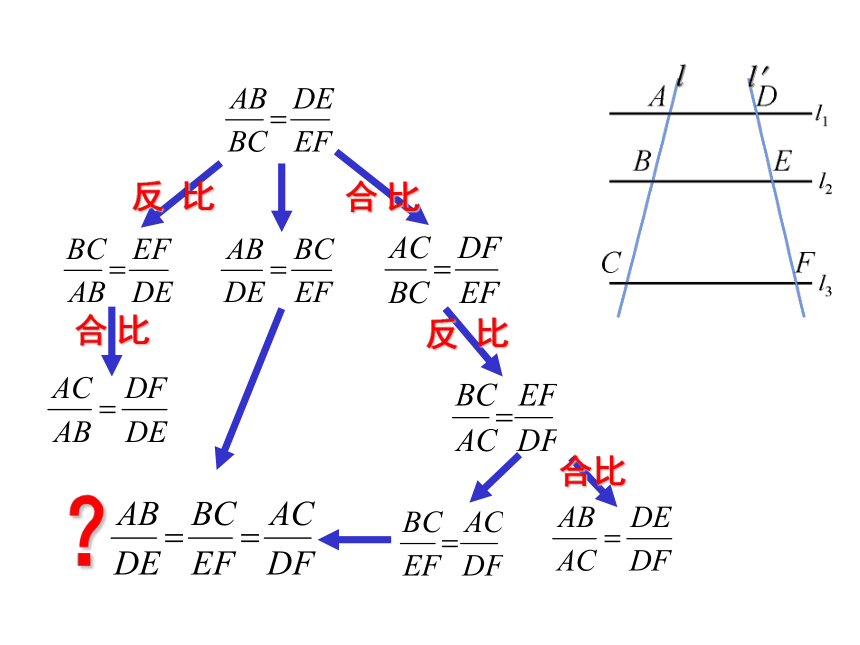
除此之外,还有其它对应线段成比例吗?
A
B
C
D
E
F
l1
l2
l3
l
l?
?
反
比
合
比
合
比
反
比
合比
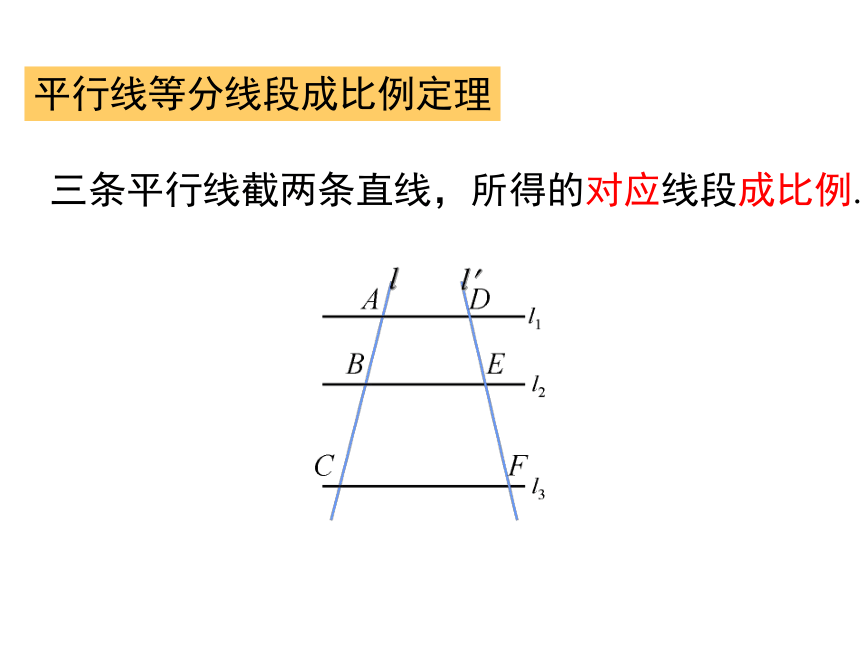
平行线等分线段成比例定理
三条平行线截两条直线,所得的对应线段成比例.
l2
l3
l1
l3
l
l?
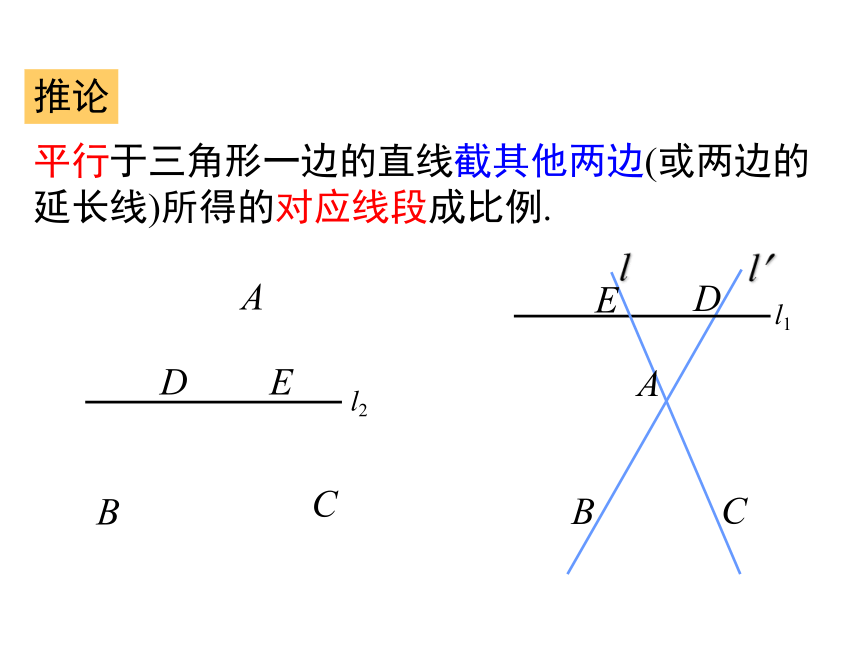
推论
平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.
A
B
C
D
E
l2
A
B
C
D
E
l1
l
l?
平行线分线段成比例定理与平行线等分线段定理有何联系?
A
B
C
D
E
F
A
B
C
D
E
F
结论:后者是前者的一种特殊情况!
例
如图,△ABC中,DE//BC,DF//AC,AE=4,EC=2,
BC=8.求BF和CF的长.
F
A
C
B
分析:运用平行线分线段成比例定理的推论分别列出比例式求解.
解
∵DE//BC
∵DF//AC
D
E
例
如图,△ABC中,DE//BC,EF//CD.
求证:AD是AB和AF的比例中项.
F
E
B
A
C
D
分析:
分别在△ABC及△ADC中利用平行线分线段成比例定理的推论
证明
∴AD2=AB?AF,即AD是AB和AF的比例中项
如图,有一块形状为直角梯形的草地,周围均为水泥直道,两个拐角A、B处均为直角,草地中间另有一条水泥直道EF垂直于AB,垂足为E.已知AE长a米,EB长b米,DF长c米.求CF.
A
B
C
D
a
b
c
?
E
F
用平行于三角形一边且和其他两边相交的直线截三角形,所截得的三角形的三边与原三角形的三边对应成比例.
F
E
B
A
C
D
已知:如图,DE//BC,DE分别交AB、AC于点D、E
DE//BC
EF//AB
DE=BF
如图,直线l1,l2被三个平行平面?,?,?所截,直线l1与它们的交点分别为A,B,C,直线l2分别为D,E,F
探究
一、平行线分线段成比例定理:
三条平行线截两条直线,所得的对应线段成比例.
(关键要能熟练地找出对应线段)
二、要熟悉该定理的几种基本图形
A
B
C
D
E
F
A
B
C
D
E
F
归纳新知
三、注意该定理在三角形中的应用
1.如图,已知AB∥CD∥EF,AD=DF,那么与CE相等的线段为(
)
A.DF
B.AB
C.BC
D.EF
C
课后练习
A
3.如图,AB∥EM∥DC,AE=ED,EF∥BC,EF=12
cm,则BC=____cm.
24
C
5.(2019·淮安)如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于点A,B,C和点D,E,F.若AB=3,DE=2,BC=6,则EF=____.
4
6.如图,已知直线l1,l2,l3分别截直线l4于点A,B,C,截直线l5于点D,E,F,且l1∥l2∥l3.
(1)如果AB=4,BC=8,EF=12,求DE的长;
(2)如果DE∶EF=2∶3,AB=6,求AC的长.
B
8.(2019·内江)如图,在△ABC中,DE∥BC,AD=9,DB=3,CE=2,则AC=____.
8
9.如图,DE∥BC,EF∥CG,AD∶AB=1∶3,AE=3.
(1)求EC的值;
(2)求证:AD·AG=AF·AB.
C
11.如图,直线a∥b,AF∶FB=3∶5,BC∶CD=3∶1,则AE∶EC为(
)
A.5∶12
B.9∶5
C.12∶5
D.3∶2
C
14.如图,直线l1∥l2∥l3,AC分别交l1,l2,l3于点A,B,C;DF分别交l1,l2,l3于点D,E,F;AC与DF交于点O.已知DE=3,EF=6,AB=4.
(1)求AC的长;
(2)若BE∶CF=1∶3,求OB∶AB.
湘教版·
数学·
九年级(上)
3.2
平行线分线段成比例
第三章
图形的相似
掌握平行线分线段成比例定理和三角形一边的平行线的性质定理,并会灵活运用。
学习目标
平行线等分线段定理
推论1
推论2
平行线等分线段定理的应用
把线段n等分
证明同一直线上的线段相等
推论1
推论2
平行线等分线段定理的应用
复习导入
如何不通过测量,运用所学知识,快速将一条长5厘米的细线分成两部分,使这两部分之比是2:3?
A
B
C
合作探究
平行线等分线段定理的条件
相邻的两条平行线间的距离相等
一组平行线中相邻两条平行
线间距离不相等,结论如何?
三条距离不相等的平行线截两条直线会有什么结果?
?
?
?
?
猜想:
你能否利用所学过的相关知识进行说明?
A
B
C
D
E
F
l1
l2
l3
l
l?
A
B
C
D
E
F
l1
l2
l3
设线段AB的中点为P1,线段BC的三等分点为P2、P3.
P1
P2
P3
Q1
Q2
Q3
a1
a1
a3
则:
这时你想到了什么?
AP1=P1B=BP2=
P2P3=
P3C
DQ1=Q1E=EQ2=Q2Q3=Q3F
平行线等分线段定理
分别过点P1,P2,
P3作直线a1,a2,a3平行于l1,与l?
的交点分别为Q1,Q2,Q3.
l
l?
除此之外,还有其它对应线段成比例吗?
A
B
C
D
E
F
l1
l2
l3
l
l?
?
反
比
合
比
合
比
反
比
合比
平行线等分线段成比例定理
三条平行线截两条直线,所得的对应线段成比例.
l2
l3
l1
l3
l
l?
推论
平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.
A
B
C
D
E
l2
A
B
C
D
E
l1
l
l?
平行线分线段成比例定理与平行线等分线段定理有何联系?
A
B
C
D
E
F
A
B
C
D
E
F
结论:后者是前者的一种特殊情况!
例
如图,△ABC中,DE//BC,DF//AC,AE=4,EC=2,
BC=8.求BF和CF的长.
F
A
C
B
分析:运用平行线分线段成比例定理的推论分别列出比例式求解.
解
∵DE//BC
∵DF//AC
D
E
例
如图,△ABC中,DE//BC,EF//CD.
求证:AD是AB和AF的比例中项.
F
E
B
A
C
D
分析:
分别在△ABC及△ADC中利用平行线分线段成比例定理的推论
证明
∴AD2=AB?AF,即AD是AB和AF的比例中项
如图,有一块形状为直角梯形的草地,周围均为水泥直道,两个拐角A、B处均为直角,草地中间另有一条水泥直道EF垂直于AB,垂足为E.已知AE长a米,EB长b米,DF长c米.求CF.
A
B
C
D
a
b
c
?
E
F
用平行于三角形一边且和其他两边相交的直线截三角形,所截得的三角形的三边与原三角形的三边对应成比例.
F
E
B
A
C
D
已知:如图,DE//BC,DE分别交AB、AC于点D、E
DE//BC
EF//AB
DE=BF
如图,直线l1,l2被三个平行平面?,?,?所截,直线l1与它们的交点分别为A,B,C,直线l2分别为D,E,F
探究
一、平行线分线段成比例定理:
三条平行线截两条直线,所得的对应线段成比例.
(关键要能熟练地找出对应线段)
二、要熟悉该定理的几种基本图形
A
B
C
D
E
F
A
B
C
D
E
F
归纳新知
三、注意该定理在三角形中的应用
1.如图,已知AB∥CD∥EF,AD=DF,那么与CE相等的线段为(
)
A.DF
B.AB
C.BC
D.EF
C
课后练习
A
3.如图,AB∥EM∥DC,AE=ED,EF∥BC,EF=12
cm,则BC=____cm.
24
C
5.(2019·淮安)如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于点A,B,C和点D,E,F.若AB=3,DE=2,BC=6,则EF=____.
4
6.如图,已知直线l1,l2,l3分别截直线l4于点A,B,C,截直线l5于点D,E,F,且l1∥l2∥l3.
(1)如果AB=4,BC=8,EF=12,求DE的长;
(2)如果DE∶EF=2∶3,AB=6,求AC的长.
B
8.(2019·内江)如图,在△ABC中,DE∥BC,AD=9,DB=3,CE=2,则AC=____.
8
9.如图,DE∥BC,EF∥CG,AD∶AB=1∶3,AE=3.
(1)求EC的值;
(2)求证:AD·AG=AF·AB.
C
11.如图,直线a∥b,AF∶FB=3∶5,BC∶CD=3∶1,则AE∶EC为(
)
A.5∶12
B.9∶5
C.12∶5
D.3∶2
C
14.如图,直线l1∥l2∥l3,AC分别交l1,l2,l3于点A,B,C;DF分别交l1,l2,l3于点D,E,F;AC与DF交于点O.已知DE=3,EF=6,AB=4.
(1)求AC的长;
(2)若BE∶CF=1∶3,求OB∶AB.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
