湘教八上数学1.4.2分式的通分课件(23张)
文档属性
| 名称 | 湘教八上数学1.4.2分式的通分课件(23张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 22:07:54 | ||
图片预览







文档简介
(共23张PPT)
第4节
分式的加法和减法
第2课时
分式的通分
第1章
分式
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
最简公分母
通分
课时导入
复习提问
引出问题
复习提问
引出问题
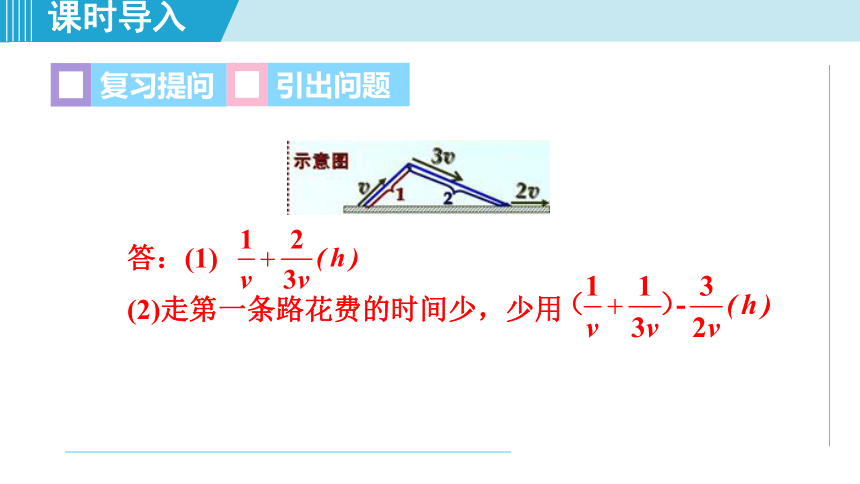
从甲地到乙地有两条路,每一个条路都是3km.其中第一条是平路,第二条有1km的上坡路,2km的下坡路小明在上坡路上的骑车速度为2vkm/h,在平路上的骑车速度为20km/h,在下坡路上的骑车速度为3vkmh,那么:
(1)当走第二条路时,他从甲地到乙地需要
多长时间?
(2)他走哪条路花费时间少?少多长时间?
课时导入
复习提问
引出问题
答:(1)
(2)走第一条路花费的时间少,少用
知识点
最简公分母
知1-导
感悟新知
1
通分时,关键是确定公分母,一般取各分母的所有因式的最高次幂的积作为公分母,这样的公分母称为最简公分母.
知1-讲
感悟新知
确定最简公分母的一般方法:
(1)如果各分母是单项式,那么最简公分母就是由
①各系数的最小公倍数;②相同字母的最高次赛;
③所有不同字母及其指数的乘积这三部分组成;
(2)如果各分母中有多项式,就先把分母是多项式的分解因式,再按照分母是单项式时求最简公分母的方法,从系数、相同因式、不同因式三个方面去确定.
知1-讲
感悟新知
例
1
解析:因为分母分别是(x-1)?、(1-x)3、x-1,所以它们的最简公分母是(x-1)3,故答案选B.
分式
的最简公分母为(
)
A.(x-1)2
B.
(x-1)3
C.
(x-1)
D.
(x-1)2
(1-x)3
B
知1-讲
总
结
感悟新知
如果各分母都是多项式,确定最简公分母的方法:就要把它们分解因式,然后把每个因式当做一个因数(或一个字母),再按照单项式求最简公分母的方法,从系数、相同因式、不同因式三个方面去求.
知1-练
感悟新知
C
B
知2-导
感悟新知
知识点
通分
2
1.下面再来复习分数的加减运算:
知2-导
感悟新知
2.类比分数的加减运算,下面分式的加减运算如何进行?
知2-导
感悟新知
根据分式的基本性质,把几个异分母的分式化成同分母的分式的过程,叫作分式的通分(reduction
of
fractions
to
a
common
denominator).
知2-讲
感悟新知
分式的通分:化异分母分式为同分母分式的过程叫做分式的通分
知2-讲
感悟新知
要点精析:(1)通分的依据是分式的基本性质.
(2)通分的关键是确定几个分式的最简公分母;
(3)分式→约分;分式→通分.
即:
同乘
同除
约分
通分
知2-讲
感悟新知
例2
通分:
解:(1)最简公分母是12xy2,
知2-讲
感悟新知
(2)最简公分母是a2b2c2,
知2-讲
感悟新知
总
结
确定分母是单项式的分式的最简公分母的方法是:①系数取各分母系数的最小公倍数:②同底数幂取次数最高的作为最简公分母的一个因式;③单独出现的字母连同它的指数作为最简公分母的一个因式.
知2-讲
感悟新知
通分:
例
3
分析:(1)中的分母分别是x,x2-x=x(x-1),因此最简公分母是x(x-1)
(2)中的分母因式分解后,分别是x2-4-(x+2)(x-2),4-2x=-2(x-2),因此最简公分母是2(x+2)(x-2).
知2-讲
感悟新知
解:(1)最简公分母是x(x-1),
(2)最简公分母是2(x+2)(x-2),
知2-讲
感悟新知
总
结
分母是多项式的分式的最简公分母的确定方法:(1)将各个分母因式分解;(2)找出每个出现的因式的最高次幂,它们的积为最简公分母的因式;(3)若有系数,则所有系数的最小公倍数是最简公分母的系数.
课堂小结
分式的通分
(1)分式通分的依据是分式的基本性质.
(2)分式通分的关键是确定几个分式的最简公分母.各分母所有因式的最高次幂的积,叫做最简公分母.最简公分母的组成:凡出现字母(或含字母的式子)为底数的幂的因式,选取指数最大的;当各分母的系数为整数时,取它们系数的最小公倍数做最简公分母的系数;当分母为多项式时,一般应先分解因式.公因式与最简分母的区别:公因式是各项系数的最大公约数与相同因式最低次幂的积,而最简公分母是各分母系数的最小公倍数与所有各个因式最高次幂的积.
课堂小结
(3)
确定最简公分母的一般步骤:①取各分母系数的最小公倍;②凡是在分母中出现的字母为底的幂的因式都要取;③以相同字母为底的幂的因式取指数最大的.当各分母是多项式时,先把各多项式分解因式,再按上面的方法求出各分母的最简公分母.
分式的通分
必做:
请完成教材课后习题
课后作业
作业
第4节
分式的加法和减法
第2课时
分式的通分
第1章
分式
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
最简公分母
通分
课时导入
复习提问
引出问题
复习提问
引出问题
从甲地到乙地有两条路,每一个条路都是3km.其中第一条是平路,第二条有1km的上坡路,2km的下坡路小明在上坡路上的骑车速度为2vkm/h,在平路上的骑车速度为20km/h,在下坡路上的骑车速度为3vkmh,那么:
(1)当走第二条路时,他从甲地到乙地需要
多长时间?
(2)他走哪条路花费时间少?少多长时间?
课时导入
复习提问
引出问题
答:(1)
(2)走第一条路花费的时间少,少用
知识点
最简公分母
知1-导
感悟新知
1
通分时,关键是确定公分母,一般取各分母的所有因式的最高次幂的积作为公分母,这样的公分母称为最简公分母.
知1-讲
感悟新知
确定最简公分母的一般方法:
(1)如果各分母是单项式,那么最简公分母就是由
①各系数的最小公倍数;②相同字母的最高次赛;
③所有不同字母及其指数的乘积这三部分组成;
(2)如果各分母中有多项式,就先把分母是多项式的分解因式,再按照分母是单项式时求最简公分母的方法,从系数、相同因式、不同因式三个方面去确定.
知1-讲
感悟新知
例
1
解析:因为分母分别是(x-1)?、(1-x)3、x-1,所以它们的最简公分母是(x-1)3,故答案选B.
分式
的最简公分母为(
)
A.(x-1)2
B.
(x-1)3
C.
(x-1)
D.
(x-1)2
(1-x)3
B
知1-讲
总
结
感悟新知
如果各分母都是多项式,确定最简公分母的方法:就要把它们分解因式,然后把每个因式当做一个因数(或一个字母),再按照单项式求最简公分母的方法,从系数、相同因式、不同因式三个方面去求.
知1-练
感悟新知
C
B
知2-导
感悟新知
知识点
通分
2
1.下面再来复习分数的加减运算:
知2-导
感悟新知
2.类比分数的加减运算,下面分式的加减运算如何进行?
知2-导
感悟新知
根据分式的基本性质,把几个异分母的分式化成同分母的分式的过程,叫作分式的通分(reduction
of
fractions
to
a
common
denominator).
知2-讲
感悟新知
分式的通分:化异分母分式为同分母分式的过程叫做分式的通分
知2-讲
感悟新知
要点精析:(1)通分的依据是分式的基本性质.
(2)通分的关键是确定几个分式的最简公分母;
(3)分式→约分;分式→通分.
即:
同乘
同除
约分
通分
知2-讲
感悟新知
例2
通分:
解:(1)最简公分母是12xy2,
知2-讲
感悟新知
(2)最简公分母是a2b2c2,
知2-讲
感悟新知
总
结
确定分母是单项式的分式的最简公分母的方法是:①系数取各分母系数的最小公倍数:②同底数幂取次数最高的作为最简公分母的一个因式;③单独出现的字母连同它的指数作为最简公分母的一个因式.
知2-讲
感悟新知
通分:
例
3
分析:(1)中的分母分别是x,x2-x=x(x-1),因此最简公分母是x(x-1)
(2)中的分母因式分解后,分别是x2-4-(x+2)(x-2),4-2x=-2(x-2),因此最简公分母是2(x+2)(x-2).
知2-讲
感悟新知
解:(1)最简公分母是x(x-1),
(2)最简公分母是2(x+2)(x-2),
知2-讲
感悟新知
总
结
分母是多项式的分式的最简公分母的确定方法:(1)将各个分母因式分解;(2)找出每个出现的因式的最高次幂,它们的积为最简公分母的因式;(3)若有系数,则所有系数的最小公倍数是最简公分母的系数.
课堂小结
分式的通分
(1)分式通分的依据是分式的基本性质.
(2)分式通分的关键是确定几个分式的最简公分母.各分母所有因式的最高次幂的积,叫做最简公分母.最简公分母的组成:凡出现字母(或含字母的式子)为底数的幂的因式,选取指数最大的;当各分母的系数为整数时,取它们系数的最小公倍数做最简公分母的系数;当分母为多项式时,一般应先分解因式.公因式与最简分母的区别:公因式是各项系数的最大公约数与相同因式最低次幂的积,而最简公分母是各分母系数的最小公倍数与所有各个因式最高次幂的积.
课堂小结
(3)
确定最简公分母的一般步骤:①取各分母系数的最小公倍;②凡是在分母中出现的字母为底的幂的因式都要取;③以相同字母为底的幂的因式取指数最大的.当各分母是多项式时,先把各多项式分解因式,再按上面的方法求出各分母的最简公分母.
分式的通分
必做:
请完成教材课后习题
课后作业
作业
同课章节目录
