2021-2022学年人教版九年级数学上册22..1二次函数y=ax2 k的图像与性质课件(共18张)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册22..1二次函数y=ax2 k的图像与性质课件(共18张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-12 13:33:09 | ||
图片预览




文档简介
(共18张PPT)
二次函数y=ax2+k
的图像与性质
学习目标:
掌握二次函数y=ax2
+k的图像与性质,理解二次函数图像的上下平移。
温故知新
y=ax2
(a≠0)
a>0
a<0
图
象
开口方向
顶点坐标
对称轴
增
减
性
极值
x
y
O
y
x
O
向上
向下
(0
,0)
(0
,0)
y轴
y轴
当x<0时,
y随着x的增大而减小。
当x>0时,
y随着x的增大而增大。
当x<0时,
y随着x的增大而增大。
当x>0时,
y随着x的增大而减小。
x=0时,y最小=0
x=0时,y最大=0
抛物线y=ax2
(a≠0)的形状是由|a|来确定的,一般说来,
|a|越大,抛物线的开口就越小.
1.画出y=x2
与
y=x2
+1、
y=x2
-2的图像,并观察彼此的位置关系.
自学检测:
2.画出y=-x2
与
y=-x2
+3、
y=-x2
-2的图像,并观察彼此的位置关系.
x
…..
-2
-1
0
1
2
……
y=x2
……
4
1
0
1
4
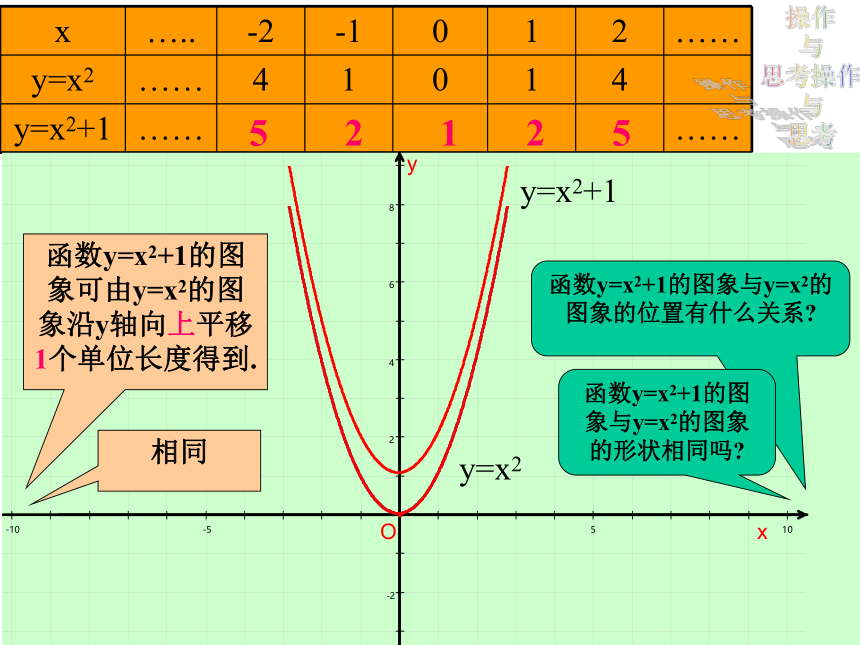
y=x2+1
……
……
y=x2
y=x2+1
5
2
1
2
5
函数y=x2+1的图象与y=x2的图象的位置有什么关系?
函数y=x2+1的图象可由y=x2的图象沿y轴向上平移1个单位长度得到.
操作
与
思考
函数y=x2+1的图象与y=x2的图象的形状相同吗?
相同
x
…..
-2
-1
0
1
2
……
y=x2
……
4
1
0
1
4
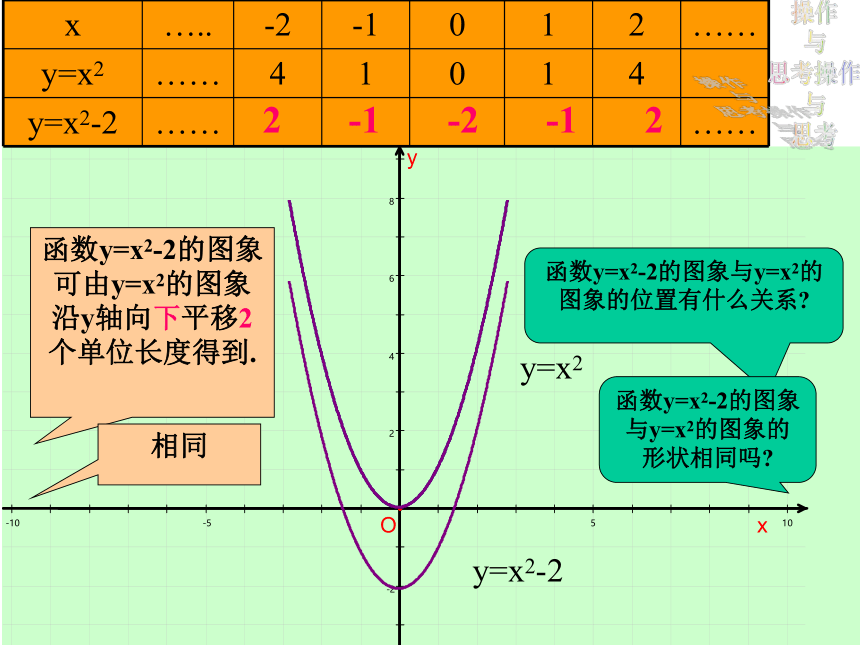
y=x2-2
……
……
y=x2
y=x2-2
2
-1
-2
-1
2
函数y=x2-2的图象可由y=x2的图象沿y轴向下平移2个单位长度得到.
函数y=x2-2的图象与y=x2的图象的位置有什么关系?
操作
与
思考
函数y=x2-2的图象与y=x2的图象的形状相同吗?
相同
函数y=ax2
(a≠0)和函数y=ax2+k
(a≠0)的图象形状
,只是位置不同;当k>0时,函数y=ax2+k的图象可由y=ax2的图象向
平移
个单位得到,当k<0时,函数y=ax2+k的图象可由y=ax2的图象
向
平移
个单位得到。
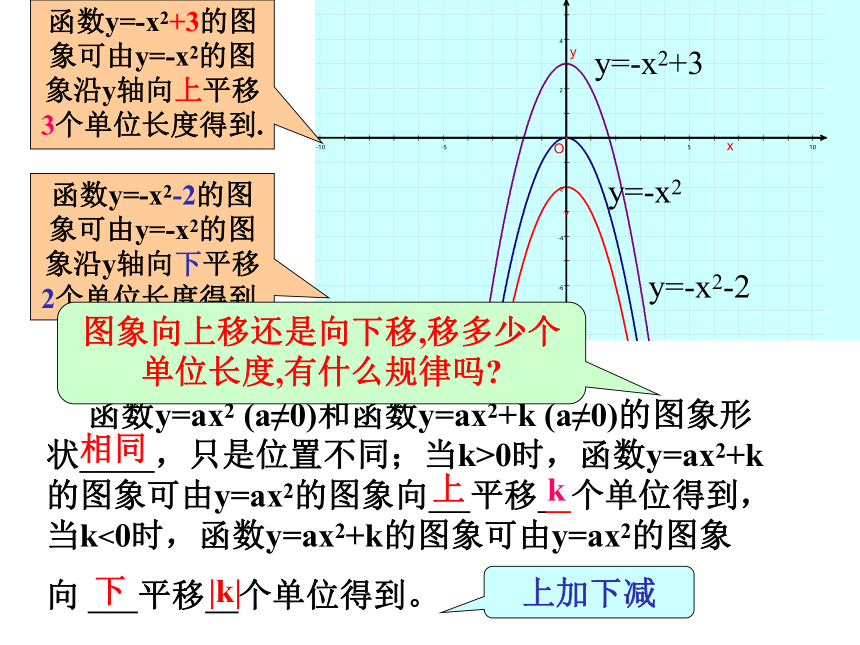
y=-x2-2
y=-x2+3
y=-x2
函数y=-x2-2的图象可由y=-x2的图象沿y轴向下平移2个单位长度得到.
函数y=-x2+3的图象可由y=-x2的图象沿y轴向上平移3个单位长度得到.
图象向上移还是向下移,移多少个单位长度,有什么规律吗?
上加下减
相同
上
k
下
|k|
当a>0时,抛物线y=ax2+k的开口
,对称轴是
,顶点坐标是
,在对称轴的左侧,y随x的增大而
,在对称轴的右侧,y随x的增大而
,
当x=
时,取得最
值,这个值等于
;
当a<0时,抛物线y=ax2+k的开口
,对称轴是
,顶点坐标是
,在对称轴的左侧,y随x的增大而
,在对称轴的右侧,y随x的增大而
,当x=
时,取得最
值,这个值等于
。
y=-x2-2
y=-x2+3
y=-x2
y=x2-2
y=x2+1
y=x2
向上
y轴
(0,k)
减小
增大
0
小
k
向下
y轴
(0,k)
增大
减小
0
大
k
自学检测
y=ax2+k
(a≠0)
a>0
a<0
开口方向
顶点坐标
对称轴
增
减
性
极值
向上
向下
(0
,k)
(0
,k)
y轴
y轴
当x<0时,
y随着x的增大而减小。
当x>0时,
y随着x的增大而增大。
当x<0时,
y随着x的增大而增大。
当x>0时,
y随着x的增大而减小。
x=0时,y最小=k
x=0时,y最大=k
抛物线y=ax2
+c
(a≠0)的图象可由y=ax2的图象通过上下平移得到.
自学检测:
3.
函数y=4x2+5的图象可由y=4x2的图象
向
平移
个单位得到;y=4x2-11的图象
可由
y=4x2的图象向
平移
个单位得到。
5.将抛物线y=4x2向上平移3个单位,所得的
抛物线的函数式是
。
将抛物线y=-5x2+1向下平移5个单位,所得的
抛物线的函数式是
。
4.
将函数y=-3x2+4的图象向
平移
个单位可得
y=-3x2的图象;将y=2x2-7的图象向
平移
个
单位得到可由
y=2x2的图象。将y=x2-7的图象
向
平移
个单位可得到
y=x2+2的图象。
上
5
下
11
下
4
上
7
上
9
y=4x2+3
y=-5x2-4
自学检测:
6.
抛物线y=-3x2+5的开口
,对称轴是
,顶点坐标是
,在对称轴的左侧,y随x的增大而
,在对称轴的右侧,y随x的增大而
,
当x=
时,取得最
值,这个值等于
。
8.二次函数y=ax2+c
(a≠0)的图象经过点A(1,-1),B(2,5),则函数y=ax2+c的表达式为
。若点C(-2,m),D(n
,7)也在函数的图象上,则点C的坐标为
点D的坐标为
.
7.
抛物线y=7x2-3的开口
,对称轴是
,顶点坐标是
,在对称轴的左侧,y随x的增大而
,在对称轴的右侧,y随x的增大而
,
当x=
时,取得最
值,这个值等于
。
下
y轴
(0,5)
减小
增大
0
大
5
上
y轴
(0,-3)
减小
增大
0
小
-3
y=2x2-3
(-2,5)
或
自学检测:
1、抛物线y=-3x2+7的开口____,对称轴是______,顶点坐标是____
4、抛物线y=4x2-1与x轴的交点坐标是____
,与y轴的交点坐标是____.
2、抛物线y=-3x2与抛物线y=ax2-7的形状相同,则a=____.
3、抛物线y=4x2-1向下平移5个单位后,可得抛物线为_____.
基础练习:
下
y轴
(0,7)
-3
y=4x2-6
(±?,0)
(0,-1)
5.已知二次函数y=3x2+4,点A(x1,y1),
B(x2,y2),
C(x3,y3),
D(x4,y4)在其图象上,且x2<
x4<0,
0x1,
|x2|>|x1|,
|x3|>|x4|,
则
(
)
x1
x2
x3
x4
y1
y4
y3
y2
A.y1>y2>y3>y4
B.y2>y1>y3>y4
C.y3>y2>y4>y1
D.y4>y2>y3>y1
B
基础练习:
若二次函数y=(m+1)x2+m2-9有最大值,且图象经过原点,则m=______.
-3
拓展提高
已知点(-3,y1)、(-2,y2)、(-1,y3)都在函数y=2x2-2的图象上,则
y1,y2,y3的大小关系为_____________.
y1>y2>y3
拓展提高
抛物线y=2x2-(m+3)x-m+7的对称轴是y轴,则m=______.
-3
拓展提高
已知一次函数
的图象如右图所示,则二次函数
的图象大致是如下图的(
)
x
y
x
y
o
x
y
o
x
y
o
x
y
o
A
B
C
D
拓展提高
D
本节课学习了什么内容?
二次函数y=ax2+k
的图像与性质
学习目标:
掌握二次函数y=ax2
+k的图像与性质,理解二次函数图像的上下平移。
温故知新
y=ax2
(a≠0)
a>0
a<0
图
象
开口方向
顶点坐标
对称轴
增
减
性
极值
x
y
O
y
x
O
向上
向下
(0
,0)
(0
,0)
y轴
y轴
当x<0时,
y随着x的增大而减小。
当x>0时,
y随着x的增大而增大。
当x<0时,
y随着x的增大而增大。
当x>0时,
y随着x的增大而减小。
x=0时,y最小=0
x=0时,y最大=0
抛物线y=ax2
(a≠0)的形状是由|a|来确定的,一般说来,
|a|越大,抛物线的开口就越小.
1.画出y=x2
与
y=x2
+1、
y=x2
-2的图像,并观察彼此的位置关系.
自学检测:
2.画出y=-x2
与
y=-x2
+3、
y=-x2
-2的图像,并观察彼此的位置关系.
x
…..
-2
-1
0
1
2
……
y=x2
……
4
1
0
1
4
y=x2+1
……
……
y=x2
y=x2+1
5
2
1
2
5
函数y=x2+1的图象与y=x2的图象的位置有什么关系?
函数y=x2+1的图象可由y=x2的图象沿y轴向上平移1个单位长度得到.
操作
与
思考
函数y=x2+1的图象与y=x2的图象的形状相同吗?
相同
x
…..
-2
-1
0
1
2
……
y=x2
……
4
1
0
1
4
y=x2-2
……
……
y=x2
y=x2-2
2
-1
-2
-1
2
函数y=x2-2的图象可由y=x2的图象沿y轴向下平移2个单位长度得到.
函数y=x2-2的图象与y=x2的图象的位置有什么关系?
操作
与
思考
函数y=x2-2的图象与y=x2的图象的形状相同吗?
相同
函数y=ax2
(a≠0)和函数y=ax2+k
(a≠0)的图象形状
,只是位置不同;当k>0时,函数y=ax2+k的图象可由y=ax2的图象向
平移
个单位得到,当k<0时,函数y=ax2+k的图象可由y=ax2的图象
向
平移
个单位得到。
y=-x2-2
y=-x2+3
y=-x2
函数y=-x2-2的图象可由y=-x2的图象沿y轴向下平移2个单位长度得到.
函数y=-x2+3的图象可由y=-x2的图象沿y轴向上平移3个单位长度得到.
图象向上移还是向下移,移多少个单位长度,有什么规律吗?
上加下减
相同
上
k
下
|k|
当a>0时,抛物线y=ax2+k的开口
,对称轴是
,顶点坐标是
,在对称轴的左侧,y随x的增大而
,在对称轴的右侧,y随x的增大而
,
当x=
时,取得最
值,这个值等于
;
当a<0时,抛物线y=ax2+k的开口
,对称轴是
,顶点坐标是
,在对称轴的左侧,y随x的增大而
,在对称轴的右侧,y随x的增大而
,当x=
时,取得最
值,这个值等于
。
y=-x2-2
y=-x2+3
y=-x2
y=x2-2
y=x2+1
y=x2
向上
y轴
(0,k)
减小
增大
0
小
k
向下
y轴
(0,k)
增大
减小
0
大
k
自学检测
y=ax2+k
(a≠0)
a>0
a<0
开口方向
顶点坐标
对称轴
增
减
性
极值
向上
向下
(0
,k)
(0
,k)
y轴
y轴
当x<0时,
y随着x的增大而减小。
当x>0时,
y随着x的增大而增大。
当x<0时,
y随着x的增大而增大。
当x>0时,
y随着x的增大而减小。
x=0时,y最小=k
x=0时,y最大=k
抛物线y=ax2
+c
(a≠0)的图象可由y=ax2的图象通过上下平移得到.
自学检测:
3.
函数y=4x2+5的图象可由y=4x2的图象
向
平移
个单位得到;y=4x2-11的图象
可由
y=4x2的图象向
平移
个单位得到。
5.将抛物线y=4x2向上平移3个单位,所得的
抛物线的函数式是
。
将抛物线y=-5x2+1向下平移5个单位,所得的
抛物线的函数式是
。
4.
将函数y=-3x2+4的图象向
平移
个单位可得
y=-3x2的图象;将y=2x2-7的图象向
平移
个
单位得到可由
y=2x2的图象。将y=x2-7的图象
向
平移
个单位可得到
y=x2+2的图象。
上
5
下
11
下
4
上
7
上
9
y=4x2+3
y=-5x2-4
自学检测:
6.
抛物线y=-3x2+5的开口
,对称轴是
,顶点坐标是
,在对称轴的左侧,y随x的增大而
,在对称轴的右侧,y随x的增大而
,
当x=
时,取得最
值,这个值等于
。
8.二次函数y=ax2+c
(a≠0)的图象经过点A(1,-1),B(2,5),则函数y=ax2+c的表达式为
。若点C(-2,m),D(n
,7)也在函数的图象上,则点C的坐标为
点D的坐标为
.
7.
抛物线y=7x2-3的开口
,对称轴是
,顶点坐标是
,在对称轴的左侧,y随x的增大而
,在对称轴的右侧,y随x的增大而
,
当x=
时,取得最
值,这个值等于
。
下
y轴
(0,5)
减小
增大
0
大
5
上
y轴
(0,-3)
减小
增大
0
小
-3
y=2x2-3
(-2,5)
或
自学检测:
1、抛物线y=-3x2+7的开口____,对称轴是______,顶点坐标是____
4、抛物线y=4x2-1与x轴的交点坐标是____
,与y轴的交点坐标是____.
2、抛物线y=-3x2与抛物线y=ax2-7的形状相同,则a=____.
3、抛物线y=4x2-1向下平移5个单位后,可得抛物线为_____.
基础练习:
下
y轴
(0,7)
-3
y=4x2-6
(±?,0)
(0,-1)
5.已知二次函数y=3x2+4,点A(x1,y1),
B(x2,y2),
C(x3,y3),
D(x4,y4)在其图象上,且x2<
x4<0,
0
|x2|>|x1|,
|x3|>|x4|,
则
(
)
x1
x2
x3
x4
y1
y4
y3
y2
A.y1>y2>y3>y4
B.y2>y1>y3>y4
C.y3>y2>y4>y1
D.y4>y2>y3>y1
B
基础练习:
若二次函数y=(m+1)x2+m2-9有最大值,且图象经过原点,则m=______.
-3
拓展提高
已知点(-3,y1)、(-2,y2)、(-1,y3)都在函数y=2x2-2的图象上,则
y1,y2,y3的大小关系为_____________.
y1>y2>y3
拓展提高
抛物线y=2x2-(m+3)x-m+7的对称轴是y轴,则m=______.
-3
拓展提高
已知一次函数
的图象如右图所示,则二次函数
的图象大致是如下图的(
)
x
y
x
y
o
x
y
o
x
y
o
x
y
o
A
B
C
D
拓展提高
D
本节课学习了什么内容?
同课章节目录
