2021-2022学年苏科版数学九年级上册 -2.8圆锥的侧面积 课件(共15张)
文档属性
| 名称 | 2021-2022学年苏科版数学九年级上册 -2.8圆锥的侧面积 课件(共15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 376.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-12 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
2.8
圆锥的侧面积
九年级(上册)
初中数学
第二章
对称图形—圆
1.弧长公式是什么?
2.扇形的面积公式是什么?
3.大家见过圆锥吗?你们知道圆锥的表面是由哪些面构成的吗?
复习引入
1.圆锥是由一个底面和一个侧面围成的,它的底面是一个圆,侧面是一个曲面.
2.把圆锥底面圆周上的任意一点与圆锥顶点的连线叫做圆锥的母线.
圆锥的再认识
O
S
A
B
r
h
l
A1
A2
问题:圆锥的母线有几条?
请你想一想
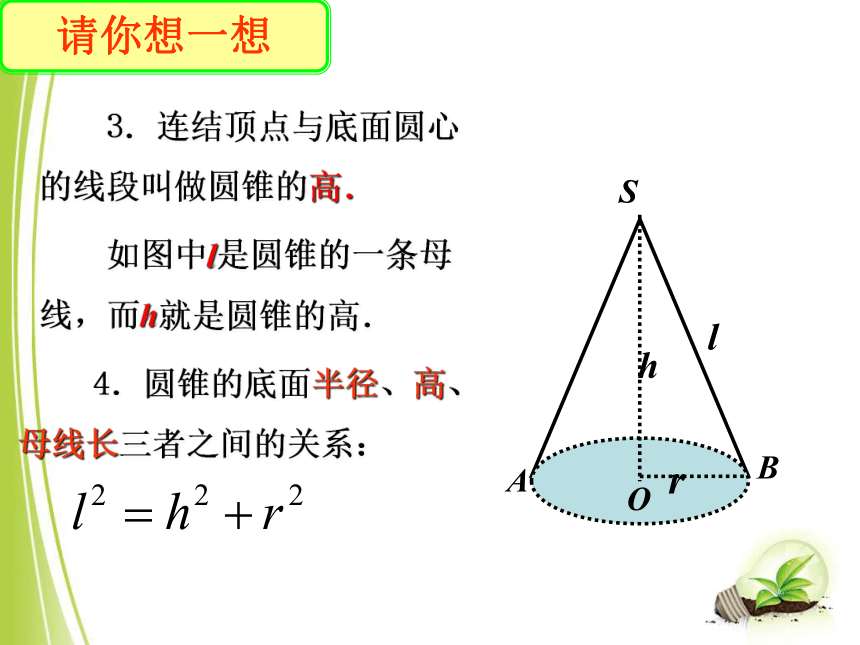
3.连结顶点与底面圆心的线段叫做圆锥的高.
如图中l是圆锥的一条母线,而h就是圆锥的高.
4.圆锥的底面半径、高、母线长三者之间的关系:
O
S
A
B
r
h
l
请你想一想
填空:
根据下列条件求值(其中r、h、
分别是圆锥的底面半径、高线、母线长)
(1)
=
2,r=1
则
h=_______
(2)
=
10,
h
=
8
则r=_______
6
试一试
1.圆锥的侧面展开图是什么形状?
2.圆锥的母线与其侧面展开图扇形的半径有什么关系?
3.圆锥的底面圆周长与侧面展开后扇形的弧长有什么关系?
S
A
O
B
r
扇形
圆锥的母线=扇形的半径
圆锥的底面圆周长=侧面展开后扇形的弧长
实践探索
圆锥的母线长为l,底面的半径为r,求这个圆锥的侧面积.
圆锥的侧面积公式为:
圆锥侧面展开图
实践探索
h
l
r
=
.2πr
.l
=
πr
l
(r是圆锥的底面半径,
l是圆锥的母线长)
例1 用铁皮制作圆锥形容器盖,其尺寸要求如图所示.求所需铁皮的面积S.
典型题例
例2:如图所示的扇形中,半径R=10,圆心角θ=144°用这个扇形围成一个圆锥的侧面.
(1)求这个圆锥的底面半径r;
(2)求这个圆锥的侧面积.
A
C
O
典型题例
B
已知Rt
△ABC中,∠C=90°,AC=4,BC=3,(1)分别以AC,BC所在直线为轴,把三角形ABC旋转一周,求这两个圆锥的侧面积;
(2)以AB所在直线为轴旋转一周,求所得几何体的表面积.
做一做
3
5
A
B
C
4
5
3
4
4
3
5
3
4
O
5
4
2.4
3
1.圆锥的底面半径为3,高为4,则母线长为
,底面的周长为
,侧面展开图的扇形的弧长为
,侧面积为
.
练一练
2.一个扇形,半径为30cm,圆心角为120°,用它做成一个圆锥的侧面,那么这个圆锥的底面半径为
.
5
6π
6π
15π
10cm
3.一个圆锥形零件的高30cm,底面半径40cm,求这个圆锥形零件的侧面积.
练一练
4.如图,在四边形ABCD中,AD∥BC,AD=2,AB=2
,以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F.用扇形AFD围成一个圆锥的侧面,求这个圆锥底面圆的半径。
在半径为 的圆形纸片中,剪一个圆心角为90°的扇形(如图中的阴影部分).
(1)求这个扇形的面积(结果保留π);
拓展提升
(2)用所剪的扇形纸片围成一个圆锥
的侧面,求这个圆锥的底面圆半径.
A
C
O
B
A
A
A
A
A
A
本节课我们有什么收获?
1、认识了圆锥的侧面展开图,学会计算圆锥的侧面积。
2、在认识圆锥的侧面展开图时,知道圆锥的底面周长就是其侧面展开图扇形的弧长,圆锥的母线就是其侧面展开图扇形的半径。
课堂总结
2.8
圆锥的侧面积
九年级(上册)
初中数学
第二章
对称图形—圆
1.弧长公式是什么?
2.扇形的面积公式是什么?
3.大家见过圆锥吗?你们知道圆锥的表面是由哪些面构成的吗?
复习引入
1.圆锥是由一个底面和一个侧面围成的,它的底面是一个圆,侧面是一个曲面.
2.把圆锥底面圆周上的任意一点与圆锥顶点的连线叫做圆锥的母线.
圆锥的再认识
O
S
A
B
r
h
l
A1
A2
问题:圆锥的母线有几条?
请你想一想
3.连结顶点与底面圆心的线段叫做圆锥的高.
如图中l是圆锥的一条母线,而h就是圆锥的高.
4.圆锥的底面半径、高、母线长三者之间的关系:
O
S
A
B
r
h
l
请你想一想
填空:
根据下列条件求值(其中r、h、
分别是圆锥的底面半径、高线、母线长)
(1)
=
2,r=1
则
h=_______
(2)
=
10,
h
=
8
则r=_______
6
试一试
1.圆锥的侧面展开图是什么形状?
2.圆锥的母线与其侧面展开图扇形的半径有什么关系?
3.圆锥的底面圆周长与侧面展开后扇形的弧长有什么关系?
S
A
O
B
r
扇形
圆锥的母线=扇形的半径
圆锥的底面圆周长=侧面展开后扇形的弧长
实践探索
圆锥的母线长为l,底面的半径为r,求这个圆锥的侧面积.
圆锥的侧面积公式为:
圆锥侧面展开图
实践探索
h
l
r
=
.2πr
.l
=
πr
l
(r是圆锥的底面半径,
l是圆锥的母线长)
例1 用铁皮制作圆锥形容器盖,其尺寸要求如图所示.求所需铁皮的面积S.
典型题例
例2:如图所示的扇形中,半径R=10,圆心角θ=144°用这个扇形围成一个圆锥的侧面.
(1)求这个圆锥的底面半径r;
(2)求这个圆锥的侧面积.
A
C
O
典型题例
B
已知Rt
△ABC中,∠C=90°,AC=4,BC=3,(1)分别以AC,BC所在直线为轴,把三角形ABC旋转一周,求这两个圆锥的侧面积;
(2)以AB所在直线为轴旋转一周,求所得几何体的表面积.
做一做
3
5
A
B
C
4
5
3
4
4
3
5
3
4
O
5
4
2.4
3
1.圆锥的底面半径为3,高为4,则母线长为
,底面的周长为
,侧面展开图的扇形的弧长为
,侧面积为
.
练一练
2.一个扇形,半径为30cm,圆心角为120°,用它做成一个圆锥的侧面,那么这个圆锥的底面半径为
.
5
6π
6π
15π
10cm
3.一个圆锥形零件的高30cm,底面半径40cm,求这个圆锥形零件的侧面积.
练一练
4.如图,在四边形ABCD中,AD∥BC,AD=2,AB=2
,以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F.用扇形AFD围成一个圆锥的侧面,求这个圆锥底面圆的半径。
在半径为 的圆形纸片中,剪一个圆心角为90°的扇形(如图中的阴影部分).
(1)求这个扇形的面积(结果保留π);
拓展提升
(2)用所剪的扇形纸片围成一个圆锥
的侧面,求这个圆锥的底面圆半径.
A
C
O
B
A
A
A
A
A
A
本节课我们有什么收获?
1、认识了圆锥的侧面展开图,学会计算圆锥的侧面积。
2、在认识圆锥的侧面展开图时,知道圆锥的底面周长就是其侧面展开图扇形的弧长,圆锥的母线就是其侧面展开图扇形的半径。
课堂总结
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
