3.3 整式课件(共28张PPT)
图片预览








文档简介
第三章 整式及其加减
3 整式
知识点一 单项式及其有关概念
?
定义
示例
单项式
由数与字母的乘积组成的式子叫做单项式.单独的一个数或一个字母也是单项式
100t, mn, -a2h都是单项式,其中100t的系数是100,次数是1;mn的系数是1,次数是2;-a2h的系数是-1,次数是3
系数
单项式中的数字因数叫做这个单项式的系数
次数
一个单项式中,所有字母的指数的和叫做这个单项式的次数
知识点一 单项式及其有关概念
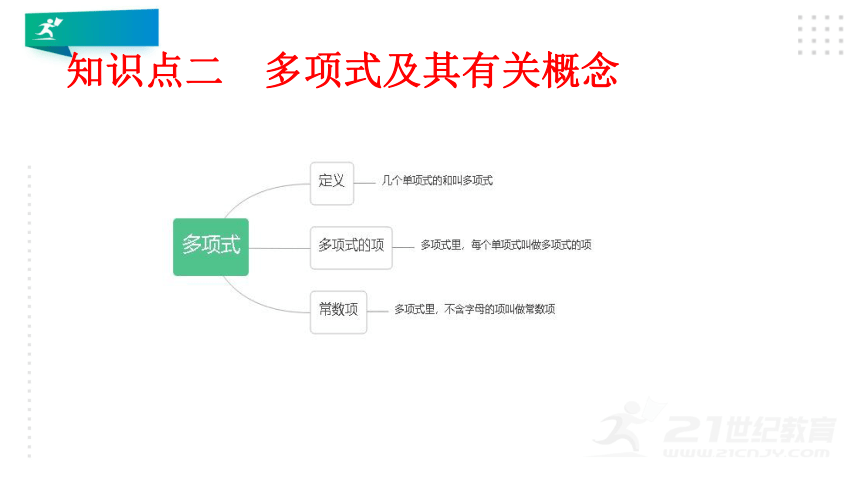
知识点二 多项式及其有关概念
例2 指出下列各多项式的项.
(1)a3-a2b+ab2-b3; (2)3n4-2n2+1.
例2 指出下列各多项式的项.
(1)a3-a2b+ab2-b3; (2)3n4-2n2+1.
解析 (1)多项式a3-a2b+ab2-b3的项是a3,-a2b,ab2,-b3.
(2)多项式3n4-2n2+1的项是3n4,-2n2,1.
例2 指出下列各多项式的项.
(1)a3-a2b+ab2-b3; (2)3n4-2n2+1.
解析 (1)多项式a3-a2b+ab2-b3的项是a3,-a2b,ab2,-b3.
(2)多项式3n4-2n2+1的项是3n4,-2n2,1.
特别提示
多项式的项包括它前面的符号.
知识点三 整式
?
定义
示例
整式
单项式与多项式统称整式
单项式3a,0.8,2st,b2c,-3d,以及多项式2v+1,5x+3y+4z,3ac+2π,都是整式
温馨提示
(1)任意一个整式或者是单项式,或者是多项式,二者必居其一.
(2)一个式子如果不是整式,那么这个式子一定不是单项式或多项式
经典例题
题型一 根据单项式、多项式的相关概念
例1 已知x2y|a|+(b+2)是关于x、y的五次单项式,求a2-3ab的值.
题型一 根据单项式、多项式的相关概念
例1 已知x2y|a|+(b+2)是关于x、y的五次单项式,求a2-3ab的值.
解析 ∵x2y|a|+(b+2)是关于x、y的五次单项式,
∴2+|a|=5,b+2=0,解得a=±3,b=-2,
当a=-3,b=-2时,a2-3ab=9-18=-9;
当a=3,b=-2时,a2-3ab=9+18=27.
题型一 根据单项式、多项式的相关概念
例1 已知x2y|a|+(b+2)是关于x、y的五次单项式,求a2-3ab的值.
解析 ∵x2y|a|+(b+2)是关于x、y的五次单项式,
∴2+|a|=5,b+2=0,解得a=±3,b=-2,
当a=-3,b=-2时,a2-3ab=9-18=-9;
当a=3,b=-2时,a2-3ab=9+18=27.
特别提示
2+|a|=5的解有两种情况,解题时注意不要漏解.
题型二 关于单项式的规律探究问题
例2 有一列单项式-x,2x2,-3x3,…,-19x19,20x20,….
(1)根据你发现的规律,写出该列单项式中第100个,第101个,第102个单项式;
(2)你能进一步写出第n个单项式吗?
题型二 关于单项式的规律探究问题
例2 有一列单项式-x,2x2,-3x3,…,-19x19,20x20,….
(1)根据你发现的规律,写出该列单项式中第100个,第101个,第102个单项式;
(2)你能进一步写出第n个单项式吗?
解析(1)第100个,第101个,第102个单项式分别是100x100,-101x101,102x102.
(2)第n个单项式是(-1)n·nxn.
题型二 关于单项式的规律探究问题
例2 有一列单项式-x,2x2,-3x3,…,-19x19,20x20,….
(1)根据你发现的规律,写出该列单项式中第100个,第101个,第102个单项式;
(2)你能进一步写出第n个单项式吗?
解析(1)第100个,第101个,第102个单项式分别是100x100,-101x101,102x102.
(2)第n个单项式是(-1)n·nxn.
点拨 对于整式排列的规律探究题,主要是探究指数和系数的规律,注意系数符号的规律.
易错易混
易错点 对单项式系数和次数的概念理解不透彻,导致错误
没有从本质上理解单项式系数和次数的概念易导致出错,应当把单项式分为数字因数和字母因数两部分,数字因数就是系数,而所有字母的指数之和就是次数,丢失任何一个数字因数或某个字母的指数都是错误的.
3 整式
知识点一 单项式及其有关概念
?
定义
示例
单项式
由数与字母的乘积组成的式子叫做单项式.单独的一个数或一个字母也是单项式
100t, mn, -a2h都是单项式,其中100t的系数是100,次数是1;mn的系数是1,次数是2;-a2h的系数是-1,次数是3
系数
单项式中的数字因数叫做这个单项式的系数
次数
一个单项式中,所有字母的指数的和叫做这个单项式的次数
知识点一 单项式及其有关概念
知识点二 多项式及其有关概念
例2 指出下列各多项式的项.
(1)a3-a2b+ab2-b3; (2)3n4-2n2+1.
例2 指出下列各多项式的项.
(1)a3-a2b+ab2-b3; (2)3n4-2n2+1.
解析 (1)多项式a3-a2b+ab2-b3的项是a3,-a2b,ab2,-b3.
(2)多项式3n4-2n2+1的项是3n4,-2n2,1.
例2 指出下列各多项式的项.
(1)a3-a2b+ab2-b3; (2)3n4-2n2+1.
解析 (1)多项式a3-a2b+ab2-b3的项是a3,-a2b,ab2,-b3.
(2)多项式3n4-2n2+1的项是3n4,-2n2,1.
特别提示
多项式的项包括它前面的符号.
知识点三 整式
?
定义
示例
整式
单项式与多项式统称整式
单项式3a,0.8,2st,b2c,-3d,以及多项式2v+1,5x+3y+4z,3ac+2π,都是整式
温馨提示
(1)任意一个整式或者是单项式,或者是多项式,二者必居其一.
(2)一个式子如果不是整式,那么这个式子一定不是单项式或多项式
经典例题
题型一 根据单项式、多项式的相关概念
例1 已知x2y|a|+(b+2)是关于x、y的五次单项式,求a2-3ab的值.
题型一 根据单项式、多项式的相关概念
例1 已知x2y|a|+(b+2)是关于x、y的五次单项式,求a2-3ab的值.
解析 ∵x2y|a|+(b+2)是关于x、y的五次单项式,
∴2+|a|=5,b+2=0,解得a=±3,b=-2,
当a=-3,b=-2时,a2-3ab=9-18=-9;
当a=3,b=-2时,a2-3ab=9+18=27.
题型一 根据单项式、多项式的相关概念
例1 已知x2y|a|+(b+2)是关于x、y的五次单项式,求a2-3ab的值.
解析 ∵x2y|a|+(b+2)是关于x、y的五次单项式,
∴2+|a|=5,b+2=0,解得a=±3,b=-2,
当a=-3,b=-2时,a2-3ab=9-18=-9;
当a=3,b=-2时,a2-3ab=9+18=27.
特别提示
2+|a|=5的解有两种情况,解题时注意不要漏解.
题型二 关于单项式的规律探究问题
例2 有一列单项式-x,2x2,-3x3,…,-19x19,20x20,….
(1)根据你发现的规律,写出该列单项式中第100个,第101个,第102个单项式;
(2)你能进一步写出第n个单项式吗?
题型二 关于单项式的规律探究问题
例2 有一列单项式-x,2x2,-3x3,…,-19x19,20x20,….
(1)根据你发现的规律,写出该列单项式中第100个,第101个,第102个单项式;
(2)你能进一步写出第n个单项式吗?
解析(1)第100个,第101个,第102个单项式分别是100x100,-101x101,102x102.
(2)第n个单项式是(-1)n·nxn.
题型二 关于单项式的规律探究问题
例2 有一列单项式-x,2x2,-3x3,…,-19x19,20x20,….
(1)根据你发现的规律,写出该列单项式中第100个,第101个,第102个单项式;
(2)你能进一步写出第n个单项式吗?
解析(1)第100个,第101个,第102个单项式分别是100x100,-101x101,102x102.
(2)第n个单项式是(-1)n·nxn.
点拨 对于整式排列的规律探究题,主要是探究指数和系数的规律,注意系数符号的规律.
易错易混
易错点 对单项式系数和次数的概念理解不透彻,导致错误
没有从本质上理解单项式系数和次数的概念易导致出错,应当把单项式分为数字因数和字母因数两部分,数字因数就是系数,而所有字母的指数之和就是次数,丢失任何一个数字因数或某个字母的指数都是错误的.
