【备战2012】高考数学(理) 最新专题冲刺之函数
文档属性
| 名称 | 【备战2012】高考数学(理) 最新专题冲刺之函数 |
|
|
| 格式 | zip | ||
| 文件大小 | 996.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-31 00:00:00 | ||
图片预览



文档简介
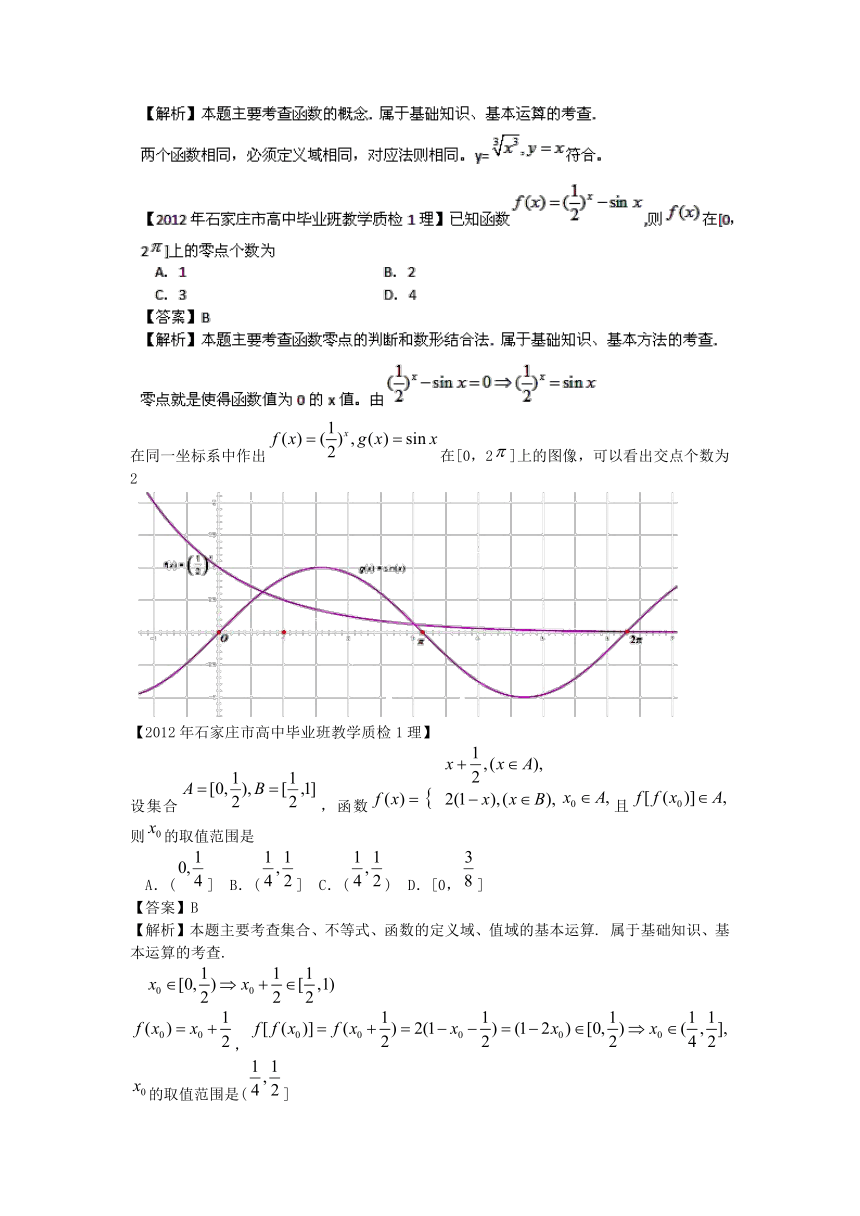
【江西省新钢中学2012届高三模拟考试】9.函数的值域为
A. B. C. D.
【解】:的定义域为则,令,则
因,则 .
【解析】本题主要考查分段函数、指数的运算. 属于基础知识、基本运算的考查.
∵ ∴
【2012唐山市高三模拟统一考试理】函数的定义域为 ( )
A. B. C. D.
【答案】 B
【解析】本题主要考查函数的定义域、对数不等式的解法. 属于基础知识、基本运算的考查.
由
【2012唐山市高三模拟统一考试】设,则函数的零点位于区间( )
A.(-1,0) B.(0,1) C.(1,2) D.(2,3)
【答案】 C
【2012唐山市高三上学期模拟统一考试理】已知,则= ( )
A. B.1 C. D.2
【答案】 D
【解析】本题主要考查指数和对数的互化以及对数的运算公式. 属于基础知识、基本运算
的考查.
∵ ∴
;
【2012年石家庄市高中毕业班教学质检1理】下列函数中与函数y=x相等的是
A.y=|x| B.y= C.y= D.y=
【答案】D
在同一坐标系中作出在[0,2]上的图像,可以看出交点个数为2
【2012年石家庄市高中毕业班教学质检1理】
设集合,函数且 则的取值范围是
A.(] B.(] C.() D.[0,]
【答案】B
【解析】本题主要考查集合、不等式、函数的定义域、值域的基本运算. 属于基础知识、基本运算的考查.
,
的取值范围是(]
【2012三明市普通高中高三联考理】函数的零点所在区间是
A. B.
C.(1,2) D.
【答案】B
【解析】本题主要考查函数点的概念、数形结合的解题方法. 属于基础知识、基本方法的考查.
由=0得,零点个数即是和的图像交点的个数,在同一坐标系中分别作出和的图像,易知零点个数为1
【2012三明市普通高中高三联考理】已知函数是奇函数,当时,=,则的值等于
A. B. C. D.
【答案】D
【解析】本题主要考查函数的奇偶性、分段函数以及分段函数值的求法计算,属于基础知识、基本计算的考查.
当时,=,∴,
是奇函数,∴
【2012黄冈市高三模拟考试理】设,则使得为奇函数,且在上单调递减的n的个数为( )
A.1 B.2 C.3 D.4
【答案】 A
【解析】本题主要考查幂函数及其单调性判断. 属于基础知识、基本运算的考查.
设,则使得为奇函数,且在上单调递减的函数是一个.
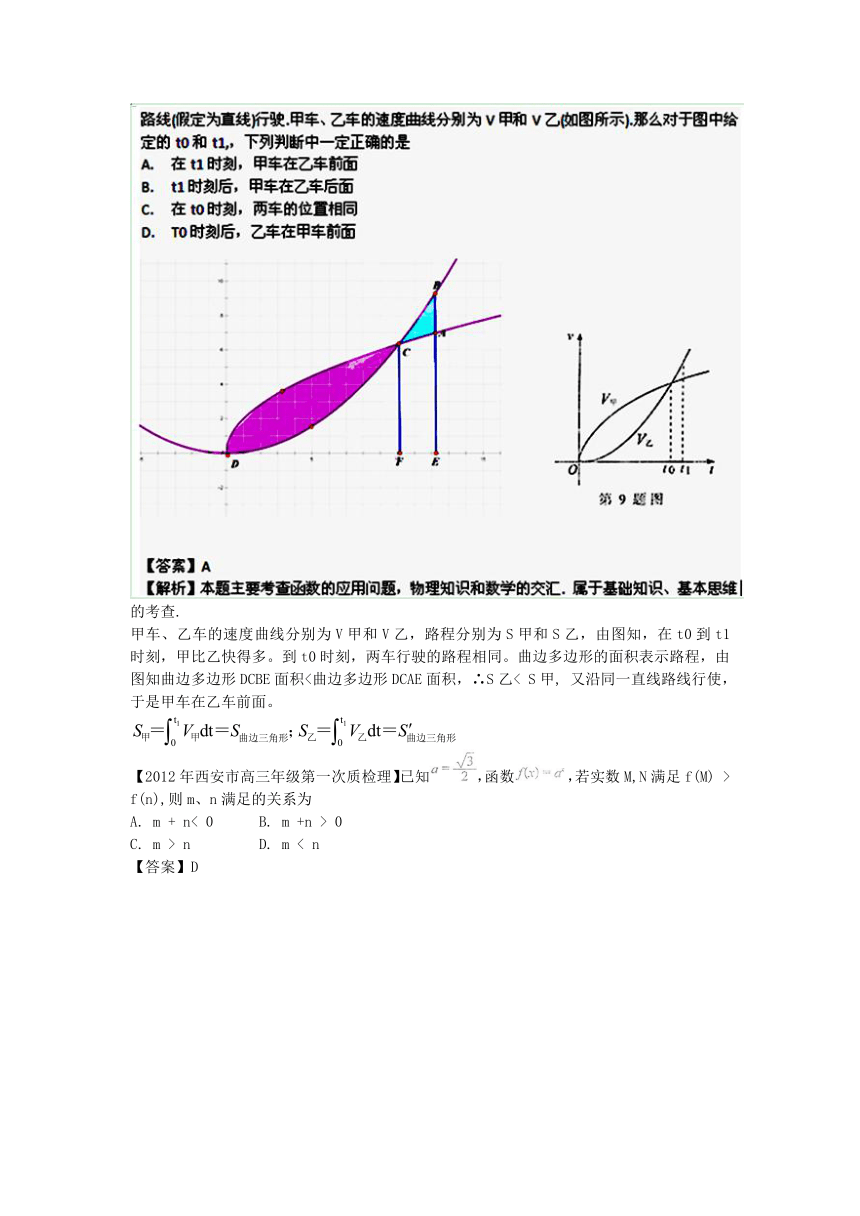
【2012年西安市高三年级第一次质检理】已知甲、乙两车由同一起点同时出发,并沿同一的考查.
甲车、乙车的速度曲线分别为V甲和V乙,路程分别为S甲和S乙,由图知,在t0到t1时刻,甲比乙快得多。到t0时刻,两车行驶的路程相同。曲边多边形的面积表示路程,由图知曲边多边形DCBE面积<曲边多边形DCAE面积,∴S乙< S甲, 又沿同一直线路线行使,于是甲车在乙车前面。
【2012年西安市高三年级第一次质检理】已知,函数,若实数M,N满足f(M) > f(n),则m、n满足的关系为
A. m + n< 0 B. m +n > 0
C. m > n D. m < n
【答案】D
在区间上的值域为,则函数在上的值域为( )
(A) (B) (C) (D)
【答案】B
【解析】由题可设,,由周期性可知,,,,同理,,,……,,,故函数在上的值域为。
【2012浙江宁波市模拟理】函数的定义域为 .
【答案】
【解析】由题可得,解得。
【答案】A
【解析】由题可知函数的周期为4,故。
【2012江西南昌市调研理】函数的值域为 ( )
A.[1,+∞) B.(0,1] C.(-∞,1] D.(-∞,1)
【答案】C
【解析】因,所以,即,选C。
【2012广东佛山市质检理】下列函数中既是奇函数,又在区间上是增函数的为( )
A. B. C. D.
【答案】B
【解析】由题中选项可知,,为偶函数,排除A、C;而在R上递减,故选B。
【2012广东佛山市质检理】对任意实数,函数,如果函数,那么函数的最大值等于 .
【答案】
【解析】令,则可得,令,则,即为奇函数,令,则,所以,即递减,
又,因,所以,即,故选B。
【2012北京海淀区模拟理】已知函数,则下列结论正确的是( )
(A)是偶函数,递增区间是 (B)是偶函数,递减区间是
(C)是奇函数,递减区间是 (D)是奇函数,递增区间是
【答案】C
【2012黄冈市高三上学期模拟考试理】函数,则函数的零点个数有 个。
【答案】 2
【解析】本题主要考查. 属于基础知识、基本运算的考查.
∵分别作出、的图像,知交点数即零点数为2
【2012武昌区高三年级调研理】函数的图象如图所示,给出以下说法:
①函数的定义域是[一l,5];
②函数的值域是(一∞,0]∪[2,4];
③函数在定义域内是增函数;
④函数在定义域内的导数
其中正确的是 ( )
A.①② B.①③ C.②③ D.②④
【答案】A
【解析】本题主要考查函数的图像与性质. 属于基础知识的考查.
的定义域中含有,①②正确;函数在定义域内不是增函数,因而③④错误。
【2012武昌区高三年级元月调研理】若 ( )
A. B. C. D.
【答案】D
【解析】本题主要考查对数的基本运算以及指数的运算. 属于基础知识、基本运算的考查.
由,,所以
【2012厦门模拟质检理10】已知函数f(x)=则下列结论正确的是
A.f(x)在(-1,0)上恰有一个零点 B. f(x)在(0,1)上恰有一个零点
C.f(x)在(-1,0)上恰有两个零点 D. f(x)在(0,1)上恰有两个零点
【答案】A
【解析】因为函数f(x)=在单调增,,选A;
【2012厦门模拟质检理13】定义区间[x1,x2]( x1的定义域为[a,b],值域为[0,8],则区间[a,b]长度的最大值等于 。
【答案】
【答案】B
【解析】因为奇函数在上的解析式是,取
【2012宁德质检理10】若函数在给定区间M上,存在正数t,使得对于任意,有,且,则称为M上的t级类增函数,则以下命题正确的是 ( )
A.函数上的1级类增函数
B.函数上的1级类增函数
C.若函数上的级类增函数,则实数a的最小值为2
D.若函数上的t级类增函数,则实数t的取值范围为
【答案】D
【2012深圳中学模拟理5】值域为{2,5,10},其对应关系为的函数的个数 ( )
A . 1 B. 27
C. 39 D. 8
【答案】B
【解析】解:分别由解得由函数的定义,定义域中元素的选取分四种情况:
1取三个元素:有C21种
2取四个元素:先从三组中选取一组再从剩下的两组中选两个元素,故共有种;
3取五个元素:=6种;
4取六个元素:1种。
由分类计数原理,共有8+12+6+1=27种。
【2012深圳中学模拟理6】设函数,则满足方程根的个数是( )
A.1 个 B.2 个 C.3 个 D.无数个
【答案】C
【解析】方法一:详细画出f(x)和g(x)在同一坐标系中函数图象,由图5中不难看出有三个交点,故选C
方法二:①当时,,则
②当时,,则
③当时,,则
④当时,,则
⑤当时,,则
由此下区x的解成指数增长,而区间成正比增长,故以后没有根了!所以应选C。
【2012海南嘉积中学模拟理12】规定表示两个数中的最小的数,,若函数的图像关于直线对称,则的值是( )
A、-1 B、1 C、-2 D、2
【答案】B
【解析】的图像关于直线对称,,
【2012海南嘉积中学模拟理15】若函数,若,则实数的取值范围是 .
数,当时,设函数的值域为集合,记中的元素个数为,则使为最小时的是( )
A.7 B.9 C.10 D.13
【答案】C
【解析】时,时,,;,取得最小值。
【2012浙江瑞安模拟质检理17】对于函数,若存在区间,当时的值域为,则称为倍值函数.若是倍值函数,则实数的取值范围是 .
【2012武昌区高三年级调研理】某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为,其中为销售量(单位:辆).若该公司在这两地共销售15辆车,则能获得的最大利润为 万元.
【答案】 45.6
【解析】本题主要考查函数的应用问题及二次函数的最值. 属于基础知识、基本运算的考查.
设甲地销量为辆,则乙地销量为15-辆,总利润为y(单位:万元),则
,
即 二次函数对称轴为
∵,故辆时y最大,最大值为45.6万元。
【2012黄冈市高三模拟考试理】某工厂生产一种产品的原材料费为每件40元,若用x表示该厂生产这种产品的总件数,则电力与机器保养等费用为每件0.05x元,又该厂职工工资固定支出12500元。
(1)把每件产品的成本费P(x)(元)表示成产品件数x的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量x不超过3000件,且产品能全部销售,根据市场调查:每件产品的销售价Q(x)与产品件数x有如下关系:,试问生产多少件产品,总利润最高?(总利润=总销售额-总的成本)
【解析】本题主要考查函数的应用问题、逻辑思维能力、推理论证能力.
【2012宁德质检理】(本小题满分13分)
已知函数
(1)若函数为奇函数,求实数k的值;
(2)若对任意的都有成立,求实数k的取值范围。
【2012深圳中学模拟理】(本小题满分14分)
已知集合.其中 为正常数.
(I)设,求的取值范围.
(II)求证:当时不等式对任意恒成立;
(III)求使不等式对任意恒成立的的范围.
【答案】(I),当且仅当时等号成立,
故的取值范围为.(3分)
(II) 变形,得
. (5分)
由,又,,∴在上是增函数,
所以.
即当时不等式成立. (9分)
【2012·泉州四校二次联考理】(本小题满分13分)
省环保研究所对市中心每天环境放射性污染情况进行调查研究后,发现一天中环境综合放射性污染指数与时刻(时)的关系为,
其中是与气象有关的参数,且,若用每天的最大值为当天的综合放射性污染指数,并记作.
(1)令,,求t的取值范围;
(2)省政府规定,每天的综合放射性污染指数不得超过2,试问目前市中心的综合放射性污染指数是否超标?
(本小题满分13分)
【解】(1)当时,t=0; ……………………1分
当时,(当时取等号),
∴,
【2012厦门市高三模拟理】设函数f(x)=-x3+mx2+x,g(x)=mx2-x+c,F(x)=x f(x)。
(Ⅰ) 若函数y= f(x)在x=2处有极值,求实数m的值;
(Ⅱ) 试讨论方程y=F'(x)=g(x)的实数解的个数;
(Ⅲ)记函数y= G(x)的导称函数G'( x)在区间(a,b)上的导函数为G''( x),若在(a,b)上G''( x)>0恒成立,则称函数G(x) (a,b)上为“凹函数”。若存在实数m∈[-2,2],使得函数F(x)在(a,b)上为“凹函数”,求b-a最大值。
【解析】本题主要考查函数、导数知识及其应用,考查运算求解能力及抽象概括能力,考查函数与方程、分类与整合、数形结合、化归与转化等思想方法.
(II)F'(x)=
F'(x)=g(x), 即,即
令,则
∵
∴
由图知,
当时,F'(x)=g(x)的实数解的个数为1
当时,F'(x)=g(x)的实数解的个数为2
当时,F'(x)=g(x)的实数解的个数为3
当时,F'(x)=g(x)的实数解的个数为2
的两根为,则
,m∈[-2,2]
的最大值为,故,从而b-a最大值为
(Ⅱ), , ………………8分
,
……………………10分
即: .
的取值范围………………12分
【2012武昌区高三年级调研理】已知函数为R上的奇函数,的导数为,且当时,不等式成立,若对一切恒成立,则实数的取值范围是 。
【答案】
(1)求函数的极大值点;
(2)当时,若在上至少存在一点,使成立,求的取值范围.
【解析】本题主要考查了导数的计算、导数与单调性的关系、极值问题以及恒成立问题。属于难题。考查了基础知识、基本运算、基本变换能力和转换的思想、分类讨论的思想.
由(1)知,①当,即时,
综上所述,当时,在上至少存在一点,使成立。
【2012三明市普通高中高三联考理】已知函数图象上点处的 令得 ,则此方程在上恰有两解。 ………8分
记
得 ………10分
v
的图像如图所示(或 ) ………………………13分
. ………………………14分
【2012黄冈市高三模拟考试理】已知函数
(1)曲线经过点P(1,2),且曲线C在点P处的切线平行于直线,求a,b的值;
(2)在(1)的条件下试求函数的极小值;
(3)若在区间(1,2)内存在两个极值点,求证:
【解析】本题主要考查函数、导数知识及其应用,考查运算求解能力及抽象概括能力,考查函数与方程、分类与整合、数形结合、化归与转化等思想方法.
【解】(1)=,
由题设知: 解得………………………4分
(Ⅱ)由(1)知
=mx(x-),当m>0时,g(x)在(-,0),(,+)上递增,在(0,)上递减,所以g(x)的极小值为g()=-m;当m<0时,g(x)在(-,0),(,+)上递减,在(0,)上递增,所以g(x)的极小值为g(0)=0;……8分
(Ⅲ)因为在区间内存在两个极值点,所以,
即在内有两个不等的实根.
∴ ……………………………11分
由 (1)+(3)得,由(4)得,
∴,又,∴.
故a+b的取值范围是(0,2)……………………………14分
【2012武昌区高三年级模拟理】已知函数
(Ⅰ)求函数的单调区间;
(Ⅱ)若恒成立,试确定实数k的取值范围;
(Ⅲ)证明:
而不成立,故.
当时,由(Ⅰ)知.
要使恒成立,则即可.
故,解得.
(Ⅲ)由(Ⅱ)知,当时有在恒成立,且在上是减函数,,
所以且, …………4分
(I)因为为的极大值点,所以
当时,;当时,;当时,
所以的递增区间为,;递减区间为.…………7分
(II)①若,则在上递减,在上递增
恰有两解,则,即,所以;
②若,则,
A. B. C. D.
【解】:的定义域为则,令,则
因,则 .
【解析】本题主要考查分段函数、指数的运算. 属于基础知识、基本运算的考查.
∵ ∴
【2012唐山市高三模拟统一考试理】函数的定义域为 ( )
A. B. C. D.
【答案】 B
【解析】本题主要考查函数的定义域、对数不等式的解法. 属于基础知识、基本运算的考查.
由
【2012唐山市高三模拟统一考试】设,则函数的零点位于区间( )
A.(-1,0) B.(0,1) C.(1,2) D.(2,3)
【答案】 C
【2012唐山市高三上学期模拟统一考试理】已知,则= ( )
A. B.1 C. D.2
【答案】 D
【解析】本题主要考查指数和对数的互化以及对数的运算公式. 属于基础知识、基本运算
的考查.
∵ ∴
;
【2012年石家庄市高中毕业班教学质检1理】下列函数中与函数y=x相等的是
A.y=|x| B.y= C.y= D.y=
【答案】D
在同一坐标系中作出在[0,2]上的图像,可以看出交点个数为2
【2012年石家庄市高中毕业班教学质检1理】
设集合,函数且 则的取值范围是
A.(] B.(] C.() D.[0,]
【答案】B
【解析】本题主要考查集合、不等式、函数的定义域、值域的基本运算. 属于基础知识、基本运算的考查.
,
的取值范围是(]
【2012三明市普通高中高三联考理】函数的零点所在区间是
A. B.
C.(1,2) D.
【答案】B
【解析】本题主要考查函数点的概念、数形结合的解题方法. 属于基础知识、基本方法的考查.
由=0得,零点个数即是和的图像交点的个数,在同一坐标系中分别作出和的图像,易知零点个数为1
【2012三明市普通高中高三联考理】已知函数是奇函数,当时,=,则的值等于
A. B. C. D.
【答案】D
【解析】本题主要考查函数的奇偶性、分段函数以及分段函数值的求法计算,属于基础知识、基本计算的考查.
当时,=,∴,
是奇函数,∴
【2012黄冈市高三模拟考试理】设,则使得为奇函数,且在上单调递减的n的个数为( )
A.1 B.2 C.3 D.4
【答案】 A
【解析】本题主要考查幂函数及其单调性判断. 属于基础知识、基本运算的考查.
设,则使得为奇函数,且在上单调递减的函数是一个.
【2012年西安市高三年级第一次质检理】已知甲、乙两车由同一起点同时出发,并沿同一的考查.
甲车、乙车的速度曲线分别为V甲和V乙,路程分别为S甲和S乙,由图知,在t0到t1时刻,甲比乙快得多。到t0时刻,两车行驶的路程相同。曲边多边形的面积表示路程,由图知曲边多边形DCBE面积<曲边多边形DCAE面积,∴S乙< S甲, 又沿同一直线路线行使,于是甲车在乙车前面。
【2012年西安市高三年级第一次质检理】已知,函数,若实数M,N满足f(M) > f(n),则m、n满足的关系为
A. m + n< 0 B. m +n > 0
C. m > n D. m < n
【答案】D
在区间上的值域为,则函数在上的值域为( )
(A) (B) (C) (D)
【答案】B
【解析】由题可设,,由周期性可知,,,,同理,,,……,,,故函数在上的值域为。
【2012浙江宁波市模拟理】函数的定义域为 .
【答案】
【解析】由题可得,解得。
【答案】A
【解析】由题可知函数的周期为4,故。
【2012江西南昌市调研理】函数的值域为 ( )
A.[1,+∞) B.(0,1] C.(-∞,1] D.(-∞,1)
【答案】C
【解析】因,所以,即,选C。
【2012广东佛山市质检理】下列函数中既是奇函数,又在区间上是增函数的为( )
A. B. C. D.
【答案】B
【解析】由题中选项可知,,为偶函数,排除A、C;而在R上递减,故选B。
【2012广东佛山市质检理】对任意实数,函数,如果函数,那么函数的最大值等于 .
【答案】
【解析】令,则可得,令,则,即为奇函数,令,则,所以,即递减,
又,因,所以,即,故选B。
【2012北京海淀区模拟理】已知函数,则下列结论正确的是( )
(A)是偶函数,递增区间是 (B)是偶函数,递减区间是
(C)是奇函数,递减区间是 (D)是奇函数,递增区间是
【答案】C
【2012黄冈市高三上学期模拟考试理】函数,则函数的零点个数有 个。
【答案】 2
【解析】本题主要考查. 属于基础知识、基本运算的考查.
∵分别作出、的图像,知交点数即零点数为2
【2012武昌区高三年级调研理】函数的图象如图所示,给出以下说法:
①函数的定义域是[一l,5];
②函数的值域是(一∞,0]∪[2,4];
③函数在定义域内是增函数;
④函数在定义域内的导数
其中正确的是 ( )
A.①② B.①③ C.②③ D.②④
【答案】A
【解析】本题主要考查函数的图像与性质. 属于基础知识的考查.
的定义域中含有,①②正确;函数在定义域内不是增函数,因而③④错误。
【2012武昌区高三年级元月调研理】若 ( )
A. B. C. D.
【答案】D
【解析】本题主要考查对数的基本运算以及指数的运算. 属于基础知识、基本运算的考查.
由,,所以
【2012厦门模拟质检理10】已知函数f(x)=则下列结论正确的是
A.f(x)在(-1,0)上恰有一个零点 B. f(x)在(0,1)上恰有一个零点
C.f(x)在(-1,0)上恰有两个零点 D. f(x)在(0,1)上恰有两个零点
【答案】A
【解析】因为函数f(x)=在单调增,,选A;
【2012厦门模拟质检理13】定义区间[x1,x2]( x1
【答案】
【答案】B
【解析】因为奇函数在上的解析式是,取
【2012宁德质检理10】若函数在给定区间M上,存在正数t,使得对于任意,有,且,则称为M上的t级类增函数,则以下命题正确的是 ( )
A.函数上的1级类增函数
B.函数上的1级类增函数
C.若函数上的级类增函数,则实数a的最小值为2
D.若函数上的t级类增函数,则实数t的取值范围为
【答案】D
【2012深圳中学模拟理5】值域为{2,5,10},其对应关系为的函数的个数 ( )
A . 1 B. 27
C. 39 D. 8
【答案】B
【解析】解:分别由解得由函数的定义,定义域中元素的选取分四种情况:
1取三个元素:有C21种
2取四个元素:先从三组中选取一组再从剩下的两组中选两个元素,故共有种;
3取五个元素:=6种;
4取六个元素:1种。
由分类计数原理,共有8+12+6+1=27种。
【2012深圳中学模拟理6】设函数,则满足方程根的个数是( )
A.1 个 B.2 个 C.3 个 D.无数个
【答案】C
【解析】方法一:详细画出f(x)和g(x)在同一坐标系中函数图象,由图5中不难看出有三个交点,故选C
方法二:①当时,,则
②当时,,则
③当时,,则
④当时,,则
⑤当时,,则
由此下区x的解成指数增长,而区间成正比增长,故以后没有根了!所以应选C。
【2012海南嘉积中学模拟理12】规定表示两个数中的最小的数,,若函数的图像关于直线对称,则的值是( )
A、-1 B、1 C、-2 D、2
【答案】B
【解析】的图像关于直线对称,,
【2012海南嘉积中学模拟理15】若函数,若,则实数的取值范围是 .
数,当时,设函数的值域为集合,记中的元素个数为,则使为最小时的是( )
A.7 B.9 C.10 D.13
【答案】C
【解析】时,时,,;,取得最小值。
【2012浙江瑞安模拟质检理17】对于函数,若存在区间,当时的值域为,则称为倍值函数.若是倍值函数,则实数的取值范围是 .
【2012武昌区高三年级调研理】某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为,其中为销售量(单位:辆).若该公司在这两地共销售15辆车,则能获得的最大利润为 万元.
【答案】 45.6
【解析】本题主要考查函数的应用问题及二次函数的最值. 属于基础知识、基本运算的考查.
设甲地销量为辆,则乙地销量为15-辆,总利润为y(单位:万元),则
,
即 二次函数对称轴为
∵,故辆时y最大,最大值为45.6万元。
【2012黄冈市高三模拟考试理】某工厂生产一种产品的原材料费为每件40元,若用x表示该厂生产这种产品的总件数,则电力与机器保养等费用为每件0.05x元,又该厂职工工资固定支出12500元。
(1)把每件产品的成本费P(x)(元)表示成产品件数x的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量x不超过3000件,且产品能全部销售,根据市场调查:每件产品的销售价Q(x)与产品件数x有如下关系:,试问生产多少件产品,总利润最高?(总利润=总销售额-总的成本)
【解析】本题主要考查函数的应用问题、逻辑思维能力、推理论证能力.
【2012宁德质检理】(本小题满分13分)
已知函数
(1)若函数为奇函数,求实数k的值;
(2)若对任意的都有成立,求实数k的取值范围。
【2012深圳中学模拟理】(本小题满分14分)
已知集合.其中 为正常数.
(I)设,求的取值范围.
(II)求证:当时不等式对任意恒成立;
(III)求使不等式对任意恒成立的的范围.
【答案】(I),当且仅当时等号成立,
故的取值范围为.(3分)
(II) 变形,得
. (5分)
由,又,,∴在上是增函数,
所以.
即当时不等式成立. (9分)
【2012·泉州四校二次联考理】(本小题满分13分)
省环保研究所对市中心每天环境放射性污染情况进行调查研究后,发现一天中环境综合放射性污染指数与时刻(时)的关系为,
其中是与气象有关的参数,且,若用每天的最大值为当天的综合放射性污染指数,并记作.
(1)令,,求t的取值范围;
(2)省政府规定,每天的综合放射性污染指数不得超过2,试问目前市中心的综合放射性污染指数是否超标?
(本小题满分13分)
【解】(1)当时,t=0; ……………………1分
当时,(当时取等号),
∴,
【2012厦门市高三模拟理】设函数f(x)=-x3+mx2+x,g(x)=mx2-x+c,F(x)=x f(x)。
(Ⅰ) 若函数y= f(x)在x=2处有极值,求实数m的值;
(Ⅱ) 试讨论方程y=F'(x)=g(x)的实数解的个数;
(Ⅲ)记函数y= G(x)的导称函数G'( x)在区间(a,b)上的导函数为G''( x),若在(a,b)上G''( x)>0恒成立,则称函数G(x) (a,b)上为“凹函数”。若存在实数m∈[-2,2],使得函数F(x)在(a,b)上为“凹函数”,求b-a最大值。
【解析】本题主要考查函数、导数知识及其应用,考查运算求解能力及抽象概括能力,考查函数与方程、分类与整合、数形结合、化归与转化等思想方法.
(II)F'(x)=
F'(x)=g(x), 即,即
令,则
∵
∴
由图知,
当时,F'(x)=g(x)的实数解的个数为1
当时,F'(x)=g(x)的实数解的个数为2
当时,F'(x)=g(x)的实数解的个数为3
当时,F'(x)=g(x)的实数解的个数为2
的两根为,则
,m∈[-2,2]
的最大值为,故,从而b-a最大值为
(Ⅱ), , ………………8分
,
……………………10分
即: .
的取值范围………………12分
【2012武昌区高三年级调研理】已知函数为R上的奇函数,的导数为,且当时,不等式成立,若对一切恒成立,则实数的取值范围是 。
【答案】
(1)求函数的极大值点;
(2)当时,若在上至少存在一点,使成立,求的取值范围.
【解析】本题主要考查了导数的计算、导数与单调性的关系、极值问题以及恒成立问题。属于难题。考查了基础知识、基本运算、基本变换能力和转换的思想、分类讨论的思想.
由(1)知,①当,即时,
综上所述,当时,在上至少存在一点,使成立。
【2012三明市普通高中高三联考理】已知函数图象上点处的 令得 ,则此方程在上恰有两解。 ………8分
记
得 ………10分
v
的图像如图所示(或 ) ………………………13分
. ………………………14分
【2012黄冈市高三模拟考试理】已知函数
(1)曲线经过点P(1,2),且曲线C在点P处的切线平行于直线,求a,b的值;
(2)在(1)的条件下试求函数的极小值;
(3)若在区间(1,2)内存在两个极值点,求证:
【解析】本题主要考查函数、导数知识及其应用,考查运算求解能力及抽象概括能力,考查函数与方程、分类与整合、数形结合、化归与转化等思想方法.
【解】(1)=,
由题设知: 解得………………………4分
(Ⅱ)由(1)知
=mx(x-),当m>0时,g(x)在(-,0),(,+)上递增,在(0,)上递减,所以g(x)的极小值为g()=-m;当m<0时,g(x)在(-,0),(,+)上递减,在(0,)上递增,所以g(x)的极小值为g(0)=0;……8分
(Ⅲ)因为在区间内存在两个极值点,所以,
即在内有两个不等的实根.
∴ ……………………………11分
由 (1)+(3)得,由(4)得,
∴,又,∴.
故a+b的取值范围是(0,2)……………………………14分
【2012武昌区高三年级模拟理】已知函数
(Ⅰ)求函数的单调区间;
(Ⅱ)若恒成立,试确定实数k的取值范围;
(Ⅲ)证明:
而不成立,故.
当时,由(Ⅰ)知.
要使恒成立,则即可.
故,解得.
(Ⅲ)由(Ⅱ)知,当时有在恒成立,且在上是减函数,,
所以且, …………4分
(I)因为为的极大值点,所以
当时,;当时,;当时,
所以的递增区间为,;递减区间为.…………7分
(II)①若,则在上递减,在上递增
恰有两解,则,即,所以;
②若,则,
同课章节目录
