人教版数学六年级上册 第四单元 2比的基本性质 课(19页ppt)
文档属性
| 名称 | 人教版数学六年级上册 第四单元 2比的基本性质 课(19页ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 16:13:15 | ||
图片预览





文档简介
第四单元
比
比的基本性质
一、情境导入
小明、小强、小丽都喜欢制作折纸。有一天,他们三人在
争论谁每分钟折的纸鹤数多?
小明说:“我折的纸鹤数与时间(分)的比是6︰8。”
小强说:“我折的纸鹤数与时间(分)的比是3︰4。”
小丽说:“我折的纸鹤数与时间(分)的比是12︰16。”
问题:小明、小强和小丽谁折得快?
一、情境导入
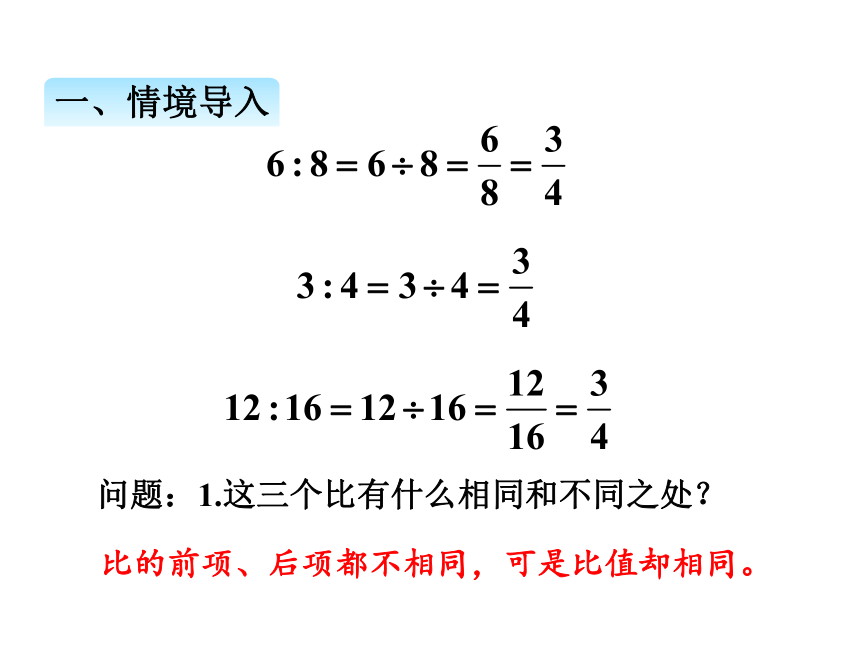
问题:1.这三个比有什么相同和不同之处?
比的前项、后项都不相同,可是比值却相同。
一、情境导入
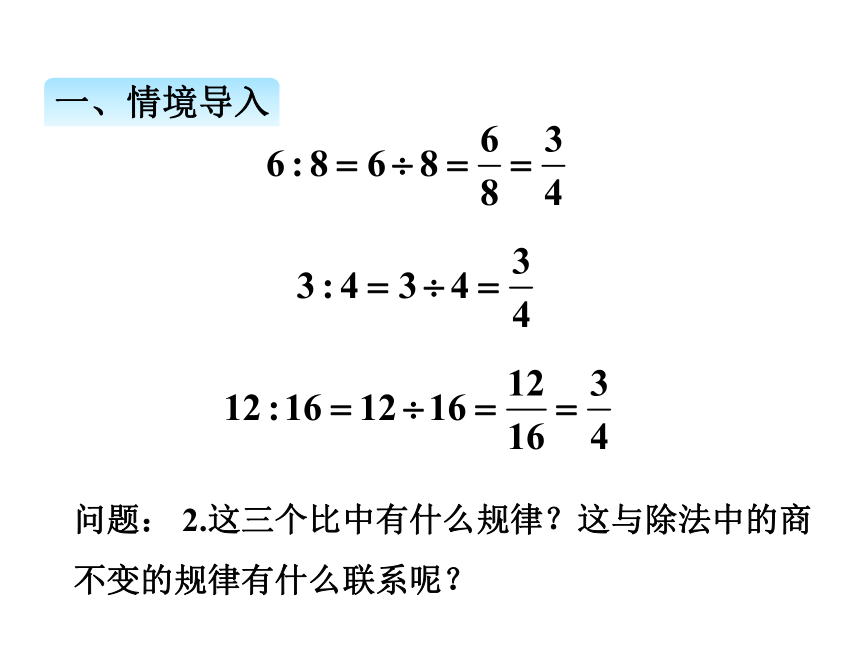
问题: 2.这三个比中有什么规律?这与除法中的商不变的规律有什么联系呢?
二、探究新知
借助商不变的规律,你发现比中有什么规律?
6÷8=(6×2)÷(8×2)=12÷16
6÷8=(6÷2)÷(8÷2)=3÷4
6︰8
6︰8
=(6×2)︰(8×2)
=12︰16
=(6÷2)︰(8÷2)
=3︰4
二、探究新知
比的前项和后项同时乘或除以相同的数(0除外),比值不变,这叫作比的基本性质。
三、解决问题
(一)明确什么是最简单的整数比
18︰27 4︰9 3︰15
4.5︰9 5︰6 7︰11
问题:哪些是整数比?哪些比的前项和后项是互质的?
前项和后项都是整数,而且又是互质数,这样的比
就叫最简单整数比。
三、解决问题
三、解决问题
(二)化简比
“神舟”五号搭载了两面联合国旗,一面长15cm,宽10cm,另一面长180cm,宽120cm。这两面联合国旗的长和宽的最简单的整数比分别是多少?
15cm
10cm
180cm
120cm
这两面联合国国旗长和宽的最简单的整数比分别是多少?
三、解决问题
三、解决问题
15︰10=(15÷5) ︰(10÷5)
=3︰2
180︰120=(180÷60)︰(120÷60)
= 3︰2
想:5是15和10的什么数?为什么要除以5?
把下面各比化成最简单的整数比。
0.75︰2
=(0.75×100)︰(2×100)
=75︰200
=3:8
想:为什么要乘18?
三、解决问题
三、解决问题
分数比
整数比
小数比
前、后项同乘
分母的最小公
倍数
前、后项的小数点
右移相同位数
最简单的整数比
前、后项同除以它们的最大公因数
化简比的方法
四、巩固练习
1.把下面各比化成最简单的整数比。
=2︰1
=6︰5
=1︰2
=5︰1
=14︰9
=1︰5
五、知识拓展
你听说过“黄金比”吗?
把一条线段分成两部分,如果较短部分与较长部分长度之比等于较长部分与整体长度之比,我们把这个比称为黄金比(约为 0.618︰1)。当一个物体的两个部分长度的比大致符合黄金比时,常常会给人以一种优美的视觉感受,所以,设计许多物品时都含有黄金比这一因素。
五、知识拓展
a:b ≈ 0.618︰1
五、知识拓展
c
c
c 和 a 也符合黄金比
六、课堂小结
这节课我们有什么收获?
说一说自己的问题是什么?
完成练习册本课时的习题。
七、课后作业
比
比的基本性质
一、情境导入
小明、小强、小丽都喜欢制作折纸。有一天,他们三人在
争论谁每分钟折的纸鹤数多?
小明说:“我折的纸鹤数与时间(分)的比是6︰8。”
小强说:“我折的纸鹤数与时间(分)的比是3︰4。”
小丽说:“我折的纸鹤数与时间(分)的比是12︰16。”
问题:小明、小强和小丽谁折得快?
一、情境导入
问题:1.这三个比有什么相同和不同之处?
比的前项、后项都不相同,可是比值却相同。
一、情境导入
问题: 2.这三个比中有什么规律?这与除法中的商不变的规律有什么联系呢?
二、探究新知
借助商不变的规律,你发现比中有什么规律?
6÷8=(6×2)÷(8×2)=12÷16
6÷8=(6÷2)÷(8÷2)=3÷4
6︰8
6︰8
=(6×2)︰(8×2)
=12︰16
=(6÷2)︰(8÷2)
=3︰4
二、探究新知
比的前项和后项同时乘或除以相同的数(0除外),比值不变,这叫作比的基本性质。
三、解决问题
(一)明确什么是最简单的整数比
18︰27 4︰9 3︰15
4.5︰9 5︰6 7︰11
问题:哪些是整数比?哪些比的前项和后项是互质的?
前项和后项都是整数,而且又是互质数,这样的比
就叫最简单整数比。
三、解决问题
三、解决问题
(二)化简比
“神舟”五号搭载了两面联合国旗,一面长15cm,宽10cm,另一面长180cm,宽120cm。这两面联合国旗的长和宽的最简单的整数比分别是多少?
15cm
10cm
180cm
120cm
这两面联合国国旗长和宽的最简单的整数比分别是多少?
三、解决问题
三、解决问题
15︰10=(15÷5) ︰(10÷5)
=3︰2
180︰120=(180÷60)︰(120÷60)
= 3︰2
想:5是15和10的什么数?为什么要除以5?
把下面各比化成最简单的整数比。
0.75︰2
=(0.75×100)︰(2×100)
=75︰200
=3:8
想:为什么要乘18?
三、解决问题
三、解决问题
分数比
整数比
小数比
前、后项同乘
分母的最小公
倍数
前、后项的小数点
右移相同位数
最简单的整数比
前、后项同除以它们的最大公因数
化简比的方法
四、巩固练习
1.把下面各比化成最简单的整数比。
=2︰1
=6︰5
=1︰2
=5︰1
=14︰9
=1︰5
五、知识拓展
你听说过“黄金比”吗?
把一条线段分成两部分,如果较短部分与较长部分长度之比等于较长部分与整体长度之比,我们把这个比称为黄金比(约为 0.618︰1)。当一个物体的两个部分长度的比大致符合黄金比时,常常会给人以一种优美的视觉感受,所以,设计许多物品时都含有黄金比这一因素。
五、知识拓展
a:b ≈ 0.618︰1
五、知识拓展
c
c
c 和 a 也符合黄金比
六、课堂小结
这节课我们有什么收获?
说一说自己的问题是什么?
完成练习册本课时的习题。
七、课后作业
