24.2.1:点和圆的位置关系 同步提高课时练习(含解析)
文档属性
| 名称 | 24.2.1:点和圆的位置关系 同步提高课时练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
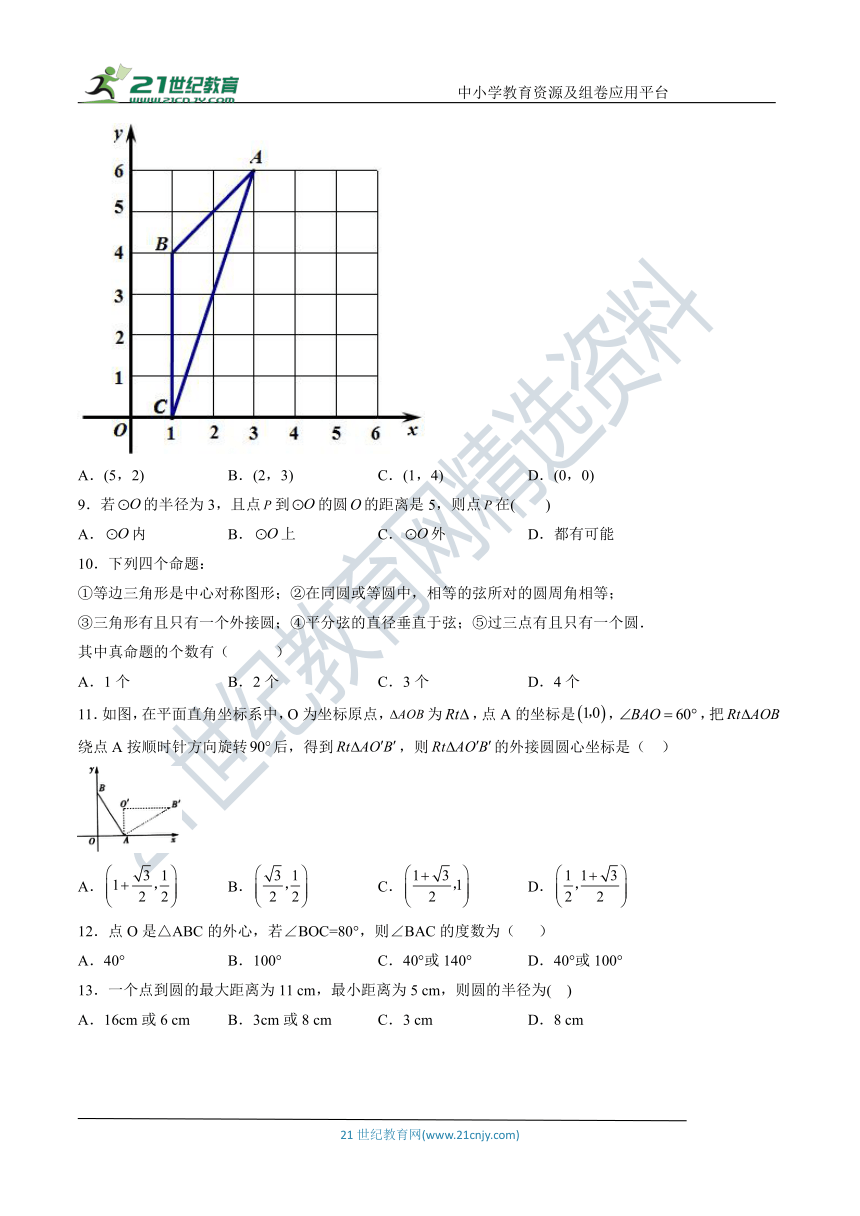
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 15:44:37 | ||
图片预览




文档简介
24.2.1:点和圆的位置关系
1.若一个三角形的外心在这个三角形的一边上,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
2.已知矩形ABCD的边AB=15,BC=20,以点B为圆心作圆,使A,C,D三点至少有一点在⊙B内,且至少有一点在⊙B外,则⊙B的半径r的取值范围是( ).
A.r>15 B.15<r<20 C.15<r<25 D.20<r<25
3.已知⊙O的半径为r=5,点P和圆心O之间的距离为d,且方程x2﹣false=0没有实数根.则点P与⊙O的位置关系是( )
A.在圆上 B.在圆内 C.在圆外 D.不能确定
4.已知点C为线段AB延长线上的一点,以A为圆心,AC长为半径作⊙A,则点B与⊙A的位置关系为( )
A.点B在⊙A上 B.点B在⊙A外 C.点B在⊙A内 D.不能确定
5.从一块圆形玻璃镜残片的边缘描出三点A、B、C,得到△ABC,则这块玻璃镜的圆心是( )
A.AB、AC边上的高所在直线的交点
B.AB、AC边的垂直平分线的交点
C.AB、AC边上的中线的交点
D.∠BAC与∠ABC的角平分线的交点
6.false中,false,false,若要剪一张圆形纸片盖住这个三角形,则圆形纸片的最小半径为( )false.
A.false B.false C.false D.false
7.用反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是( )
A.点在圆内 B.点在圆上 C.点在圆心上 D.点在圆上或圆内
8.如图,false外接圆的圆心坐标是( )
A.(5,2) B.(2,3) C.(1,4) D.(0,0)
9.若false的半径为3,且点false到false的圆false的距离是5,则点false在( )
A.false内 B.false上 C.false外 D.都有可能
10.下列四个命题:
①等边三角形是中心对称图形;②在同圆或等圆中,相等的弦所对的圆周角相等;
③三角形有且只有一个外接圆;④平分弦的直径垂直于弦;⑤过三点有且只有一个圆.
其中真命题的个数有( )
A.1个 B.2个 C.3个 D.4个
11.如图,在平面直角坐标系中,O为坐标原点,false为false,点A的坐标是false,false,把false绕点A按顺时针方向旋转false后,得到false,则false的外接圆圆心坐标是( )
A.false B.false C.false D.false
12.点O是△ABC的外心,若∠BOC=80°,则∠BAC的度数为( )
A.40° B.100° C.40°或140° D.40°或100°
13.一个点到圆的最大距离为11 cm,最小距离为5 cm,则圆的半径为( )
A.16cm或6 cm B.3cm或8 cm C.3 cm D.8 cm
14.在平面直角坐标系xOy中,如果⊙O是以原点O(0,0)为圆心,以5为半径的圆,那么点A(﹣3,﹣4)与⊙O的位置关系是( )
A.在⊙O内 B.在⊙O上 C.在⊙O外 D.不能确定
15.下列命题:(1)连接圆上两点就是弦(2)三点确定一个圆(3)一条弦所对的两条弧中必定一条是优弧,另一条是劣弧(4)正多边形既是轴对称图形,又是中心对称图形(5)任意一个三角形一定有一个外接圆并且只有一个外接圆.其中正确的个数是( )
A.0个 B.1个 C.2个 D.3个
16.如图,点O为等边三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,下列三角形中,外心不是点O的是( )
A.△CBE B.△ACD C.△ABE D.△ACE
17.过三点(2,2),(6,2),(4,5)的圆的圆心坐标为( )
A.(4,) B.(4,3) C.(5,) D.(5,3)
18.小明在学了尺规作图后,通过“三弧法”作了一个△ACD,其作法步骤是:①作线段AB,分别以A,B为圆心,AB长为半径画弧,两弧的交点为C;②以B为圆心,AB长为半径画弧交AB的延长线于点D;③连结AC,BC,CD.下列说法不正确的是( )
A.∠A=60° B.△ACD是直角三角形
C.BC=falseCD D.点B是△ACD的外心
19.已知:false,求作false的外接圆,作法:①分别作线段BC,AC的垂直平分线EF和MN,它们交于点O;②以点O为圆心,OB的长为半径画弧,如图⊙O即为所求,以上作图用到的数学依据是___________________.
20.如图,在△ABC中,AB=AC,作AD⊥BC于点D,以点A为圆心,AD为半径画⊙A.则点B与⊙A的位置关系为_____(填“在圆内”.“在圆上”或“在圆外”)
21.如图,在false中,false,false,false,false是中线,以false为圆心、false长为半径画圆,则false,false,false三点,在圆内的是点________,在圆外的是点________,在圆上的是点________.
22.在平面直角坐标系xOy中,点A(4,3)为⊙O上一点,B为⊙O内一点,请写出一个符合条件要求的点B的坐标______.
23.阅读下面材料:
在数学课上,老师提出如下问题:
已知:如图1△ABC,尺规作图:求作∠APC=∠ABC.
甲、乙两位同学的主要作法如下:
甲同学的主要作法,如图甲:①作∠CAD=∠ACB,且点D与点B在AC的异侧;②在射线AD上截取AP=CB,连结CP.所以∠APC=∠ABC.
乙同学的主要作法,如图乙:①作线段BC的垂直平分线a;②作线段AB的垂直平分线b,与直线a交于点O;③以点O为圆心,OA为半径作⊙O;④在false上取一点P(点P不与点A,B,C重合),连结AP,CP.所以∠ACP=∠ABC.
老师说:“两位同学的作法都是正确的.”
请你选择一位同学的作法,并说明这位同学作图的依据.
我选择的是_________的作法,这样作图的依据是_________.
24.已知false的面积为false,false所在的平面内有一点false,若false,则点false在________;若false,则点false在________;若false________false,则点false在false上.
25.锐角三角形的外心在______,直角三角形的外心在____ ,钝角三角形的外心在______.
26.外心在三角形的一边上的三角形是______三角形.
27.如图,在平面直角坐标系xOy中,点A,B,C的坐标分别是(0,4),(4,0),(8,0),⊙M是△ABC的外接圆,则点M的坐标为___________.
28.已知Rt△ABC中,∠C=90°,AC=3,BC=false,CD⊥AB,垂足为点D,以点D为圆心作⊙D,使得点A在⊙D外,且点B在⊙D内.设⊙D的半径为r,那么r的取值范围是_________.
29.下面是“作顶角为 120°的等腰三角形的外接圆”的尺规作图过程.已知:△ABC,AB=AC,∠A=120°.求作:△ABC 的外接圆.作法:(1)分别以点 B 和点 C 为圆心,AB 的长为半径作弧,两弧的一个交点为 O;(2)连接 BO;(3)以 O 为圆心,BO 为半径作⊙O.⊙O 即为所求作的圆.请回答:该尺规作图的依据是_______.
30.如图所示,△ABC的三个顶点的坐标分别为A(﹣1,3)、B(﹣2,﹣2)、C(4,﹣2),则△ABC外接圆半径的长度为_____.
31.如图,在false中,false,false,false,false为斜边false上的两个点,且false,false,则false的外接圆的半径是________.
32.已知⊙O的半径是一元二次方程x2+6x﹣16=0的解,且点O到直线AB的距离是false,则直线AB与⊙O的位置关系是_____.
33.在矩形ABCD中,AB=8,AD=6,以A为圆心作圆,如果B,C,D三点中至少有一点在圆内,且至少有一点在圆外,则圆A的半径r的取值范围是____________.?
34.如图,Rt△ABC中,∠ACB=90°,CD=5,D是AB的中点,则外接圆的半径r=_____.
35.如图,一条公路的转弯处是一段圆弧false.用直尺和圆规作出false所在圆的圆心O(要求保留作图痕迹,不写作法);
36.如图,方格中每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
(1)画出将△ABC绕点O逆时针方向旋转90°得到△A1B1C1,并写出点A1,B1,C1的坐标;
(2)画出△ABC的外接圆,并写出其圆心的坐标.
37.如图,矩形false中,false,false.作DE⊥AC于点E,作AF⊥BD于点F.
(1)求AF、AE的长;
(2)若以点false为圆心作圆, false、false、false、E、F五点中至少有1个点在圆内,且至少有2个点在圆外,求false的半径 false 的取值范围.
38.如图,已知△ABC内接于⊙O,AB=AC,false=100°,连结AO.
(1)求false和 false的度数;
(2)求证:AO平分∠BAC.
39.⊙O的半径r=10cm,圆心O到直线l的距离OD=6cm,在直线l上有A、B、C三点,且AD=6cm,BD=8cm,CD=5falsecm,问:A、B、C三点与⊙O的位置关系各是怎样?
40.如图,以等腰三角形false的底边false为直径的圆,与另两边false分别交于点false,请你仅用无刻度的直尺分别按下列要求画图(保留画图痕迹,不写画法)
(1)在图1中,画一条直线与false平行.
(2)在图2中,画一个以false为对角线的矩形.
41.如图,点false都在false上,请仅用无刻度的直尺分别按下列要求画图. (不写作法,保留作图痕迹)
(1)在图1中,若false,画一个false的内接等腰直角三角形.
(2)在图2中,若点false在弦false上,且false,画一个false的内接等腰直角三角形.
42.如图,⊙O是△ABC的外接圆,∠BAC与∠ABC的平分线相交于点I,延长AI交⊙O于点D,连结BD,DC.
(1)求证:BD=DC=DI;
(2)若⊙O的半径为10 cm,∠BAC=120°,求△BDC的面积.
43.如图,∠BCD=90°,BC=DC,直线PQ经过点D.设∠PDC=α(45°<α<135°),BA⊥PQ于点A,将射线CA绕点C按逆时针方向旋转90°,与直线PQ交于点E.
(1)判断:∠ABC ∠PDC(填“>”或“=”或“<”);
(2)猜想△ACE的形状,并说明理由;
(3)若△ABC的外心在其内部(不含边界),直接写出α的取值范围.
44.对于一个三角形,设其三个内角度数分别为false,false和false,若x,y,z满足false,我们定义这个三角形为美好三角形.
(1)△ABC中,若false,false,则△ABC (填”是”或”不是”)美好三角形;
(2)如图,锐角△ABC是⊙O的内接三角形,false,false,⊙O直径为false,求证:△ABC为美好三角形;
(3)已知△ABC为美好三角形,false,求false的度数.
45.如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).
(1)在图中画出经过A、B、C三点的圆弧所在圆的圆心M的位置;
(2)点M的坐标为 ;
(3)判断点D(5,﹣2)与⊙M的位置关系.
参考答案
1.B
【解析】
试题分析:锐角三角形的外心在三角形的内部,直角三角形的外心是其斜边的中点,钝角三角形的外心在其三角形的外部;由此可知若三角形的外心在它的一条边上,那么这个三角形是直角三角形.故选B.
考点:三角形的外接圆与外心.
2.C
【解析】
试题分析:要确定点与圆的位置关系,主要根据点与圆心的距离与半径的大小关系来进行判断.
当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.在直角△BCD中CD=AB=15,BC=20,则BD=false=false=25.由图可知15<r<25,故选C.
考点:1.点与圆的位置关系;2.勾股定理;3.矩形的性质.
3.C
【解析】先根据方程x2﹣false=0求得d的取值范围,再根据点与圆的位置关系即可得出结论.
【解答】解:∵方程x2﹣false=0没有实数根,
∴△=(﹣false)2﹣4×1×false<0,
∴d>5.
∵⊙O的半径为r=5,r<d,
∴点P在圆外.
故选:C.
【点评】本题考查点与圆的位置关系,熟知点与圆的三种位置关系是解题的关键.
4.C
【解析】根据题意确定AC>AB,从而确定点与圆的位置关系即可.
【解答】解:∵点C为线段AB延长线上的一点,
∴AC>AB,
∴以A为圆心,AC长为半径作⊙A,则点B与⊙A的位置关系为点B在⊙A内,
故选:C.
【点评】本题考查的知识点是点与圆的位置关系,根据题意确定出AC>AB是解此题的关键.
5.B
【解析】结合图形可知所求玻璃镜的圆心是false外接圆的圆心,据此可得出答案.
【解答】根据题意可知,所求的玻璃镜的圆心是false外接圆的圆心,而false外接圆的圆心是三边垂直平分线的交点,
故选:B.
【点评】本题主要考查三角形外接圆,掌握三角形三边垂直平分线的交点是三角形外接圆的圆心是解题的关键.
6.D
【解析】作false于false,根据等腰三角形的性质求出false,根据勾股定理求出false,设圆形纸片的半径为false,根据勾股定理列出方程,解方程得到答案.
【解答】解:如图,点点A作false于false,
false,false,false,
false,false的外接圆的圆心false在false上,
连接false,
在Rt△ABD中,false,
设圆形纸片的半径为false,
则false,
在false中,false,
则false,
解得,false,
∴此时圆形纸片的半径为falsefalse.
故选:false.
【点评】本题考查的是三角形的外接圆与外心、等腰三角形的性质,掌握等腰三角形的三线合一、三角形外接圆的性质及勾股定理是解题的关键.
7.D
【解答】【分析】在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
【解答】用反证法证明时,假设结论“点在圆外”不成立,
那么点应该在圆内或者圆上.
故选D.
【点评】考查反证法以及点和圆的位置关系,解题的关键是掌握点和圆的位置关系.
8.A
【解析】根据三角形各边的中垂线的交点为三角形外接圆的圆心,作出false外接圆的圆心,进而即可得到坐标.
【解答】如图,作AB,BC的中垂线,交于点D,点D即为false外接圆的圆心,坐标为(5,2).
故选A.
【点评】本题主要考查三角形外接圆的圆心,熟练掌握三角形外接圆的圆心是各边中垂线的交点,是解题的关键.
9.C
【解析】要确定点与圆的位置关系,主要确定点与圆心的距离与半径的大小关系,设点与圆心的距离d,则d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
【解答】解:∵点到圆心的距离5,大于圆的半径3,
∴点在圆外.故选C.
【点评】判断点与圆的位置关系,也就是比较点与圆心的距离和半径的大小关系.
10.A
【解析】根据中心对称图形的定义、圆周角的性质、三角形的外接圆、垂径定理、圆的确定依次判断即可.
【解答】①等边三角形是中心对称图形不是中心对称图形,故错误;
②在圆中一条弦所对的圆周角有两个,则在同圆或等圆中,相等的弦所对的圆周角不一定相等,故错误;
③三角形有且只有一个外接圆,故正确;
④平分弦(不是直径)的直径垂直于弦,故错误;
⑤过不在同一直线上的三点有且只有一个圆,故错误;
故是真命题的是③,
故选:A.
【点评】此题考查真命题:正确的命题是真命题,正确掌握中心对称图形的定义、圆周角的性质、三角形的外接圆、垂径定理、圆的确定是解此题的关键.
11.A
【解析】取AB'中点P,过点P分别作PE⊥x轴,根据旋转的性质可得AB=AB',∠BAB'=90°,∠B'O'A=∠BOA=90°,先说明false的外接圆圆心为点P,再利用点A的坐标是false,false,求得AB长,进而可得AB'的长,在求得∠PAE=30°,在Rt△PAE中,利用30°角的性质及勾股定理即可求得答案.
【解答】解:如图,取AB'中点P,过点P分别作PE⊥x轴,垂足为点E,连接PO',
∵把false绕点A按顺时针方向旋转false后,得到false,
∴AB=AB',∠BAB'=90°,∠B'O'A=∠BOA=90°,
∵点P为AB'的中点,
∴PA=PB'=PO'=falseAB',
∴false的外接圆圆心为点P,
∵∠BAO=60°,∠AOB=90°,
∴∠ABO=90°-∠BAO=30°,
∴OA=falseAB,
∵点A的坐标为(1,0),
∴OA=1,
∴AB'=AB=2OA=2,
∴PA=falseAB'=1,
∵∠BAB'=90°,∠BAO=60°,
∴∠PAE=180°-∠BAB'-∠BAO=30°,
∴PE=falsePA=false,
∴在Rt△PEA中,false,
∴点P的坐标为false.
【点评】本题考查了含30°角的直角三角形的性质、勾股定理,直角三角形的外接圆等相关知识,熟练掌握含30°角的直角三角形的性质及勾股定理是解决本题的关键.
12.C
【解答】试题分析:如图所示:∵O是△ABC的外心,∠BOC=80°,∴∠A=40°,∠A′=140°,
故∠BAC的度数为:40°或140°.故选C.
【考点】三角形的外接圆与外心;圆周角定理.
13.B
【解析】最大距离与最小距离的和是直径;当点P在圆外时,点到圆的最大距离与最小距离的差是直径,由此得解.
【解答】当点P在圆内时,最近点的距离为5cm,最远点的距离为11cm,则直径是16cm,因而半径是8cm;
当点P在圆外时,最近点的距离为5cm,最远点的距离为11cm,则直径是6cm,因而半径是3cm;
故选B.
【点评】本题考查了点与圆的位置关系,利用线段的和差得出直径是解题关键,分类讨论,以防遗漏.
14.B
【解析】根据两点间的距离公式求出AO的长,然后与⊙O的半径比较,即可确定点A的位置.
【解答】∵点A(﹣3,﹣4),∴AO=false=5,∵⊙O是以原点O(0,0)为圆心,以5为半径的圆,
∴点A在⊙O上,故选B.
考点:点与圆的位置关系;坐标与图形性质.
15.B
【解析】分别根据弦的定义、确定圆的条件、正多边形的性质、轴对称图形及中心对称图形的性质进行解答.
【解答】解:(1)连接圆上任意两点的线段交弦,故本小题错误;
(2)不在同一条直线上的三点确定一个圆,故本小题错误;
(3)当这条弦是直径时两条弧都是半圆,故本小题错误;
(4)正三角形是轴对称图形,但不是中心对称图形,故本小题错误;
(5)因为不在同一条直线上的三点可以确定一个圆且只有一个,所以任意一个三角形一定有一个外接圆并且只有一个外接圆,故本小题正确.
故选B.
【点评】本题考查的是圆心角、弧、弦的关系,三角形的外接圆,轴对称及中心对称图形,有一定的综合性,但难易适中.
16.B
【解答】解:如图,连接OA、OB、OD.
∵O是△ABC的外心,∴OA=OB=OC.∵四边形OCDE是正方形,∴OA=OB=OE,
∵OB=OE=OC,∴O是△CBE的外心,故A不符合题意;
∵OA=OC≠OD,∴O不是△ACD的外心,故B符合题意;
∵OA=OB=OE,∴O是△ABE的外心,故C不符合题意;
∵OA=OE=OC,∴O是△ACE的外心,故D不符合题意.
故选B.
17.A
【解析】根据题意,可知线段AB的线段垂直平分线为x=4,然后由C点的坐标可求得圆心的横坐标为x=4,然后设圆的半径为r,则根据勾股定理可求解.
【解答】设圆的半径为r,则根据勾股定理可知:
false,解得r=false,
因此圆心的纵坐标为false,
因此圆心的坐标为(4,false).
故选A
考点:1、线段垂直平分线,2、三角形的外接圆,3、勾股定理
18.C
【解析】根据等边三角形的判定和性质,直角三角形的判定和性质,三角形的外心等知识一一判断即可.
【解答】解:由作图可知:AB=BC=AC,
∴△ABC是等边三角形,
∴∠A=60°,(故A正确)
∵BA=BC=BD,
∴△ACD是直角三角形,(故B正确),点B是△ACD的外心.(故D正确);
∴tanA=false=false,
∴AC=false,
∴BC=false,(故C错误)
故选C.
【点评】本题考查作图-基本作图,等边三角形的判定和性质,直角三角形的判定和性质,三角形的外心等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
19.线段的垂直平分线的性质
【解析】利用线段垂直平分线的性质得到OA=OC=OB,然后根据点与圆的位置关系可判断点A、C在⊙O上.
【解答】解:如图,连接false,
∵点O为AC和BC的垂直平分线的交点,
∴OA=OC=OB,
∴⊙O为false的外接圆.
故答案为:线段的垂直平分线的性质.
【点评】本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.考查线段的垂直平分线的性质,确定圆的条件,掌握作图的原理是解题的关键.
20.在圆外
【解析】根据点到直线距离垂线段最短,AB>AD,即AB>r,所以点B与⊙A的位置关系在圆外.
【解答】解:∵AB=AC,作AD⊥BC,
∴AB>AD,即AB>r,
∴点B与⊙A的位置关系在圆外.
故答案为:在圆外
【点评】本题考查了点与圆的位置关系定理和勾股定理等知识点的应用,点与圆(圆的半径是r,点到圆心的距离是d)的位置关系有3种:d=r时,点在圆上;d<r点在圆内;d>r点在圆外.
21.A B M
【解析】先求出AB的长,根据直角三角形斜边上的中线等于斜边的一半,求得CM的长,再由点与圆的位置关系,确定出点A,B,M与⊙C的位置关系.
【解答】解:∵∠ACB=90°,AC=2cm,BC=4cm,∴AB=false=2false.
∵CM是中线,∴CM=falseAB=false,∴M在圆上.
∵AC=2<false,∴A在圆内.
∵BC=4>false,∴B在圆外.
故答案为A,B,M.
【点评】本题考查了点与圆的位置关系:①点P在⊙O上;②点P在⊙O内;③点P在⊙O外,及勾股定理的运用.
22.(2,2).
【解析】
【解析】连结OA,根据勾股定理可求OA,再根据点与圆的位置关系可得一个符合要求的点B的坐标.
【解答】如图,连结OA,
OA=false=5,
∵B为⊙O内一点,
∴符合要求的点B的坐标(2,2)答案不唯一.
故答案为:(2,2).
【点评】考查了点与圆的位置关系,坐标与图形性质,关键是根据勾股定理得到OA的长.
23.甲 内错角相等,两直线平行;一组对边平行且相等的四边形是平行四边形;平行四边形对角相等
【解析】甲:由内错角相等,两直线平行;一组对边平行且相等的四边形是平行四边形;平行四边形对角相等可得;
乙:由线段垂直平分线上的点到这条线段两个端点的距离相等;圆的确定;同弧所对的圆周角相等可得.
【解答】解:甲、∵∠CAD=∠ACB,
∴AD∥BC,
又∵AP=CB,
∴四边形ABCP是平行四边形,
∴∠B=∠APC,
故甲作法的依据为:内错角相等,两直线平行;一组对边平行且相等的四边形是平行四边形;平行四边形对角相等.
乙、∵a为AB的中垂线、b为BC的中垂线,且交点为O,
∴OA=OB=OC,
∴点A、B、C在以O为圆心、OA为半径的圆上,
∴∠APC=∠ABC,
故乙作法的依据是:线段垂直平分线上的点到这条线段两个端点的距离相等;圆的确定;同弧所对的圆周角相等.
故答案为:甲、内错角相等,两直线平行;一组对边平行且相等的四边形是平行四边形;平行四边形对角相等.
【点评】本题主要考查作图﹣复杂作图,熟练掌握平行四边形的判定及中垂线的性质、圆周角定理是解题的关键.
24.false外, ⊙O内, 5
【解析】
【解析】首先根据圆的面积求出圆的半径,然后由点与圆的位置关系即可求解.
【解答】因为圆的面积为25πcm2,所以圆的半径为5cm.
若OP=6.5cm,因为6.5cm>5cm,则点P在⊙O外;
若OP=4cm,因为4cm<5cm,则点P在⊙O内;
若OP=5cm,则点P在⊙O上.
故答案为⊙O外;⊙O内;5.
【点评】本题考查的是点与圆的位置关系,点与圆的位置关系有3种.设⊙O的半径为r,点P到圆心的距离OP=d,则有:①点P在圆外?d>r;②点P在圆上?d=r;③点P在圆内?d<r.
25.三角形内 斜边上 三角形外
【解析】
试题分析:三角形外接圆的圆心叫做三角形的外心.三角形外接圆的圆心也就是三角形三边垂直平分线的交点,所以锐角三角形的垂直平分线交点在三角形内,直角三角形的垂直平分线的交点在斜边上,钝角三角形的垂直平分线的交点在三角形外.
26.直角
【解析】三角形外接圆的圆心是三角形的外心,外心到三个顶点的距离相等,由此即可判断三角形的形状.
【解答】∵三角形外接圆的圆心是三角形的外心,
∴外心到三个顶点的距离相等,
∵外心在三角形的一边上,
∴外心到该边上两个端点的距离相等,
由此得到外心到三角形第三个顶点的距离等于此边的一半,
∴该三角形是直角三角形,
故答案为:直角.
【点评】此题考查三角形外心的定义,正确掌握定义并运用解题是关键.
27.(6,6)
【解析】如图:由题意可得M在AB、BC的垂直平分线上,则BN=CN;证得ON=OB+BN=6,即△OMN是等腰直角三角形,得出MN=ON=6,即可得出答案.
【解答】解:如图∵圆M是△ABC的外接圆
∴点M在AB、BC的垂直平分线上,
∴BN=CN,
∵点A,B,C的坐标分别是(0,4),(4,0),(8,0)
∴OA=OB=4,OC=8,
∴BC=4,
∴BN=2,
∴ON=OB+BN=6,
∵∠AOB=90°,
∴△AOB是等腰直角三角形,
∵OM⊥AB,
∴∠MON=45°,
∴△OMN是等腰直角三角形,
∴MN=ON=6,点M的坐标为(6,6).
故答案为(6,6).
【点评】本题考查了三角形的外接圆与外心、坐标与图形性质、等腰直角三角形的判定与性质等知识,其中判定△OMN为等腰直角三角形是解答本题的关键.
28.false.
【解析】先根据勾股定理求出AB的长,进而得出CD的长,由点与圆的位置关系即可得出结论.
【解答】解:∵Rt△ABC中,∠ACB=90,AC=3,BC=false,
∴AB=false=4.
∵CD⊥AB,
∴CD=false.
∵AD?BD=CD2,
设AD=x,BD=4-x.
解得x=false,
∴点A在圆外,点B在圆内,
r的范围是false,
故答案为false.
【点评】本题考查的是点与圆的位置关系,熟知点与圆的三种位置关系是解答此题的关键.
29.该尺规作图的依据为:四边相等的四边形是菱形、有一个角为 60°的等腰三角形是等边三角形、圆的定义.
【解析】
【解析】由作图知AB=OB=OC=AC可判定四边形ABOC为菱形,根据∠BAC=120°知∠BAO=∠CAO=60°,从而得∠BAO=∠CAO=60°,即△OAB、△OAC为等边三角形,继而由OB=OA=OC可得所求作的圆.
【解答】如图,连接OA、OC,
由作图知BA=BO、OC=OA,
∵AB=AC,
∴AB=OB=OC=AC,
∴四边形ABOC为菱形(四边形相等的四边形是菱形),
又∵∠BAC=120°,
∴∠BAO=∠CAO=60°,
则△OAB、△OAC为等边三角形(有一个角为60°的等腰三角形是等边三角形),
∴OB=OA=OC,
∴点A、B、C在以O为圆心、OB为半径的圆上(圆的定义),
综上,该尺规作图的依据为:四边形相等的四边形是菱形、有一个角为60°的等腰三角形是等边三角形、圆的定义.
【点评】本题主要考查作图-复杂作图,解题的关键是熟练掌握菱形的判定与性质、等边三角形的判定与性质及圆的定义.
30.false
【解析】根据三角形的外心是三边中垂线的交点,由B、C的坐标可知,圆心M必在直线x=1上;由图知:AC的垂直平分线正好经过(1,0),由此可得到M(1,0);连接MB,过M作MD⊥BC于D,由勾股定理即可求得 M的半径长.
【解答】设△ABC的外心为M;
∵B(?2,?2),C(4,?2),
∴M必在直线x=1上,
由图知:AC的垂直平分线过(1,0),
故M(1,0);
过M作MD⊥BC于D,连接MB,
Rt△MBD中,MD=2,BD=3,
由勾股定理得:MB=false=false,
即△ABC的外接圆半径为false.
故答案为false.
【点评】本题考查了三角形的外接圆与外心与坐标与图形性质,解题的关键是熟练的掌握三角形的外接圆与外心与坐标与图形性质.
31.false
【解析】设∠DCE=x,∠ACD=y,根据等腰三角形的性质求出∠ACE、∠BDC,根据三角形内角和定理求出∠DCE=45°,根据三角形的外接圆和外心的概念求出答案.
【解答】
设∠DCE=x,∠ACD=y,则∠ACE=x+y,∠BCE=90°?∠ACE=90°?x?y,
∵AE=AC,
∴∠ACE=∠AEC=x+y,
∵BD=BC,
∴∠BDC=∠BCD=∠BCE+∠DCE=90°?x?y+x=90°?y,
在△DCE中,∵∠DCE+∠CDE+∠DEC=180°,
∴x+(90°?y)+(x+y)=180°,
解得x=45°,
∴∠DCE=45°,
∵AC=6,BC=8,
∴AB=false =10,
∵AE=AC=6,BD=BC=8,
∴DE=4,又∠DCE=45°,
如图,作直径CH,连接HE,
∴∠CEH=90°,又∠CHE=∠DCE=45°,CE=4,
∴CH=4false,
即△DCE的外接圆的直径4false,
∴△DCE的外接圆的半径为2false.
【点评】本题考查了三角形的外接圆与外心相关知识点,解题的关键是熟练的掌握三角形的外接圆与外心的性质.
32.相交
【解析】首先求出方程的根,即可得到半径长度,再比较半径与false的大小关系即可判断直线AB与⊙O的位置关系.
【解答】解:∵⊙O的半径是一元二次方程x2+6x﹣16=0的解,
解方程x2+6x﹣16=0,
(x+8)(x﹣2)=0,
解得:x1=﹣8(舍去),x2=2,
∴r=2,
∵点O到直线AB距离d是false,
∴d<r,
∴直线AB与圆相交.
故答案为:相交.
【点评】本题考查解一元二次方程,点与圆的位置关系. 点O到直线AB的距离为d,若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.
33.6【解析】
如图,连接AC,∵?在矩形ABCD中,AB=8,AD=6,∠ABC=90°,
∴AC=false=false=false=10,
∴AD∵B,C,D三点中至少有一点在⊙A内,且至少有一点⊙A在外,
∴点D一定在⊙A内,点C一定在⊙A外,
∴⊙A半径r的取值范围应大于AD的长,小于对角线AC的长,即6故答案为:6点睛:要确定点与圆的位置关系,就要确定点到圆心的距离与半径的大小关系,设点与圆心的距离d,圆的半径为r,则d>r时,点在圆外;当d=r时,点在圆上;当d34.5
【解析】首先利用直角三角形斜边上的中线等于斜边的一半的性质求出斜边AB的长,再利用直角三角形外心的位置特征得到斜边AB的长即为外接圆的直径,从而求出半径r.
【解答】解:在Rt△ABC中,∠ACB=90°,CD=5,D是AB的中点,
∴AB=2CD=10,
∵直角三角形的外心在斜边中点,
∴斜边AB即是△ABC外接圆的直径,
∴外接圆的半径r=5.
故答案为:5.
【点评】本题考查了直角三角形斜边中线等于斜边的一半的性质和直角三角形外心的位置特征,熟练掌握这些性质是解题的关键.
35.见解析.
【解析】根据垂径定理的推论可知:弦的垂直平分线过圆心,只需连接AC、BC,尺规作线段AC和BC的垂直平分线,其交点即为所求.
【解答】解:如图所示:
圆心O即为圆弧所在圆的圆心.
【点评】本题考查了尺规作线段的垂直平分线和垂径定理,属于基础题型,熟练掌握垂径定理和线段垂直平分线的尺规作图是关键.
36.(1)A1(0,﹣4),B1(3,﹣3),C1(3,﹣1);(2)(﹣2,﹣1)
【解析】(1)旋转以后易发现点A1,B1,C1的坐标;
(2)三角形外接圆的圆心为三角形各边垂直平分线的交点.
【解答】解:(1)△A1B1C1如图所示.A1(0,﹣4),B1(3,﹣3),C1(3,﹣1).
(2)△ABC的外接圆如图所示,
圆心O′的坐标为(﹣2,﹣1).
【点评】此题考查的是旋转和外接圆的圆心确定方法.
37.(1)false,false;(2)false
【解析】(1)先利用等面积法算出AF=false,再根据勾股定理得出false;
(2)根据题意点F只能在圆内,点C、D只能在圆外,所以⊙A的半径r的取值范围为false.
【解答】解:如图,
(1)在矩形false中,false,false.
∴DC=AB=3,AC=BD=false=5,
∵DE⊥AC,AF⊥BD,
∴false ;
∴AF=false,
同理,DE=false,
在Rt△ADE中,AE=false =false,
(2) 若以点false为圆心作圆, false、false、false、E、F五点中至少有1个点在圆内,则r>2.4,
当至少有2个点在圆外,r<4,
故⊙A的半径r的取值范围为:false
38.(1)130°,130°;(2)详见解析.
【解析】(1)由AB=AC,得到false=false,于是得到结论;
(2)连接OB,OC,由线段的垂直平分线的判定定理可得AD垂直平分BC,再由等腰三角形的三线合一性质可证得结论;
【解答】解:(1)∵AB=AC,
∴false=false,
∵false的度数=100°,
∴false和 false的度数=false=130°;
(2)证明:如图,连接OB,OC,延长AO交BC于D,
∵AB=AC,OB=OC,
∴点A和点O都在线段BC的垂直平分线上,
∴BD=CD,AD⊥BC,
∴∠BAD=∠CAD,
即AO平分∠BAC.
【点评】本题考查了三角形的外接圆与外心、线段垂直平分线的判定与性质、勾股定理等知识点,熟练掌握相关性质定理及其应用,是解题的关键.
39.点A在⊙O内,点B在⊙O上,点C在⊙O 外.
【解析】分别求出false、false、false三点到点false的距离,然后与圆的半径即可求得三点与圆的位置关系.
【解答】∵OA=== (cm)<r=10 cm,
OB===10(cm)=r,
OC=== (cm)>r=10 cm,
∴点A在⊙O内,点B在⊙O上,点C在⊙O 外.
【点评】本题考查了点与圆的位置关系,解题的关键是求得点与圆心的距离.
40.(1)见解析;(2)见解析
【解析】(1)结合圆内接四边形的性质和等腰三角形的性质,可知DE∥AB;
(2)结合圆周角定理及等腰三角形的性质和矩形的判定,可知四边形ADBF即为所求作.
【解答】(1)连接DE,DE即为所求;
(2)连接BD,AE相交于点M,连接CM并延长交AB于点O,连接DO并延长交圆于点N,连接AN,BN,四边形ADBN即为所求.
【点评】本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
41.(1)见解析;(2)见解析
【解析】根据内接三角形和等腰直角三角形的性质,结合题意即可得出答案.
【解答】解:(1)如图1,false即为所求(画法不唯一).
(2)如图2,false即为所求(画法不唯一)
【点评】本题主要考查了圆内接等腰直角三角形的作图方法,考查了学生的作图能力.
42.(1)见解析; (2) S△BOC75falsecm2.
【解析】(1)根据AI和BI分别是∠BAC和∠ABC的平分线来证明BD=CD,再证明∠ABI=∠CBI,∠DBC=∠BAD,求得∠DBI=∠DIB.即可;
(2)先求出∠BAD=∠CAD=∠BCD=60°.,证明△DBC是等边三角形,再求出BD即可.
【解答】(1)∵AI和BI分别是∠BAC和∠ABC的平分线,∴∠BAD=∠CAD,∠ABI=∠CBI.∴BD=CD,∠DBC=∠CAD=∠BAD.∵∠DBI=∠DBC+∠CBI.∠DIB=∠ABI+∠BAD.又∵∠ABI=∠CBI,∠DBC=∠BAD,∴∠DBI=∠DIB.∴BD=DI.∴DB=DC=DI (2)∵∠BAC=120°,∴∠BAD=∠CAD=∠BCD=60°.∵BD=DC,∴△DBC是等边三角形.∵⊙O的半径为10 cm,即BO=DO=CO=10 cm,∴BD=10false cm.∴S△BOC=false×(10false)2=75false (cm2)
【点评】本题考查的是三角形,熟练掌握熟练掌握三角形的外接圆是解题的关键.
43.(1)=;(2)△ACE是等腰直角三角形,理由见解析;(3)45°<α<90°
【解析】(1)利用四边形内角和等于360度得:∠B+∠ADC=180°,而∠ADC+∠EDC=180°,即可求解;
(2)证明△ABC≌△EDC(AAS)即可推知△ACE是等腰直角三角形;
(3)当∠ABC=α=90°时,△ABC的外心在其直角边上,∠ABC=α>90°时,△ABC的外心在其外部,即可求解.
【解答】解:(1)在四边形BADC中,∠B+∠ADC=360°﹣∠BAD﹣∠DCB=180°,
而∠ADC+∠EDC=180°,
∴∠ABC=∠PDC.
故答案是:=;
(2)△ACE是等腰直角三角形,理由如下:
∵∠ECD+∠DCA=90°,∠DCA+∠ACB=90°,
∴∠ACB=∠ECD.
由(1)知:∠ABC=∠PDC,
又∵BC=DC,
∴△ABC≌△EDC(AAS),
∴AC=CE.
又∵∠ACE=90°,
∴△ACE是等腰直角三角形;
(3)当∠ABC=α=90°时,△ABC的外心在其直角边上,
∠ABC=α>90°时,△ABC的外心在其外部,
而45°<α<135°,
故:45°<α<90°.
【点评】本题考查的是圆的综合运用,涉及到三角形全等、三角形外心等基本知识,难度不大.
44.(1)不是;(2)见解析;(3)∠C=78°或72°
【解析】(1)利用美好三角形的定义得出△ABC的形状进而求出即可;
(2)利用勾股定理的逆定理得出△ABC的形状进而得出答案;
(3)利用美好三角形的定义进而分别得出∠C的度数.
【解答】(1)解:∵△ABC中,∠A=40°,∠B=80°,
∴∠C=60°
∵402+602≠802,
∴△ABC不是美好三角形;
故答案为:不是;
(2)证明:连接OA、OC,
∵AC=2,OA=OC=false,
∴△OAC是直角三角形,即∠AOC=90°,
∴∠B=45°,
∵∠C=60°,
∴∠A=75°,
∵即三个内角满足关系:452+602=5625=752,
∴△ABC是美好三角形;
(3)解:设∠C=x°,则∠B=(150﹣x)°,
若∠C为最大角,则x2=(150﹣x)2+302,
解得x=78,
若∠B最大角,则(150﹣x)2=x2+302,
解得x=72,
综上可知,∠C=78°或72°
【点评】本题考查圆周角定理及其推论、三角形的外接圆与外心和解直角三角形,解题的关键是掌握圆周角定理及其推论、三角形的外接圆与外心和解直角三角形.
45.(1)见解析;(2)(2,0);(3)点D在⊙M内;
【解答】试题分析:(1)由网格容易得出AB的垂直平分线和BC的垂直平分线,它们的交点即为点M;
(2)根据图形即可得出点M的坐标;
(3)用两点间距离公式求出圆的半径和线段DM的长,当DM小于圆的半径时点D在圆内.
试题解析:解:(1)如图1,点M就是要找的圆心;
(2)圆心M的坐标为(2,0).故答案为(2,0);
(3)圆的半径AM=false=false.
线段MD=false=false<false,所以点D在⊙M内.
点睛:本题考查的是点与圆的位置关系,坐标与图形性质以及垂径定理,利用网格结构得到圆心M的坐标是解题的关键.
1.若一个三角形的外心在这个三角形的一边上,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
2.已知矩形ABCD的边AB=15,BC=20,以点B为圆心作圆,使A,C,D三点至少有一点在⊙B内,且至少有一点在⊙B外,则⊙B的半径r的取值范围是( ).
A.r>15 B.15<r<20 C.15<r<25 D.20<r<25
3.已知⊙O的半径为r=5,点P和圆心O之间的距离为d,且方程x2﹣false=0没有实数根.则点P与⊙O的位置关系是( )
A.在圆上 B.在圆内 C.在圆外 D.不能确定
4.已知点C为线段AB延长线上的一点,以A为圆心,AC长为半径作⊙A,则点B与⊙A的位置关系为( )
A.点B在⊙A上 B.点B在⊙A外 C.点B在⊙A内 D.不能确定
5.从一块圆形玻璃镜残片的边缘描出三点A、B、C,得到△ABC,则这块玻璃镜的圆心是( )
A.AB、AC边上的高所在直线的交点
B.AB、AC边的垂直平分线的交点
C.AB、AC边上的中线的交点
D.∠BAC与∠ABC的角平分线的交点
6.false中,false,false,若要剪一张圆形纸片盖住这个三角形,则圆形纸片的最小半径为( )false.
A.false B.false C.false D.false
7.用反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是( )
A.点在圆内 B.点在圆上 C.点在圆心上 D.点在圆上或圆内
8.如图,false外接圆的圆心坐标是( )
A.(5,2) B.(2,3) C.(1,4) D.(0,0)
9.若false的半径为3,且点false到false的圆false的距离是5,则点false在( )
A.false内 B.false上 C.false外 D.都有可能
10.下列四个命题:
①等边三角形是中心对称图形;②在同圆或等圆中,相等的弦所对的圆周角相等;
③三角形有且只有一个外接圆;④平分弦的直径垂直于弦;⑤过三点有且只有一个圆.
其中真命题的个数有( )
A.1个 B.2个 C.3个 D.4个
11.如图,在平面直角坐标系中,O为坐标原点,false为false,点A的坐标是false,false,把false绕点A按顺时针方向旋转false后,得到false,则false的外接圆圆心坐标是( )
A.false B.false C.false D.false
12.点O是△ABC的外心,若∠BOC=80°,则∠BAC的度数为( )
A.40° B.100° C.40°或140° D.40°或100°
13.一个点到圆的最大距离为11 cm,最小距离为5 cm,则圆的半径为( )
A.16cm或6 cm B.3cm或8 cm C.3 cm D.8 cm
14.在平面直角坐标系xOy中,如果⊙O是以原点O(0,0)为圆心,以5为半径的圆,那么点A(﹣3,﹣4)与⊙O的位置关系是( )
A.在⊙O内 B.在⊙O上 C.在⊙O外 D.不能确定
15.下列命题:(1)连接圆上两点就是弦(2)三点确定一个圆(3)一条弦所对的两条弧中必定一条是优弧,另一条是劣弧(4)正多边形既是轴对称图形,又是中心对称图形(5)任意一个三角形一定有一个外接圆并且只有一个外接圆.其中正确的个数是( )
A.0个 B.1个 C.2个 D.3个
16.如图,点O为等边三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,下列三角形中,外心不是点O的是( )
A.△CBE B.△ACD C.△ABE D.△ACE
17.过三点(2,2),(6,2),(4,5)的圆的圆心坐标为( )
A.(4,) B.(4,3) C.(5,) D.(5,3)
18.小明在学了尺规作图后,通过“三弧法”作了一个△ACD,其作法步骤是:①作线段AB,分别以A,B为圆心,AB长为半径画弧,两弧的交点为C;②以B为圆心,AB长为半径画弧交AB的延长线于点D;③连结AC,BC,CD.下列说法不正确的是( )
A.∠A=60° B.△ACD是直角三角形
C.BC=falseCD D.点B是△ACD的外心
19.已知:false,求作false的外接圆,作法:①分别作线段BC,AC的垂直平分线EF和MN,它们交于点O;②以点O为圆心,OB的长为半径画弧,如图⊙O即为所求,以上作图用到的数学依据是___________________.
20.如图,在△ABC中,AB=AC,作AD⊥BC于点D,以点A为圆心,AD为半径画⊙A.则点B与⊙A的位置关系为_____(填“在圆内”.“在圆上”或“在圆外”)
21.如图,在false中,false,false,false,false是中线,以false为圆心、false长为半径画圆,则false,false,false三点,在圆内的是点________,在圆外的是点________,在圆上的是点________.
22.在平面直角坐标系xOy中,点A(4,3)为⊙O上一点,B为⊙O内一点,请写出一个符合条件要求的点B的坐标______.
23.阅读下面材料:
在数学课上,老师提出如下问题:
已知:如图1△ABC,尺规作图:求作∠APC=∠ABC.
甲、乙两位同学的主要作法如下:
甲同学的主要作法,如图甲:①作∠CAD=∠ACB,且点D与点B在AC的异侧;②在射线AD上截取AP=CB,连结CP.所以∠APC=∠ABC.
乙同学的主要作法,如图乙:①作线段BC的垂直平分线a;②作线段AB的垂直平分线b,与直线a交于点O;③以点O为圆心,OA为半径作⊙O;④在false上取一点P(点P不与点A,B,C重合),连结AP,CP.所以∠ACP=∠ABC.
老师说:“两位同学的作法都是正确的.”
请你选择一位同学的作法,并说明这位同学作图的依据.
我选择的是_________的作法,这样作图的依据是_________.
24.已知false的面积为false,false所在的平面内有一点false,若false,则点false在________;若false,则点false在________;若false________false,则点false在false上.
25.锐角三角形的外心在______,直角三角形的外心在____ ,钝角三角形的外心在______.
26.外心在三角形的一边上的三角形是______三角形.
27.如图,在平面直角坐标系xOy中,点A,B,C的坐标分别是(0,4),(4,0),(8,0),⊙M是△ABC的外接圆,则点M的坐标为___________.
28.已知Rt△ABC中,∠C=90°,AC=3,BC=false,CD⊥AB,垂足为点D,以点D为圆心作⊙D,使得点A在⊙D外,且点B在⊙D内.设⊙D的半径为r,那么r的取值范围是_________.
29.下面是“作顶角为 120°的等腰三角形的外接圆”的尺规作图过程.已知:△ABC,AB=AC,∠A=120°.求作:△ABC 的外接圆.作法:(1)分别以点 B 和点 C 为圆心,AB 的长为半径作弧,两弧的一个交点为 O;(2)连接 BO;(3)以 O 为圆心,BO 为半径作⊙O.⊙O 即为所求作的圆.请回答:该尺规作图的依据是_______.
30.如图所示,△ABC的三个顶点的坐标分别为A(﹣1,3)、B(﹣2,﹣2)、C(4,﹣2),则△ABC外接圆半径的长度为_____.
31.如图,在false中,false,false,false,false为斜边false上的两个点,且false,false,则false的外接圆的半径是________.
32.已知⊙O的半径是一元二次方程x2+6x﹣16=0的解,且点O到直线AB的距离是false,则直线AB与⊙O的位置关系是_____.
33.在矩形ABCD中,AB=8,AD=6,以A为圆心作圆,如果B,C,D三点中至少有一点在圆内,且至少有一点在圆外,则圆A的半径r的取值范围是____________.?
34.如图,Rt△ABC中,∠ACB=90°,CD=5,D是AB的中点,则外接圆的半径r=_____.
35.如图,一条公路的转弯处是一段圆弧false.用直尺和圆规作出false所在圆的圆心O(要求保留作图痕迹,不写作法);
36.如图,方格中每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
(1)画出将△ABC绕点O逆时针方向旋转90°得到△A1B1C1,并写出点A1,B1,C1的坐标;
(2)画出△ABC的外接圆,并写出其圆心的坐标.
37.如图,矩形false中,false,false.作DE⊥AC于点E,作AF⊥BD于点F.
(1)求AF、AE的长;
(2)若以点false为圆心作圆, false、false、false、E、F五点中至少有1个点在圆内,且至少有2个点在圆外,求false的半径 false 的取值范围.
38.如图,已知△ABC内接于⊙O,AB=AC,false=100°,连结AO.
(1)求false和 false的度数;
(2)求证:AO平分∠BAC.
39.⊙O的半径r=10cm,圆心O到直线l的距离OD=6cm,在直线l上有A、B、C三点,且AD=6cm,BD=8cm,CD=5falsecm,问:A、B、C三点与⊙O的位置关系各是怎样?
40.如图,以等腰三角形false的底边false为直径的圆,与另两边false分别交于点false,请你仅用无刻度的直尺分别按下列要求画图(保留画图痕迹,不写画法)
(1)在图1中,画一条直线与false平行.
(2)在图2中,画一个以false为对角线的矩形.
41.如图,点false都在false上,请仅用无刻度的直尺分别按下列要求画图. (不写作法,保留作图痕迹)
(1)在图1中,若false,画一个false的内接等腰直角三角形.
(2)在图2中,若点false在弦false上,且false,画一个false的内接等腰直角三角形.
42.如图,⊙O是△ABC的外接圆,∠BAC与∠ABC的平分线相交于点I,延长AI交⊙O于点D,连结BD,DC.
(1)求证:BD=DC=DI;
(2)若⊙O的半径为10 cm,∠BAC=120°,求△BDC的面积.
43.如图,∠BCD=90°,BC=DC,直线PQ经过点D.设∠PDC=α(45°<α<135°),BA⊥PQ于点A,将射线CA绕点C按逆时针方向旋转90°,与直线PQ交于点E.
(1)判断:∠ABC ∠PDC(填“>”或“=”或“<”);
(2)猜想△ACE的形状,并说明理由;
(3)若△ABC的外心在其内部(不含边界),直接写出α的取值范围.
44.对于一个三角形,设其三个内角度数分别为false,false和false,若x,y,z满足false,我们定义这个三角形为美好三角形.
(1)△ABC中,若false,false,则△ABC (填”是”或”不是”)美好三角形;
(2)如图,锐角△ABC是⊙O的内接三角形,false,false,⊙O直径为false,求证:△ABC为美好三角形;
(3)已知△ABC为美好三角形,false,求false的度数.
45.如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).
(1)在图中画出经过A、B、C三点的圆弧所在圆的圆心M的位置;
(2)点M的坐标为 ;
(3)判断点D(5,﹣2)与⊙M的位置关系.
参考答案
1.B
【解析】
试题分析:锐角三角形的外心在三角形的内部,直角三角形的外心是其斜边的中点,钝角三角形的外心在其三角形的外部;由此可知若三角形的外心在它的一条边上,那么这个三角形是直角三角形.故选B.
考点:三角形的外接圆与外心.
2.C
【解析】
试题分析:要确定点与圆的位置关系,主要根据点与圆心的距离与半径的大小关系来进行判断.
当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.在直角△BCD中CD=AB=15,BC=20,则BD=false=false=25.由图可知15<r<25,故选C.
考点:1.点与圆的位置关系;2.勾股定理;3.矩形的性质.
3.C
【解析】先根据方程x2﹣false=0求得d的取值范围,再根据点与圆的位置关系即可得出结论.
【解答】解:∵方程x2﹣false=0没有实数根,
∴△=(﹣false)2﹣4×1×false<0,
∴d>5.
∵⊙O的半径为r=5,r<d,
∴点P在圆外.
故选:C.
【点评】本题考查点与圆的位置关系,熟知点与圆的三种位置关系是解题的关键.
4.C
【解析】根据题意确定AC>AB,从而确定点与圆的位置关系即可.
【解答】解:∵点C为线段AB延长线上的一点,
∴AC>AB,
∴以A为圆心,AC长为半径作⊙A,则点B与⊙A的位置关系为点B在⊙A内,
故选:C.
【点评】本题考查的知识点是点与圆的位置关系,根据题意确定出AC>AB是解此题的关键.
5.B
【解析】结合图形可知所求玻璃镜的圆心是false外接圆的圆心,据此可得出答案.
【解答】根据题意可知,所求的玻璃镜的圆心是false外接圆的圆心,而false外接圆的圆心是三边垂直平分线的交点,
故选:B.
【点评】本题主要考查三角形外接圆,掌握三角形三边垂直平分线的交点是三角形外接圆的圆心是解题的关键.
6.D
【解析】作false于false,根据等腰三角形的性质求出false,根据勾股定理求出false,设圆形纸片的半径为false,根据勾股定理列出方程,解方程得到答案.
【解答】解:如图,点点A作false于false,
false,false,false,
false,false的外接圆的圆心false在false上,
连接false,
在Rt△ABD中,false,
设圆形纸片的半径为false,
则false,
在false中,false,
则false,
解得,false,
∴此时圆形纸片的半径为falsefalse.
故选:false.
【点评】本题考查的是三角形的外接圆与外心、等腰三角形的性质,掌握等腰三角形的三线合一、三角形外接圆的性质及勾股定理是解题的关键.
7.D
【解答】【分析】在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
【解答】用反证法证明时,假设结论“点在圆外”不成立,
那么点应该在圆内或者圆上.
故选D.
【点评】考查反证法以及点和圆的位置关系,解题的关键是掌握点和圆的位置关系.
8.A
【解析】根据三角形各边的中垂线的交点为三角形外接圆的圆心,作出false外接圆的圆心,进而即可得到坐标.
【解答】如图,作AB,BC的中垂线,交于点D,点D即为false外接圆的圆心,坐标为(5,2).
故选A.
【点评】本题主要考查三角形外接圆的圆心,熟练掌握三角形外接圆的圆心是各边中垂线的交点,是解题的关键.
9.C
【解析】要确定点与圆的位置关系,主要确定点与圆心的距离与半径的大小关系,设点与圆心的距离d,则d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
【解答】解:∵点到圆心的距离5,大于圆的半径3,
∴点在圆外.故选C.
【点评】判断点与圆的位置关系,也就是比较点与圆心的距离和半径的大小关系.
10.A
【解析】根据中心对称图形的定义、圆周角的性质、三角形的外接圆、垂径定理、圆的确定依次判断即可.
【解答】①等边三角形是中心对称图形不是中心对称图形,故错误;
②在圆中一条弦所对的圆周角有两个,则在同圆或等圆中,相等的弦所对的圆周角不一定相等,故错误;
③三角形有且只有一个外接圆,故正确;
④平分弦(不是直径)的直径垂直于弦,故错误;
⑤过不在同一直线上的三点有且只有一个圆,故错误;
故是真命题的是③,
故选:A.
【点评】此题考查真命题:正确的命题是真命题,正确掌握中心对称图形的定义、圆周角的性质、三角形的外接圆、垂径定理、圆的确定是解此题的关键.
11.A
【解析】取AB'中点P,过点P分别作PE⊥x轴,根据旋转的性质可得AB=AB',∠BAB'=90°,∠B'O'A=∠BOA=90°,先说明false的外接圆圆心为点P,再利用点A的坐标是false,false,求得AB长,进而可得AB'的长,在求得∠PAE=30°,在Rt△PAE中,利用30°角的性质及勾股定理即可求得答案.
【解答】解:如图,取AB'中点P,过点P分别作PE⊥x轴,垂足为点E,连接PO',
∵把false绕点A按顺时针方向旋转false后,得到false,
∴AB=AB',∠BAB'=90°,∠B'O'A=∠BOA=90°,
∵点P为AB'的中点,
∴PA=PB'=PO'=falseAB',
∴false的外接圆圆心为点P,
∵∠BAO=60°,∠AOB=90°,
∴∠ABO=90°-∠BAO=30°,
∴OA=falseAB,
∵点A的坐标为(1,0),
∴OA=1,
∴AB'=AB=2OA=2,
∴PA=falseAB'=1,
∵∠BAB'=90°,∠BAO=60°,
∴∠PAE=180°-∠BAB'-∠BAO=30°,
∴PE=falsePA=false,
∴在Rt△PEA中,false,
∴点P的坐标为false.
【点评】本题考查了含30°角的直角三角形的性质、勾股定理,直角三角形的外接圆等相关知识,熟练掌握含30°角的直角三角形的性质及勾股定理是解决本题的关键.
12.C
【解答】试题分析:如图所示:∵O是△ABC的外心,∠BOC=80°,∴∠A=40°,∠A′=140°,
故∠BAC的度数为:40°或140°.故选C.
【考点】三角形的外接圆与外心;圆周角定理.
13.B
【解析】最大距离与最小距离的和是直径;当点P在圆外时,点到圆的最大距离与最小距离的差是直径,由此得解.
【解答】当点P在圆内时,最近点的距离为5cm,最远点的距离为11cm,则直径是16cm,因而半径是8cm;
当点P在圆外时,最近点的距离为5cm,最远点的距离为11cm,则直径是6cm,因而半径是3cm;
故选B.
【点评】本题考查了点与圆的位置关系,利用线段的和差得出直径是解题关键,分类讨论,以防遗漏.
14.B
【解析】根据两点间的距离公式求出AO的长,然后与⊙O的半径比较,即可确定点A的位置.
【解答】∵点A(﹣3,﹣4),∴AO=false=5,∵⊙O是以原点O(0,0)为圆心,以5为半径的圆,
∴点A在⊙O上,故选B.
考点:点与圆的位置关系;坐标与图形性质.
15.B
【解析】分别根据弦的定义、确定圆的条件、正多边形的性质、轴对称图形及中心对称图形的性质进行解答.
【解答】解:(1)连接圆上任意两点的线段交弦,故本小题错误;
(2)不在同一条直线上的三点确定一个圆,故本小题错误;
(3)当这条弦是直径时两条弧都是半圆,故本小题错误;
(4)正三角形是轴对称图形,但不是中心对称图形,故本小题错误;
(5)因为不在同一条直线上的三点可以确定一个圆且只有一个,所以任意一个三角形一定有一个外接圆并且只有一个外接圆,故本小题正确.
故选B.
【点评】本题考查的是圆心角、弧、弦的关系,三角形的外接圆,轴对称及中心对称图形,有一定的综合性,但难易适中.
16.B
【解答】解:如图,连接OA、OB、OD.
∵O是△ABC的外心,∴OA=OB=OC.∵四边形OCDE是正方形,∴OA=OB=OE,
∵OB=OE=OC,∴O是△CBE的外心,故A不符合题意;
∵OA=OC≠OD,∴O不是△ACD的外心,故B符合题意;
∵OA=OB=OE,∴O是△ABE的外心,故C不符合题意;
∵OA=OE=OC,∴O是△ACE的外心,故D不符合题意.
故选B.
17.A
【解析】根据题意,可知线段AB的线段垂直平分线为x=4,然后由C点的坐标可求得圆心的横坐标为x=4,然后设圆的半径为r,则根据勾股定理可求解.
【解答】设圆的半径为r,则根据勾股定理可知:
false,解得r=false,
因此圆心的纵坐标为false,
因此圆心的坐标为(4,false).
故选A
考点:1、线段垂直平分线,2、三角形的外接圆,3、勾股定理
18.C
【解析】根据等边三角形的判定和性质,直角三角形的判定和性质,三角形的外心等知识一一判断即可.
【解答】解:由作图可知:AB=BC=AC,
∴△ABC是等边三角形,
∴∠A=60°,(故A正确)
∵BA=BC=BD,
∴△ACD是直角三角形,(故B正确),点B是△ACD的外心.(故D正确);
∴tanA=false=false,
∴AC=false,
∴BC=false,(故C错误)
故选C.
【点评】本题考查作图-基本作图,等边三角形的判定和性质,直角三角形的判定和性质,三角形的外心等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
19.线段的垂直平分线的性质
【解析】利用线段垂直平分线的性质得到OA=OC=OB,然后根据点与圆的位置关系可判断点A、C在⊙O上.
【解答】解:如图,连接false,
∵点O为AC和BC的垂直平分线的交点,
∴OA=OC=OB,
∴⊙O为false的外接圆.
故答案为:线段的垂直平分线的性质.
【点评】本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.考查线段的垂直平分线的性质,确定圆的条件,掌握作图的原理是解题的关键.
20.在圆外
【解析】根据点到直线距离垂线段最短,AB>AD,即AB>r,所以点B与⊙A的位置关系在圆外.
【解答】解:∵AB=AC,作AD⊥BC,
∴AB>AD,即AB>r,
∴点B与⊙A的位置关系在圆外.
故答案为:在圆外
【点评】本题考查了点与圆的位置关系定理和勾股定理等知识点的应用,点与圆(圆的半径是r,点到圆心的距离是d)的位置关系有3种:d=r时,点在圆上;d<r点在圆内;d>r点在圆外.
21.A B M
【解析】先求出AB的长,根据直角三角形斜边上的中线等于斜边的一半,求得CM的长,再由点与圆的位置关系,确定出点A,B,M与⊙C的位置关系.
【解答】解:∵∠ACB=90°,AC=2cm,BC=4cm,∴AB=false=2false.
∵CM是中线,∴CM=falseAB=false,∴M在圆上.
∵AC=2<false,∴A在圆内.
∵BC=4>false,∴B在圆外.
故答案为A,B,M.
【点评】本题考查了点与圆的位置关系:①点P在⊙O上;②点P在⊙O内;③点P在⊙O外,及勾股定理的运用.
22.(2,2).
【解析】
【解析】连结OA,根据勾股定理可求OA,再根据点与圆的位置关系可得一个符合要求的点B的坐标.
【解答】如图,连结OA,
OA=false=5,
∵B为⊙O内一点,
∴符合要求的点B的坐标(2,2)答案不唯一.
故答案为:(2,2).
【点评】考查了点与圆的位置关系,坐标与图形性质,关键是根据勾股定理得到OA的长.
23.甲 内错角相等,两直线平行;一组对边平行且相等的四边形是平行四边形;平行四边形对角相等
【解析】甲:由内错角相等,两直线平行;一组对边平行且相等的四边形是平行四边形;平行四边形对角相等可得;
乙:由线段垂直平分线上的点到这条线段两个端点的距离相等;圆的确定;同弧所对的圆周角相等可得.
【解答】解:甲、∵∠CAD=∠ACB,
∴AD∥BC,
又∵AP=CB,
∴四边形ABCP是平行四边形,
∴∠B=∠APC,
故甲作法的依据为:内错角相等,两直线平行;一组对边平行且相等的四边形是平行四边形;平行四边形对角相等.
乙、∵a为AB的中垂线、b为BC的中垂线,且交点为O,
∴OA=OB=OC,
∴点A、B、C在以O为圆心、OA为半径的圆上,
∴∠APC=∠ABC,
故乙作法的依据是:线段垂直平分线上的点到这条线段两个端点的距离相等;圆的确定;同弧所对的圆周角相等.
故答案为:甲、内错角相等,两直线平行;一组对边平行且相等的四边形是平行四边形;平行四边形对角相等.
【点评】本题主要考查作图﹣复杂作图,熟练掌握平行四边形的判定及中垂线的性质、圆周角定理是解题的关键.
24.false外, ⊙O内, 5
【解析】
【解析】首先根据圆的面积求出圆的半径,然后由点与圆的位置关系即可求解.
【解答】因为圆的面积为25πcm2,所以圆的半径为5cm.
若OP=6.5cm,因为6.5cm>5cm,则点P在⊙O外;
若OP=4cm,因为4cm<5cm,则点P在⊙O内;
若OP=5cm,则点P在⊙O上.
故答案为⊙O外;⊙O内;5.
【点评】本题考查的是点与圆的位置关系,点与圆的位置关系有3种.设⊙O的半径为r,点P到圆心的距离OP=d,则有:①点P在圆外?d>r;②点P在圆上?d=r;③点P在圆内?d<r.
25.三角形内 斜边上 三角形外
【解析】
试题分析:三角形外接圆的圆心叫做三角形的外心.三角形外接圆的圆心也就是三角形三边垂直平分线的交点,所以锐角三角形的垂直平分线交点在三角形内,直角三角形的垂直平分线的交点在斜边上,钝角三角形的垂直平分线的交点在三角形外.
26.直角
【解析】三角形外接圆的圆心是三角形的外心,外心到三个顶点的距离相等,由此即可判断三角形的形状.
【解答】∵三角形外接圆的圆心是三角形的外心,
∴外心到三个顶点的距离相等,
∵外心在三角形的一边上,
∴外心到该边上两个端点的距离相等,
由此得到外心到三角形第三个顶点的距离等于此边的一半,
∴该三角形是直角三角形,
故答案为:直角.
【点评】此题考查三角形外心的定义,正确掌握定义并运用解题是关键.
27.(6,6)
【解析】如图:由题意可得M在AB、BC的垂直平分线上,则BN=CN;证得ON=OB+BN=6,即△OMN是等腰直角三角形,得出MN=ON=6,即可得出答案.
【解答】解:如图∵圆M是△ABC的外接圆
∴点M在AB、BC的垂直平分线上,
∴BN=CN,
∵点A,B,C的坐标分别是(0,4),(4,0),(8,0)
∴OA=OB=4,OC=8,
∴BC=4,
∴BN=2,
∴ON=OB+BN=6,
∵∠AOB=90°,
∴△AOB是等腰直角三角形,
∵OM⊥AB,
∴∠MON=45°,
∴△OMN是等腰直角三角形,
∴MN=ON=6,点M的坐标为(6,6).
故答案为(6,6).
【点评】本题考查了三角形的外接圆与外心、坐标与图形性质、等腰直角三角形的判定与性质等知识,其中判定△OMN为等腰直角三角形是解答本题的关键.
28.false.
【解析】先根据勾股定理求出AB的长,进而得出CD的长,由点与圆的位置关系即可得出结论.
【解答】解:∵Rt△ABC中,∠ACB=90,AC=3,BC=false,
∴AB=false=4.
∵CD⊥AB,
∴CD=false.
∵AD?BD=CD2,
设AD=x,BD=4-x.
解得x=false,
∴点A在圆外,点B在圆内,
r的范围是false,
故答案为false.
【点评】本题考查的是点与圆的位置关系,熟知点与圆的三种位置关系是解答此题的关键.
29.该尺规作图的依据为:四边相等的四边形是菱形、有一个角为 60°的等腰三角形是等边三角形、圆的定义.
【解析】
【解析】由作图知AB=OB=OC=AC可判定四边形ABOC为菱形,根据∠BAC=120°知∠BAO=∠CAO=60°,从而得∠BAO=∠CAO=60°,即△OAB、△OAC为等边三角形,继而由OB=OA=OC可得所求作的圆.
【解答】如图,连接OA、OC,
由作图知BA=BO、OC=OA,
∵AB=AC,
∴AB=OB=OC=AC,
∴四边形ABOC为菱形(四边形相等的四边形是菱形),
又∵∠BAC=120°,
∴∠BAO=∠CAO=60°,
则△OAB、△OAC为等边三角形(有一个角为60°的等腰三角形是等边三角形),
∴OB=OA=OC,
∴点A、B、C在以O为圆心、OB为半径的圆上(圆的定义),
综上,该尺规作图的依据为:四边形相等的四边形是菱形、有一个角为60°的等腰三角形是等边三角形、圆的定义.
【点评】本题主要考查作图-复杂作图,解题的关键是熟练掌握菱形的判定与性质、等边三角形的判定与性质及圆的定义.
30.false
【解析】根据三角形的外心是三边中垂线的交点,由B、C的坐标可知,圆心M必在直线x=1上;由图知:AC的垂直平分线正好经过(1,0),由此可得到M(1,0);连接MB,过M作MD⊥BC于D,由勾股定理即可求得 M的半径长.
【解答】设△ABC的外心为M;
∵B(?2,?2),C(4,?2),
∴M必在直线x=1上,
由图知:AC的垂直平分线过(1,0),
故M(1,0);
过M作MD⊥BC于D,连接MB,
Rt△MBD中,MD=2,BD=3,
由勾股定理得:MB=false=false,
即△ABC的外接圆半径为false.
故答案为false.
【点评】本题考查了三角形的外接圆与外心与坐标与图形性质,解题的关键是熟练的掌握三角形的外接圆与外心与坐标与图形性质.
31.false
【解析】设∠DCE=x,∠ACD=y,根据等腰三角形的性质求出∠ACE、∠BDC,根据三角形内角和定理求出∠DCE=45°,根据三角形的外接圆和外心的概念求出答案.
【解答】
设∠DCE=x,∠ACD=y,则∠ACE=x+y,∠BCE=90°?∠ACE=90°?x?y,
∵AE=AC,
∴∠ACE=∠AEC=x+y,
∵BD=BC,
∴∠BDC=∠BCD=∠BCE+∠DCE=90°?x?y+x=90°?y,
在△DCE中,∵∠DCE+∠CDE+∠DEC=180°,
∴x+(90°?y)+(x+y)=180°,
解得x=45°,
∴∠DCE=45°,
∵AC=6,BC=8,
∴AB=false =10,
∵AE=AC=6,BD=BC=8,
∴DE=4,又∠DCE=45°,
如图,作直径CH,连接HE,
∴∠CEH=90°,又∠CHE=∠DCE=45°,CE=4,
∴CH=4false,
即△DCE的外接圆的直径4false,
∴△DCE的外接圆的半径为2false.
【点评】本题考查了三角形的外接圆与外心相关知识点,解题的关键是熟练的掌握三角形的外接圆与外心的性质.
32.相交
【解析】首先求出方程的根,即可得到半径长度,再比较半径与false的大小关系即可判断直线AB与⊙O的位置关系.
【解答】解:∵⊙O的半径是一元二次方程x2+6x﹣16=0的解,
解方程x2+6x﹣16=0,
(x+8)(x﹣2)=0,
解得:x1=﹣8(舍去),x2=2,
∴r=2,
∵点O到直线AB距离d是false,
∴d<r,
∴直线AB与圆相交.
故答案为:相交.
【点评】本题考查解一元二次方程,点与圆的位置关系. 点O到直线AB的距离为d,若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.
33.6
如图,连接AC,∵?在矩形ABCD中,AB=8,AD=6,∠ABC=90°,
∴AC=false=false=false=10,
∴AD
∴点D一定在⊙A内,点C一定在⊙A外,
∴⊙A半径r的取值范围应大于AD的长,小于对角线AC的长,即6
【解析】首先利用直角三角形斜边上的中线等于斜边的一半的性质求出斜边AB的长,再利用直角三角形外心的位置特征得到斜边AB的长即为外接圆的直径,从而求出半径r.
【解答】解:在Rt△ABC中,∠ACB=90°,CD=5,D是AB的中点,
∴AB=2CD=10,
∵直角三角形的外心在斜边中点,
∴斜边AB即是△ABC外接圆的直径,
∴外接圆的半径r=5.
故答案为:5.
【点评】本题考查了直角三角形斜边中线等于斜边的一半的性质和直角三角形外心的位置特征,熟练掌握这些性质是解题的关键.
35.见解析.
【解析】根据垂径定理的推论可知:弦的垂直平分线过圆心,只需连接AC、BC,尺规作线段AC和BC的垂直平分线,其交点即为所求.
【解答】解:如图所示:
圆心O即为圆弧所在圆的圆心.
【点评】本题考查了尺规作线段的垂直平分线和垂径定理,属于基础题型,熟练掌握垂径定理和线段垂直平分线的尺规作图是关键.
36.(1)A1(0,﹣4),B1(3,﹣3),C1(3,﹣1);(2)(﹣2,﹣1)
【解析】(1)旋转以后易发现点A1,B1,C1的坐标;
(2)三角形外接圆的圆心为三角形各边垂直平分线的交点.
【解答】解:(1)△A1B1C1如图所示.A1(0,﹣4),B1(3,﹣3),C1(3,﹣1).
(2)△ABC的外接圆如图所示,
圆心O′的坐标为(﹣2,﹣1).
【点评】此题考查的是旋转和外接圆的圆心确定方法.
37.(1)false,false;(2)false
【解析】(1)先利用等面积法算出AF=false,再根据勾股定理得出false;
(2)根据题意点F只能在圆内,点C、D只能在圆外,所以⊙A的半径r的取值范围为false.
【解答】解:如图,
(1)在矩形false中,false,false.
∴DC=AB=3,AC=BD=false=5,
∵DE⊥AC,AF⊥BD,
∴false ;
∴AF=false,
同理,DE=false,
在Rt△ADE中,AE=false =false,
(2) 若以点false为圆心作圆, false、false、false、E、F五点中至少有1个点在圆内,则r>2.4,
当至少有2个点在圆外,r<4,
故⊙A的半径r的取值范围为:false
38.(1)130°,130°;(2)详见解析.
【解析】(1)由AB=AC,得到false=false,于是得到结论;
(2)连接OB,OC,由线段的垂直平分线的判定定理可得AD垂直平分BC,再由等腰三角形的三线合一性质可证得结论;
【解答】解:(1)∵AB=AC,
∴false=false,
∵false的度数=100°,
∴false和 false的度数=false=130°;
(2)证明:如图,连接OB,OC,延长AO交BC于D,
∵AB=AC,OB=OC,
∴点A和点O都在线段BC的垂直平分线上,
∴BD=CD,AD⊥BC,
∴∠BAD=∠CAD,
即AO平分∠BAC.
【点评】本题考查了三角形的外接圆与外心、线段垂直平分线的判定与性质、勾股定理等知识点,熟练掌握相关性质定理及其应用,是解题的关键.
39.点A在⊙O内,点B在⊙O上,点C在⊙O 外.
【解析】分别求出false、false、false三点到点false的距离,然后与圆的半径即可求得三点与圆的位置关系.
【解答】∵OA=== (cm)<r=10 cm,
OB===10(cm)=r,
OC=== (cm)>r=10 cm,
∴点A在⊙O内,点B在⊙O上,点C在⊙O 外.
【点评】本题考查了点与圆的位置关系,解题的关键是求得点与圆心的距离.
40.(1)见解析;(2)见解析
【解析】(1)结合圆内接四边形的性质和等腰三角形的性质,可知DE∥AB;
(2)结合圆周角定理及等腰三角形的性质和矩形的判定,可知四边形ADBF即为所求作.
【解答】(1)连接DE,DE即为所求;
(2)连接BD,AE相交于点M,连接CM并延长交AB于点O,连接DO并延长交圆于点N,连接AN,BN,四边形ADBN即为所求.
【点评】本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
41.(1)见解析;(2)见解析
【解析】根据内接三角形和等腰直角三角形的性质,结合题意即可得出答案.
【解答】解:(1)如图1,false即为所求(画法不唯一).
(2)如图2,false即为所求(画法不唯一)
【点评】本题主要考查了圆内接等腰直角三角形的作图方法,考查了学生的作图能力.
42.(1)见解析; (2) S△BOC75falsecm2.
【解析】(1)根据AI和BI分别是∠BAC和∠ABC的平分线来证明BD=CD,再证明∠ABI=∠CBI,∠DBC=∠BAD,求得∠DBI=∠DIB.即可;
(2)先求出∠BAD=∠CAD=∠BCD=60°.,证明△DBC是等边三角形,再求出BD即可.
【解答】(1)∵AI和BI分别是∠BAC和∠ABC的平分线,∴∠BAD=∠CAD,∠ABI=∠CBI.∴BD=CD,∠DBC=∠CAD=∠BAD.∵∠DBI=∠DBC+∠CBI.∠DIB=∠ABI+∠BAD.又∵∠ABI=∠CBI,∠DBC=∠BAD,∴∠DBI=∠DIB.∴BD=DI.∴DB=DC=DI (2)∵∠BAC=120°,∴∠BAD=∠CAD=∠BCD=60°.∵BD=DC,∴△DBC是等边三角形.∵⊙O的半径为10 cm,即BO=DO=CO=10 cm,∴BD=10false cm.∴S△BOC=false×(10false)2=75false (cm2)
【点评】本题考查的是三角形,熟练掌握熟练掌握三角形的外接圆是解题的关键.
43.(1)=;(2)△ACE是等腰直角三角形,理由见解析;(3)45°<α<90°
【解析】(1)利用四边形内角和等于360度得:∠B+∠ADC=180°,而∠ADC+∠EDC=180°,即可求解;
(2)证明△ABC≌△EDC(AAS)即可推知△ACE是等腰直角三角形;
(3)当∠ABC=α=90°时,△ABC的外心在其直角边上,∠ABC=α>90°时,△ABC的外心在其外部,即可求解.
【解答】解:(1)在四边形BADC中,∠B+∠ADC=360°﹣∠BAD﹣∠DCB=180°,
而∠ADC+∠EDC=180°,
∴∠ABC=∠PDC.
故答案是:=;
(2)△ACE是等腰直角三角形,理由如下:
∵∠ECD+∠DCA=90°,∠DCA+∠ACB=90°,
∴∠ACB=∠ECD.
由(1)知:∠ABC=∠PDC,
又∵BC=DC,
∴△ABC≌△EDC(AAS),
∴AC=CE.
又∵∠ACE=90°,
∴△ACE是等腰直角三角形;
(3)当∠ABC=α=90°时,△ABC的外心在其直角边上,
∠ABC=α>90°时,△ABC的外心在其外部,
而45°<α<135°,
故:45°<α<90°.
【点评】本题考查的是圆的综合运用,涉及到三角形全等、三角形外心等基本知识,难度不大.
44.(1)不是;(2)见解析;(3)∠C=78°或72°
【解析】(1)利用美好三角形的定义得出△ABC的形状进而求出即可;
(2)利用勾股定理的逆定理得出△ABC的形状进而得出答案;
(3)利用美好三角形的定义进而分别得出∠C的度数.
【解答】(1)解:∵△ABC中,∠A=40°,∠B=80°,
∴∠C=60°
∵402+602≠802,
∴△ABC不是美好三角形;
故答案为:不是;
(2)证明:连接OA、OC,
∵AC=2,OA=OC=false,
∴△OAC是直角三角形,即∠AOC=90°,
∴∠B=45°,
∵∠C=60°,
∴∠A=75°,
∵即三个内角满足关系:452+602=5625=752,
∴△ABC是美好三角形;
(3)解:设∠C=x°,则∠B=(150﹣x)°,
若∠C为最大角,则x2=(150﹣x)2+302,
解得x=78,
若∠B最大角,则(150﹣x)2=x2+302,
解得x=72,
综上可知,∠C=78°或72°
【点评】本题考查圆周角定理及其推论、三角形的外接圆与外心和解直角三角形,解题的关键是掌握圆周角定理及其推论、三角形的外接圆与外心和解直角三角形.
45.(1)见解析;(2)(2,0);(3)点D在⊙M内;
【解答】试题分析:(1)由网格容易得出AB的垂直平分线和BC的垂直平分线,它们的交点即为点M;
(2)根据图形即可得出点M的坐标;
(3)用两点间距离公式求出圆的半径和线段DM的长,当DM小于圆的半径时点D在圆内.
试题解析:解:(1)如图1,点M就是要找的圆心;
(2)圆心M的坐标为(2,0).故答案为(2,0);
(3)圆的半径AM=false=false.
线段MD=false=false<false,所以点D在⊙M内.
点睛:本题考查的是点与圆的位置关系,坐标与图形性质以及垂径定理,利用网格结构得到圆心M的坐标是解题的关键.
同课章节目录
