平行四边形判定学案(无答案)
文档属性
| 名称 | 平行四边形判定学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 177.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-31 00:00:00 | ||
图片预览

文档简介
19.1.2《平行四边形的判定》学案(1)
【学习目标】探索并掌握平行四边形的判定条件.
【学习重点】平行四边形的判定方法。
【学习难点】平行四边形的判定条件和方法的寻找。
【学习方法】自主-合作-探究
【学习过程】
一、复旧引新
1、回忆平行四边形的性质:
(1)从边看:平行四边形的两组对边分别 ;
平行四边形的两组对边分别 ;
(2)从角看:平行四边形的两组对角分别 ;
(3)从对角线看:平行四边形的两条对角线 .
2、类比平行线的性质与判定,将平行四边形性质中的条件和结论互换位置:
(1) (定义);
(2) ;
(3) ;
(4) .
二、探究新知
1.已知,在四边形ABCD中,AB=CD,AD=BC,求证:四边形ABCD是平行四边形。
﹡通过证明我发现: 的四边形是平行四边形。
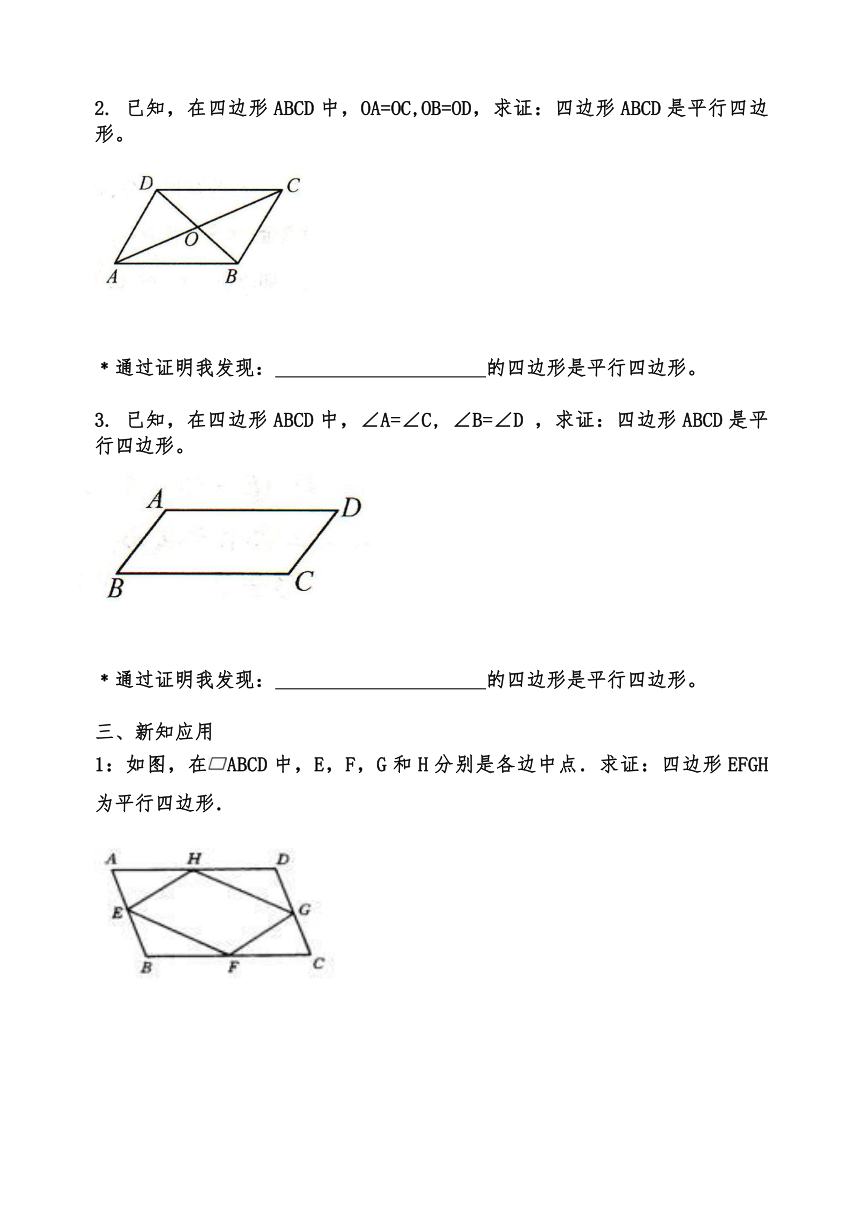
2. 已知,在四边形ABCD中,OA=OC,OB=OD,求证:四边形ABCD是平行四边形。
﹡通过证明我发现: 的四边形是平行四边形。
3. 已知,在四边形ABCD中,∠A=∠C, ∠B=∠D ,求证:四边形ABCD是平行四边形。
﹡通过证明我发现: 的四边形是平行四边形。
三、新知应用
1:如图,在ABCD中,E,F,G和H分别是各边中点.求证:四边形EFGH为平行四边形.
2、如图,ABCD的对角线AC,BD相交于点O,点E.F是AC上的两点,并且AE=CF。求证:四边形BFDE为平行四边形.
3、如图所示,已知□ABCD中,AE、CF分别是∠DAB、∠BCD的平分线,
求证:四边形AFCE是平行四边形。
四、当堂检测
1.如图,能够判定四边形ABCD是平行四边形的条件是( )
A.AB∥CD,AD=BC B. ∠A=∠B
C. AB=CD,AD=BC D. AB= AD ,CD =BC
2.如图,将平行四边形ABCD的对角线BD向两个方向延长,分别至点E和点F,且使BE=DF.求证,四边形AECF是平行四边形。
五、反思质疑
【学习目标】探索并掌握平行四边形的判定条件.
【学习重点】平行四边形的判定方法。
【学习难点】平行四边形的判定条件和方法的寻找。
【学习方法】自主-合作-探究
【学习过程】
一、复旧引新
1、回忆平行四边形的性质:
(1)从边看:平行四边形的两组对边分别 ;
平行四边形的两组对边分别 ;
(2)从角看:平行四边形的两组对角分别 ;
(3)从对角线看:平行四边形的两条对角线 .
2、类比平行线的性质与判定,将平行四边形性质中的条件和结论互换位置:
(1) (定义);
(2) ;
(3) ;
(4) .
二、探究新知
1.已知,在四边形ABCD中,AB=CD,AD=BC,求证:四边形ABCD是平行四边形。
﹡通过证明我发现: 的四边形是平行四边形。
2. 已知,在四边形ABCD中,OA=OC,OB=OD,求证:四边形ABCD是平行四边形。
﹡通过证明我发现: 的四边形是平行四边形。
3. 已知,在四边形ABCD中,∠A=∠C, ∠B=∠D ,求证:四边形ABCD是平行四边形。
﹡通过证明我发现: 的四边形是平行四边形。
三、新知应用
1:如图,在ABCD中,E,F,G和H分别是各边中点.求证:四边形EFGH为平行四边形.
2、如图,ABCD的对角线AC,BD相交于点O,点E.F是AC上的两点,并且AE=CF。求证:四边形BFDE为平行四边形.
3、如图所示,已知□ABCD中,AE、CF分别是∠DAB、∠BCD的平分线,
求证:四边形AFCE是平行四边形。
四、当堂检测
1.如图,能够判定四边形ABCD是平行四边形的条件是( )
A.AB∥CD,AD=BC B. ∠A=∠B
C. AB=CD,AD=BC D. AB= AD ,CD =BC
2.如图,将平行四边形ABCD的对角线BD向两个方向延长,分别至点E和点F,且使BE=DF.求证,四边形AECF是平行四边形。
五、反思质疑
