分式复习
图片预览








文档简介
(共26张PPT)
期中复习专题第八章:分式
灌南光明实验学校
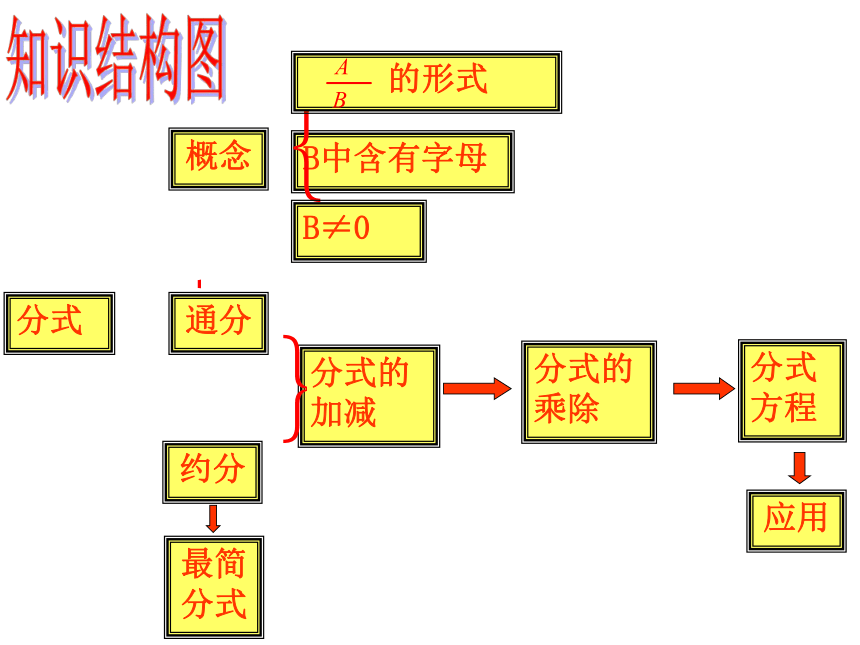
分式
概念
约分
通分
B中含有字母
分式的加减
分式的乘除
应用
的形式
B≠0
分式方程
最简分式
1.什么是分式
一般地,如果A、B表示两个整式,并且B中含
有字母,那么代数式 叫做分式.
在 、 、 、 、
中分式有哪些?
当x取何值时,下列分式有意义?何时值为0
1、当取什么值时,分式
(1)没有意义?(2)有意义?
(3)值为零。 (4) 值为负?
2、当x为何值时分式 的值为0
3、已知分式 当x≠______时,分式有意义;当x=______时,分式的值为0.
你会解决下面这些问题吗
2.分式的基本性质:
分式的分子和分母都乘以(或除以)同一个不等于0的整式,分式的值不变.
(其中M是不等于0的整式)
1.下列式子
(1) (2) ;
(3) ;(4)
中正确的是 ( )
A 、1个 B 、2 个 C、 3 个 D、 4 个
2.若将分式 (a、b均为正数)中的字母a、b的值分别扩大为原来的2倍,则分式的值为( )
A.扩大为原来的2倍 B.缩小为原来的
C.不变 D.缩小为原来的
4. 下列分式中,最简分式是 ( )
3.下列各式中不正确的变形是( )
(A) = (B) =
(C) = (D) =
3.什么是分式的约分?
根据分式的基本性质,把一个分式的分子和分母分别除以它们的公因式叫做分式的约分.
1: 约去分子和分母中相同字母(或含字母的式子)的
最低次幂,并约去系数的最大公约数即可.
2:分子、分母是多项式,要先将分子或分母分别
因式分解,找出它们的公因式,然后约分.
1.下列约分正确的是( )
A、 ; B、 ;
C、 ; D、
2.下列式子
(1) (2) ;
(3) ;(4)
中正确的是 ( )
A 、1个 B 、2 个 C、 3 个 D、 4 个
4.什么是最简分式?
一个分式的分子和分母没有公因式时叫做最简分式.约分通常要将分式化为最简分式或整式.
1.下列各分式中,最简分式是( )
A、
B、
D、
C、
2.计算:
5.
6.
分式的通分:
根据分式的基本性质,把几个异分母分式的分母化成相同,而分式的值不变,叫做分式的通分。
分式的加减:
同分母的分式相加减,分母不变,把分子相加减。
异分母的分式相加减,先通分,再加减。
1.分式
的最简公分母是 ;
的最简公分母是 .
2.通分
3.计算
4.化简并求值:
,其中
1
5.
解方程:
化简并求值:
应用:
1. 几位要好的同学准备结伴到某地游玩,预计共需
费用1200元,后来又有2名同学参加进来,但总
费用不变,于是每人可少分摊30元,试求原计划
结伴游玩的人数.
2.正在修建的高速公路上,有一段工程,若甲、乙两个工程队单独完成,甲工程队比乙工程队少用10天;若甲、乙两队合作,12天可以完成.求甲单独完成这项工程需要的天数.
我有哪些收获呢?
与大家共分享!
学 而 不 思 则 罔
回头一看,我想说…
期中复习专题第八章:分式
灌南光明实验学校
分式
概念
约分
通分
B中含有字母
分式的加减
分式的乘除
应用
的形式
B≠0
分式方程
最简分式
1.什么是分式
一般地,如果A、B表示两个整式,并且B中含
有字母,那么代数式 叫做分式.
在 、 、 、 、
中分式有哪些?
当x取何值时,下列分式有意义?何时值为0
1、当取什么值时,分式
(1)没有意义?(2)有意义?
(3)值为零。 (4) 值为负?
2、当x为何值时分式 的值为0
3、已知分式 当x≠______时,分式有意义;当x=______时,分式的值为0.
你会解决下面这些问题吗
2.分式的基本性质:
分式的分子和分母都乘以(或除以)同一个不等于0的整式,分式的值不变.
(其中M是不等于0的整式)
1.下列式子
(1) (2) ;
(3) ;(4)
中正确的是 ( )
A 、1个 B 、2 个 C、 3 个 D、 4 个
2.若将分式 (a、b均为正数)中的字母a、b的值分别扩大为原来的2倍,则分式的值为( )
A.扩大为原来的2倍 B.缩小为原来的
C.不变 D.缩小为原来的
4. 下列分式中,最简分式是 ( )
3.下列各式中不正确的变形是( )
(A) = (B) =
(C) = (D) =
3.什么是分式的约分?
根据分式的基本性质,把一个分式的分子和分母分别除以它们的公因式叫做分式的约分.
1: 约去分子和分母中相同字母(或含字母的式子)的
最低次幂,并约去系数的最大公约数即可.
2:分子、分母是多项式,要先将分子或分母分别
因式分解,找出它们的公因式,然后约分.
1.下列约分正确的是( )
A、 ; B、 ;
C、 ; D、
2.下列式子
(1) (2) ;
(3) ;(4)
中正确的是 ( )
A 、1个 B 、2 个 C、 3 个 D、 4 个
4.什么是最简分式?
一个分式的分子和分母没有公因式时叫做最简分式.约分通常要将分式化为最简分式或整式.
1.下列各分式中,最简分式是( )
A、
B、
D、
C、
2.计算:
5.
6.
分式的通分:
根据分式的基本性质,把几个异分母分式的分母化成相同,而分式的值不变,叫做分式的通分。
分式的加减:
同分母的分式相加减,分母不变,把分子相加减。
异分母的分式相加减,先通分,再加减。
1.分式
的最简公分母是 ;
的最简公分母是 .
2.通分
3.计算
4.化简并求值:
,其中
1
5.
解方程:
化简并求值:
应用:
1. 几位要好的同学准备结伴到某地游玩,预计共需
费用1200元,后来又有2名同学参加进来,但总
费用不变,于是每人可少分摊30元,试求原计划
结伴游玩的人数.
2.正在修建的高速公路上,有一段工程,若甲、乙两个工程队单独完成,甲工程队比乙工程队少用10天;若甲、乙两队合作,12天可以完成.求甲单独完成这项工程需要的天数.
我有哪些收获呢?
与大家共分享!
学 而 不 思 则 罔
回头一看,我想说…
