湘教版八年级下册数学 2.2.2用边判定平行四边形 教案
文档属性
| 名称 | 湘教版八年级下册数学 2.2.2用边判定平行四边形 教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 47.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-12 00:00:00 | ||
图片预览

文档简介
第
2
章
第
2
节
第
1
课时
授课
内容
用边判定平行四边形
授课
类型
习题讲授课
主备人
教学目标
知识与技能:理解平行四边形从边出发的三种判定方法,并学会简单应用。
过程与方法:在运用平行四边形的判定方法解决问题的过程中,通过有区别的标记条件、如何分析题目已知条件,获取解题思路,提高学生解决问题的能力。
情感态度与价值观:通过利用平行四边形从边出发的三种判定方法,使学生体会数学思想、
感受数学思考过程中的合理性,以及相互转化来分析问题。
重点难点
教学重点:平行四边形的判定定理(一,二,三)及应用.
教学难点:如何读题审题,确定解题思路,并书写出解题过程。
教学活动过程设计
教学环节
教
学
过
程
二次备课
随
感
一、复习
导入
最近学行四边形的判定,发现有些同学对于从边证
平行四边形掌握得不够好,这节课我们进行专项突破。
展示学习目标。
复习平行四边形的定义,性质,判定。
板书课题
展示知识框架
二、小试
身手
1、游戏大比拼;
利用判定定理选出合适的答案,
初步体会用边判
定平行四边形。
三、合作
探究
接下来利用相关知识解三个题,在题目中更深一层体会判
定。
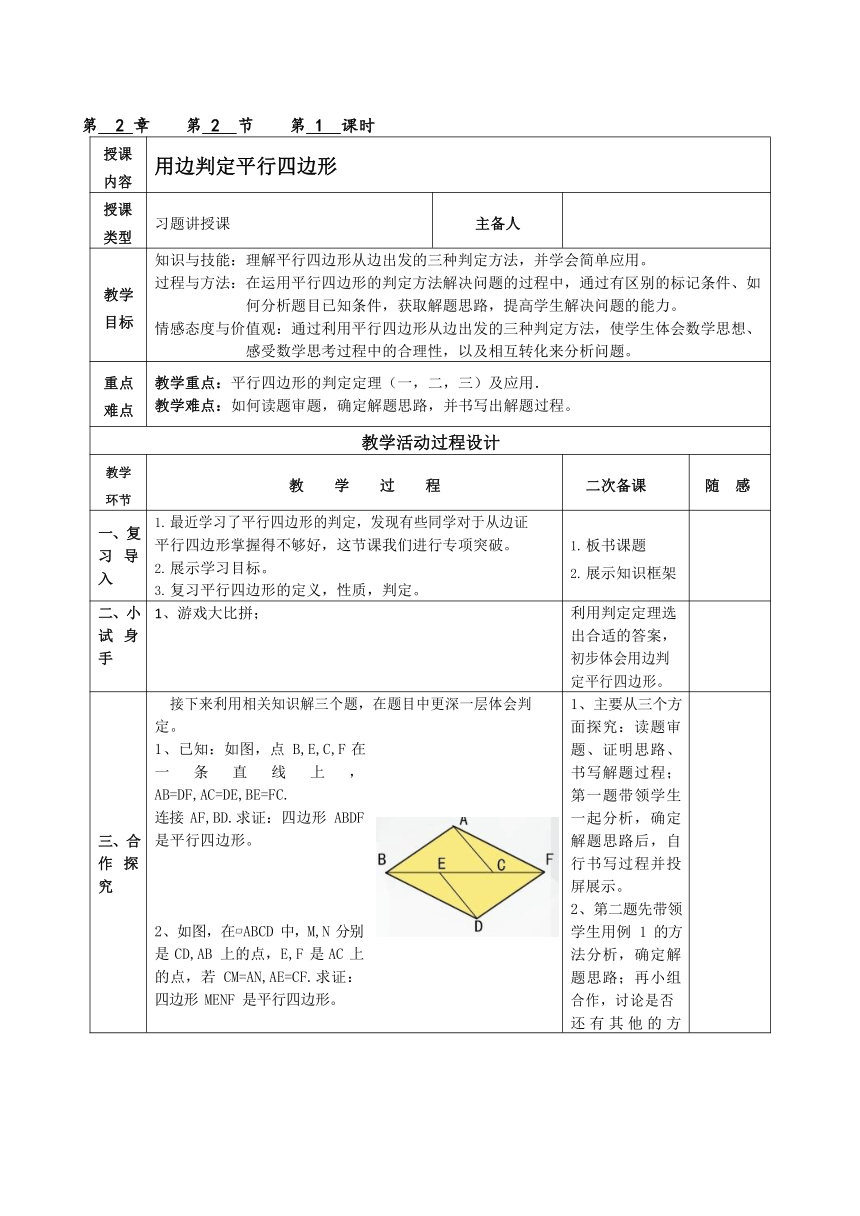
1、已知:如图,点
B,E,C,F
在一
条
直
线
上
,
AB=DF,AC=DE,BE=FC.
连接
AF,BD.求证:四边形
ABDF
是平行四边形。
2、如图,在?ABCD
中,M,N
分别是
CD,AB
上的点,E,F
是
AC
上的点,若
CM=AN,AE=CF.求证:
四边形
MENF
是平行四边形。
1、主要从三个方面探究:读题审题、证明思路、书写解题过程;
第一题带领学生一起分析,确定解题思路后,自行书写过程并投屏展示。
2、第二题先带领学生用例
1
的方法分析,确定解题思路;再小组合作,讨论是否
还
有
其
他
的
方
法,并请同学上台展示。
3.板书出三种方法的解题思路,
并分析哪一种方法最简洁,体会数
学
的
推
导
过程。
4
、体会数学思
想。
四、巩固
提升
3、如图,在四边形
ABCD
中,
BC⊥
CD,
各边的长在图中已标出。求证:四边形
ABCD
是平行四边形。
变式训练:培养学生观察图,确定合适的解题思路,体会数学数形结合、相互转
化的数学思想。
4、如图,在?ABCD
中,E,F,是对角线
AC
上的两点,
且
AE=CF.
求证:四边形
BFDE
是平行四边形。
学生上台说出解
五、课
题思路,查看掌
堂
小
握情况,培养学
测
生的表达能力和
自信。
六、课堂
小结
1、用边判定平行四边形的方法技巧,已知一组对边相等和一
组对边平行分别会有哪些思路。
2.几何证明的基本步骤。
梳
理
整
堂
课
内容,培养学生的学习能力,使学生思路更清晰,
突出重点、突破
难点。
教
学
反
思
2
章
第
2
节
第
1
课时
授课
内容
用边判定平行四边形
授课
类型
习题讲授课
主备人
教学目标
知识与技能:理解平行四边形从边出发的三种判定方法,并学会简单应用。
过程与方法:在运用平行四边形的判定方法解决问题的过程中,通过有区别的标记条件、如何分析题目已知条件,获取解题思路,提高学生解决问题的能力。
情感态度与价值观:通过利用平行四边形从边出发的三种判定方法,使学生体会数学思想、
感受数学思考过程中的合理性,以及相互转化来分析问题。
重点难点
教学重点:平行四边形的判定定理(一,二,三)及应用.
教学难点:如何读题审题,确定解题思路,并书写出解题过程。
教学活动过程设计
教学环节
教
学
过
程
二次备课
随
感
一、复习
导入
最近学行四边形的判定,发现有些同学对于从边证
平行四边形掌握得不够好,这节课我们进行专项突破。
展示学习目标。
复习平行四边形的定义,性质,判定。
板书课题
展示知识框架
二、小试
身手
1、游戏大比拼;
利用判定定理选出合适的答案,
初步体会用边判
定平行四边形。
三、合作
探究
接下来利用相关知识解三个题,在题目中更深一层体会判
定。
1、已知:如图,点
B,E,C,F
在一
条
直
线
上
,
AB=DF,AC=DE,BE=FC.
连接
AF,BD.求证:四边形
ABDF
是平行四边形。
2、如图,在?ABCD
中,M,N
分别是
CD,AB
上的点,E,F
是
AC
上的点,若
CM=AN,AE=CF.求证:
四边形
MENF
是平行四边形。
1、主要从三个方面探究:读题审题、证明思路、书写解题过程;
第一题带领学生一起分析,确定解题思路后,自行书写过程并投屏展示。
2、第二题先带领学生用例
1
的方法分析,确定解题思路;再小组合作,讨论是否
还
有
其
他
的
方
法,并请同学上台展示。
3.板书出三种方法的解题思路,
并分析哪一种方法最简洁,体会数
学
的
推
导
过程。
4
、体会数学思
想。
四、巩固
提升
3、如图,在四边形
ABCD
中,
BC⊥
CD,
各边的长在图中已标出。求证:四边形
ABCD
是平行四边形。
变式训练:培养学生观察图,确定合适的解题思路,体会数学数形结合、相互转
化的数学思想。
4、如图,在?ABCD
中,E,F,是对角线
AC
上的两点,
且
AE=CF.
求证:四边形
BFDE
是平行四边形。
学生上台说出解
五、课
题思路,查看掌
堂
小
握情况,培养学
测
生的表达能力和
自信。
六、课堂
小结
1、用边判定平行四边形的方法技巧,已知一组对边相等和一
组对边平行分别会有哪些思路。
2.几何证明的基本步骤。
梳
理
整
堂
课
内容,培养学生的学习能力,使学生思路更清晰,
突出重点、突破
难点。
教
学
反
思
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
