黑龙江省鹤岗市绥滨县2020-2021学年八年级下学期期末考试数学试题(word版含答案)
文档属性
| 名称 | 黑龙江省鹤岗市绥滨县2020-2021学年八年级下学期期末考试数学试题(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 305.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 23:16:04 | ||
图片预览



文档简介
(
)绥滨县中小学2020——2021学年度下学期期末考试
八年级数学试题
学
校
班
级
姓
名
考
号
考生注意:
考试时间120分钟
全卷共三道大题,总分120分
题号
一
二
三
总分
21
22
23
24
25
26
27
28
得分
得分
评卷人
选择题:(每小题3分,共30分)
1.下列式子中,属于最简二次根式的是(
)
A.
B.
C.
D.
2.
下列四边形中,是中心对称图形,但不是轴对称图形的是(
)
A.平行四边形
B.矩形
C.菱形
D.正方形
3.如图,在中,平分,则的长是(
)
A.2
B.3
C.4
D.5
4.下列计算正确的是( )
A.
B.
=-2
C.=x
D.
5.直角三角形三边的长分别为3、4、x,则x可能取的值为(??
)
A.5
B.
C.5或
D.不能确定
6.甲、乙、丙、丁四人各进行了10次射击测试,他们的平均成绩相同,方差分别是,则射击成绩最稳定的是(
)
A.甲
B.乙
C.丙
D.丁
7.函数y=(2-a)x+b-1是正比例函数的条件是(?
?)
A.a≠2??B.b=1
?C.a≠2且b=1????D.a,b可取任意实数
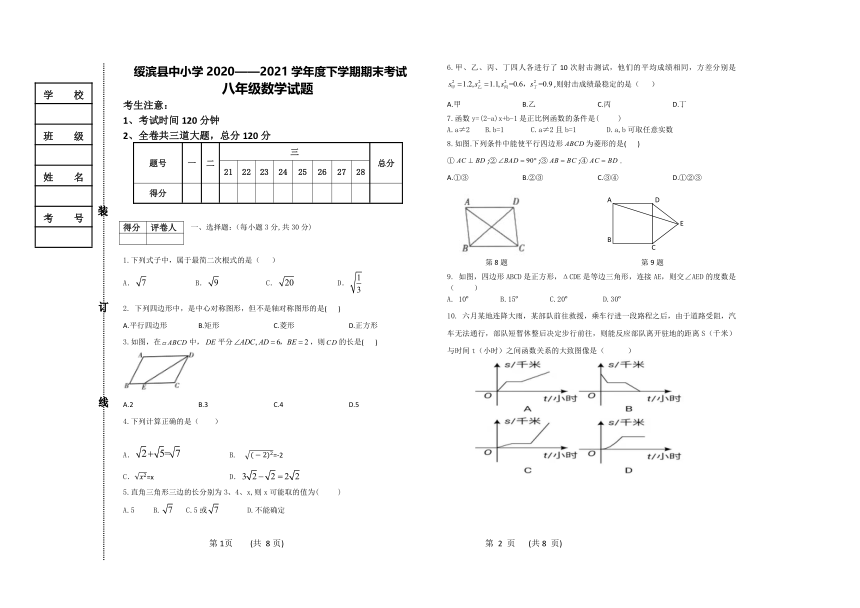
8.如图.下列条件中能使平行四边形为菱形的是(
)
①;②;③;④.
A.①③
B.②③
C.③④
D.①②③
(
A
B
C
D
E
)
第8题
第9题
如图,四边形ABCD是正方形,ΔCDE是等边三角形,连接AE,则交∠AED的度数是
(
)
10?
B.15?
C.20?
D.30?
六月某地连降大雨,某部队前往救援,乘车行进一段路程之后,由于道路受阻,汽车无法通行,部队短暂休整后决定步行前往,则能反应部队离开驻地的距离S(千米)与时间t(小时)之间函数关系的大致图像是(
)
得分
评卷人
填空题:(每小题3分,共30分)
11.函数Y=
中自变量x的取值范围是________
12.已知△ABC中,AB=k,AC=k-1,BC=3,当k=_________时,∠C=90°
13.已知函数y=(3k+6)x-k,函数值y随x的增大而减小,则k的取值范围是??????????????
14.如图,沿江公园有一块长方形草坪,少数游人会图方便走“捷径”,在草坪内走出了一条“路”,他们仅仅少走了__________m路,却踩伤了花草.
15.如果P(2,m),A(1,1),B(4,0)三点在同一直线上,则m的值为________
16.直线与直线相交于点,则方程组,的解是__________.
17.平行四边形ABCD的一个内角的平分线把一条边分成4cm和5cm两段,则平行四边形ABCD的周长为__________
如图,O是坐标原点,菱形OABC的顶点A的坐标为
(3,4),顶点C在x轴的正半轴上,则∠AOC的角平分线所在
直线的函数关系式为__________.
19.
如图,将菱形纸片折叠,使点A恰好落在菱形的对称中心O处,折痕为,若菱形的边长为,,则__________cm.
第19题
第20题
20.如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方ACEF再
以对角线AE为边作第三个正方形
AEGH,如此下去,则第n个正方形的边长为________
得分
评卷人
三、解答题(满分60分)
21.计算(本题满分6分)
计算:(1)
(2)
得分
评卷人
22.(每小题3分,共6分)
先化简,再求值
,其中
(
D
G
E
A
B
C
F
H
)
得分
评卷人
23.(本题满分6分)
一次函数图像经过(-2,1)和(1,3)两点。(1)求这个一次函数的解析式
(2)当x=3时,求y的值
得分
评卷人
学
校
班
级
姓
名
考
号
24.(本题满分8分)
近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”
方式之一,自2016年国庆后,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数
0
1
2
3
4
5
人数
11
15
23
28
18
5
(1)这天部分出行学生使用共享单车次数的中位数是____________,众数是____________
该中位数的意义是____________;
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3
次)的学生有多少人?
得分
评卷人
(本题满分8分)甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑摩托车,甲到达B地停留半小时后返回A地。如图是他们离A地的距离y(千米)与时间(时)之间的函数关系图像。(1)求甲从B地返回A的过程中,直接写出y与x之间的函数关系式及自变量x的取值范围。
(2)若乙出发后108分钟和甲相遇,求乙从A地到B地用了多少分钟。
(
(千米)
y
90
O
(时)
1
1.5
3
)
(
x
)
得分
评卷人
26.(本题满分6分)
如图,在△ABC中,∠CAB=90°,DE、DF
是△ABC的
中位线,连接EF,AD。求证:EF=AD
得分
评卷人
27.(本题满分10分)
某校举办数学竞赛,计划购买甲,乙两种奖品共30件。其中甲种奖品每件30元,乙种奖品每件20元。
(1)如果购买甲,乙两种奖品共花费800元,那么这两种奖品分别购买了多少件?
(2)若购买乙种奖品的件数不超过甲种奖品件数的3倍。如何购买甲、乙两种奖品,使得总花费最少?
得分
评卷人
(本题满分10分)
如图(1),正方形ABCD的对角线AC,BD相交于点O,E是AC上一点,连接EB.过点A作AM⊥BE,垂足为M,AM与BD相交于F。
求证:OE=OF
如图2,若点E在AC的延长线上,AM⊥BE于点M,AM交DB的延长线于点F,其他条件不变,结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由。
绥滨县2020——2021学年下学期期末考试
八年级数学试题答案
一、选择题(每小题3分,共30分)
1.A
2.A
3.C
4.D
5.C
6.C
7.C
8.A
9.B
10.A
二、填空题(每题3分)(第8题酌情给分)
11.x≥-2
2.5
13.k<-2
14.
2
15.
16.
17.26cm或28cm
18.y=
x
19.
20.
三、解答题(共60分)(解答题如有不同解法,可酌情给分)
21.计算(本题满分6分)
解:
(1)
-3+
(2)原式=-1+2-1
=4-+.....2分
=3-1+2-1
.......2分
=
.......3
分
=1+2.......3分
22.(本题满分6分)
解:
...........2分
...........
4分
........6分
(本题满分6分)
解:设一次函数为y=kx+b(k≠0)
.......1分
将(-2,1)和(1,3)代入,得
.......2分
解得
.......3分
∴一次函数为y=x+
.......4分
(2)一次函数为y=x+
当x=3时,y=
.......6分
24.(本题满分8分)
解:(1)3;3;—半人使用共享单车的次数在3次以上(含3次).
∵将数据从小到大排列后,排名次数在第50、51的都是3,∴中位数是3;∵3出现了28次,出现次数最多,∴众数是3;中位数表示一半人使用共享单车的次数在3次以上(含3次).
.......3分
(次)
答:这天部分出行学生平均每人使用共享单车约2次.
.......6分
(3)(人)
答:估计这天使用共享单车次数在3次以上(含3次)的学生
有765人
.......8分
25.(本题满分8分)
解:(1)设函数关系是为y=kx+b(k≠0).......1分
∵函数过点(1.5,90)和(3,0)
∴
.......3分
解得
.......4分
∴函数关系式为y=-60x
+180
X的取值范围为1.5≤x≤3
.......5分
(2)当x==1.8时
y=-60×1.8+180=72
.......6分
所以骑摩托车的速度为72÷1.8=40(千米/时)
.......7分
所以从乙从A地到B地用了90÷40=2.25(小时)=135分钟
.......8分
(本题满分6分)
证明:∵DE、DF是△ABC的中位线
∴DE//AB,
DF//AC
∴四边形AEDF是平行四边形
.......2分
∵∠BAC=90°
∴平行四边形AEDF是矩形
.......4分
∴EF=AD
.......6分
(本题满分10分)
解:(1)设购买了甲种奖品x件,购买了乙种奖品y件,则有
.......3分
解方程组,得
答:购买了甲种奖品20件,购买了乙种奖品10件
.......5分
设甲种奖品购买了t件,则乙种奖品购买了(30-t)件,设购买两种奖品的总费用为w元,
购买乙种奖品的件数不超过甲种奖品的3倍,则有
t≤3t
解得t≥7.5
.......7分
购买两种奖品的总费用:
w=30t+20(30-t)=10t+600
∵10>0
∴w随t的增大而增大
.......9分
∵t≥7.5且t为整数
∴当t=8时,w有最小值为w=10×8+600=680
答:当购买甲种奖品8件,乙种奖品22件,总花费最小,最小费用为680元
.......10分
(本题满分10分)
证明:(1)∵四边形ABCD是正方形
∴∠BOE=∠AOF=90?
OB=OA
........1分
∵AM⊥BE
∴∠MEA+∠MAE=90?=∠AFO+∠MAE
∴∠MEA=∠AFO
.........2分
在ΔBOE和ΔAOF中
∵
∠BOE=∠AOF
BO=AO
∠BEO=∠AFO
∴
ΔBOE≌ΔAOF
.......
4分
∴
OE=OF
.......5分
OE=OF成立
.......6分
∵四边形ABCD是正方形
∴∠BOE=∠AOF=90?
OB=OA
.......7分
∵AM⊥BE
∴∠F+∠MBF=90°∠E+∠OBE=90°
∵∠MBF=∠OBE
∴∠F=∠E
.......8分
在ΔBOE和ΔAOF中
∵
∠BOE=∠AOF
BO=AO
∠F=∠E
∴
ΔBOE≌ΔAOF
∴
OE=OF
.......10分
第1页 (共
8页)
第
2
页
(共8
页)
)绥滨县中小学2020——2021学年度下学期期末考试
八年级数学试题
学
校
班
级
姓
名
考
号
考生注意:
考试时间120分钟
全卷共三道大题,总分120分
题号
一
二
三
总分
21
22
23
24
25
26
27
28
得分
得分
评卷人
选择题:(每小题3分,共30分)
1.下列式子中,属于最简二次根式的是(
)
A.
B.
C.
D.
2.
下列四边形中,是中心对称图形,但不是轴对称图形的是(
)
A.平行四边形
B.矩形
C.菱形
D.正方形
3.如图,在中,平分,则的长是(
)
A.2
B.3
C.4
D.5
4.下列计算正确的是( )
A.
B.
=-2
C.=x
D.
5.直角三角形三边的长分别为3、4、x,则x可能取的值为(??
)
A.5
B.
C.5或
D.不能确定
6.甲、乙、丙、丁四人各进行了10次射击测试,他们的平均成绩相同,方差分别是,则射击成绩最稳定的是(
)
A.甲
B.乙
C.丙
D.丁
7.函数y=(2-a)x+b-1是正比例函数的条件是(?
?)
A.a≠2??B.b=1
?C.a≠2且b=1????D.a,b可取任意实数
8.如图.下列条件中能使平行四边形为菱形的是(
)
①;②;③;④.
A.①③
B.②③
C.③④
D.①②③
(
A
B
C
D
E
)
第8题
第9题
如图,四边形ABCD是正方形,ΔCDE是等边三角形,连接AE,则交∠AED的度数是
(
)
10?
B.15?
C.20?
D.30?
六月某地连降大雨,某部队前往救援,乘车行进一段路程之后,由于道路受阻,汽车无法通行,部队短暂休整后决定步行前往,则能反应部队离开驻地的距离S(千米)与时间t(小时)之间函数关系的大致图像是(
)
得分
评卷人
填空题:(每小题3分,共30分)
11.函数Y=
中自变量x的取值范围是________
12.已知△ABC中,AB=k,AC=k-1,BC=3,当k=_________时,∠C=90°
13.已知函数y=(3k+6)x-k,函数值y随x的增大而减小,则k的取值范围是??????????????
14.如图,沿江公园有一块长方形草坪,少数游人会图方便走“捷径”,在草坪内走出了一条“路”,他们仅仅少走了__________m路,却踩伤了花草.
15.如果P(2,m),A(1,1),B(4,0)三点在同一直线上,则m的值为________
16.直线与直线相交于点,则方程组,的解是__________.
17.平行四边形ABCD的一个内角的平分线把一条边分成4cm和5cm两段,则平行四边形ABCD的周长为__________
如图,O是坐标原点,菱形OABC的顶点A的坐标为
(3,4),顶点C在x轴的正半轴上,则∠AOC的角平分线所在
直线的函数关系式为__________.
19.
如图,将菱形纸片折叠,使点A恰好落在菱形的对称中心O处,折痕为,若菱形的边长为,,则__________cm.
第19题
第20题
20.如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方ACEF再
以对角线AE为边作第三个正方形
AEGH,如此下去,则第n个正方形的边长为________
得分
评卷人
三、解答题(满分60分)
21.计算(本题满分6分)
计算:(1)
(2)
得分
评卷人
22.(每小题3分,共6分)
先化简,再求值
,其中
(
D
G
E
A
B
C
F
H
)
得分
评卷人
23.(本题满分6分)
一次函数图像经过(-2,1)和(1,3)两点。(1)求这个一次函数的解析式
(2)当x=3时,求y的值
得分
评卷人
学
校
班
级
姓
名
考
号
24.(本题满分8分)
近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”
方式之一,自2016年国庆后,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数
0
1
2
3
4
5
人数
11
15
23
28
18
5
(1)这天部分出行学生使用共享单车次数的中位数是____________,众数是____________
该中位数的意义是____________;
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3
次)的学生有多少人?
得分
评卷人
(本题满分8分)甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑摩托车,甲到达B地停留半小时后返回A地。如图是他们离A地的距离y(千米)与时间(时)之间的函数关系图像。(1)求甲从B地返回A的过程中,直接写出y与x之间的函数关系式及自变量x的取值范围。
(2)若乙出发后108分钟和甲相遇,求乙从A地到B地用了多少分钟。
(
(千米)
y
90
O
(时)
1
1.5
3
)
(
x
)
得分
评卷人
26.(本题满分6分)
如图,在△ABC中,∠CAB=90°,DE、DF
是△ABC的
中位线,连接EF,AD。求证:EF=AD
得分
评卷人
27.(本题满分10分)
某校举办数学竞赛,计划购买甲,乙两种奖品共30件。其中甲种奖品每件30元,乙种奖品每件20元。
(1)如果购买甲,乙两种奖品共花费800元,那么这两种奖品分别购买了多少件?
(2)若购买乙种奖品的件数不超过甲种奖品件数的3倍。如何购买甲、乙两种奖品,使得总花费最少?
得分
评卷人
(本题满分10分)
如图(1),正方形ABCD的对角线AC,BD相交于点O,E是AC上一点,连接EB.过点A作AM⊥BE,垂足为M,AM与BD相交于F。
求证:OE=OF
如图2,若点E在AC的延长线上,AM⊥BE于点M,AM交DB的延长线于点F,其他条件不变,结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由。
绥滨县2020——2021学年下学期期末考试
八年级数学试题答案
一、选择题(每小题3分,共30分)
1.A
2.A
3.C
4.D
5.C
6.C
7.C
8.A
9.B
10.A
二、填空题(每题3分)(第8题酌情给分)
11.x≥-2
2.5
13.k<-2
14.
2
15.
16.
17.26cm或28cm
18.y=
x
19.
20.
三、解答题(共60分)(解答题如有不同解法,可酌情给分)
21.计算(本题满分6分)
解:
(1)
-3+
(2)原式=-1+2-1
=4-+.....2分
=3-1+2-1
.......2分
=
.......3
分
=1+2.......3分
22.(本题满分6分)
解:
...........2分
...........
4分
........6分
(本题满分6分)
解:设一次函数为y=kx+b(k≠0)
.......1分
将(-2,1)和(1,3)代入,得
.......2分
解得
.......3分
∴一次函数为y=x+
.......4分
(2)一次函数为y=x+
当x=3时,y=
.......6分
24.(本题满分8分)
解:(1)3;3;—半人使用共享单车的次数在3次以上(含3次).
∵将数据从小到大排列后,排名次数在第50、51的都是3,∴中位数是3;∵3出现了28次,出现次数最多,∴众数是3;中位数表示一半人使用共享单车的次数在3次以上(含3次).
.......3分
(次)
答:这天部分出行学生平均每人使用共享单车约2次.
.......6分
(3)(人)
答:估计这天使用共享单车次数在3次以上(含3次)的学生
有765人
.......8分
25.(本题满分8分)
解:(1)设函数关系是为y=kx+b(k≠0).......1分
∵函数过点(1.5,90)和(3,0)
∴
.......3分
解得
.......4分
∴函数关系式为y=-60x
+180
X的取值范围为1.5≤x≤3
.......5分
(2)当x==1.8时
y=-60×1.8+180=72
.......6分
所以骑摩托车的速度为72÷1.8=40(千米/时)
.......7分
所以从乙从A地到B地用了90÷40=2.25(小时)=135分钟
.......8分
(本题满分6分)
证明:∵DE、DF是△ABC的中位线
∴DE//AB,
DF//AC
∴四边形AEDF是平行四边形
.......2分
∵∠BAC=90°
∴平行四边形AEDF是矩形
.......4分
∴EF=AD
.......6分
(本题满分10分)
解:(1)设购买了甲种奖品x件,购买了乙种奖品y件,则有
.......3分
解方程组,得
答:购买了甲种奖品20件,购买了乙种奖品10件
.......5分
设甲种奖品购买了t件,则乙种奖品购买了(30-t)件,设购买两种奖品的总费用为w元,
购买乙种奖品的件数不超过甲种奖品的3倍,则有
t≤3t
解得t≥7.5
.......7分
购买两种奖品的总费用:
w=30t+20(30-t)=10t+600
∵10>0
∴w随t的增大而增大
.......9分
∵t≥7.5且t为整数
∴当t=8时,w有最小值为w=10×8+600=680
答:当购买甲种奖品8件,乙种奖品22件,总花费最小,最小费用为680元
.......10分
(本题满分10分)
证明:(1)∵四边形ABCD是正方形
∴∠BOE=∠AOF=90?
OB=OA
........1分
∵AM⊥BE
∴∠MEA+∠MAE=90?=∠AFO+∠MAE
∴∠MEA=∠AFO
.........2分
在ΔBOE和ΔAOF中
∵
∠BOE=∠AOF
BO=AO
∠BEO=∠AFO
∴
ΔBOE≌ΔAOF
.......
4分
∴
OE=OF
.......5分
OE=OF成立
.......6分
∵四边形ABCD是正方形
∴∠BOE=∠AOF=90?
OB=OA
.......7分
∵AM⊥BE
∴∠F+∠MBF=90°∠E+∠OBE=90°
∵∠MBF=∠OBE
∴∠F=∠E
.......8分
在ΔBOE和ΔAOF中
∵
∠BOE=∠AOF
BO=AO
∠F=∠E
∴
ΔBOE≌ΔAOF
∴
OE=OF
.......10分
第1页 (共
8页)
第
2
页
(共8
页)
同课章节目录
