2021-2022学年湘教版数学九年级上册3.4.2 相似三角形的性质课件(37张)
文档属性
| 名称 | 2021-2022学年湘教版数学九年级上册3.4.2 相似三角形的性质课件(37张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-12 00:00:00 | ||
图片预览







文档简介
(共37张PPT)
湘教版· 数学· 九年级(上)
3.4.2 相似三角形的性质
第三章 图形的相似
理解掌握相似三角形对应线段(高、中线、角平分线)及相似三角形的面积、周长比与相似比之间的关系。
学习目标
相似三角形的———————, 各对应边——————.
对应角相等
成比例
1.三角形相似的判定方法有那些?
两个角对应相等的两个三角形相似.
两边对应成比例且夹角相等的两个三角形相似 .
三边对应成比例的两个三角形相似.
2. 相似三角形的有哪些性质?
3.相似三角形还有哪些性质?
复习导入
思考
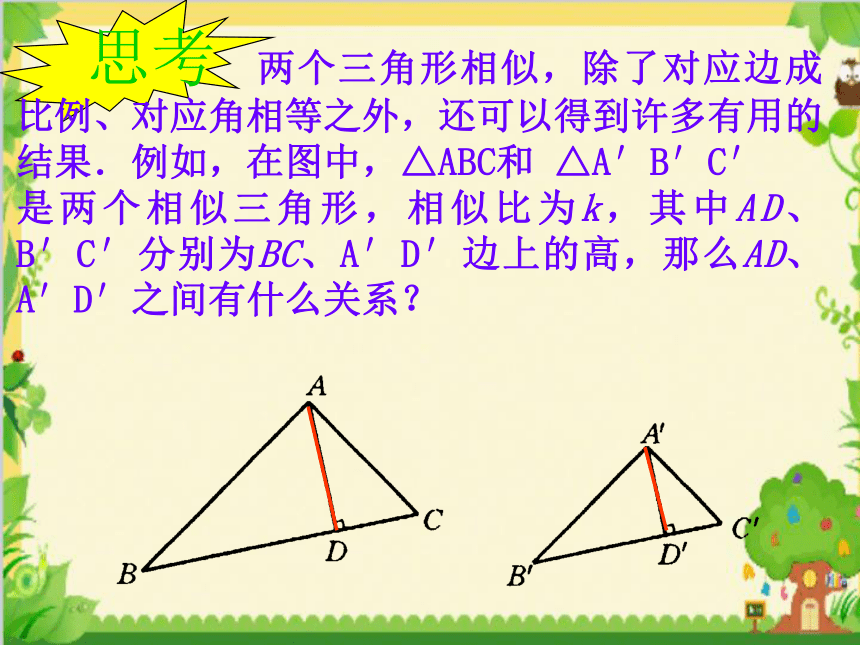
两个三角形相似,除了对应边成比例、对应角相等之外,还可以得到许多有用的结果.例如,在图中,△ABC和 △A′B′C′ 是两个相似三角形,相似比为k,其中AD、B′C′分别为BC、A′D′边上的高,那么AD、 A′D′之间有什么关系?
两角对应相等,两三角形相似
∽
∽
已知
所以∠B=∠B′( )
相似三角形的对应角相等
∽
( )
相似三角形的性质
结论:相似三角形对应高的比等于相似比
合作探究
问题2:如图, △ABC∽△ A′B′C′,相似比为K, AD 、 A′D′分别是BC 、 B′C′边上的中线.问:AD 、 A′D′之间有什么关系?
D'
C'
B'
A'
D
C
B
A
因为△ABC∽△ A′B′C′
所以
又
又 ∠B=∠B′
所以 △ABD∽△ A′B′D′
所以
结论:相似三角形对应中线的比等于相似比
解
所以
A′
C′
B′
C
B
A
E′
E
∽
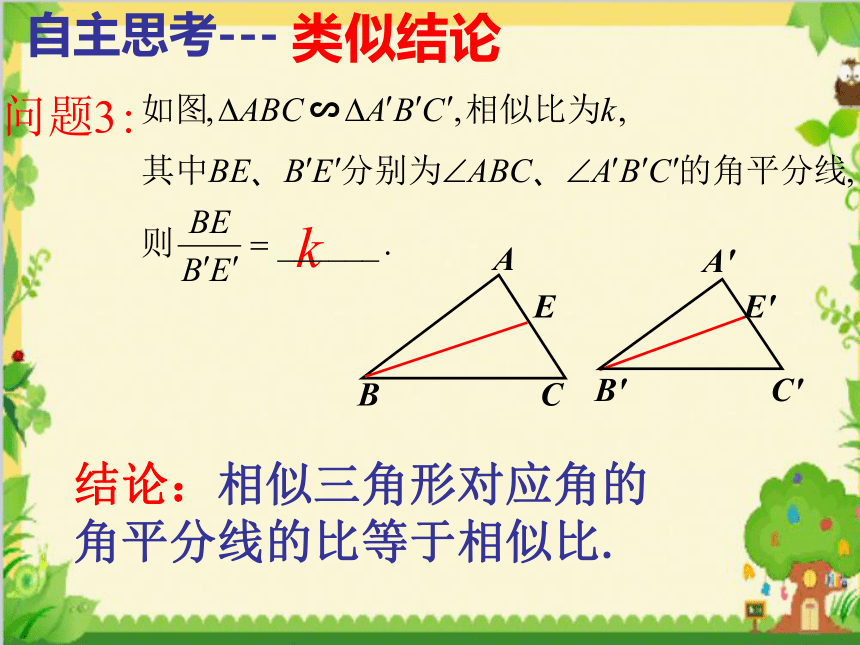
类似结论
自主思考---
结论:相似三角形对应角的角平分线的比等于相似比.
问题:4
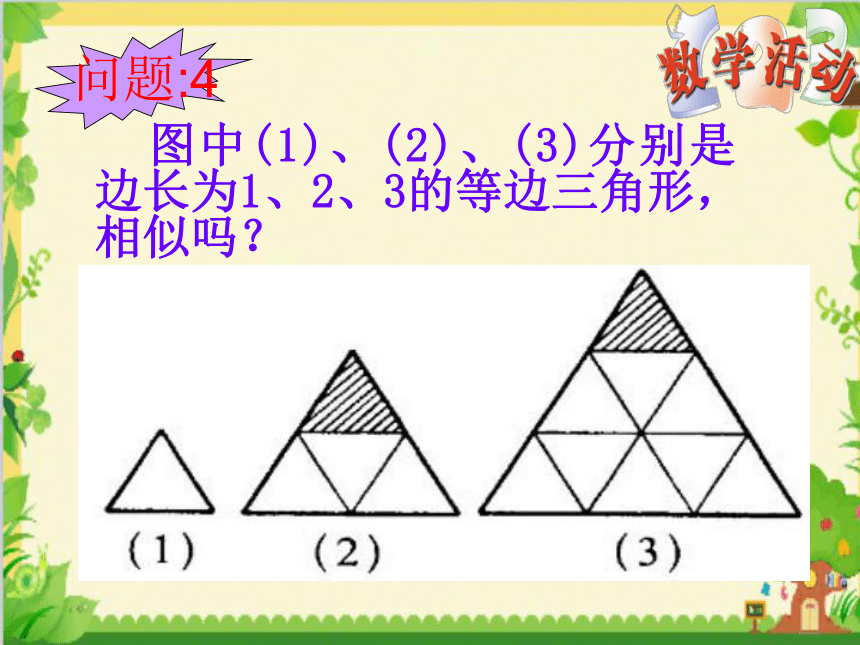
图中(1)、(2)、(3)分别是边长为1、2、3的等边三角形,相似吗?
(2)与(1)的相似比=____,
(2)与(1)的面积比=____;周长比=
(3)与(1)的相似比=_ __,
(3)与(1)的面积比= ___;周长比=
A
B
C
A’
B’
C’
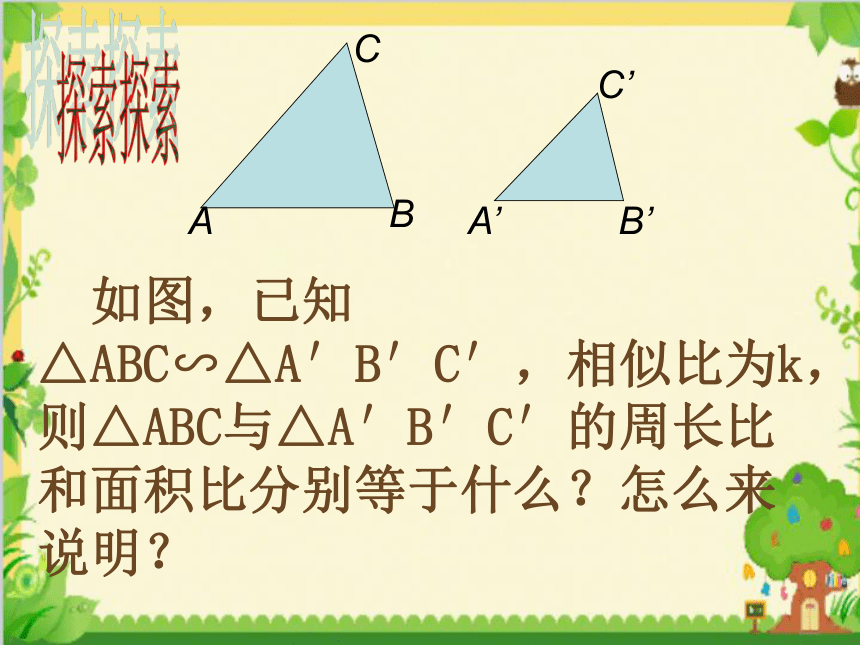
如图,已知△ABC∽△A′B′C′,相似比为k,则△ABC与△A′B′C′的周长比和面积比分别等于什么?怎么来说明?
A
B
C
A'
B'
C'
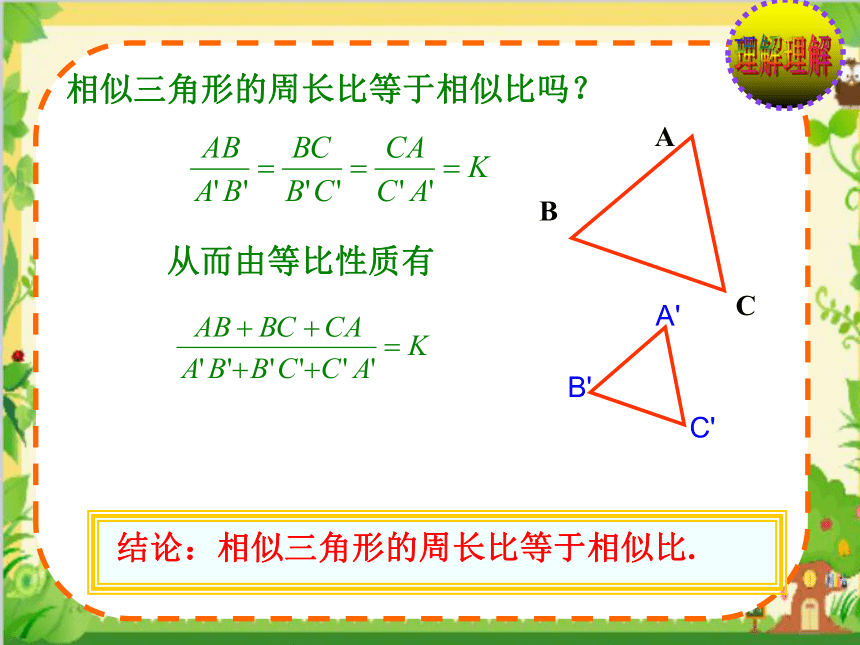
相似三角形的周长比等于相似比吗?
从而由等比性质有
结论:相似三角形的周长比等于相似比.
已知:如图, △ABC∽△A’B’C’,它们的相似比是K,
AD、A’D’分别是高.
求证:
证明: ∵△ABC∽△A’B’C’
B’
D’
C’
A’
A
B
C
D
结论:相似三角形的面积比等于相似比的平方.
通过前面的思考、探索、推理,我们得到相似三角形有如下性质;
相似三角形对应高的比、对应中线的比、对应角平分线的比、周长的比等于相似比.
相似三角形面积的比等于相似比的平方.
归纳总结:
已知△ABC∽△A′B′C′,相似比为2:3.
(1)如果AD,A′D′分别为这两个三角形的对应高,且AD=9cm,求A′D′的长.
(2)如果AE,A′E′分别为这两个三角形的对应中线,且A′E′=9cm,求AE的长.
(3)如果AF,A′F′分别为这两个三角形的对应角平分线,求 的值.
例: 如图,△ABC~△A'B'C',它们的周长分别是60厘米和72厘米,且AB=15厘米,B'C'=24厘米.求:BC、AC、A'B'、A'C'.
C'
B'
A'
C
B
A
解:因为△ABC~△A'B'C'
所以
=
=
AB
BC
A'B'
B'C'
60
72
又 AB=15厘米 B'C'=24厘米
所以 A'B'=18厘米 BC=20厘米
故 AC=60–15–20=25(厘米)
A'C'=72–18–24=30(厘米)
例.如图,在正方形网格上有△A1B1C1和△A2B2C2 ,这两个三角形相似吗?
如果相似,求出△A1B1C1和△A2B2C2的面积比.
2 : 1
解:相似.
因为相似比是
所以面积比是
4 : 1
1、两个相似三角形的相似比为1 ∶3,它们的对应高的比是 .
2、两个相似三角形的相似比为2∶3,它们的对应中线的比是 .
3、两个相似三角形的对应高的比为3∶5,它们的对角平分线的比是 .
4、两个相似三角形的对应中线的比为9∶16,它们的相似比是 .
5、两个相似三角形的对应角平分线的比为4∶9,它们的对应高的比是 .
1∶3
2∶3
3∶5
9∶16
4∶9
课堂练习
6.把一个三角形变成和它相似的三角形,
(1)如果边长扩大为原来的5倍,那么面积扩大为原来的__________倍.
(2)如果面积扩大为原来的100倍,那么边长扩大为原来的__________倍.
7.两个相似三角形的一对对应边分别是35厘米和14 厘米,(1)它们的周长差60厘米,这两个三角形的周长分别是________________.(2)它们的面积之和是58平方厘米,这两个三角形的面积分别是______________.
25
10
100cm、40cm
50cm2、8cm2
1、相似三角形对应边成______, 对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
相似比的平方
相似三角形的性质
比例
相等
相似比
相似比
归纳新知
1.若△ABC∽△DEF,相似比为3∶1,则△ABC与△DEF对应的高线之比为( )
A.1∶3 B.3∶1
C.9∶1 D.1∶9
B
课后练习
2.如图,△ABC∽△A′B′C′,AD和A′D′分别是△ABC和△A′B′C′的高,若AD=2,A′D′=3,则△ABC与△A′B′C′的相似比为_________
2∶3
3.(练习2变式)如图,点D,E分别在△ABC的AB,AC边上,且DE∥BC,AG⊥BC于点G,与DE交于点F.已知,BC=10,AF=3.FG=2,求DE的长.
4.已知△ABC∽△DEF,相似比为3∶2,则△ABC与△DEF的对应角平分线之比为( )
A.3∶4 B.2∶3
C.9∶16 D.3∶2
5.已知△ABC∽△DEF,且△ABC与△DEF的角平分线之比为3∶2,△ABC的最短边为4.5 cm,则△DEF的最短边为( )
A.6 cm B.2 cm C.3 cm D.4 cm
D
C
6.(原创题)如图,D,E,F分别是△ABC的边BC,AB,AC上的点,EF∥BC,AD平分∠BAC与EF相交于点G,AD=10,DG=5,BC=8.则EF=____.
4
C
8.(2019·沈阳)已知△ABC∽△A′B′C′,AD和A′D′是它们的对应中线,若AD=10,A′D′=6,则AB∶A′B′=________.
5∶3
B
11.如果△ABC∽△DEF,点A,B,C的对应点分别是D,E,F,△ABC的三边长上的中线为3,4,6,△DEF的一边上的中线长为12,那么△DEF的三边上的中线之和不可能是( )
A.65
B.52
C.39
D.26
A
12.如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在河的北岸边每隔50米有一根电线杆,小丽站在离岸边15米的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且这两棵树之间还有三棵树,则河宽________米.
22.5
13.如图,在△ABC中,D,E分别是△ABC的AB,AC边上的点,DE∥BC,CF,EG分别是△ABC与△ADE的中线,已知AD∶DB=4∶3,AB=18 cm,EG=4 cm,求CF的长.
(1)求证:△AEH∽△ABC;
(2)求矩形EFGH的面积.
(1)证明:∵四边形EFGH是矩形,∴EH∥BC,∴△AEH∽△ABC
湘教版· 数学· 九年级(上)
3.4.2 相似三角形的性质
第三章 图形的相似
理解掌握相似三角形对应线段(高、中线、角平分线)及相似三角形的面积、周长比与相似比之间的关系。
学习目标
相似三角形的———————, 各对应边——————.
对应角相等
成比例
1.三角形相似的判定方法有那些?
两个角对应相等的两个三角形相似.
两边对应成比例且夹角相等的两个三角形相似 .
三边对应成比例的两个三角形相似.
2. 相似三角形的有哪些性质?
3.相似三角形还有哪些性质?
复习导入
思考
两个三角形相似,除了对应边成比例、对应角相等之外,还可以得到许多有用的结果.例如,在图中,△ABC和 △A′B′C′ 是两个相似三角形,相似比为k,其中AD、B′C′分别为BC、A′D′边上的高,那么AD、 A′D′之间有什么关系?
两角对应相等,两三角形相似
∽
∽
已知
所以∠B=∠B′( )
相似三角形的对应角相等
∽
( )
相似三角形的性质
结论:相似三角形对应高的比等于相似比
合作探究
问题2:如图, △ABC∽△ A′B′C′,相似比为K, AD 、 A′D′分别是BC 、 B′C′边上的中线.问:AD 、 A′D′之间有什么关系?
D'
C'
B'
A'
D
C
B
A
因为△ABC∽△ A′B′C′
所以
又
又 ∠B=∠B′
所以 △ABD∽△ A′B′D′
所以
结论:相似三角形对应中线的比等于相似比
解
所以
A′
C′
B′
C
B
A
E′
E
∽
类似结论
自主思考---
结论:相似三角形对应角的角平分线的比等于相似比.
问题:4
图中(1)、(2)、(3)分别是边长为1、2、3的等边三角形,相似吗?
(2)与(1)的相似比=____,
(2)与(1)的面积比=____;周长比=
(3)与(1)的相似比=_ __,
(3)与(1)的面积比= ___;周长比=
A
B
C
A’
B’
C’
如图,已知△ABC∽△A′B′C′,相似比为k,则△ABC与△A′B′C′的周长比和面积比分别等于什么?怎么来说明?
A
B
C
A'
B'
C'
相似三角形的周长比等于相似比吗?
从而由等比性质有
结论:相似三角形的周长比等于相似比.
已知:如图, △ABC∽△A’B’C’,它们的相似比是K,
AD、A’D’分别是高.
求证:
证明: ∵△ABC∽△A’B’C’
B’
D’
C’
A’
A
B
C
D
结论:相似三角形的面积比等于相似比的平方.
通过前面的思考、探索、推理,我们得到相似三角形有如下性质;
相似三角形对应高的比、对应中线的比、对应角平分线的比、周长的比等于相似比.
相似三角形面积的比等于相似比的平方.
归纳总结:
已知△ABC∽△A′B′C′,相似比为2:3.
(1)如果AD,A′D′分别为这两个三角形的对应高,且AD=9cm,求A′D′的长.
(2)如果AE,A′E′分别为这两个三角形的对应中线,且A′E′=9cm,求AE的长.
(3)如果AF,A′F′分别为这两个三角形的对应角平分线,求 的值.
例: 如图,△ABC~△A'B'C',它们的周长分别是60厘米和72厘米,且AB=15厘米,B'C'=24厘米.求:BC、AC、A'B'、A'C'.
C'
B'
A'
C
B
A
解:因为△ABC~△A'B'C'
所以
=
=
AB
BC
A'B'
B'C'
60
72
又 AB=15厘米 B'C'=24厘米
所以 A'B'=18厘米 BC=20厘米
故 AC=60–15–20=25(厘米)
A'C'=72–18–24=30(厘米)
例.如图,在正方形网格上有△A1B1C1和△A2B2C2 ,这两个三角形相似吗?
如果相似,求出△A1B1C1和△A2B2C2的面积比.
2 : 1
解:相似.
因为相似比是
所以面积比是
4 : 1
1、两个相似三角形的相似比为1 ∶3,它们的对应高的比是 .
2、两个相似三角形的相似比为2∶3,它们的对应中线的比是 .
3、两个相似三角形的对应高的比为3∶5,它们的对角平分线的比是 .
4、两个相似三角形的对应中线的比为9∶16,它们的相似比是 .
5、两个相似三角形的对应角平分线的比为4∶9,它们的对应高的比是 .
1∶3
2∶3
3∶5
9∶16
4∶9
课堂练习
6.把一个三角形变成和它相似的三角形,
(1)如果边长扩大为原来的5倍,那么面积扩大为原来的__________倍.
(2)如果面积扩大为原来的100倍,那么边长扩大为原来的__________倍.
7.两个相似三角形的一对对应边分别是35厘米和14 厘米,(1)它们的周长差60厘米,这两个三角形的周长分别是________________.(2)它们的面积之和是58平方厘米,这两个三角形的面积分别是______________.
25
10
100cm、40cm
50cm2、8cm2
1、相似三角形对应边成______, 对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
相似比的平方
相似三角形的性质
比例
相等
相似比
相似比
归纳新知
1.若△ABC∽△DEF,相似比为3∶1,则△ABC与△DEF对应的高线之比为( )
A.1∶3 B.3∶1
C.9∶1 D.1∶9
B
课后练习
2.如图,△ABC∽△A′B′C′,AD和A′D′分别是△ABC和△A′B′C′的高,若AD=2,A′D′=3,则△ABC与△A′B′C′的相似比为_________
2∶3
3.(练习2变式)如图,点D,E分别在△ABC的AB,AC边上,且DE∥BC,AG⊥BC于点G,与DE交于点F.已知,BC=10,AF=3.FG=2,求DE的长.
4.已知△ABC∽△DEF,相似比为3∶2,则△ABC与△DEF的对应角平分线之比为( )
A.3∶4 B.2∶3
C.9∶16 D.3∶2
5.已知△ABC∽△DEF,且△ABC与△DEF的角平分线之比为3∶2,△ABC的最短边为4.5 cm,则△DEF的最短边为( )
A.6 cm B.2 cm C.3 cm D.4 cm
D
C
6.(原创题)如图,D,E,F分别是△ABC的边BC,AB,AC上的点,EF∥BC,AD平分∠BAC与EF相交于点G,AD=10,DG=5,BC=8.则EF=____.
4
C
8.(2019·沈阳)已知△ABC∽△A′B′C′,AD和A′D′是它们的对应中线,若AD=10,A′D′=6,则AB∶A′B′=________.
5∶3
B
11.如果△ABC∽△DEF,点A,B,C的对应点分别是D,E,F,△ABC的三边长上的中线为3,4,6,△DEF的一边上的中线长为12,那么△DEF的三边上的中线之和不可能是( )
A.65
B.52
C.39
D.26
A
12.如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在河的北岸边每隔50米有一根电线杆,小丽站在离岸边15米的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且这两棵树之间还有三棵树,则河宽________米.
22.5
13.如图,在△ABC中,D,E分别是△ABC的AB,AC边上的点,DE∥BC,CF,EG分别是△ABC与△ADE的中线,已知AD∶DB=4∶3,AB=18 cm,EG=4 cm,求CF的长.
(1)求证:△AEH∽△ABC;
(2)求矩形EFGH的面积.
(1)证明:∵四边形EFGH是矩形,∴EH∥BC,∴△AEH∽△ABC
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
