北师大版七上数学5.5.1 产品配套问题与工程问题课件(共30张)
文档属性
| 名称 | 北师大版七上数学5.5.1 产品配套问题与工程问题课件(共30张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 22:15:16 | ||
图片预览











文档简介
(共30张PPT)
第五章
一元一次方程
5.5
应用一元一次方程——“希望工程”义演
第1课时
产品配套与工程问题
1
课堂讲解
配套问题
工程问题
2
课时流程
逐点
导讲练
课堂小结
作业提升
1
知识点
配套问题
知1-讲
1.调配问题包括调动和配套两种问题.
2.调动问题:指从甲处调一些人(或物)到乙处,使之符
合一定的数量关系,或从第三方调入一些人(或物)到
甲、乙两处,使之符合一定的数量关系,
其基本的等量关系为:甲人(或物)数+乙人(或物)数
=总人(或物)数.
知1-讲
例1
学校组织植树活动,已知在甲处植树的有23人,
在乙处植树的有17人.现调20人去支援,使在
甲处植树的人数是在乙处植树人数的2倍.应
调往甲、乙两处各多少人?
导引:此类问题多用列表法找等量关系.设应调往甲
处x人,列表如下:
原有人数
增加人数
现有人数
甲处
23
x
23+x
乙处
17
20-x
17+(20-x)
知1-讲
解:设应调往甲处x人,则调往乙处(20-x)人,
根据题意,得
×(23+x)=17+(20-x),
解得x=17.
20-x=3.
答:应调往甲处17人,调往乙处3人.
总
结
知1-讲
用列表法把调配前后的人(物)数表示出来,
可以较方便地找到等量关系,也锻炼了同学们将
已知条件转化成数学语言的能力,体现了数学中
的转化思想.
知1-讲
配套问题:已知总人数,分成几部分分别从事
不同项目,各项目数量之间的比例符合总体要
求.关键是弄清配套双方的数量关系.
知1-讲
例2
某车间有28名工人,生产一种螺栓和螺帽,平
均每人每小时能生产螺栓12个或螺帽18个,两
个螺栓要配3个螺帽.应安排多少名工人生产
螺栓,多少名工人生产螺帽,才能使生产的螺
栓和螺帽刚好配套?
导引:本题的等量关系为:生产的螺栓数×3=生产
的螺帽数×2,故可设应安排x名工人生产螺栓,
用含x的式子分别表示出螺栓和螺帽的数量,
再列方程求解.
知1-讲
解:设应安排x名工人生产螺栓,
则(28-x)名工人生产螺帽.
根据题意,得3×12x=2×18(28-x),
解得x=14.
所以28-x=14.
答:应安排14名工人生产螺栓,14名工人生产
螺帽,才能使生产的螺栓和螺帽刚好配套.
知1-讲
总
结
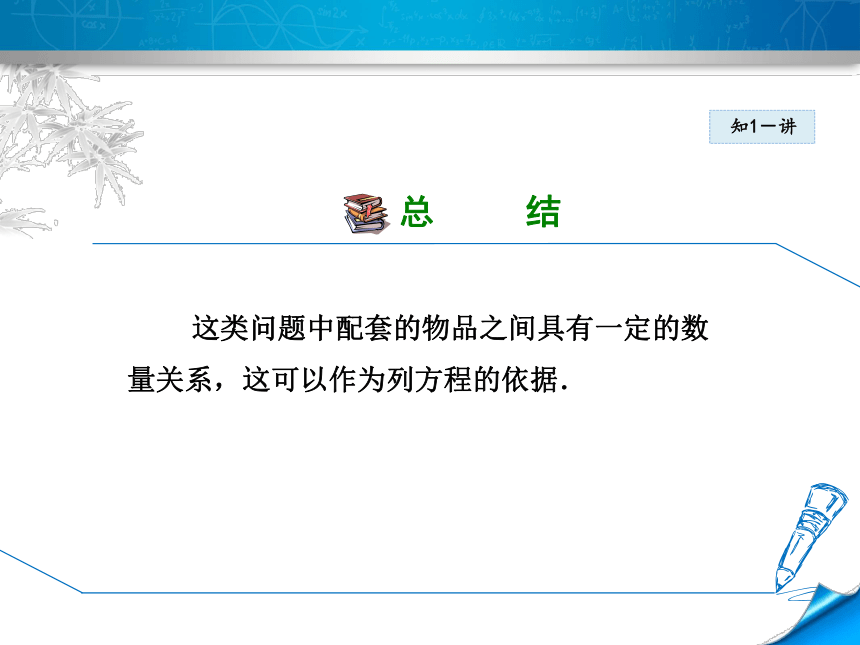
这类问题中配套的物品之间具有一定的数
量关系,这可以作为列方程的依据.
知1-练
41人参加运土劳动,有30根扁担,安排多少人抬,多少人挑,可使扁担和人数相配不多不少?若设有x人挑土,则可列方程为( )
A.2x-(30-x)=41 B.
+(41-x)=30
C.x+
=30
D.30-x=41-x
1
C
知1-练
在加固某段河坝时,需要动用15台挖土、运土机械,每台机械每小时能挖土18
m3或运土12
m3,为了使挖出的土能及时运走,若安排x台机械挖土,则可列方程为( )
A.18x-12x=15
B.18x=12(15-x)
C.12x=18(15-x)
D.18x+12x=15
2
B
知1-练
某车间有28名工人,每人每天能生产螺栓12个或螺母18个,设有x名工人生产螺栓,每天生产的螺栓和螺母按1∶2配套,则所列方程正确的是( )
A.12x=18(28-x)
B.18x=12(28-x)
C.2×12x=18(28-x)
D.2×18x=12(28-x)
3
C
2
知识点
工程问题
知2-导
一件工作,甲单独做20小时完成,乙单独做12小
时完成,那么两人合作多少小时完成?
思考:甲每小时完成全部工作的______;
乙每小时完成全部工作的_______;
甲x小时完成全部工作的_______;
乙x小时完成全部工作的_______.
知2-讲
1.基本关系式:工作量=工作效率×工作时间,
工作时间=
,工作效率=
.
2.当问题中总工作量未知而又不求总工作量时,
要把总工作量看作整体1.
知2-讲
3.常见的等量关系为:总工作量=各部分工作量之和.
4.找等量关系的方法与行程问题相类似,一般有如下
规律:在工作量、工作效率、工作时间这三个量中,
如果甲量已知,从乙量设元,那么就从丙量找等量
关系列方程.
知2-讲
例3
一个水池有甲、乙、丙三个水管,甲、乙是
进水管,丙是出水管,单开甲管20
min可将水
池注满,单开乙管15
min可将水池注满,单开
丙管25
min可将满池水放完.现在先开甲、
乙两管,4
min后关上甲管开丙管,问又经过
多少分钟才能将水池注满.
知2-讲
导引:弄清本例题意,必须明确两点:(1)在一些工程问
题中,工作量未知而又不求工作量时,我们常常
把工作量看作整体“1”;(2)设又经过x分钟才能
将水池注满,列表如下:
工作量
工作效率
工作时间/min
甲
×4
4
乙
(4+x)
4+x
丙
x
x
知2-讲
相等关系:甲注水量+乙注水量-丙放水量=1.
解:设又经过x
min才能将水池注满,
根据题意得:
×4+
(4+x)-
x=1,
解得x=20.
答:又经过20
min才能将水池注满.
总
结
知2-讲
本例中等量关系的实质是:
(1)总工作量等于各
部分工作量之和;(2)要把丙工作量看作为“-”
工作量.
知2-讲
例4
刺绣一件作品,甲单独绣需要15天完成,乙
单独绣需要12天完成.现在甲先单独绣1天,
接着乙又单独绣4天,剩下的工作由甲、乙
两人合绣.问再绣多少天可以完成这件作品?
解:设再绣x天可以完成这件作品.
由题意,得
解得x=4.
答:再绣4天可以完成这件作品.
知2-讲
(中考·长沙)某工程队承包了某段全长1
755
m的过江隧道施工任务,甲、乙两个班组分别从东、西两端同时掘进.已知甲组比乙组平均每天多掘进0.6
m,经过5天施工,两组共掘进了45
m.
(1)求甲、乙两个班组平均每天各掘进多少米.
(2)为加快进度,通过改进施工技术,在剩余的工程中,
甲组平均每天能比原来多掘进0.2
m,乙组平均每
天能比原来多掘进0.3
m.按此施工进度,能够比
原来少用多少天完成任务?
例5
知2-讲
解:(1)设乙班组平均每天掘进x
m,则甲班组平均
每天掘进(x+0.6)
m.
根据题意,得5x+5(x+0.6)=45.
解得x=4.2.则x+0.6=4.8.
答:甲班组平均每天掘进4.8
m,乙班组平
均每天掘进4.2
m.
(2)改进施工技术后,甲班组平均每天掘进4.8
+0.2=5(m);乙班组平均每天掘进4.2+0.3
=4.5(m).
知2-讲
改进施工技术后,剩余的工程所用时间为
(1
755-45)÷(5+4.5)=180(天).
按原来速度,剩余的工程所用时间为
(1
755-45)÷(4.8+4.2)=190(天).
少用天数为190-180=10(天).
答:能够比原来少用10天完成任务.
知2-练
某工人原计划每天生产a个零件,现在实际每天多生产b个零件,则生产m个零件提前的天数为( )
A.
B.
C.
D.
1
B
知2-练
某项工作甲单独做4天完成,乙单独做6天完成,若甲先干1天,然后甲、乙合作完成此项工程,若设甲一共做了x天,则所列方程为( )
A.
B.
C.
D.
2
C
知2-练
一个水池有甲、乙两个水龙头,单独开甲水龙头,4
h可把空水池灌满,单独开乙水龙头,6
h可把
满池水放完,如果要灌满水池的
,且同时打开甲、乙两水龙头,则需要的时间是( )
A.4
h
B.
h
C.8
h
D.
h
3
C
解决配套问题时,要弄清配套双方的数量关系,
准确地找出题中的相等关系;
调动问题的基本相等关系为:
甲人(或物)数+乙人(或物)数=总人(或物)数.
1.工作问题的基本量:工作量、工作效率、工作时
间,基本关系式:工作量=工作效率×工作时间.
2.当工作总量未给出具体数量时,常把工作总量当作
整体1.常用的相等关系为:工作总量=各部分工作
量的和.
1.必做:
完成教材P153,复习题T7-9
第五章
一元一次方程
5.5
应用一元一次方程——“希望工程”义演
第1课时
产品配套与工程问题
1
课堂讲解
配套问题
工程问题
2
课时流程
逐点
导讲练
课堂小结
作业提升
1
知识点
配套问题
知1-讲
1.调配问题包括调动和配套两种问题.
2.调动问题:指从甲处调一些人(或物)到乙处,使之符
合一定的数量关系,或从第三方调入一些人(或物)到
甲、乙两处,使之符合一定的数量关系,
其基本的等量关系为:甲人(或物)数+乙人(或物)数
=总人(或物)数.
知1-讲
例1
学校组织植树活动,已知在甲处植树的有23人,
在乙处植树的有17人.现调20人去支援,使在
甲处植树的人数是在乙处植树人数的2倍.应
调往甲、乙两处各多少人?
导引:此类问题多用列表法找等量关系.设应调往甲
处x人,列表如下:
原有人数
增加人数
现有人数
甲处
23
x
23+x
乙处
17
20-x
17+(20-x)
知1-讲
解:设应调往甲处x人,则调往乙处(20-x)人,
根据题意,得
×(23+x)=17+(20-x),
解得x=17.
20-x=3.
答:应调往甲处17人,调往乙处3人.
总
结
知1-讲
用列表法把调配前后的人(物)数表示出来,
可以较方便地找到等量关系,也锻炼了同学们将
已知条件转化成数学语言的能力,体现了数学中
的转化思想.
知1-讲
配套问题:已知总人数,分成几部分分别从事
不同项目,各项目数量之间的比例符合总体要
求.关键是弄清配套双方的数量关系.
知1-讲
例2
某车间有28名工人,生产一种螺栓和螺帽,平
均每人每小时能生产螺栓12个或螺帽18个,两
个螺栓要配3个螺帽.应安排多少名工人生产
螺栓,多少名工人生产螺帽,才能使生产的螺
栓和螺帽刚好配套?
导引:本题的等量关系为:生产的螺栓数×3=生产
的螺帽数×2,故可设应安排x名工人生产螺栓,
用含x的式子分别表示出螺栓和螺帽的数量,
再列方程求解.
知1-讲
解:设应安排x名工人生产螺栓,
则(28-x)名工人生产螺帽.
根据题意,得3×12x=2×18(28-x),
解得x=14.
所以28-x=14.
答:应安排14名工人生产螺栓,14名工人生产
螺帽,才能使生产的螺栓和螺帽刚好配套.
知1-讲
总
结
这类问题中配套的物品之间具有一定的数
量关系,这可以作为列方程的依据.
知1-练
41人参加运土劳动,有30根扁担,安排多少人抬,多少人挑,可使扁担和人数相配不多不少?若设有x人挑土,则可列方程为( )
A.2x-(30-x)=41 B.
+(41-x)=30
C.x+
=30
D.30-x=41-x
1
C
知1-练
在加固某段河坝时,需要动用15台挖土、运土机械,每台机械每小时能挖土18
m3或运土12
m3,为了使挖出的土能及时运走,若安排x台机械挖土,则可列方程为( )
A.18x-12x=15
B.18x=12(15-x)
C.12x=18(15-x)
D.18x+12x=15
2
B
知1-练
某车间有28名工人,每人每天能生产螺栓12个或螺母18个,设有x名工人生产螺栓,每天生产的螺栓和螺母按1∶2配套,则所列方程正确的是( )
A.12x=18(28-x)
B.18x=12(28-x)
C.2×12x=18(28-x)
D.2×18x=12(28-x)
3
C
2
知识点
工程问题
知2-导
一件工作,甲单独做20小时完成,乙单独做12小
时完成,那么两人合作多少小时完成?
思考:甲每小时完成全部工作的______;
乙每小时完成全部工作的_______;
甲x小时完成全部工作的_______;
乙x小时完成全部工作的_______.
知2-讲
1.基本关系式:工作量=工作效率×工作时间,
工作时间=
,工作效率=
.
2.当问题中总工作量未知而又不求总工作量时,
要把总工作量看作整体1.
知2-讲
3.常见的等量关系为:总工作量=各部分工作量之和.
4.找等量关系的方法与行程问题相类似,一般有如下
规律:在工作量、工作效率、工作时间这三个量中,
如果甲量已知,从乙量设元,那么就从丙量找等量
关系列方程.
知2-讲
例3
一个水池有甲、乙、丙三个水管,甲、乙是
进水管,丙是出水管,单开甲管20
min可将水
池注满,单开乙管15
min可将水池注满,单开
丙管25
min可将满池水放完.现在先开甲、
乙两管,4
min后关上甲管开丙管,问又经过
多少分钟才能将水池注满.
知2-讲
导引:弄清本例题意,必须明确两点:(1)在一些工程问
题中,工作量未知而又不求工作量时,我们常常
把工作量看作整体“1”;(2)设又经过x分钟才能
将水池注满,列表如下:
工作量
工作效率
工作时间/min
甲
×4
4
乙
(4+x)
4+x
丙
x
x
知2-讲
相等关系:甲注水量+乙注水量-丙放水量=1.
解:设又经过x
min才能将水池注满,
根据题意得:
×4+
(4+x)-
x=1,
解得x=20.
答:又经过20
min才能将水池注满.
总
结
知2-讲
本例中等量关系的实质是:
(1)总工作量等于各
部分工作量之和;(2)要把丙工作量看作为“-”
工作量.
知2-讲
例4
刺绣一件作品,甲单独绣需要15天完成,乙
单独绣需要12天完成.现在甲先单独绣1天,
接着乙又单独绣4天,剩下的工作由甲、乙
两人合绣.问再绣多少天可以完成这件作品?
解:设再绣x天可以完成这件作品.
由题意,得
解得x=4.
答:再绣4天可以完成这件作品.
知2-讲
(中考·长沙)某工程队承包了某段全长1
755
m的过江隧道施工任务,甲、乙两个班组分别从东、西两端同时掘进.已知甲组比乙组平均每天多掘进0.6
m,经过5天施工,两组共掘进了45
m.
(1)求甲、乙两个班组平均每天各掘进多少米.
(2)为加快进度,通过改进施工技术,在剩余的工程中,
甲组平均每天能比原来多掘进0.2
m,乙组平均每
天能比原来多掘进0.3
m.按此施工进度,能够比
原来少用多少天完成任务?
例5
知2-讲
解:(1)设乙班组平均每天掘进x
m,则甲班组平均
每天掘进(x+0.6)
m.
根据题意,得5x+5(x+0.6)=45.
解得x=4.2.则x+0.6=4.8.
答:甲班组平均每天掘进4.8
m,乙班组平
均每天掘进4.2
m.
(2)改进施工技术后,甲班组平均每天掘进4.8
+0.2=5(m);乙班组平均每天掘进4.2+0.3
=4.5(m).
知2-讲
改进施工技术后,剩余的工程所用时间为
(1
755-45)÷(5+4.5)=180(天).
按原来速度,剩余的工程所用时间为
(1
755-45)÷(4.8+4.2)=190(天).
少用天数为190-180=10(天).
答:能够比原来少用10天完成任务.
知2-练
某工人原计划每天生产a个零件,现在实际每天多生产b个零件,则生产m个零件提前的天数为( )
A.
B.
C.
D.
1
B
知2-练
某项工作甲单独做4天完成,乙单独做6天完成,若甲先干1天,然后甲、乙合作完成此项工程,若设甲一共做了x天,则所列方程为( )
A.
B.
C.
D.
2
C
知2-练
一个水池有甲、乙两个水龙头,单独开甲水龙头,4
h可把空水池灌满,单独开乙水龙头,6
h可把
满池水放完,如果要灌满水池的
,且同时打开甲、乙两水龙头,则需要的时间是( )
A.4
h
B.
h
C.8
h
D.
h
3
C
解决配套问题时,要弄清配套双方的数量关系,
准确地找出题中的相等关系;
调动问题的基本相等关系为:
甲人(或物)数+乙人(或物)数=总人(或物)数.
1.工作问题的基本量:工作量、工作效率、工作时
间,基本关系式:工作量=工作效率×工作时间.
2.当工作总量未给出具体数量时,常把工作总量当作
整体1.常用的相等关系为:工作总量=各部分工作
量的和.
1.必做:
完成教材P153,复习题T7-9
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
