黑龙江省鹤岗市绥滨县2020-2021学年九年级上学期期末考试数学试题(word版含答案)
文档属性
| 名称 | 黑龙江省鹤岗市绥滨县2020-2021学年九年级上学期期末考试数学试题(word版含答案) | 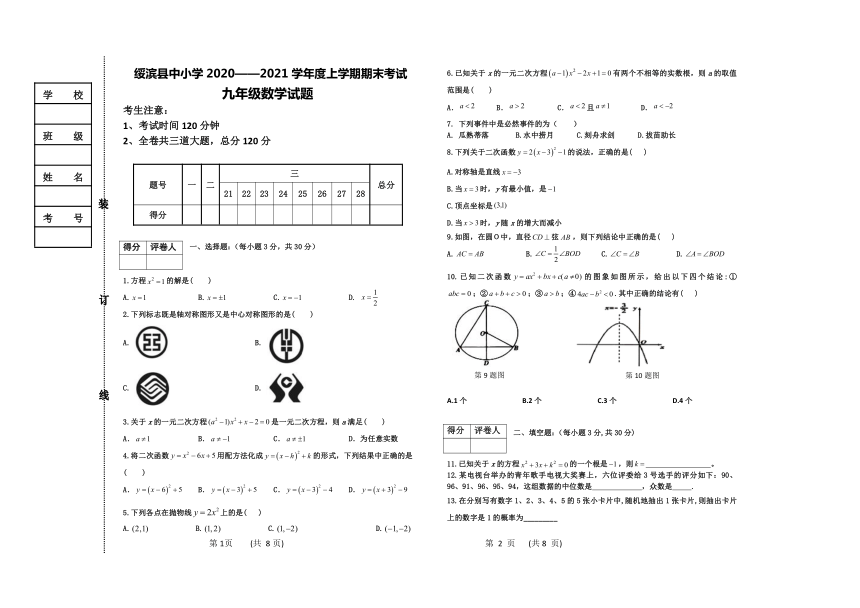 | |
| 格式 | zip | ||
| 文件大小 | 881.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 22:51:21 | ||
图片预览



文档简介
绥滨县中小学2020——2021学年度上学期期末考试
九年级数学试题
考生注意:
1、考试时间120分钟
2、全卷共三道大题,总分120分
学
校
班
级
姓
名
考
号
题号
一
二
三
总分
21
22
23
24
25
26
27
28
得分
得分
评卷人
1、选择题:(每小题3分,共30分)
1.方程的解是(
)
A.
B.
C.
D.
2.下列标志既是轴对称图形又是中心对称图形的是(?
)
A.
B.
C.
D.
3.关于x的一元二次方程是一元二次方程,则a满足(
)
A.
B.
C.
D.为任意实数
4.将二次函数用配方法化成的形式,下列结果中正确的是(
)
A.
B.
C.
D.
5.下列各点在抛物线上的是(
)
A.
B.
C.
D.
6.已知关于x的一元二次方程有两个不相等的实数根,则a的取值范围是( )
A.
B.
C.且
D.
7.
下列事件中是必然事件的为(
)
A.
瓜熟蒂落
B.水中捞月
C.刻舟求剑
D.拔苗助长
8.下列关于二次函数的说法,正确的是(
)
A.对称轴是直线
B.当时,y有最小值,是
C.顶点坐标是
D.当时,y随x的增大而减小
9.如图,在圆O中,直径弦,则下列结论中正确的是(
)
A.
B.
C.
D.
10.已知二次函数的图象如图所示,给出以下四个结论:①;②;③;④.其中正确的结论有(
)
A.1个
B.2个
C.3个
D.4个
得分
评卷人
2、填空题:(每小题3分,共30分)
11.已知关于x的方程的一个根是,则
。
12.某电视台举办的青年歌手电视大奖赛上,六位评委给3号选手的评分如下:90、96、91、96、95、94,这组数据的中位数是
,众数是
.
13.在分别写有数字1、2、3、4、5的5张小卡片中,随机地抽出1张卡片,则抽出卡片上的数字是1的概率为_________
14.已知抛物线y=ax2+bx+c
(a≠0)
与x轴的两个交点的坐标分别是(-3,0),
(2,0),则方程ax2+bx+c=0(a≠0)的解是
__________.
15.若弧长为4π的扇形的圆心角为直角,则该扇形的半径为__________.
16.若函数
y=kx2+2x﹣1
的图象与
x
轴仅有一个公共点,则常数
k
的值为__________.
17.已知二次函数y=(x
-
m)2当x
时,y随x的增大而减小,则m的取值范围是__________.
18.已知一个直角三角形的两条直角边的长恰好是方程x2-7x+12=0的两个实数根,则该直角三角形斜边上的中线长是__________.
19.
已知⊙P的半径为2,圆心P在抛物线y=
x2-1上运动,当⊙P与x轴相切时,圆心P的坐标为__________.
20.
在平面直角坐标系XOY中,正方形ABCD的位置如下图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第1个正方形的面积为________;第n个正方形的面积为__________.
三、解答题(共60分)
得分
评卷人
21.解方程(本题满分5分
)
(1)x2-6x=-9
(2)
(x+1)2=6x+6
得分
评卷人
22.(本题满分6分)
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别
为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
(1)
将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A1B1C1;
直接写出B1坐标为
。
(2)求出点B旋转到点B1所经过的路径长.
得分
评卷人
23.
(本题满分6分)
已知二次函数的图象如图所示,它与x轴的一个交点的坐标为
(-1,0),与y轴的交点坐标为(0,-3).
(1)求此二次函数的解析式;
(2)求此二次函数的图象与x轴的另一个交点的坐标;
(3)根据图象回答:当x取何值时,y<0?
得分
评卷人
24.
(本题满分7分)
某校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
1.
这次被调查的同学共有多少名?
2.把条形统计图补充完整;
3.校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供人用一餐.据此估算,该校名学生一餐浪费的食物可供多少人食用一餐?
得分
评卷人
25.(本题满分8分)
如图,AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD,CD∥AB.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为1,求图中阴影部分的面积(结果保留π).
得分
评卷人
26.
(本题满分8分)
现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果平均每人每月最多可投递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
得分
评卷人
27.(本题满分10分)
已知∠AOB=90°,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA,OB(或它们的反向延长线)相交于点D,E.
(1)当三角板绕点C旋转到CD与OA垂直时(如图①),易证:OD+OE=OC;
(2)当三角板绕点C旋转到CD与OA不垂直时,即在图②,图③这两种情况下,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段OD,OE,OC之间又有怎样的数量关系?请写出你的猜想,不需证明.
得分
评卷人
28.(
本题满分10分)
为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:
y=-2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?
最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
绥滨县2020——2021学年度上学期期末考试
九年级数学试题答案
1、填空题(每题3分)
1、B
2、A
3、C
4、C
5、B
6、C
7、A
8、B
9、B
10、C
二、选择题(每小题3分,共30分)(可酌情给分)
11.
12.
94.5
96
13.
14.
X1=-3
x2=2
15.8
16.k=0或k=-1
17.
18.2.5
19.
20.
5;
三、解答题(共60分)(解答题如有不同解法,可酌情给分)
21.计算(本题满分5分)
解:(1)原方程可变形为.
则
…………
(1分)
…………
(1分)
(2)原方程可变形为(x-5)(x+1)=0
…………
(2分)
∴x1=-1
x2=5
…………
(1分)
22.(本题满分6分)
解:(1)画图
…………(2分);
B1(-2,4)
…………(1分)
(2)OB==2,
…………1分
点B旋转到点B1所经过的路径长为=π.
…………(2分)
23.(本题满分6分)
解:
(1)由二次函数的图象经过(-1,0)和(0,-3)两点,
得
…………(1分)
解这个方程组,得
…………(1分)
∴抛物线的解析式为
…………(1分)
(2)令,得.
解这个方程,得,
…………(1分)
∴此二次函数的图象与x轴的另一个交点的坐标为(3,0).
…………(1分)
(3)当时,y<0.
…………(1分)
24.(本题满分7分)
1.这次被调查的同学共有
(名)
…………(2分)
2.剩少量的人数是:
(人)
…………(2分)
补图如下:
…………(1分)
3.
(人)
…………(1分)
答:该校一餐浪费的食物可供人食用一餐.
…………(1分)
25.(本题满分8分)
解:(1)直线CD与⊙O相切.
……1分
理由如下:
如图,连接OD.
∵OA=OD,∠DAB=45°,∴∠ODA=45°.
∴∠AOD=90°.
……2分
又∵CD∥AB,
∴∠ODC=∠AOD=90°,即OD⊥CD.
又∵点D在⊙O上,
∴直线CD与⊙O相切.
…………(1分)
(2)∵BC∥AD,CD∥AB,
∴
四边形ABCD是平行四边形.∴CD=AB=2.
…………(1分)
∴S梯形OBCD===.…………(1分)
∴图中阴影部分的面积=S梯形OBCD-S扇形OBD=-×π×12=-.…………(2分)
26.(本题满分8分)
解:(1)设该快递公司投递总件数的月平均增长率为x,…………(1分)
根据题意得10(1+x)2=12.1,
…………
(2分)
解得x1=0.1,x2=﹣2.1(不合题意舍去).
…………
(1分)
答:该快递公司投递总件数的月平均增长率为10%;
…………
(1分)
(2)今年6月份的快递投递任务是12.1×(1+10%)=13.31(万件).…………
(1分)
∵平均每人每月最多可投递0.6万件,
∴21名快递投递业务员能完成的快递投递任务是:0.6×21=12.6<13.31,
∴该公司现有的21名快递投递业务员不能完成今年6月份的快递投递任务
…………(1分)
∴需要增加业务员(13.31﹣12.6)÷0.6=≈2(人).
答:该公司现有的21名快递投递业务员不能完成今年6月份的快递投递任务,至少需要增加2名业务员.
…………(1分)
27.(本题满分10分)
解:图②中OD+OE=OC成立.
…………(2分)
证明:过点C分别作OA,OB的垂线,垂足分别为P,Q.
…………
(1分)
有△CPD≌△CQE,
…………
(3分)
∴DP=EQ,∵OP=OD+DP,OQ=OE-EQ,
又∵OP+OQ=OC,即OD+DP+OE-EQ=OC,∴OD+OE=OC.
…………(2分)
图③不成立,有数量关系:OE-OD=OC
…………
(2分)
28.(本题满分10分)
解:(1)由题意得w=(x-20)·y=(x-20)(-2x+80)=-2x2+120x-1600
故w与x的函数关系式为w=-2x2+120x-1600
…………(3分)
(2)w=-2x2+120x-1600=-2(x-30)2+200.
∵-2<0,∴当x=30时,w有最大值,w最大值为200
则该产品销售价定为每千克30元时,每天销售利润最大,最大销售利润为200元 …………
(4分)
(3)当w=150时,可得方程-2(x-30)2+200=150.
…………
(1分)
解得x1=25,x2=35.∵35>28,∴x2=35不符合题意,应舍去
…………
(1分)
则该农户想要每天获得150元的销售利润,销售价应定为每千克25元
…………
(1分)
第9题图
第10题图
第1页 (共
8页)
第
2
页
(共8
页)
九年级数学试题
考生注意:
1、考试时间120分钟
2、全卷共三道大题,总分120分
学
校
班
级
姓
名
考
号
题号
一
二
三
总分
21
22
23
24
25
26
27
28
得分
得分
评卷人
1、选择题:(每小题3分,共30分)
1.方程的解是(
)
A.
B.
C.
D.
2.下列标志既是轴对称图形又是中心对称图形的是(?
)
A.
B.
C.
D.
3.关于x的一元二次方程是一元二次方程,则a满足(
)
A.
B.
C.
D.为任意实数
4.将二次函数用配方法化成的形式,下列结果中正确的是(
)
A.
B.
C.
D.
5.下列各点在抛物线上的是(
)
A.
B.
C.
D.
6.已知关于x的一元二次方程有两个不相等的实数根,则a的取值范围是( )
A.
B.
C.且
D.
7.
下列事件中是必然事件的为(
)
A.
瓜熟蒂落
B.水中捞月
C.刻舟求剑
D.拔苗助长
8.下列关于二次函数的说法,正确的是(
)
A.对称轴是直线
B.当时,y有最小值,是
C.顶点坐标是
D.当时,y随x的增大而减小
9.如图,在圆O中,直径弦,则下列结论中正确的是(
)
A.
B.
C.
D.
10.已知二次函数的图象如图所示,给出以下四个结论:①;②;③;④.其中正确的结论有(
)
A.1个
B.2个
C.3个
D.4个
得分
评卷人
2、填空题:(每小题3分,共30分)
11.已知关于x的方程的一个根是,则
。
12.某电视台举办的青年歌手电视大奖赛上,六位评委给3号选手的评分如下:90、96、91、96、95、94,这组数据的中位数是
,众数是
.
13.在分别写有数字1、2、3、4、5的5张小卡片中,随机地抽出1张卡片,则抽出卡片上的数字是1的概率为_________
14.已知抛物线y=ax2+bx+c
(a≠0)
与x轴的两个交点的坐标分别是(-3,0),
(2,0),则方程ax2+bx+c=0(a≠0)的解是
__________.
15.若弧长为4π的扇形的圆心角为直角,则该扇形的半径为__________.
16.若函数
y=kx2+2x﹣1
的图象与
x
轴仅有一个公共点,则常数
k
的值为__________.
17.已知二次函数y=(x
-
m)2当x
时,y随x的增大而减小,则m的取值范围是__________.
18.已知一个直角三角形的两条直角边的长恰好是方程x2-7x+12=0的两个实数根,则该直角三角形斜边上的中线长是__________.
19.
已知⊙P的半径为2,圆心P在抛物线y=
x2-1上运动,当⊙P与x轴相切时,圆心P的坐标为__________.
20.
在平面直角坐标系XOY中,正方形ABCD的位置如下图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第1个正方形的面积为________;第n个正方形的面积为__________.
三、解答题(共60分)
得分
评卷人
21.解方程(本题满分5分
)
(1)x2-6x=-9
(2)
(x+1)2=6x+6
得分
评卷人
22.(本题满分6分)
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别
为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
(1)
将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A1B1C1;
直接写出B1坐标为
。
(2)求出点B旋转到点B1所经过的路径长.
得分
评卷人
23.
(本题满分6分)
已知二次函数的图象如图所示,它与x轴的一个交点的坐标为
(-1,0),与y轴的交点坐标为(0,-3).
(1)求此二次函数的解析式;
(2)求此二次函数的图象与x轴的另一个交点的坐标;
(3)根据图象回答:当x取何值时,y<0?
得分
评卷人
24.
(本题满分7分)
某校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
1.
这次被调查的同学共有多少名?
2.把条形统计图补充完整;
3.校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供人用一餐.据此估算,该校名学生一餐浪费的食物可供多少人食用一餐?
得分
评卷人
25.(本题满分8分)
如图,AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD,CD∥AB.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为1,求图中阴影部分的面积(结果保留π).
得分
评卷人
26.
(本题满分8分)
现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果平均每人每月最多可投递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
得分
评卷人
27.(本题满分10分)
已知∠AOB=90°,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA,OB(或它们的反向延长线)相交于点D,E.
(1)当三角板绕点C旋转到CD与OA垂直时(如图①),易证:OD+OE=OC;
(2)当三角板绕点C旋转到CD与OA不垂直时,即在图②,图③这两种情况下,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段OD,OE,OC之间又有怎样的数量关系?请写出你的猜想,不需证明.
得分
评卷人
28.(
本题满分10分)
为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:
y=-2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?
最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
绥滨县2020——2021学年度上学期期末考试
九年级数学试题答案
1、填空题(每题3分)
1、B
2、A
3、C
4、C
5、B
6、C
7、A
8、B
9、B
10、C
二、选择题(每小题3分,共30分)(可酌情给分)
11.
12.
94.5
96
13.
14.
X1=-3
x2=2
15.8
16.k=0或k=-1
17.
18.2.5
19.
20.
5;
三、解答题(共60分)(解答题如有不同解法,可酌情给分)
21.计算(本题满分5分)
解:(1)原方程可变形为.
则
…………
(1分)
…………
(1分)
(2)原方程可变形为(x-5)(x+1)=0
…………
(2分)
∴x1=-1
x2=5
…………
(1分)
22.(本题满分6分)
解:(1)画图
…………(2分);
B1(-2,4)
…………(1分)
(2)OB==2,
…………1分
点B旋转到点B1所经过的路径长为=π.
…………(2分)
23.(本题满分6分)
解:
(1)由二次函数的图象经过(-1,0)和(0,-3)两点,
得
…………(1分)
解这个方程组,得
…………(1分)
∴抛物线的解析式为
…………(1分)
(2)令,得.
解这个方程,得,
…………(1分)
∴此二次函数的图象与x轴的另一个交点的坐标为(3,0).
…………(1分)
(3)当时,y<0.
…………(1分)
24.(本题满分7分)
1.这次被调查的同学共有
(名)
…………(2分)
2.剩少量的人数是:
(人)
…………(2分)
补图如下:
…………(1分)
3.
(人)
…………(1分)
答:该校一餐浪费的食物可供人食用一餐.
…………(1分)
25.(本题满分8分)
解:(1)直线CD与⊙O相切.
……1分
理由如下:
如图,连接OD.
∵OA=OD,∠DAB=45°,∴∠ODA=45°.
∴∠AOD=90°.
……2分
又∵CD∥AB,
∴∠ODC=∠AOD=90°,即OD⊥CD.
又∵点D在⊙O上,
∴直线CD与⊙O相切.
…………(1分)
(2)∵BC∥AD,CD∥AB,
∴
四边形ABCD是平行四边形.∴CD=AB=2.
…………(1分)
∴S梯形OBCD===.…………(1分)
∴图中阴影部分的面积=S梯形OBCD-S扇形OBD=-×π×12=-.…………(2分)
26.(本题满分8分)
解:(1)设该快递公司投递总件数的月平均增长率为x,…………(1分)
根据题意得10(1+x)2=12.1,
…………
(2分)
解得x1=0.1,x2=﹣2.1(不合题意舍去).
…………
(1分)
答:该快递公司投递总件数的月平均增长率为10%;
…………
(1分)
(2)今年6月份的快递投递任务是12.1×(1+10%)=13.31(万件).…………
(1分)
∵平均每人每月最多可投递0.6万件,
∴21名快递投递业务员能完成的快递投递任务是:0.6×21=12.6<13.31,
∴该公司现有的21名快递投递业务员不能完成今年6月份的快递投递任务
…………(1分)
∴需要增加业务员(13.31﹣12.6)÷0.6=≈2(人).
答:该公司现有的21名快递投递业务员不能完成今年6月份的快递投递任务,至少需要增加2名业务员.
…………(1分)
27.(本题满分10分)
解:图②中OD+OE=OC成立.
…………(2分)
证明:过点C分别作OA,OB的垂线,垂足分别为P,Q.
…………
(1分)
有△CPD≌△CQE,
…………
(3分)
∴DP=EQ,∵OP=OD+DP,OQ=OE-EQ,
又∵OP+OQ=OC,即OD+DP+OE-EQ=OC,∴OD+OE=OC.
…………(2分)
图③不成立,有数量关系:OE-OD=OC
…………
(2分)
28.(本题满分10分)
解:(1)由题意得w=(x-20)·y=(x-20)(-2x+80)=-2x2+120x-1600
故w与x的函数关系式为w=-2x2+120x-1600
…………(3分)
(2)w=-2x2+120x-1600=-2(x-30)2+200.
∵-2<0,∴当x=30时,w有最大值,w最大值为200
则该产品销售价定为每千克30元时,每天销售利润最大,最大销售利润为200元 …………
(4分)
(3)当w=150时,可得方程-2(x-30)2+200=150.
…………
(1分)
解得x1=25,x2=35.∵35>28,∴x2=35不符合题意,应舍去
…………
(1分)
则该农户想要每天获得150元的销售利润,销售价应定为每千克25元
…………
(1分)
第9题图
第10题图
第1页 (共
8页)
第
2
页
(共8
页)
同课章节目录
