人教版七上数学3.1.2 等式的性质课件(共25张)
文档属性
| 名称 | 人教版七上数学3.1.2 等式的性质课件(共25张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 22:23:32 | ||
图片预览






文档简介
(共25张PPT)
第三章
一元一次方程
3.1
从算式到方程
第2课时
等式的性质
1
课堂讲解
等式的性质1
等式的性质2
用等式的性质解方程
2
课时流程
逐点
导讲练
课堂小结
课后作业
复习提问
引出问题
(1)什么叫做方程?
(2)什么叫做一元一次方程?
(3)一元一次方程有哪几个特征?
①只含有一个未知数;
②未知数的次数都是1;
③整式方程.
(4)请你举出一个一元一次方程的例子.
1
知识点
等式的性质1
知1-导
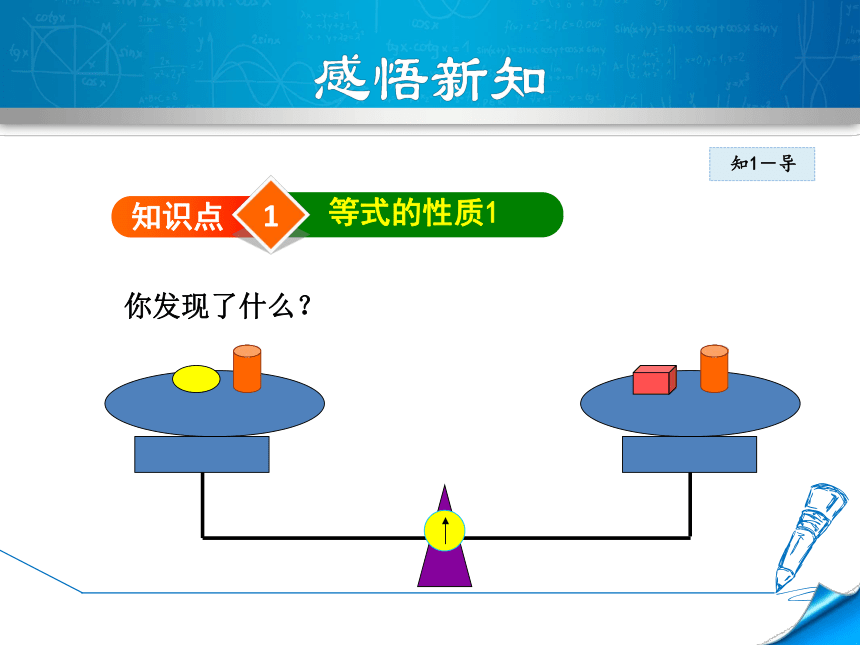
你发现了什么?
知1-导
你发现了什么?
知1-导
归
纳
(来自教材)
我们可以发现,如果在平衡的天平的两边都
加(或减)同样的量,天平还保持平衡.
知1-讲
等式的性质1:
等式两边加(或减)同一个数(或式子),结果仍相等,
用公式表示:如果a=b,那么a±c=b±c;
这里的a,b,c可以是具体的一个数,也可以是一
个代数式.
知1-讲
例1
根据等式的性质填空,并在后面的括号内填
上变形的根据.
(1)如果4x=x-2,那么4x-____=-2(
);
(2)如果2x+9=1,那么2x=1-____(
);
x
9
等式的性质1
等式的性质1
导引:(1)中方程的右边由x-2到-2,减了x,所以左边也
要减x;(2)中方程的左边由2x+9到2x,减了9,所
以右边也要减9.
知1-练
等式两边都加上(或__________)同一个__________(或________),结果仍相等;用字母表示:如果a=b,那么a±c=________.
1
若m+2n=p+2n,则m=________.依据是等式的性质________,它是将等式的两边______________.
2
减
数
式子
b±c
p
1
同时减去2n
知1-练
下列各种变形中,不正确的是( )
A.由2+x=5可得到x=5-2
B.由3x=2x-1可得到3x-2x=-1
C.由5x=4x+1可得到4x-5x=1
D.由6x-2x=-3可得到6x=2x-3
3
C
2
知识点
等式的性质2
知2-导
×3
÷
3
如:2=2
那么2×
3=2×3
如:6=6
那么6÷2=6÷2
知2-讲
等式的性质2:等式两边乘同一个数,或除以同一个
不为0的数,结果仍相等,用公式表示:如果a=b,
那么ac=bc,
(c≠0).
等式的性质2中,除以的同一个数不能为0.
知2-讲
例2
根据等式的性质填空,并在后面的括号内填
上变形的根据.
(1)如果-
=
,那么x=____(
);
(2)如果0.4a=3b,那么a=____(
).
等式的性质2
等式的性质2
导引:
(1)中方程的左边由-
到x,乘了-3,所以右边
也要乘-3;(2)中方程的左边由0.4a到a除以了0.4,
所以右边也要除以0.4,即乘
.
知2-练
等式2x-y=10变形为-4x+2y=-20的依据
为(
)
A.等式基本性质1
B.等式基本性质2
C.分数的基本性质
D.乘法分配律
1
B
知2-练
下列变形,正确的是(
)
A.如果a=b,那么
B.如果
,那么a=b
C.如果a2=3a,那么a=3
D.如果
-1=x,那么2x+1-1=3x
2
B
知2-练
已知x=y,下列各式:3x=3y,-2x=-2y,
=1,其中正确的有( )
A.1个
B.2个
C.3个
D.4个
3
C
知3-讲
3
知识点
用等式的性质解方程
例3
利用等式的性质解下列方程:
(1)
x+7
=
26;
(2)
-5x=20;
(3)
-5=4.
分析:要使方程x+7
=
26转化为x=a
(常数)的形式,
需去掉方程左边
的7,利用等式的性质1,方程
两边减7就得出x的值.你可以类似地考虑另两
个方程如何转化为x=a的形式.
知3-讲
解:(1)两边减7,得x+7-7=26-7.
于是x=19.
(2)两边除以-5,得
?
于是x=
-
4.
(3)两边加5,得
?
解以x为未知数的方程,就是把方程逐步转化为x=
a
(常
数)的形式,等式的性质是转化的重要依据.
(来自教材)
知3-讲
例4
若x=1是关于x的方程ax+b=c的解,求:
(1)(a+b-c)2的值;(2)
的值;
(3)|c-a-b-1|的值.
解:因为x=1是关于x的方程ax+b=c的解,
所以a+b=c.
(1)(a+b-c)2=[(a+b)-c]2=(c-c)2=0.
(2)
(3)|c-a-b-1|=|c-(a+b)-1|=|c-c-1|=1.
总
结
知3-讲
本例中a,b,c的值无法求出,表面上看似无
法求出相关式子的值,而运用整体思想就能达到求
解的目的.
知3-讲
例5
已知2x2+3x=5,求多项式-4x2-6x+6的值.
导引:要求多项式-4x2-6x+6的值,求出x的值或-
4x2-6x的值即可.而x的值目前我们无法求出,
所以我们需求出-4x2-6x的值.
解:因为2x2+3x=5,
所以-4x2-6x=-10(等式两边同时乘-2),
所以-4x2-6x+6=-4(等式两边同时加6).
总
结
知3-讲
利用等式的性质可以将等式作很多变形,求
某个多项式的值时,可以巧借等式的性质将已知
的条件进行变形,使之与要求的多项式相同.
知3-练
在横线上填上适当的数或式子:
(1)如果a+3=b-1,那么a+4=________;
(2)如果
x=3,那么x=________.
1
利用等式的性质解下列方程并检验:
(1)x-5=6;
(2)5x+4=0.
2
b
12
(1)11;
(2)
.
等式的性质
1.
等式两边加(或减)
同一个数(或式子),
结果仍相等
如果
a=b
那么a
±
c=b
±
c
2.
等式两边乘同一个数
或除以同一个不为0的
数,结果仍相等.
如果
a=b
那么
ac
=
bc
如果
a=b
那么
必做:
完成教材P83练习(2)(4),
P83习题3.1T4,T11
第三章
一元一次方程
3.1
从算式到方程
第2课时
等式的性质
1
课堂讲解
等式的性质1
等式的性质2
用等式的性质解方程
2
课时流程
逐点
导讲练
课堂小结
课后作业
复习提问
引出问题
(1)什么叫做方程?
(2)什么叫做一元一次方程?
(3)一元一次方程有哪几个特征?
①只含有一个未知数;
②未知数的次数都是1;
③整式方程.
(4)请你举出一个一元一次方程的例子.
1
知识点
等式的性质1
知1-导
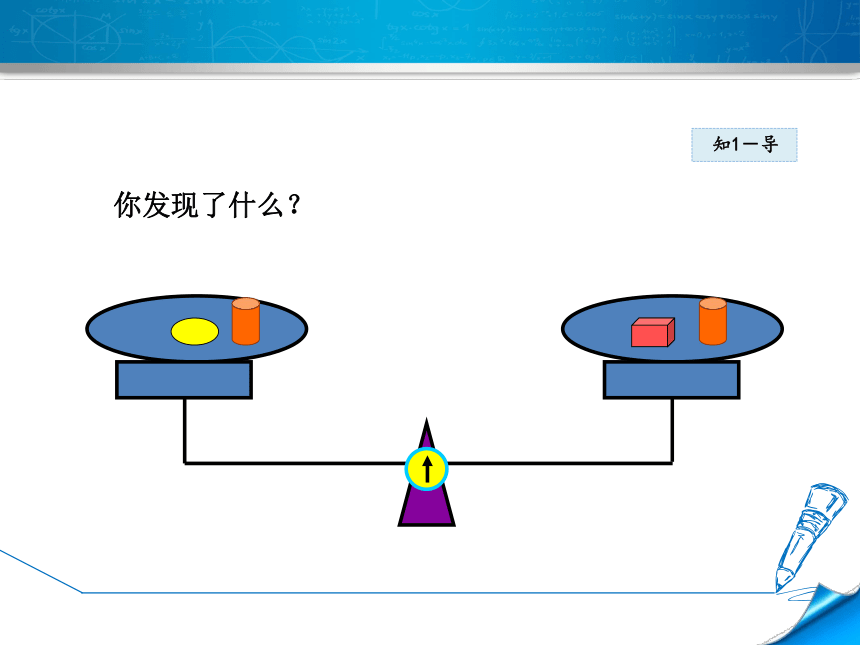
你发现了什么?
知1-导
你发现了什么?
知1-导
归
纳
(来自教材)
我们可以发现,如果在平衡的天平的两边都
加(或减)同样的量,天平还保持平衡.
知1-讲
等式的性质1:
等式两边加(或减)同一个数(或式子),结果仍相等,
用公式表示:如果a=b,那么a±c=b±c;
这里的a,b,c可以是具体的一个数,也可以是一
个代数式.
知1-讲
例1
根据等式的性质填空,并在后面的括号内填
上变形的根据.
(1)如果4x=x-2,那么4x-____=-2(
);
(2)如果2x+9=1,那么2x=1-____(
);
x
9
等式的性质1
等式的性质1
导引:(1)中方程的右边由x-2到-2,减了x,所以左边也
要减x;(2)中方程的左边由2x+9到2x,减了9,所
以右边也要减9.
知1-练
等式两边都加上(或__________)同一个__________(或________),结果仍相等;用字母表示:如果a=b,那么a±c=________.
1
若m+2n=p+2n,则m=________.依据是等式的性质________,它是将等式的两边______________.
2
减
数
式子
b±c
p
1
同时减去2n
知1-练
下列各种变形中,不正确的是( )
A.由2+x=5可得到x=5-2
B.由3x=2x-1可得到3x-2x=-1
C.由5x=4x+1可得到4x-5x=1
D.由6x-2x=-3可得到6x=2x-3
3
C
2
知识点
等式的性质2
知2-导
×3
÷
3
如:2=2
那么2×
3=2×3
如:6=6
那么6÷2=6÷2
知2-讲
等式的性质2:等式两边乘同一个数,或除以同一个
不为0的数,结果仍相等,用公式表示:如果a=b,
那么ac=bc,
(c≠0).
等式的性质2中,除以的同一个数不能为0.
知2-讲
例2
根据等式的性质填空,并在后面的括号内填
上变形的根据.
(1)如果-
=
,那么x=____(
);
(2)如果0.4a=3b,那么a=____(
).
等式的性质2
等式的性质2
导引:
(1)中方程的左边由-
到x,乘了-3,所以右边
也要乘-3;(2)中方程的左边由0.4a到a除以了0.4,
所以右边也要除以0.4,即乘
.
知2-练
等式2x-y=10变形为-4x+2y=-20的依据
为(
)
A.等式基本性质1
B.等式基本性质2
C.分数的基本性质
D.乘法分配律
1
B
知2-练
下列变形,正确的是(
)
A.如果a=b,那么
B.如果
,那么a=b
C.如果a2=3a,那么a=3
D.如果
-1=x,那么2x+1-1=3x
2
B
知2-练
已知x=y,下列各式:3x=3y,-2x=-2y,
=1,其中正确的有( )
A.1个
B.2个
C.3个
D.4个
3
C
知3-讲
3
知识点
用等式的性质解方程
例3
利用等式的性质解下列方程:
(1)
x+7
=
26;
(2)
-5x=20;
(3)
-5=4.
分析:要使方程x+7
=
26转化为x=a
(常数)的形式,
需去掉方程左边
的7,利用等式的性质1,方程
两边减7就得出x的值.你可以类似地考虑另两
个方程如何转化为x=a的形式.
知3-讲
解:(1)两边减7,得x+7-7=26-7.
于是x=19.
(2)两边除以-5,得
?
于是x=
-
4.
(3)两边加5,得
?
解以x为未知数的方程,就是把方程逐步转化为x=
a
(常
数)的形式,等式的性质是转化的重要依据.
(来自教材)
知3-讲
例4
若x=1是关于x的方程ax+b=c的解,求:
(1)(a+b-c)2的值;(2)
的值;
(3)|c-a-b-1|的值.
解:因为x=1是关于x的方程ax+b=c的解,
所以a+b=c.
(1)(a+b-c)2=[(a+b)-c]2=(c-c)2=0.
(2)
(3)|c-a-b-1|=|c-(a+b)-1|=|c-c-1|=1.
总
结
知3-讲
本例中a,b,c的值无法求出,表面上看似无
法求出相关式子的值,而运用整体思想就能达到求
解的目的.
知3-讲
例5
已知2x2+3x=5,求多项式-4x2-6x+6的值.
导引:要求多项式-4x2-6x+6的值,求出x的值或-
4x2-6x的值即可.而x的值目前我们无法求出,
所以我们需求出-4x2-6x的值.
解:因为2x2+3x=5,
所以-4x2-6x=-10(等式两边同时乘-2),
所以-4x2-6x+6=-4(等式两边同时加6).
总
结
知3-讲
利用等式的性质可以将等式作很多变形,求
某个多项式的值时,可以巧借等式的性质将已知
的条件进行变形,使之与要求的多项式相同.
知3-练
在横线上填上适当的数或式子:
(1)如果a+3=b-1,那么a+4=________;
(2)如果
x=3,那么x=________.
1
利用等式的性质解下列方程并检验:
(1)x-5=6;
(2)5x+4=0.
2
b
12
(1)11;
(2)
.
等式的性质
1.
等式两边加(或减)
同一个数(或式子),
结果仍相等
如果
a=b
那么a
±
c=b
±
c
2.
等式两边乘同一个数
或除以同一个不为0的
数,结果仍相等.
如果
a=b
那么
ac
=
bc
如果
a=b
那么
必做:
完成教材P83练习(2)(4),
P83习题3.1T4,T11
