人教版七上数学3.2.2 用移项法解一元一次方程课件(共26张)
文档属性
| 名称 | 人教版七上数学3.2.2 用移项法解一元一次方程课件(共26张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 22:23:31 | ||
图片预览







文档简介
(共26张PPT)
第三章
一元一次方程
3.2
解一元一次方程(一)——合并同类项与移项
第2课时
用移项法解一元
一次方程
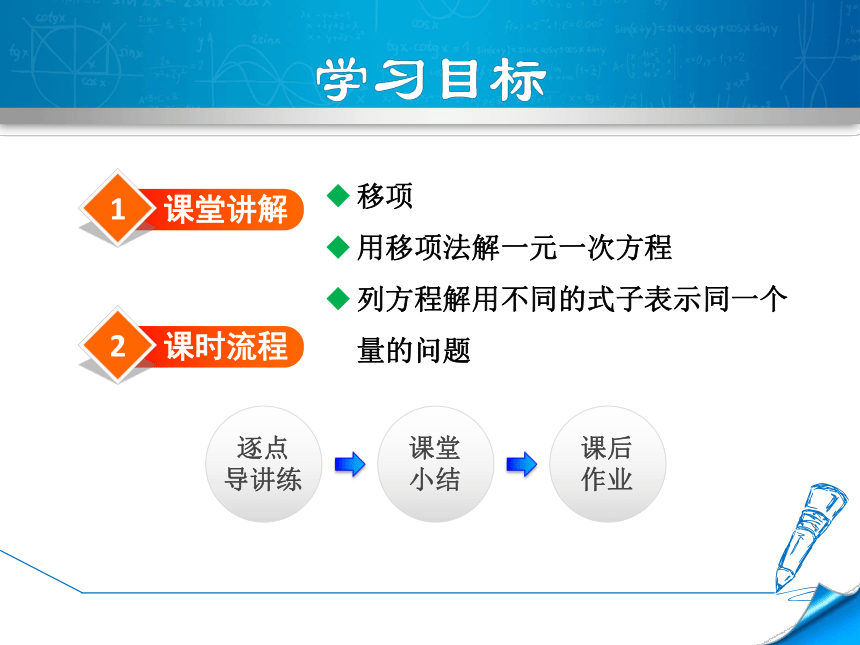
1
课堂讲解
移项
用移项法解一元一次方程
列方程解用不同的式子表示同一个量的问题
2
课时流程
逐点
导讲练
课堂小结
课后作业
等式两边都加上(或减去)同一个代数式,所得结果
仍是等式.
等式的基本性质2:
等式两边都乘以(或除以)同一个不等于0的数,所
得结果仍是等式.
等式的基本性质1:
1
知识点
移
项
知1-讲
6x
–
2
=
10
6x
=
10+
2
①
②
?式到?式有些什么变化?
“把原方程中的–
2
改变符号后,从方程的一边移到另一边,这种变形
叫
移项
.”
知1-讲
1.定义:把等式一边的某项变号后移到另一边叫
做移项.
2.方法:把方程右边含有未知数的项改变符号后
移到方程左边,把方程左边不含未知数的项改
变符号后移到方程右边,即“常数右边凑热闹,
未知左边来报到”.
知1-讲
例1
将方程5x+1=2x-3移项后,可得( )
A.5x-2x=-3+1
B.5x-2x=-3-1
C.5x+2x=-3-1
D.5x+2x=1-3
导引:A.常数项1移项时没有变号;C.2x移项时
没有变号;D.2x和常数项1移项时均未变
号,故选B.
B
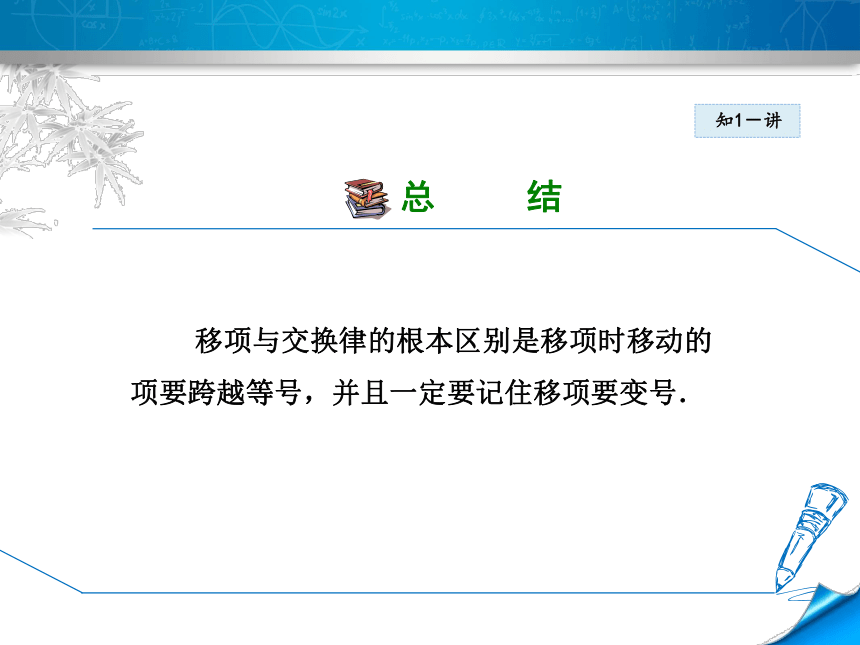
总
结
知1-讲
移项与交换律的根本区别是移项时移动的
项要跨越等号,并且一定要记住移项要变号.
知1-练
把方程3y-6=y+8变形为3y-y=8+6,这种变形叫做________,依据是__________________.
解方程时,移项法则的依据是( )
A.加法交换律
B.加法结合律
C.等式的性质1
D.等式的性质2
1
2
移项
等式的性质1
C
知1-练
解下列方程时,既要移含未知数的项,又要移常数项的是( )
A.2x=6-3x B.2x-4=3x+1
C.2x-2-x=1
D.x-5=7
3
B
知1-练
下列各式中的变形,属于移项的是( )
A.由3x-2y-1得-1-2y+3x
B.由9x-3=x+5得9x-3=5+x
C.由4-x=5x-2得5x-2=4-x
D.由2-x=x-2得2+2=x+x
4
D
2
知识点
用移项法解一元一次方程
知2-导
下面的框图表示了解这个方程的流程.
3x+20=4x-25
3x
-4x=
-25-20
-
x=
-45
x=45
移项
系数化为1
合并同类项
由上可知,这个班有45名学生.
知2-导
归
纳
移项解一元一次方程一般步骤:
①移项
②合并同类项
③系数化为1
知2-讲
(来自教材)
例2
解下列方程:
解:
(1)移项,得3x+2x=32
-7.
合并同类项,得5x=25.
系数化为1,得x=5.
(2)移项,得
合并同类项,得
系数化为1,得x=
-
8.
总
结
知2-讲
移项法是解简易方程的最基本的方法,其
目的是便于合并同类项,要把移项与多项式项的
移动区别开来;解题的关键是要记住“移项要变
号”这一要诀;其步骤为“一移二并三化”.
方程3x-4=3-2x的解答过程的正确顺序是( )
①合并同类项,得5x=7;
②移项,得3x+2x=3+4;
③系数化为1,得x=
.
A.①②③
B.③②①
C.②①③
D.③①②
知2-练
(来自教材)
解下列方程:
1
2
(1)1;
(2)-24.
C
知2-练
关于x的方程4x-6=3m与x-1=2有相同的解,则m等于( )
A.-2
B.2
C.-3
D.3
3
B
知2-讲
例3
已知|3x-6|+(2y-8)2=0,求2x-y的值.
解:
由题意,得|3x-6|=0,(2y-8)2=0.
所以3x-6=0,2y-8=0.
解得x=2,y=4.
所以2x-y=2×2-4=0.
知2-讲
例4
单项式7x2m-1yn+2与-9x3y-n+4的和仍是
单项式,求m-n的值.
解:由题意,得2m-1=3,n+2=-n+4,
解得m=2,n=1.
则m-n=2-1=1.
知2-练
1
若-2x2m+1y6与
x3m-1y10+4n是同类项,则m,n的值分别为( )
A.2,-1
B.-2,1
C.-1,2
D.-2,-1
A
知2-练
若“☆”是新规定的某种运算符号,x☆y=xy+x+y,则2☆m=-16中,m的值为( )
A.8
B.-8
C.6
D.-6
2
D
知3-讲
例5
某制药厂制造一批药品,如用旧工艺,则废水
排量要比环保限制的最大量还多200
t;如用新
工艺,则废水排量比环保限制的最大量少100
t
新、旧工艺的废水排量之比为2:
5,两种工艺的
废水排量各是多少?
分析:因为新、旧工艺的废水排量之比为2:
5,所以可
设它们分别为2xt和5xt,再根据它们与环保限
制的最大量之间的关系列方程.
3
知识点
列方程解用不同的式子表示同一个量的问题
知3-讲
(来自教材)
解:设新、旧工艺的废水排量分别为2xt
和5xt
.
根据废水排量与环保限制最大量之间的关系,得
5x-200=2x+100.
移项,得5x-2x=100+200.
合并同类项,得3x=300
.
系数化为1,得x=
100.
所以2x=200,5x=500.
答:新、旧工艺产生的废水排量分别为200
t和500
t.
等号两边代表哪个数量?
总
结
知3-讲
解决比例问题,一般设每份为未知数,用含
未知数的式子表示相关的量,再根据等量关系列出
方程.
知3-练
(来自教材)
王芳和李丽同时采摘櫻桃,王芳平均每小时采摘8
kg,李丽平均每小时采摘
7
kg.采摘结束后王芳从她采摘的樱桃中取出0.25
kg给了李丽,这时两人的
樱桃一样多.她们采摘用了多少时间?
1
设采摘了xh.
8x-0.25=7x+0.25,
x=0.5.
用移项法解一元一次方程的一般步骤:
移项→合并同类项→系数化为1.
移项的原则:
未知项左边来报到,常数项右边凑热闹.
移项的方法:
把方程中的某些项改变符号后,从方程的一边移到另
一边,即移项要变号.
必做:
完成教材P91习题3.2T2,T3(3)(4),
T8-T11
第三章
一元一次方程
3.2
解一元一次方程(一)——合并同类项与移项
第2课时
用移项法解一元
一次方程
1
课堂讲解
移项
用移项法解一元一次方程
列方程解用不同的式子表示同一个量的问题
2
课时流程
逐点
导讲练
课堂小结
课后作业
等式两边都加上(或减去)同一个代数式,所得结果
仍是等式.
等式的基本性质2:
等式两边都乘以(或除以)同一个不等于0的数,所
得结果仍是等式.
等式的基本性质1:
1
知识点
移
项
知1-讲
6x
–
2
=
10
6x
=
10+
2
①
②
?式到?式有些什么变化?
“把原方程中的–
2
改变符号后,从方程的一边移到另一边,这种变形
叫
移项
.”
知1-讲
1.定义:把等式一边的某项变号后移到另一边叫
做移项.
2.方法:把方程右边含有未知数的项改变符号后
移到方程左边,把方程左边不含未知数的项改
变符号后移到方程右边,即“常数右边凑热闹,
未知左边来报到”.
知1-讲
例1
将方程5x+1=2x-3移项后,可得( )
A.5x-2x=-3+1
B.5x-2x=-3-1
C.5x+2x=-3-1
D.5x+2x=1-3
导引:A.常数项1移项时没有变号;C.2x移项时
没有变号;D.2x和常数项1移项时均未变
号,故选B.
B
总
结
知1-讲
移项与交换律的根本区别是移项时移动的
项要跨越等号,并且一定要记住移项要变号.
知1-练
把方程3y-6=y+8变形为3y-y=8+6,这种变形叫做________,依据是__________________.
解方程时,移项法则的依据是( )
A.加法交换律
B.加法结合律
C.等式的性质1
D.等式的性质2
1
2
移项
等式的性质1
C
知1-练
解下列方程时,既要移含未知数的项,又要移常数项的是( )
A.2x=6-3x B.2x-4=3x+1
C.2x-2-x=1
D.x-5=7
3
B
知1-练
下列各式中的变形,属于移项的是( )
A.由3x-2y-1得-1-2y+3x
B.由9x-3=x+5得9x-3=5+x
C.由4-x=5x-2得5x-2=4-x
D.由2-x=x-2得2+2=x+x
4
D
2
知识点
用移项法解一元一次方程
知2-导
下面的框图表示了解这个方程的流程.
3x+20=4x-25
3x
-4x=
-25-20
-
x=
-45
x=45
移项
系数化为1
合并同类项
由上可知,这个班有45名学生.
知2-导
归
纳
移项解一元一次方程一般步骤:
①移项
②合并同类项
③系数化为1
知2-讲
(来自教材)
例2
解下列方程:
解:
(1)移项,得3x+2x=32
-7.
合并同类项,得5x=25.
系数化为1,得x=5.
(2)移项,得
合并同类项,得
系数化为1,得x=
-
8.
总
结
知2-讲
移项法是解简易方程的最基本的方法,其
目的是便于合并同类项,要把移项与多项式项的
移动区别开来;解题的关键是要记住“移项要变
号”这一要诀;其步骤为“一移二并三化”.
方程3x-4=3-2x的解答过程的正确顺序是( )
①合并同类项,得5x=7;
②移项,得3x+2x=3+4;
③系数化为1,得x=
.
A.①②③
B.③②①
C.②①③
D.③①②
知2-练
(来自教材)
解下列方程:
1
2
(1)1;
(2)-24.
C
知2-练
关于x的方程4x-6=3m与x-1=2有相同的解,则m等于( )
A.-2
B.2
C.-3
D.3
3
B
知2-讲
例3
已知|3x-6|+(2y-8)2=0,求2x-y的值.
解:
由题意,得|3x-6|=0,(2y-8)2=0.
所以3x-6=0,2y-8=0.
解得x=2,y=4.
所以2x-y=2×2-4=0.
知2-讲
例4
单项式7x2m-1yn+2与-9x3y-n+4的和仍是
单项式,求m-n的值.
解:由题意,得2m-1=3,n+2=-n+4,
解得m=2,n=1.
则m-n=2-1=1.
知2-练
1
若-2x2m+1y6与
x3m-1y10+4n是同类项,则m,n的值分别为( )
A.2,-1
B.-2,1
C.-1,2
D.-2,-1
A
知2-练
若“☆”是新规定的某种运算符号,x☆y=xy+x+y,则2☆m=-16中,m的值为( )
A.8
B.-8
C.6
D.-6
2
D
知3-讲
例5
某制药厂制造一批药品,如用旧工艺,则废水
排量要比环保限制的最大量还多200
t;如用新
工艺,则废水排量比环保限制的最大量少100
t
新、旧工艺的废水排量之比为2:
5,两种工艺的
废水排量各是多少?
分析:因为新、旧工艺的废水排量之比为2:
5,所以可
设它们分别为2xt和5xt,再根据它们与环保限
制的最大量之间的关系列方程.
3
知识点
列方程解用不同的式子表示同一个量的问题
知3-讲
(来自教材)
解:设新、旧工艺的废水排量分别为2xt
和5xt
.
根据废水排量与环保限制最大量之间的关系,得
5x-200=2x+100.
移项,得5x-2x=100+200.
合并同类项,得3x=300
.
系数化为1,得x=
100.
所以2x=200,5x=500.
答:新、旧工艺产生的废水排量分别为200
t和500
t.
等号两边代表哪个数量?
总
结
知3-讲
解决比例问题,一般设每份为未知数,用含
未知数的式子表示相关的量,再根据等量关系列出
方程.
知3-练
(来自教材)
王芳和李丽同时采摘櫻桃,王芳平均每小时采摘8
kg,李丽平均每小时采摘
7
kg.采摘结束后王芳从她采摘的樱桃中取出0.25
kg给了李丽,这时两人的
樱桃一样多.她们采摘用了多少时间?
1
设采摘了xh.
8x-0.25=7x+0.25,
x=0.5.
用移项法解一元一次方程的一般步骤:
移项→合并同类项→系数化为1.
移项的原则:
未知项左边来报到,常数项右边凑热闹.
移项的方法:
把方程中的某些项改变符号后,从方程的一边移到另
一边,即移项要变号.
必做:
完成教材P91习题3.2T2,T3(3)(4),
T8-T11
