2 2直线与圆的位置关系(备课件)【17张】-2021-2022学年高二数学同步备课系列(苏教版2019选择性必修第一册)
文档属性
| 名称 | 2 2直线与圆的位置关系(备课件)【17张】-2021-2022学年高二数学同步备课系列(苏教版2019选择性必修第一册) |

|
|
| 格式 | pptx | ||
| 文件大小 | 256.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 10:00:35 | ||
图片预览






文档简介
(共17张PPT)
2.2直线与圆的位置关系
学习目标
1.理解直线与圆的位置的种类;
2.能通过方程组的解和点到直线的距离公式判断直线与圆的位置关系.能够解决直线和圆相关的问题.
3.通过观察图形,理解并掌握直线与圆的位置关系,培养学生数形结合的思想.
复习引入
点M(x0,y0)与圆C:(x-a)2+(y-b)2=r2的位置关系及判断方法有几种?
C
M
复习引入
点M(x0,y0)与圆C:(x-a)2+(y-b)2=r2的位置关系及判断方法有几种?
位置关系 利用距离判断 利用方程判断
点M在圆上 CM=r (x0-a)2+(y0-b)2 r2
点M在圆外 CM>r (x0-a)2+(y0-b)2 r2
点M在圆内 CM=
>
<
C
M
M
M
情景引入
一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西40km点O处,已知港口位于台风中心正北30km点B处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
轮船A
港口B
台风O
轮船A
港口B
台风O
轮船A
港口B
台风O
(1)受影响的范围是半径长为20km的圆形区域, 那么它是否会受到台风的影响?
(2)受影响的范围是半径长为24km的圆形区域, 那么它是否会受到台风的影响?
(3)受影响的范围是半径长为25km的圆形区域, 那么它是否会受到台风的影响?
复习引入
●O
●O
●O
相离
相交
相切
交点个数
距离d
dd=r
d>r
2
1
0
怎么判断他们之间的关系的?
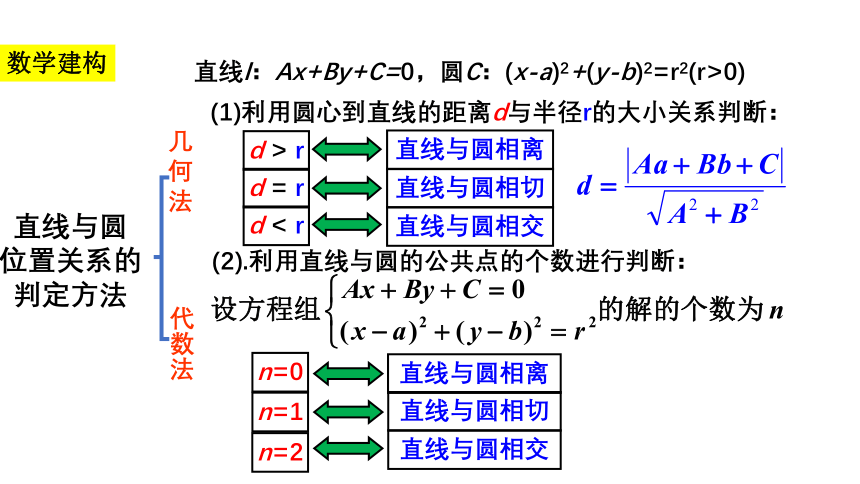
数学建构
(1)利用圆心到直线的距离d与半径r的大小关系判断:
直线与圆 位置关系的判定方法
d > r
d = r
d < r
直线与圆相离
直线与圆相切
直线与圆相交
(2).利用直线与圆的公共点的个数进行判断:
直线与圆相离
n=0
直线与圆相切
n=1
直线与圆相交
n=2
直线l:Ax+By+C=0,圆C:(x-a)2+(y-b)2=r2(r>0)
几何法
代数法
合作探究
例1.试判断下列直线和圆x2+y2=4的位置关系.
(1)2x-y+1= 0 (2)2x-y+5=0 (3)3x-4y+25=0
思考:再利用第二种方法时,需要求出其交点坐标吗?
数学建构
(1)利用圆心到直线的距离d与半径r的大小关系判断:
直线与圆的位置关系的判定方法
d > r
d = r
d < r
直线与圆相离
直线与圆相切
直线与圆相交
(2).利用直线与圆的公共点的个数进行判断:
直线与圆相离
n=0
△<0
直线与圆相切
n=1
△=0
直线与圆相交
n=2
△>0
直线l:Ax+By+C=0,圆C:(x-a)2+(y-b)2=r2(r>0)
几何法
代数法
数学应用
例1.试判断下列直线和圆x2+y2=4的位置关系.
(1)2x-y+1= 0 (2)2x-y+5=0 (3)3x-4y+25=0
思考:再利用第二种方法时,需要求出其交点坐标吗?
思考:这两种方法,哪一种更容易判断?
数学应用
变式.求直线 与圆
的交点坐标
所以,直线 l 与圆有两个交点,
它们的坐标分别是:
把 代入方程①,得
把 代入方程① ,得
A(2,0),B(1,3)
解:
数学应用
变式.已知直线 与圆
相交与A,B两点,求弦AB的长
所以,直线 l 与圆有两个交点,
它们的坐标分别是:
把 代入方程①,得
把 代入方程① ,得
A(2,0),B(1,3)
解:
数学建构
B
r
d
A(-2,4)
C(0,0)
概念辨析
解法一:
数学应用
解法二:
课堂小结
1.直线与圆位置关系判定方法
几何法
代数法
弦AB= ;
(其中d为圆心到弦的距离)
2.关于弦长、弦心距和半径之间的关系
切线PQ= ;
(其中Q为切点,d为点P到圆心的距离)
3.关于切线长、点心距和半径之间的关系
A
d
r
Q
r
d
P
达标测试
1.直线x-y-2=0被圆x2+y2=4所截得的弦长为 .
2.若过点(-2,1)作圆(x-3)2+(y-1)2=r2的切线有且只有一条,则r= .
5
3.若直线(m+1)x+y+1=0与圆(x-1)2+y2=1相切,则实数的m值为 .
-1
4.已知直线x-y+b=0与圆x2+y2=25相离,求b的取值范围.
谢谢!
2.2直线与圆的位置关系
学习目标
1.理解直线与圆的位置的种类;
2.能通过方程组的解和点到直线的距离公式判断直线与圆的位置关系.能够解决直线和圆相关的问题.
3.通过观察图形,理解并掌握直线与圆的位置关系,培养学生数形结合的思想.
复习引入
点M(x0,y0)与圆C:(x-a)2+(y-b)2=r2的位置关系及判断方法有几种?
C
M
复习引入
点M(x0,y0)与圆C:(x-a)2+(y-b)2=r2的位置关系及判断方法有几种?
位置关系 利用距离判断 利用方程判断
点M在圆上 CM=r (x0-a)2+(y0-b)2 r2
点M在圆外 CM>r (x0-a)2+(y0-b)2 r2
点M在圆内 CM
>
<
C
M
M
M
情景引入
一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西40km点O处,已知港口位于台风中心正北30km点B处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
轮船A
港口B
台风O
轮船A
港口B
台风O
轮船A
港口B
台风O
(1)受影响的范围是半径长为20km的圆形区域, 那么它是否会受到台风的影响?
(2)受影响的范围是半径长为24km的圆形区域, 那么它是否会受到台风的影响?
(3)受影响的范围是半径长为25km的圆形区域, 那么它是否会受到台风的影响?
复习引入
●O
●O
●O
相离
相交
相切
交点个数
距离d
d
d>r
2
1
0
怎么判断他们之间的关系的?
数学建构
(1)利用圆心到直线的距离d与半径r的大小关系判断:
直线与圆 位置关系的判定方法
d > r
d = r
d < r
直线与圆相离
直线与圆相切
直线与圆相交
(2).利用直线与圆的公共点的个数进行判断:
直线与圆相离
n=0
直线与圆相切
n=1
直线与圆相交
n=2
直线l:Ax+By+C=0,圆C:(x-a)2+(y-b)2=r2(r>0)
几何法
代数法
合作探究
例1.试判断下列直线和圆x2+y2=4的位置关系.
(1)2x-y+1= 0 (2)2x-y+5=0 (3)3x-4y+25=0
思考:再利用第二种方法时,需要求出其交点坐标吗?
数学建构
(1)利用圆心到直线的距离d与半径r的大小关系判断:
直线与圆的位置关系的判定方法
d > r
d = r
d < r
直线与圆相离
直线与圆相切
直线与圆相交
(2).利用直线与圆的公共点的个数进行判断:
直线与圆相离
n=0
△<0
直线与圆相切
n=1
△=0
直线与圆相交
n=2
△>0
直线l:Ax+By+C=0,圆C:(x-a)2+(y-b)2=r2(r>0)
几何法
代数法
数学应用
例1.试判断下列直线和圆x2+y2=4的位置关系.
(1)2x-y+1= 0 (2)2x-y+5=0 (3)3x-4y+25=0
思考:再利用第二种方法时,需要求出其交点坐标吗?
思考:这两种方法,哪一种更容易判断?
数学应用
变式.求直线 与圆
的交点坐标
所以,直线 l 与圆有两个交点,
它们的坐标分别是:
把 代入方程①,得
把 代入方程① ,得
A(2,0),B(1,3)
解:
数学应用
变式.已知直线 与圆
相交与A,B两点,求弦AB的长
所以,直线 l 与圆有两个交点,
它们的坐标分别是:
把 代入方程①,得
把 代入方程① ,得
A(2,0),B(1,3)
解:
数学建构
B
r
d
A(-2,4)
C(0,0)
概念辨析
解法一:
数学应用
解法二:
课堂小结
1.直线与圆位置关系判定方法
几何法
代数法
弦AB= ;
(其中d为圆心到弦的距离)
2.关于弦长、弦心距和半径之间的关系
切线PQ= ;
(其中Q为切点,d为点P到圆心的距离)
3.关于切线长、点心距和半径之间的关系
A
d
r
Q
r
d
P
达标测试
1.直线x-y-2=0被圆x2+y2=4所截得的弦长为 .
2.若过点(-2,1)作圆(x-3)2+(y-1)2=r2的切线有且只有一条,则r= .
5
3.若直线(m+1)x+y+1=0与圆(x-1)2+y2=1相切,则实数的m值为 .
-1
4.已知直线x-y+b=0与圆x2+y2=25相离,求b的取值范围.
谢谢!
