14.1.4:整式的乘法 同步提高课时练习(含解析)
文档属性
| 名称 | 14.1.4:整式的乘法 同步提高课时练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 737.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 00:00:00 | ||
图片预览




文档简介
14.1.4:整式的乘法
一、单选题
1.计算3a?(2b)的结果是( )
A.3ab B.6a C.6ab D.5ab
2.下列运算正确的是( )
A.false B.false C.false D.false
3.计算下列各式,结果为false的是( )
A.false B.false C.false D.false
4.已知false求false的值为( )
A.false B.false C.false D.false
5.代数式false的结果中,二次项系数是( )
A.false B.false C.false D.false
6.当false时,代数式false的值为2021,则当false时,代数式false的值为( )
A.2020 B.-2020 C.2019 D.-2019
7.若false,则false的值是( )
A.4 B.3 C.2 D.1
8.(x17y+x14z)÷(-x7)2 等于( )
A.x3y+z B.-xy3+z C.-x17y+z D.xy+z
9.下列计算正确的是( )
A.false
B.false
C.false
D.false
10.计算false的结果是( )
A.8m5 B.-8m5 C.8m6 D.-4m4+12m5
11.已知A=﹣4x2,B是多项式,在计算B+A时,小马虎同学把B+A看成了B?A,结果得32x5﹣16x4,则B+A为( )
A.﹣8x3+4x2 B.﹣8x3+8x2 C.﹣8x3 D.8x3
12.下列各式计算正确的是( )
A.(x+2)(x-5)=x2-2x-3 B.(x+3)(x-false)=x2+x-1
C.(x-false)(x+false)=x2-falsex-false D.(3x+2)(2x-3)=6x2-5x+6
13.已知(x-2)(1-kx)的结果中不含有x的一次项,则k的值为( )
A.2 B.-2 C.false D.false
14.(x7y4+x7z )÷x7等于( )
A.y4+z B.-4x2y4+xz C.x2y4+x2z D.x2y4+z
15.(2a3b2-10a4c )÷ 2a3等于( )
A.a6b2c B.a5b2c C.b2-5ac D.b4c -a4c
16.下列运算正确的是( )
A.false B.false C.false D.false
17.已知am=6,an=3,则a2m﹣3n的值为( )
A.false B.false C.2 D.9
18.已知x1,x2,…,x2016均为正数,且满足M=(x1+x2+…+x2015)(x2+x3+…+x2016),N=(x1+x2+…+x2016)(x2+x3+…+x2015),则M,N的大小关系是( )
A.M>N B.M<N C.M=N D.M≥N
19.如图1的8张长为a,宽为b(a<b)的小长方形纸片,按如图2的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
A.b=5a B.b=4a C.b=3a D.b=a
二、填空题
20.计算:false的结果是_______________.
21.已知当x=1时,多项式2ax2+bx+1=4,那么当x=2时,多项式ax2+bx-5=______.
22.若长方形的长为a+3b,宽为a+b,则这个长方形的面积为_____.
23.如果false与false的乘积中不含x2项,则m=______________.
24.已知false,false,则代数式false的值为______.
25.已知false,那么false__________.
26.如图,是我国南宋数学家杨辉所著的《详解九章算术》一书中,用下图的三角形解释false(false为整数)的展开时的系数规律,(按false的次数由大到小的顺序),此规律称之为“杨辉三角”.请依据此规律,写出false展开式中含false项的系数是__________.
false
false
false
false
false
false
false
false
false
false
···
···
27.若代数式false,则代数式false__________.
28.如图,正方形卡片A类、B类和长方形卡片C类各若干张,如果要拼一个长为false,宽为false的长方形,则需要C类卡片__________张.
29.当x=3时,代数式px3+qx+1的值为2019,则当x=-3时,代数式px3+qx+1的值是_____.
30.已知单项式3x2y3与﹣5x2y2的积为mx4yn,那么m﹣n=_____.
31.若 (x+2)( x2+mx+4) 的展开式中不含有 x 的二次项,则 m 的值为_________.
32.我们规定一种运算:false false=ad﹣bc,例如false false=3×6﹣4×5=﹣2.按照这种运算规定,已知false false=0,则false____.
33.如图所示,长方形ABCD中放置两个边长都为4cm的正方形AEFG与正方形CHIJ,若如图阴影部分的面积之和记为S1,长方形ABCD的面积记为S2,已知:3S2-S1=96,则长方形ABCD的周长为__________.
34.(1)false,false________;false________.
(2)猜想:false________(其中false为正整数,且false).
(3)利用(2)猜想的结论计:false________.
三、解答题
35.先化简,再求值:[(x+2y)(x-2y)-(x-y)2]÷(-2y),其中x=-1,y=2.
36.先化简,再求值:
3(2x+1)+2(3-x),其中x=-1.
37.已知false与false的乘积中不含false和false项,求false的值.
38.观察下列各式:
false;
false;
false;
false;
false
false.
(1)根据上面各式的规律填空:
①false ;
②false(false为正整数)= ;
(2)利用(1)中①的结论求false的值;
(3)若false,求false的值.
39.已知多项式false的结果中不含false项和false项,求false和false的值.
40.一天,小明和小红玩纸片拼图游戏.发现利用图①中的三种材料各若干可以拼出一些图形来解释某些等式,比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.
(1)图③可以解释为等式: .
(2)图④中阴影部分的面积为 .观察图④请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 .
(3)如图⑤,小明利用7个长为b,宽为a的长方形拼成如图所示的大长方形;若AB=4,若长方形AGMB的面积与长方形EDHN的面积的差为S,试计算S的值(用含a,b的代数式表示)
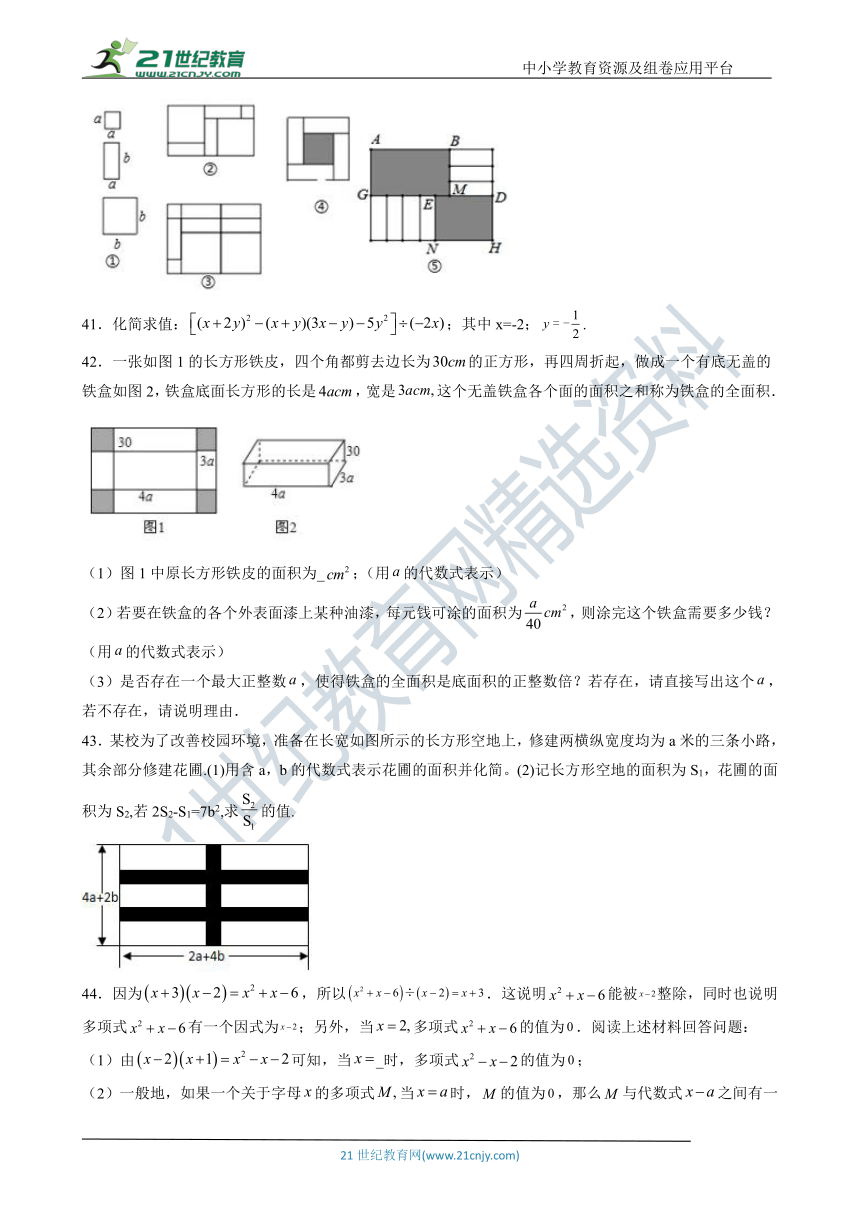
41.化简求值:false;其中x=-2;false.
42.一张如图1的长方形铁皮,四个角都剪去边长为false的正方形,再四周折起,做成一个有底无盖的铁盒如图2,铁盒底面长方形的长是false,宽是false这个无盖铁盒各个面的面积之和称为铁盒的全面积.
(1)图1中原长方形铁皮的面积为_false;(用false的代数式表示)
(2)若要在铁盒的各个外表面漆上某种油漆,每元钱可涂的面积为false,则涂完这个铁盒需要多少钱?(用false的代数式表示)
(3)是否存在一个最大正整数false,使得铁盒的全面积是底面积的正整数倍?若存在,请直接写出这个false,若不存在,请说明理由.
43.某校为了改善校园环境,准备在长宽如图所示的长方形空地上,修建两横纵宽度均为a米的三条小路,其余部分修建花圃.(1)用含a,b的代数式表示花圃的面积并化简。(2)记长方形空地的面积为S1,花圃的面积为S2,若2S2-S1=7b2,求false的值.
44.因为false,所以false.这说明false能被false整除,同时也说明多项式false有一个因式为false;另外,当false多项式false的值为false.阅读上述材料回答问题:
(1)由false可知,当false_时,多项式false的值为false;
(2)一般地,如果一个关于字母false的多项式false当false时,false的值为false,那么false与代数式false之间有一定的关系,这种关系是:_____;
(3)已知关于false的多项式false能被false整除,试求false的值.
45.李狗蛋同学在学习整式乘法公式这一节时,发现运用乘法公式在进行一些计算时特别简便,这激发了李狗蛋同学的学习兴趣,他想再探究一些有关整式乘法的公式,便主动查找资料进行学习,以下是他找来的资料题,请你一同跟李狗蛋同学探究一下:
(1)探究:false____;
false___;
false_____;
(2)猜想:false______(false为正整数,且false);
(3)利用上述猜想的结论计算:false的值.
参考答案
1.C
【解析】
根据单项式与单项式相乘,把他们的系数分别相乘,相同字母的幂分别相加,其余字母连同他的指数不变,作为积的因式,计算即可:3a?(2b)=3·2a?b=6ab.故选C.
2.D
【解析】分别根据合并同类项,只把系数相加减,字母与字母的次数不变;幂的乘方,底数不变指数相乘;同底数幂相除,底数不变指数相减,对各选项计算后利用排除法求解.
【解答】解:A、false,是整式加法,但不是同类项,不能合并,故本选项错误;
B、false,是整式加法,但不是同类项,不能合并,故本选项错误;
C、幂的乘方,底数不变指数相乘,故false,本选项错误;
D、同底数幂相除,底数不变指数相减,故false,本选项正确.
故选:D.
【点评】本题考查了整式的运算,熟练掌握运算性质是解题的关键.
3.D
【解析】分别计算每个选项然后进行判断即可.
【解答】解:A. false不能得到false,选项错误;
B. false,选项错误;
C. false,不能得到false,选项错误;
D. false,选项正确.
故选:D.
【点评】本题考查了同底数幂的运算,熟练掌握运算法则是解题的关键.
4.C
【解析】根据同底数幂除法的逆运算,幂的乘方的逆运算对false进行变形,再计算即可.
【解答】解:false=false=false=33÷23=false,
故选:C.
【点评】本题考查了同底数幂除法的逆运算,幂的乘方的逆运算,掌握运算法则是解题关键.
5.A
【解析】先根据多项式的乘法展开原式,再合并可得.
【解答】falsefalsefalse,
所以二次项系数是false.
故选:A.
【点评】本题主要考查了多项式乘以多项式的法则.注意不要漏项,漏字母,有同类项的合并同类项.
6.D
【解析】先将x=1代入代数式false中,得到p、q的关系式,再将x=-1代入即可解答.
【解答】将x=1代入代数式false中,得:false,
将x=-1代入代数式false中,得:
false=false,
故答案为:D.
【点评】本题考查的是代数式求值,会将所得关系式适当变形是解答的关键.
7.D
【解析】把所求代数式false变形为false,然后把条件整体代入求值即可.
【解答】∵false,
∴false
=false
=4×1-3
=1.
故选:D.
【点评】此题主要考查了代数式求值以及“整体代入”思想,解题的关键是把代数式false变形为false.
8.A
【解析】
(x17y+x14z)÷(-x7)2=(x17y+x14z)÷x14=x17y÷x14+x14z÷x14= x3y+z,
故选A.
9.D
【解析】根据合并同类项法则、单项式乘除法法则、积的乘方法则逐一进行计算即可得.
【解答】A.false,错误;
B、false,错误;
C、false,错误;
D、false,正确,
故选D.
【点评】本题考查了合并同类项、幂的乘方与积的乘方;单项式乘除法,熟练掌握各运算的运算法则是解题的关键.
10.A
【解析】根据积的乘方以及合并同类项进行计算即可.
【解答】原式=4m2?2m3
=8m5,
故选A.
【点评】本题考查了幂的乘方、积的乘方以及合并同类项的法则,掌握运算法则是解题的关键.
11.C
【解析】根据整式的运算法则即可求出答案.
【解答】由题意可知:-4x2?B=32x5-16x4,
∴B=-8x3+4x2
∴A+B=-8x3+4x2+(-4x2)=-8x3
故选C.
【点评】本题考查整式的运算,解题的关键是熟练运用整式的运算法则,本题属于基础题型.
12.C
【解析】
【解析】利用多项式乘多项式法则即可.
【解答】A. (x+2)(x-5)=x2-3x-10,不符合题意;
B. (x+3)(x-false)=x2+falsex-1,不符合题意;
C. (x-false)(x+false)=x2-falsex-false,符合题意;
D. (3x+2)(2x-3)=6x2-5 x-6,不符合题意,
故选C.
【点评】此题考查多项式乘多项式,解题关键在于掌握运算法则.
13.D
【解析】原式利用多项式乘以多项式法则计算,去括号合并后根据结果不含x的一次式,即可确定出k的值.
【解答】原式=x-kx2-2+2kx=-kx2+(2k+1)x-2,
由结果中不含x的一次式,得到2k+1=0,
解得:k=-false.
故选:D.
【点评】此题考查多项式乘以多项式,熟练掌握运算法则是解题的关键.
14.A
【解析】
(x7y4+x7z )÷x7=x7y4÷x7+x7z÷x7= y4+z,
故选A.
15.C
【解析】
(2a3b2-10a4c )÷ 2a3=2a3b2÷ 2a3-10a4c÷ 2a3= b2-5ac,
故选C.
16.B
【解析】
【解析】各项计算得到结果,即可作出判断.
【解答】解:A、原式=a4,不符合题意;
B、原式=false,符合题意;
C、原式=a5,不符合题意;
D、原式=a3b6,不符合题意,
故选B.
【点评】本题考查整式的混合运算,熟练掌握运算法则是解本题的关键.
17.A
【解析】原式利用同底数幂的除法法则及幂的乘方运算法则变形,将已知等式代入计算即可求出值.
【解答】∵am=6,an=3,
∴原式=(am)2÷(an)3=36÷27=false,
故选A.
【点评】本题考查了同底数幂的除法,以及幂的乘方与积的乘方,熟练掌握运算法则是解本题的关键.
18.A
【解析】设x1+x2+x3+…+x2015=A,对M,N变形后再作差M-N,结果与0比较大小,若大于0,则M>N;若等于0,则M=N;若小于0,则M【解答】解:令x2+x3+…+x2015=A,
则N=(x1+x2+x3+…+x2015+x2016)(x2+x3+…+x2015)
=(x1+A+x2016)?A
=x1?A+A2+x2016?A,
M=(x1+ x2+x3+…+x2015)(x2+x3+…+x2015+x2016)
=(A+x1)(A+x2016)
=A2+A?x2016+A?x1+x1?x2016,
∴M-N=(A2+A?x2016+A?x1+x1?x2016)-(x1?A+A2+x2016?A)
=x1?x2016,
∵x1,x2,…,x2016均为正数,
∴x1?x2016>0,
∴M>N,
故选:A.
【点评】本题主要考察整式的混合运算,通过对x2+x3+…+x2015=A进行换元,对整个式子化简后作差再与0比较大小,能想到换元法是解决本题的关键.
19.A
【解析】分别表示出左上角阴影部分的面积S1和右下角的阴影部分的面积S2,两者求差,根据当BC的长度变化时,按照同样的放置方式,S始终保持不变,即可求得a与b的数量关系.
【解答】解:设左上角阴影部分的面积为false,右下角的阴影部分的面积为false,
false
false
false
false.
false为定值,当false的长度变化时,按照同样的放置方式,false始终保持不变,
false,
false.
故选:false.
【点评】本题考查了整式的混合运算在几何图形问题中的应用,数形结合并根据题意正确表示出两部分阴影的面积之差是解题的关键.
20.false
【解析】利用单项式乘以单项式的运算法则进行计算,即可得到答案.
【解答】解:false,
故答案为:false.
【点评】本题考查了单项式乘以单项式,解题的关键是熟练掌握运算法则进行解题.
21.1
【解析】把x=1代入代数式2ax2+bx+1=4,可得2a+b+1=4,再将x=2与2a+b的值代入ax2+bx-5计算即可求出值.
【解答】解:把x=1代入2ax2+bx+1=4得:2a+b+1=4,即2a+b=3,
当x=2时,ax2+bx-5=4a+2b-5=2(2a+b)-5=6-5=1,
故答案为:1.
【点评】此题考查了代数式求值,熟练掌握运算法则是解本题的关键.
22.a2+4ab+3b2
【解析】根据长方形面积公式可得长方形的面积为(a+3b)(a+b),计算即可.
【解答】解:由题意得,长方形的面积:(a+3b)(a+b)=a2+4ab+3b2.
故答案为:a2+4ab+3b2.
【点评】本题考查长方形的面积公式和多项式乘法,熟练掌握多项式乘法计算法则是解题的关键.
23.false
【解析】先根据多项式的乘法法则展开,再根据题意,二次项的系数等于0列式求解即可.
【解答】解:(4x-2)(3x2+mx+1)=12x3+(4m-6)x2+(4-2m)x-2,
∵不含x2项,
∴4m-6=0,
解得m=false.
故答案为false.
【点评】此题考查多项式与多项式的乘法,运算法则需要熟练掌握,不含某一项就让这一项的系数等于0是解题的关键.
24.8
【解析】先计算false,再整体代入即可.
【解答】解:false.
故答案为:8
【点评】本题考查了多项式乘以多项式运算,熟知多项式乘以多项式法则是解题关键.
25.6
【解析】已知等式左边利用多项式乘以多项式法则计算,再利用多项式相等的条件求出a,b,c的值,代入原式计算即可求出值.
【解答】已知等式整理得:false,
可得false,false,false
则false,
故答案为false
【点评】此题考查了多项式乘多项式,熟练掌握运算法则是解本题的关键.
26.false
【解析】根据表格中的系数找出规律确定出所求即可.
【解答】解:依据此规律,写出(a+b)2019展开式中含a2018项的系数是2018+1=2019,
故答案为:2019
【点评】此题考查了整式乘法中的规律型:数字的变化类,找出系数的规律是解本题的关键.
27.false
【解析】将false变形为false的形式,然后将false整体代入可求得.
【解答】false=false
∵false
∴false=-5
故答案为:false
【点评】本题考查整体代入法,解题关键是将要求解的式子变形为条件已知的形式,整体代入求解.
28.7
【解析】根据长方形的面积=长×宽,求出长为a+3b,宽为2a+b的大长方形的面积是多少,判断出需要A类、B类、C类卡片各多少张即可.
【解答】解:∵(a+3b)(2a+b)=2a2+ab+6ab+3b2=2a2+7ab+3b2,
∴需要A类卡片2张、B类卡片3张、C类卡片7张,
故答案为:7.
【点评】此题主要考查了多项式乘多项式的运算方法,熟练掌握运算法则是解题的关键.
29.-2017
【解析】先把false代入,得false,然后把false代入代数式,得false,化简整理,即可得到答案.
【解答】解:∵当false时,有false,
∴false,
把false代入代数式,有
false;
故答案为:false.
【点评】本题考查代数式求值.根据已知条件,求不出p与q的具体值,必须把px3+qx当作一个整体,得出false与false时px3+qx的值是解决本题的关键.
30.﹣20.
【解析】将两单项式相乘后利用待定系数即可取出m与n的值.
【解答】解:3x2y3×(﹣5x2y2)=﹣15x4y5,
∴mx4yn=﹣15x4y5,
∴m=﹣15,n=5
∴m﹣n=﹣15﹣5=﹣20
故答案为﹣20
【点评】本题考查单项式乘以单项式,解题关键是熟练运用整式的乘法法则,本题属于基础题型.
31.m=-2.
【解析】
【解析】原式利用多项式乘以多项式法则计算,合并后根据结果不含x2项,求出m的值.
【解答】false,
由展开式中不含false项,得到m+2=0,
则m=?2.
故答案为?2.
【点评】本题主要考查多项式乘以多项式法则,熟悉掌握法则是关键.
32.false
【解析】利用题中的新定义化简已知等式得到一元一次方程,求出解即可.
【解答】由题意得:(x-2)(x+2)-(x+1)2=0,
化简得:-2x-5=0,
解得:x=false.
故答案为false.
【点评】本题主要考查了乘法公式的应用,根据新运算的定义得出方程是解决此题的关键.
33.24
【解析】设KF=a,FL=b,利用a,b表示出图中的阴影部分面积S1与长方形面积S2,然后根据3S2-S1=96可得a,b的关系式,然后可求周长.
【解答】设KF=a,FL=b,
由图可得,EK=BH=LJ=GD=4-a,KH=EB=GL=DJ==4-b,
∴S1=false
S2=false
∵3S2-S1=96
∴false
整理得:false
∴长方形ABCD的周长=false
故答案为:24.
【点评】本题考查列代数式表示图形面积以及代数式求值,利用长方形KFLI的长和宽表示出图形面积是解题的关键.
34.false false false false
【解析】(1)直接利用多项乘以多项式的运算法则,即可求出答案;
(2)利用(1)中的关系,找出规律,即可得到答案.
(3)利用(2)的结论,然后进行化简计算,即可得到答案.
【解答】解:(1)false
=false
=false;
false
=false
=false;
故答案为:false,false;
(2)∵false,
false,
false,
∴false;
故答案为:false;
(3)由(2)可知,
∵false,
∴false,
∴false
∴false
∴false;
故答案为:false.
【点评】本题考查了整式的数字变化规律,乘方的运算法则,以及平方差公式的知识,解题的关键是熟练掌握运算法则进行化简,从而正确的得到式子的规律.
35.6.
【解析】原式中括号中利用平方差公式,以及完全平方公式化简,再利用多项式除以单项式法则计算得到最简结果,把x与y的值代入计算即可求出值.
【解答】解:原式=[x2-4y2-x2-y2+2xy]÷(-2y)=falsey-x,
将x=-1,y=2代入得:原式=6.
【点评】此题考查了整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.
36.4x+9,5.
【解析】本题应对代数式去括号,合并同类项,从而将整式化为最简形式,然后把x的值代入即可.
【解答】原式=6x+3+6-2x
=4x+9,
当x=-1时,原式=5.
37.false,false.
【解析】先把false按多项式与多项式相乘的法则进行运算,再根据乘积不含false和false项,列出false,false,即可求解.
【解答】解:false
false
false
∵乘积中不含false和false项,
∴false,false,
∴false,false.
【点评】本题考查了多项式乘多项式,灵活掌握多项式乘以多项式的法则,注意各项符号的处理.
38.(1)①false;②false;(2)false;(3)1
【解析】(1)①根据上面各式的规律,可直接得到答案;
②根据上面各式的规律,可直接得到答案;
(2)根据(1)总结出的规律,可得:falsefalse,据此即可求出算式的值;
(3)根据(1)总结出的规律,可得:false=0,即可求解.
【解答】(1)①根据上面各式的规律,可得:
false;
②根据上面各式的规律,可得:
false;
(2)∵false,
∴false
false
false;
(3)∵false=0,
∴false,
∴false.
【点评】本题主要考查了多项式乘法中的规律性问题,有理数的混合运算的方法,要注意总结出规律,并能应用规律.
39.false,false
【解析】首先利用多项式乘法去括号,进而利用多项式(x2+px+q)(x2﹣3x+2)的结果中不含x3项和x2项,进而得出两项的系数为0,进而得出答案.
【解答】解:∵false
false
false
由多项式false的结果中不含false项和false项,
∴false,false,
解得:false,false.
故答案为:false,false.
【点评】此题主要考查了多项式乘法,正确利用多项式乘法去括号得出是解题关键.
40.(1)false;(2)false,false;(3)false.
【解析】(1)先求出大长方形的长、宽,再根据大长方形的面积等于四个正方形的面积与五个长方形的面积之和即可得;
(2)由图④可知,阴影部分为一个正方形,边长为false,根据正方形的面积公式即可得;根据大正方形的面积等于小正方形的面积与四个长方形的面积之和即可得;
(3)先根据长方形的面积公式求出长方形AGMB的面积、最大长方形的面积,再求出长方形EDHN的面积,两者作差即可得.
【解答】(1)由图可知,图③中大长方形的长为false,宽为false
则false
故答案为:false;
(2)由图④可知,图④是由四个长方形和中间一个小正方形组成一个大正方形
大正方形的边长为false,小正方形的边长为false
则阴影部分的面积为false
由大正方形的面积等于小正方形的面积与四个长方形的面积之和得:false,即false
故答案为:false,false;
(3)由图⑤可知,长方形AGMB的面积为false
最大长方形的面积为false
长方形EDHN的面积为false
则false
即false.
【点评】本题考查了整式的混合运算,理解题意,正确列出整式是解题关键.
41.x-y;false;
【解析】原式中括号中利用完全平方公式,以及多项式乘以多项式法则计算,去括号合并后利用多项式除以单项式法则计算得到最简结果,把x与y的值代入计算即可求出值.
【解答】false
=false
=false
=false
当 false,false 时,原式=false=false
【点评】此题考查了整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.
42.(1)12a2+420a+3600;(2)涂完这个铁盒需要(480a+16800)元;(3)a=35或7或5或1
【解析】(1)根据图形表示出原长方形铁皮的长和宽,进而表示出原长方形铁皮的面积即可;
(2)根据原长方形铁皮的面积剪去四个小正方形的面积,求出铁盒的表面积,乘以单价即可得到结果;
(3)假设存在,列出铁盒的全面积和底面积的公式,求整数倍数即可.
【解答】解:(1)原铁皮的面积是(4a+60)(3a+60)=12a2+420a+3600,
故答案为:12a2+420a+3600;
(2)油漆这个铁盒的表面积是:12a2+2×30×4a+2×30×3a=12a2+420a,
则油漆这个铁盒需要的钱数是:(12a2+420a)÷false=(12a2+420a)×false=480a+16800(元),
答:涂完这个铁盒需要(480a+16800)元;
(3)铁盒的全面积是4a×3a+4a×30×2+3a×30×2=12a2+420a,
底面积是4a×3a=12a2,
假设存在正整数n,使12a2+420a=n·12a2
整理得(n-1)a=35,
则a=35,n=2或a=7,n=6或a=5,n=8或a=1,n=36
所以存在铁盒的全面积是底面积的正整数倍,这时a=35或7或5或1.
【点评】此题考查整式的混合运算,正确掌握无盖铁盒的全面积与底面积的计算方法是解决问题的关键.
43.(1)2a2+10ab+8b2;(2)false.
【解析】(1)把三条小路使花圃的面积变为一个矩形的面积,所以花圃的面积=(4a+2b-2a)(2a+4b-a),然后利用展开公式展开合并即可;
(2)利用2S2-S1=7b2得到b=2a,则用a表示S1、S2,然后计算它们的比值.
【解答】解:(1)平移后图形为:(空白处为花圃的面积)
所以花圃的面积=(4a+2b-2a)(2a+4b-a)
=(2a+2b)(a+4b)
=2a2+8ab+2ab+8b2
=2a2+10ab+8b2;
(2)S1=(4a+2b)(2a+4b)=8a2+20ab+8b2,
S2=2a2+10ab+8b2;
∵2S2-S1=7b2,
∴2(2a2+10ab+8b2)-(8a2+20ab+8b2)=7b2,
∴b2=4a2,
∴b=2a,
∴S1=8a2+40a2+32a2=80a2,S2=2a2+20a2+32a2=54a2,
∴false.
【点评】本题考查了生活中的平移现象:在平面内,把一个图形整体沿某一的方向移动,这种图形的平行移动,叫做平移变换,简称平移.通过平移把不规则的图形变为规则图形.也考查了代数式.
44.(1)2或-1;(2)多项式M能被false整除;(3)k的值为3
【解析】(1)根据题意可知当因式false或false的值为0时,多项式false的值为0,由此可得答案;
(2)当false时,false的值为false,由此可判断false是多项式M的一个因式;
(3)根据题意可知false是多项式false的一个因式,结合(1)(2)两问可知当false时,false,由此可得k的值.
【解答】解:(1)∵false,
∴当false或false时,false,
即:当false或false时,false,
故答案为:2或-1;
(2)根据题意可知:false是多项式M的一个因式,
故答案为:多项式M能被false整除;
(3)根据题意可知:当false时,false,
即:当false时,false,
则false,
解得false,
答:k的值为3.
【点评】本题考查了整式的除法,是一道推理题,掌握好整式的除法法则是解题的关键.
45.(1)false,false,false;(2)false;(3)341
【解析】(1)根据平方差公式及多项式乘多项式法则计算即可;
(2)根据(1)的答案归纳总结即可;
(3)利用(2)的规律变形为(2)的形式计算即可.
【解答】解:(1)false,
false
false,
false
false,
故答案为:false,false,false;
(2)根据(1)的结果可知:falsefalse,
故答案为:false;
(3)原式false
falsefalse
false
false
false.
【点评】本题考查了平方差公式及多项式乘以多项式的变化规律,弄清题中的规律是解本题的关键.
一、单选题
1.计算3a?(2b)的结果是( )
A.3ab B.6a C.6ab D.5ab
2.下列运算正确的是( )
A.false B.false C.false D.false
3.计算下列各式,结果为false的是( )
A.false B.false C.false D.false
4.已知false求false的值为( )
A.false B.false C.false D.false
5.代数式false的结果中,二次项系数是( )
A.false B.false C.false D.false
6.当false时,代数式false的值为2021,则当false时,代数式false的值为( )
A.2020 B.-2020 C.2019 D.-2019
7.若false,则false的值是( )
A.4 B.3 C.2 D.1
8.(x17y+x14z)÷(-x7)2 等于( )
A.x3y+z B.-xy3+z C.-x17y+z D.xy+z
9.下列计算正确的是( )
A.false
B.false
C.false
D.false
10.计算false的结果是( )
A.8m5 B.-8m5 C.8m6 D.-4m4+12m5
11.已知A=﹣4x2,B是多项式,在计算B+A时,小马虎同学把B+A看成了B?A,结果得32x5﹣16x4,则B+A为( )
A.﹣8x3+4x2 B.﹣8x3+8x2 C.﹣8x3 D.8x3
12.下列各式计算正确的是( )
A.(x+2)(x-5)=x2-2x-3 B.(x+3)(x-false)=x2+x-1
C.(x-false)(x+false)=x2-falsex-false D.(3x+2)(2x-3)=6x2-5x+6
13.已知(x-2)(1-kx)的结果中不含有x的一次项,则k的值为( )
A.2 B.-2 C.false D.false
14.(x7y4+x7z )÷x7等于( )
A.y4+z B.-4x2y4+xz C.x2y4+x2z D.x2y4+z
15.(2a3b2-10a4c )÷ 2a3等于( )
A.a6b2c B.a5b2c C.b2-5ac D.b4c -a4c
16.下列运算正确的是( )
A.false B.false C.false D.false
17.已知am=6,an=3,则a2m﹣3n的值为( )
A.false B.false C.2 D.9
18.已知x1,x2,…,x2016均为正数,且满足M=(x1+x2+…+x2015)(x2+x3+…+x2016),N=(x1+x2+…+x2016)(x2+x3+…+x2015),则M,N的大小关系是( )
A.M>N B.M<N C.M=N D.M≥N
19.如图1的8张长为a,宽为b(a<b)的小长方形纸片,按如图2的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
A.b=5a B.b=4a C.b=3a D.b=a
二、填空题
20.计算:false的结果是_______________.
21.已知当x=1时,多项式2ax2+bx+1=4,那么当x=2时,多项式ax2+bx-5=______.
22.若长方形的长为a+3b,宽为a+b,则这个长方形的面积为_____.
23.如果false与false的乘积中不含x2项,则m=______________.
24.已知false,false,则代数式false的值为______.
25.已知false,那么false__________.
26.如图,是我国南宋数学家杨辉所著的《详解九章算术》一书中,用下图的三角形解释false(false为整数)的展开时的系数规律,(按false的次数由大到小的顺序),此规律称之为“杨辉三角”.请依据此规律,写出false展开式中含false项的系数是__________.
false
false
false
false
false
false
false
false
false
false
···
···
27.若代数式false,则代数式false__________.
28.如图,正方形卡片A类、B类和长方形卡片C类各若干张,如果要拼一个长为false,宽为false的长方形,则需要C类卡片__________张.
29.当x=3时,代数式px3+qx+1的值为2019,则当x=-3时,代数式px3+qx+1的值是_____.
30.已知单项式3x2y3与﹣5x2y2的积为mx4yn,那么m﹣n=_____.
31.若 (x+2)( x2+mx+4) 的展开式中不含有 x 的二次项,则 m 的值为_________.
32.我们规定一种运算:false false=ad﹣bc,例如false false=3×6﹣4×5=﹣2.按照这种运算规定,已知false false=0,则false____.
33.如图所示,长方形ABCD中放置两个边长都为4cm的正方形AEFG与正方形CHIJ,若如图阴影部分的面积之和记为S1,长方形ABCD的面积记为S2,已知:3S2-S1=96,则长方形ABCD的周长为__________.
34.(1)false,false________;false________.
(2)猜想:false________(其中false为正整数,且false).
(3)利用(2)猜想的结论计:false________.
三、解答题
35.先化简,再求值:[(x+2y)(x-2y)-(x-y)2]÷(-2y),其中x=-1,y=2.
36.先化简,再求值:
3(2x+1)+2(3-x),其中x=-1.
37.已知false与false的乘积中不含false和false项,求false的值.
38.观察下列各式:
false;
false;
false;
false;
false
false.
(1)根据上面各式的规律填空:
①false ;
②false(false为正整数)= ;
(2)利用(1)中①的结论求false的值;
(3)若false,求false的值.
39.已知多项式false的结果中不含false项和false项,求false和false的值.
40.一天,小明和小红玩纸片拼图游戏.发现利用图①中的三种材料各若干可以拼出一些图形来解释某些等式,比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.
(1)图③可以解释为等式: .
(2)图④中阴影部分的面积为 .观察图④请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 .
(3)如图⑤,小明利用7个长为b,宽为a的长方形拼成如图所示的大长方形;若AB=4,若长方形AGMB的面积与长方形EDHN的面积的差为S,试计算S的值(用含a,b的代数式表示)
41.化简求值:false;其中x=-2;false.
42.一张如图1的长方形铁皮,四个角都剪去边长为false的正方形,再四周折起,做成一个有底无盖的铁盒如图2,铁盒底面长方形的长是false,宽是false这个无盖铁盒各个面的面积之和称为铁盒的全面积.
(1)图1中原长方形铁皮的面积为_false;(用false的代数式表示)
(2)若要在铁盒的各个外表面漆上某种油漆,每元钱可涂的面积为false,则涂完这个铁盒需要多少钱?(用false的代数式表示)
(3)是否存在一个最大正整数false,使得铁盒的全面积是底面积的正整数倍?若存在,请直接写出这个false,若不存在,请说明理由.
43.某校为了改善校园环境,准备在长宽如图所示的长方形空地上,修建两横纵宽度均为a米的三条小路,其余部分修建花圃.(1)用含a,b的代数式表示花圃的面积并化简。(2)记长方形空地的面积为S1,花圃的面积为S2,若2S2-S1=7b2,求false的值.
44.因为false,所以false.这说明false能被false整除,同时也说明多项式false有一个因式为false;另外,当false多项式false的值为false.阅读上述材料回答问题:
(1)由false可知,当false_时,多项式false的值为false;
(2)一般地,如果一个关于字母false的多项式false当false时,false的值为false,那么false与代数式false之间有一定的关系,这种关系是:_____;
(3)已知关于false的多项式false能被false整除,试求false的值.
45.李狗蛋同学在学习整式乘法公式这一节时,发现运用乘法公式在进行一些计算时特别简便,这激发了李狗蛋同学的学习兴趣,他想再探究一些有关整式乘法的公式,便主动查找资料进行学习,以下是他找来的资料题,请你一同跟李狗蛋同学探究一下:
(1)探究:false____;
false___;
false_____;
(2)猜想:false______(false为正整数,且false);
(3)利用上述猜想的结论计算:false的值.
参考答案
1.C
【解析】
根据单项式与单项式相乘,把他们的系数分别相乘,相同字母的幂分别相加,其余字母连同他的指数不变,作为积的因式,计算即可:3a?(2b)=3·2a?b=6ab.故选C.
2.D
【解析】分别根据合并同类项,只把系数相加减,字母与字母的次数不变;幂的乘方,底数不变指数相乘;同底数幂相除,底数不变指数相减,对各选项计算后利用排除法求解.
【解答】解:A、false,是整式加法,但不是同类项,不能合并,故本选项错误;
B、false,是整式加法,但不是同类项,不能合并,故本选项错误;
C、幂的乘方,底数不变指数相乘,故false,本选项错误;
D、同底数幂相除,底数不变指数相减,故false,本选项正确.
故选:D.
【点评】本题考查了整式的运算,熟练掌握运算性质是解题的关键.
3.D
【解析】分别计算每个选项然后进行判断即可.
【解答】解:A. false不能得到false,选项错误;
B. false,选项错误;
C. false,不能得到false,选项错误;
D. false,选项正确.
故选:D.
【点评】本题考查了同底数幂的运算,熟练掌握运算法则是解题的关键.
4.C
【解析】根据同底数幂除法的逆运算,幂的乘方的逆运算对false进行变形,再计算即可.
【解答】解:false=false=false=33÷23=false,
故选:C.
【点评】本题考查了同底数幂除法的逆运算,幂的乘方的逆运算,掌握运算法则是解题关键.
5.A
【解析】先根据多项式的乘法展开原式,再合并可得.
【解答】falsefalsefalse,
所以二次项系数是false.
故选:A.
【点评】本题主要考查了多项式乘以多项式的法则.注意不要漏项,漏字母,有同类项的合并同类项.
6.D
【解析】先将x=1代入代数式false中,得到p、q的关系式,再将x=-1代入即可解答.
【解答】将x=1代入代数式false中,得:false,
将x=-1代入代数式false中,得:
false=false,
故答案为:D.
【点评】本题考查的是代数式求值,会将所得关系式适当变形是解答的关键.
7.D
【解析】把所求代数式false变形为false,然后把条件整体代入求值即可.
【解答】∵false,
∴false
=false
=4×1-3
=1.
故选:D.
【点评】此题主要考查了代数式求值以及“整体代入”思想,解题的关键是把代数式false变形为false.
8.A
【解析】
(x17y+x14z)÷(-x7)2=(x17y+x14z)÷x14=x17y÷x14+x14z÷x14= x3y+z,
故选A.
9.D
【解析】根据合并同类项法则、单项式乘除法法则、积的乘方法则逐一进行计算即可得.
【解答】A.false,错误;
B、false,错误;
C、false,错误;
D、false,正确,
故选D.
【点评】本题考查了合并同类项、幂的乘方与积的乘方;单项式乘除法,熟练掌握各运算的运算法则是解题的关键.
10.A
【解析】根据积的乘方以及合并同类项进行计算即可.
【解答】原式=4m2?2m3
=8m5,
故选A.
【点评】本题考查了幂的乘方、积的乘方以及合并同类项的法则,掌握运算法则是解题的关键.
11.C
【解析】根据整式的运算法则即可求出答案.
【解答】由题意可知:-4x2?B=32x5-16x4,
∴B=-8x3+4x2
∴A+B=-8x3+4x2+(-4x2)=-8x3
故选C.
【点评】本题考查整式的运算,解题的关键是熟练运用整式的运算法则,本题属于基础题型.
12.C
【解析】
【解析】利用多项式乘多项式法则即可.
【解答】A. (x+2)(x-5)=x2-3x-10,不符合题意;
B. (x+3)(x-false)=x2+falsex-1,不符合题意;
C. (x-false)(x+false)=x2-falsex-false,符合题意;
D. (3x+2)(2x-3)=6x2-5 x-6,不符合题意,
故选C.
【点评】此题考查多项式乘多项式,解题关键在于掌握运算法则.
13.D
【解析】原式利用多项式乘以多项式法则计算,去括号合并后根据结果不含x的一次式,即可确定出k的值.
【解答】原式=x-kx2-2+2kx=-kx2+(2k+1)x-2,
由结果中不含x的一次式,得到2k+1=0,
解得:k=-false.
故选:D.
【点评】此题考查多项式乘以多项式,熟练掌握运算法则是解题的关键.
14.A
【解析】
(x7y4+x7z )÷x7=x7y4÷x7+x7z÷x7= y4+z,
故选A.
15.C
【解析】
(2a3b2-10a4c )÷ 2a3=2a3b2÷ 2a3-10a4c÷ 2a3= b2-5ac,
故选C.
16.B
【解析】
【解析】各项计算得到结果,即可作出判断.
【解答】解:A、原式=a4,不符合题意;
B、原式=false,符合题意;
C、原式=a5,不符合题意;
D、原式=a3b6,不符合题意,
故选B.
【点评】本题考查整式的混合运算,熟练掌握运算法则是解本题的关键.
17.A
【解析】原式利用同底数幂的除法法则及幂的乘方运算法则变形,将已知等式代入计算即可求出值.
【解答】∵am=6,an=3,
∴原式=(am)2÷(an)3=36÷27=false,
故选A.
【点评】本题考查了同底数幂的除法,以及幂的乘方与积的乘方,熟练掌握运算法则是解本题的关键.
18.A
【解析】设x1+x2+x3+…+x2015=A,对M,N变形后再作差M-N,结果与0比较大小,若大于0,则M>N;若等于0,则M=N;若小于0,则M
则N=(x1+x2+x3+…+x2015+x2016)(x2+x3+…+x2015)
=(x1+A+x2016)?A
=x1?A+A2+x2016?A,
M=(x1+ x2+x3+…+x2015)(x2+x3+…+x2015+x2016)
=(A+x1)(A+x2016)
=A2+A?x2016+A?x1+x1?x2016,
∴M-N=(A2+A?x2016+A?x1+x1?x2016)-(x1?A+A2+x2016?A)
=x1?x2016,
∵x1,x2,…,x2016均为正数,
∴x1?x2016>0,
∴M>N,
故选:A.
【点评】本题主要考察整式的混合运算,通过对x2+x3+…+x2015=A进行换元,对整个式子化简后作差再与0比较大小,能想到换元法是解决本题的关键.
19.A
【解析】分别表示出左上角阴影部分的面积S1和右下角的阴影部分的面积S2,两者求差,根据当BC的长度变化时,按照同样的放置方式,S始终保持不变,即可求得a与b的数量关系.
【解答】解:设左上角阴影部分的面积为false,右下角的阴影部分的面积为false,
false
false
false
false.
false为定值,当false的长度变化时,按照同样的放置方式,false始终保持不变,
false,
false.
故选:false.
【点评】本题考查了整式的混合运算在几何图形问题中的应用,数形结合并根据题意正确表示出两部分阴影的面积之差是解题的关键.
20.false
【解析】利用单项式乘以单项式的运算法则进行计算,即可得到答案.
【解答】解:false,
故答案为:false.
【点评】本题考查了单项式乘以单项式,解题的关键是熟练掌握运算法则进行解题.
21.1
【解析】把x=1代入代数式2ax2+bx+1=4,可得2a+b+1=4,再将x=2与2a+b的值代入ax2+bx-5计算即可求出值.
【解答】解:把x=1代入2ax2+bx+1=4得:2a+b+1=4,即2a+b=3,
当x=2时,ax2+bx-5=4a+2b-5=2(2a+b)-5=6-5=1,
故答案为:1.
【点评】此题考查了代数式求值,熟练掌握运算法则是解本题的关键.
22.a2+4ab+3b2
【解析】根据长方形面积公式可得长方形的面积为(a+3b)(a+b),计算即可.
【解答】解:由题意得,长方形的面积:(a+3b)(a+b)=a2+4ab+3b2.
故答案为:a2+4ab+3b2.
【点评】本题考查长方形的面积公式和多项式乘法,熟练掌握多项式乘法计算法则是解题的关键.
23.false
【解析】先根据多项式的乘法法则展开,再根据题意,二次项的系数等于0列式求解即可.
【解答】解:(4x-2)(3x2+mx+1)=12x3+(4m-6)x2+(4-2m)x-2,
∵不含x2项,
∴4m-6=0,
解得m=false.
故答案为false.
【点评】此题考查多项式与多项式的乘法,运算法则需要熟练掌握,不含某一项就让这一项的系数等于0是解题的关键.
24.8
【解析】先计算false,再整体代入即可.
【解答】解:false.
故答案为:8
【点评】本题考查了多项式乘以多项式运算,熟知多项式乘以多项式法则是解题关键.
25.6
【解析】已知等式左边利用多项式乘以多项式法则计算,再利用多项式相等的条件求出a,b,c的值,代入原式计算即可求出值.
【解答】已知等式整理得:false,
可得false,false,false
则false,
故答案为false
【点评】此题考查了多项式乘多项式,熟练掌握运算法则是解本题的关键.
26.false
【解析】根据表格中的系数找出规律确定出所求即可.
【解答】解:依据此规律,写出(a+b)2019展开式中含a2018项的系数是2018+1=2019,
故答案为:2019
【点评】此题考查了整式乘法中的规律型:数字的变化类,找出系数的规律是解本题的关键.
27.false
【解析】将false变形为false的形式,然后将false整体代入可求得.
【解答】false=false
∵false
∴false=-5
故答案为:false
【点评】本题考查整体代入法,解题关键是将要求解的式子变形为条件已知的形式,整体代入求解.
28.7
【解析】根据长方形的面积=长×宽,求出长为a+3b,宽为2a+b的大长方形的面积是多少,判断出需要A类、B类、C类卡片各多少张即可.
【解答】解:∵(a+3b)(2a+b)=2a2+ab+6ab+3b2=2a2+7ab+3b2,
∴需要A类卡片2张、B类卡片3张、C类卡片7张,
故答案为:7.
【点评】此题主要考查了多项式乘多项式的运算方法,熟练掌握运算法则是解题的关键.
29.-2017
【解析】先把false代入,得false,然后把false代入代数式,得false,化简整理,即可得到答案.
【解答】解:∵当false时,有false,
∴false,
把false代入代数式,有
false;
故答案为:false.
【点评】本题考查代数式求值.根据已知条件,求不出p与q的具体值,必须把px3+qx当作一个整体,得出false与false时px3+qx的值是解决本题的关键.
30.﹣20.
【解析】将两单项式相乘后利用待定系数即可取出m与n的值.
【解答】解:3x2y3×(﹣5x2y2)=﹣15x4y5,
∴mx4yn=﹣15x4y5,
∴m=﹣15,n=5
∴m﹣n=﹣15﹣5=﹣20
故答案为﹣20
【点评】本题考查单项式乘以单项式,解题关键是熟练运用整式的乘法法则,本题属于基础题型.
31.m=-2.
【解析】
【解析】原式利用多项式乘以多项式法则计算,合并后根据结果不含x2项,求出m的值.
【解答】false,
由展开式中不含false项,得到m+2=0,
则m=?2.
故答案为?2.
【点评】本题主要考查多项式乘以多项式法则,熟悉掌握法则是关键.
32.false
【解析】利用题中的新定义化简已知等式得到一元一次方程,求出解即可.
【解答】由题意得:(x-2)(x+2)-(x+1)2=0,
化简得:-2x-5=0,
解得:x=false.
故答案为false.
【点评】本题主要考查了乘法公式的应用,根据新运算的定义得出方程是解决此题的关键.
33.24
【解析】设KF=a,FL=b,利用a,b表示出图中的阴影部分面积S1与长方形面积S2,然后根据3S2-S1=96可得a,b的关系式,然后可求周长.
【解答】设KF=a,FL=b,
由图可得,EK=BH=LJ=GD=4-a,KH=EB=GL=DJ==4-b,
∴S1=false
S2=false
∵3S2-S1=96
∴false
整理得:false
∴长方形ABCD的周长=false
故答案为:24.
【点评】本题考查列代数式表示图形面积以及代数式求值,利用长方形KFLI的长和宽表示出图形面积是解题的关键.
34.false false false false
【解析】(1)直接利用多项乘以多项式的运算法则,即可求出答案;
(2)利用(1)中的关系,找出规律,即可得到答案.
(3)利用(2)的结论,然后进行化简计算,即可得到答案.
【解答】解:(1)false
=false
=false;
false
=false
=false;
故答案为:false,false;
(2)∵false,
false,
false,
∴false;
故答案为:false;
(3)由(2)可知,
∵false,
∴false,
∴false
∴false
∴false;
故答案为:false.
【点评】本题考查了整式的数字变化规律,乘方的运算法则,以及平方差公式的知识,解题的关键是熟练掌握运算法则进行化简,从而正确的得到式子的规律.
35.6.
【解析】原式中括号中利用平方差公式,以及完全平方公式化简,再利用多项式除以单项式法则计算得到最简结果,把x与y的值代入计算即可求出值.
【解答】解:原式=[x2-4y2-x2-y2+2xy]÷(-2y)=falsey-x,
将x=-1,y=2代入得:原式=6.
【点评】此题考查了整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.
36.4x+9,5.
【解析】本题应对代数式去括号,合并同类项,从而将整式化为最简形式,然后把x的值代入即可.
【解答】原式=6x+3+6-2x
=4x+9,
当x=-1时,原式=5.
37.false,false.
【解析】先把false按多项式与多项式相乘的法则进行运算,再根据乘积不含false和false项,列出false,false,即可求解.
【解答】解:false
false
false
∵乘积中不含false和false项,
∴false,false,
∴false,false.
【点评】本题考查了多项式乘多项式,灵活掌握多项式乘以多项式的法则,注意各项符号的处理.
38.(1)①false;②false;(2)false;(3)1
【解析】(1)①根据上面各式的规律,可直接得到答案;
②根据上面各式的规律,可直接得到答案;
(2)根据(1)总结出的规律,可得:falsefalse,据此即可求出算式的值;
(3)根据(1)总结出的规律,可得:false=0,即可求解.
【解答】(1)①根据上面各式的规律,可得:
false;
②根据上面各式的规律,可得:
false;
(2)∵false,
∴false
false
false;
(3)∵false=0,
∴false,
∴false.
【点评】本题主要考查了多项式乘法中的规律性问题,有理数的混合运算的方法,要注意总结出规律,并能应用规律.
39.false,false
【解析】首先利用多项式乘法去括号,进而利用多项式(x2+px+q)(x2﹣3x+2)的结果中不含x3项和x2项,进而得出两项的系数为0,进而得出答案.
【解答】解:∵false
false
false
由多项式false的结果中不含false项和false项,
∴false,false,
解得:false,false.
故答案为:false,false.
【点评】此题主要考查了多项式乘法,正确利用多项式乘法去括号得出是解题关键.
40.(1)false;(2)false,false;(3)false.
【解析】(1)先求出大长方形的长、宽,再根据大长方形的面积等于四个正方形的面积与五个长方形的面积之和即可得;
(2)由图④可知,阴影部分为一个正方形,边长为false,根据正方形的面积公式即可得;根据大正方形的面积等于小正方形的面积与四个长方形的面积之和即可得;
(3)先根据长方形的面积公式求出长方形AGMB的面积、最大长方形的面积,再求出长方形EDHN的面积,两者作差即可得.
【解答】(1)由图可知,图③中大长方形的长为false,宽为false
则false
故答案为:false;
(2)由图④可知,图④是由四个长方形和中间一个小正方形组成一个大正方形
大正方形的边长为false,小正方形的边长为false
则阴影部分的面积为false
由大正方形的面积等于小正方形的面积与四个长方形的面积之和得:false,即false
故答案为:false,false;
(3)由图⑤可知,长方形AGMB的面积为false
最大长方形的面积为false
长方形EDHN的面积为false
则false
即false.
【点评】本题考查了整式的混合运算,理解题意,正确列出整式是解题关键.
41.x-y;false;
【解析】原式中括号中利用完全平方公式,以及多项式乘以多项式法则计算,去括号合并后利用多项式除以单项式法则计算得到最简结果,把x与y的值代入计算即可求出值.
【解答】false
=false
=false
=false
当 false,false 时,原式=false=false
【点评】此题考查了整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.
42.(1)12a2+420a+3600;(2)涂完这个铁盒需要(480a+16800)元;(3)a=35或7或5或1
【解析】(1)根据图形表示出原长方形铁皮的长和宽,进而表示出原长方形铁皮的面积即可;
(2)根据原长方形铁皮的面积剪去四个小正方形的面积,求出铁盒的表面积,乘以单价即可得到结果;
(3)假设存在,列出铁盒的全面积和底面积的公式,求整数倍数即可.
【解答】解:(1)原铁皮的面积是(4a+60)(3a+60)=12a2+420a+3600,
故答案为:12a2+420a+3600;
(2)油漆这个铁盒的表面积是:12a2+2×30×4a+2×30×3a=12a2+420a,
则油漆这个铁盒需要的钱数是:(12a2+420a)÷false=(12a2+420a)×false=480a+16800(元),
答:涂完这个铁盒需要(480a+16800)元;
(3)铁盒的全面积是4a×3a+4a×30×2+3a×30×2=12a2+420a,
底面积是4a×3a=12a2,
假设存在正整数n,使12a2+420a=n·12a2
整理得(n-1)a=35,
则a=35,n=2或a=7,n=6或a=5,n=8或a=1,n=36
所以存在铁盒的全面积是底面积的正整数倍,这时a=35或7或5或1.
【点评】此题考查整式的混合运算,正确掌握无盖铁盒的全面积与底面积的计算方法是解决问题的关键.
43.(1)2a2+10ab+8b2;(2)false.
【解析】(1)把三条小路使花圃的面积变为一个矩形的面积,所以花圃的面积=(4a+2b-2a)(2a+4b-a),然后利用展开公式展开合并即可;
(2)利用2S2-S1=7b2得到b=2a,则用a表示S1、S2,然后计算它们的比值.
【解答】解:(1)平移后图形为:(空白处为花圃的面积)
所以花圃的面积=(4a+2b-2a)(2a+4b-a)
=(2a+2b)(a+4b)
=2a2+8ab+2ab+8b2
=2a2+10ab+8b2;
(2)S1=(4a+2b)(2a+4b)=8a2+20ab+8b2,
S2=2a2+10ab+8b2;
∵2S2-S1=7b2,
∴2(2a2+10ab+8b2)-(8a2+20ab+8b2)=7b2,
∴b2=4a2,
∴b=2a,
∴S1=8a2+40a2+32a2=80a2,S2=2a2+20a2+32a2=54a2,
∴false.
【点评】本题考查了生活中的平移现象:在平面内,把一个图形整体沿某一的方向移动,这种图形的平行移动,叫做平移变换,简称平移.通过平移把不规则的图形变为规则图形.也考查了代数式.
44.(1)2或-1;(2)多项式M能被false整除;(3)k的值为3
【解析】(1)根据题意可知当因式false或false的值为0时,多项式false的值为0,由此可得答案;
(2)当false时,false的值为false,由此可判断false是多项式M的一个因式;
(3)根据题意可知false是多项式false的一个因式,结合(1)(2)两问可知当false时,false,由此可得k的值.
【解答】解:(1)∵false,
∴当false或false时,false,
即:当false或false时,false,
故答案为:2或-1;
(2)根据题意可知:false是多项式M的一个因式,
故答案为:多项式M能被false整除;
(3)根据题意可知:当false时,false,
即:当false时,false,
则false,
解得false,
答:k的值为3.
【点评】本题考查了整式的除法,是一道推理题,掌握好整式的除法法则是解题的关键.
45.(1)false,false,false;(2)false;(3)341
【解析】(1)根据平方差公式及多项式乘多项式法则计算即可;
(2)根据(1)的答案归纳总结即可;
(3)利用(2)的规律变形为(2)的形式计算即可.
【解答】解:(1)false,
false
false,
false
false,
故答案为:false,false,false;
(2)根据(1)的结果可知:falsefalse,
故答案为:false;
(3)原式false
falsefalse
false
false
false.
【点评】本题考查了平方差公式及多项式乘以多项式的变化规律,弄清题中的规律是解本题的关键.
