11.2.1:三角形的内角 同步提高课时练习(含解析)
文档属性
| 名称 | 11.2.1:三角形的内角 同步提高课时练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 899.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 00:00:00 | ||
图片预览



文档简介
11.2.1:三角形的内角
1.适合条件∠A=∠B=false∠C的三角形一定是( )
A.锐角三角形; B.钝角三角形; C.直角三角形; D.任意三角形.
2.一个三角形三个内角的度数之比为2∶3∶7,这个三角形一定是( )
A.等腰三角形 B.直角三角形 C.锐角三角形 D.钝角三角形
3.下列条件中,能判定△ABC为直角三角形的是( )
A.∠A=2∠B=3∠C B.∠A+∠B=2∠C
C.∠A=∠B=30° D.∠A=false∠B=false∠C
4.如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为( )
A.65° B.55° C.45° D.35°
5.如图所示,一个60o角的三角形纸片,剪去这个60°角后,得到 一个四边形,则么的度数为( )
A.120O B.180O. C.240O D.3000
6.在△ABC中,∠A:∠B:∠C=1:2:3,则△ABC为( )
A.等腰三角形 B.锐角三角形 C.直角三角形 D.钝角三角形
7.如图,在△ABC中,∠B=50°,∠A=30°,CD平分∠ACB,CE⊥AB于点E,则∠DCE的度数是( )
A.5° B.8° C.10° D.15°
8.下列命题是假命题的是( )
A.同角(或等角)的余角相等
B.三角形的任意两边之和大于第三边
C.三角形的内角和为180°
D.两直线平行,同旁内角相等
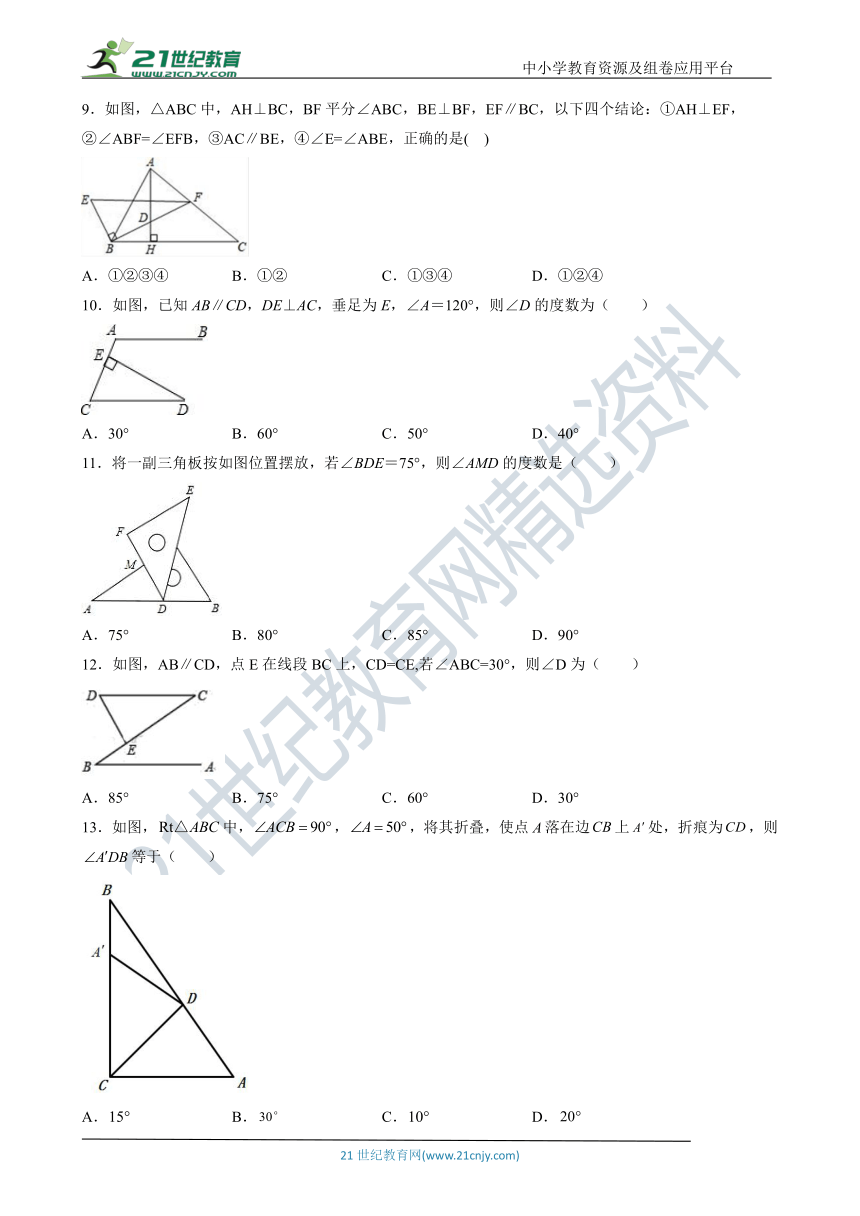
9.如图,△ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC,以下四个结论:①AH⊥EF,②∠ABF=∠EFB,③AC∥BE,④∠E=∠ABE,正确的是( )
A.①②③④ B.①② C.①③④ D.①②④
10.如图,已知AB∥CD,DE⊥AC,垂足为E,∠A=120°,则∠D的度数为( )
A.30° B.60° C.50° D.40°
11.将一副三角板按如图位置摆放,若∠BDE=75°,则∠AMD的度数是( )
A.75° B.80° C.85° D.90°
12.如图,AB∥CD,点E在线段BC上,CD=CE,若∠ABC=30°,则∠D为( )
A.85° B.75° C.60° D.30°
13.如图,false中,false,false,将其折叠,使点false落在边false上false处,折痕为false,则false等于( )
A.false B.false C.false D.false
14.下列能判定三角形是等腰三角形的是(? ?)
A.有两个角为30°、60°?? B.有两个角为40°、80°
C.有两个角为50°、80°?? D.有两个角为100°、120°
15.如图,AD是△ABC的高,BE是△ABC的角平分线,BE,AD相交于点F,已知∠BAD=42°,则∠BFD=( )
A.45° B.54° C.56° D.66°
16.如图,五边形false中,false,false、false、false是false、false、false的外角,则false等于( )
A.90° B.180° C.150° D.120°
17.已知false是锐角三角形,false, 则false的度数可以是( )
A.false B.false C.false D.false
18.若△ABC内有一个点P1,当P1、A、B、C没有任何三点在同一直线上时,如图1,可构成3个互不重叠的小三角形;若△ABC内有两个点P1、P2,其它条件不变,如图2,可构成5个互不重叠的小三角形:……若△ABC内有n个点,其它条件不变,则构成若干个互不重叠的小三角形,这些小三角形的内角和为()
A.n·180° B.(n+2)·180° C.(2n-1)·180° D.(2n+1)·180°
19.如图,在false中,点false是false上的点,false,将false沿着false翻折得到false,则false______°.
20.如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点,将Rt△ABC沿CD折叠,使点B落在AC边上的B′处,则∠ADB′等于_____.
21.如图,AD、AE分别是△ABC的角平分线和高,∠B=50°,∠C=70°,则∠DAE=_____________°.
22.如图,∠1+∠2+∠3+∠4=______度.
23.如图,在△ABC中,BE平分∠ABC,CE平分∠ACB,∠A=64°,则∠BEC=_____度.
24.直角三角形中,一个锐角等于另一个锐角的2倍,则较小的锐角是_______.
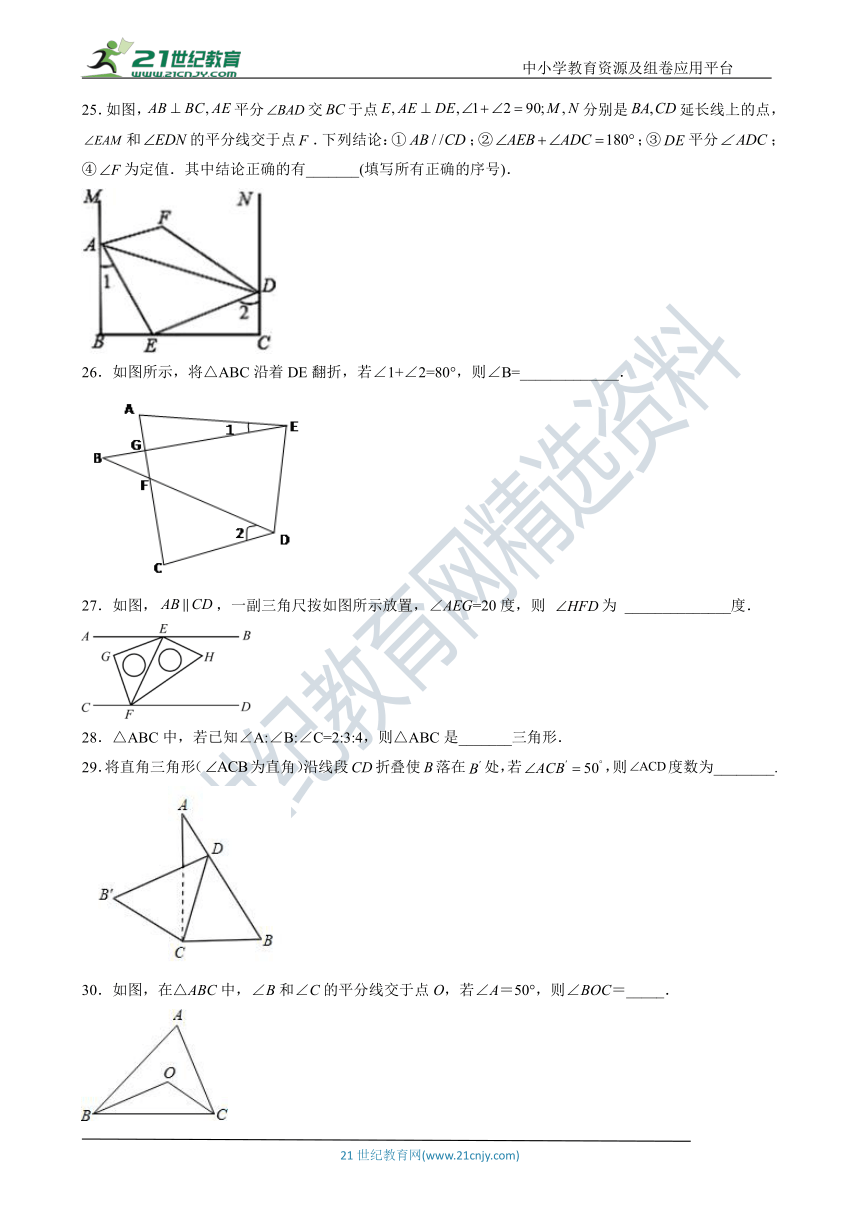
25.如图,false平分false交false于点false分别是false延长线上的点,false和false的平分线交于点false.下列结论:①false;②false;③false平分false;④false为定值.其中结论正确的有_______(填写所有正确的序号).
26.如图所示,将△ABC沿着DE翻折,若∠1+∠2=80°,则∠B=_____________.
27.如图,false,一副三角尺按如图所示放置,∠AEG=20度,则 false为 ______________度.
28.△ABC中,若已知∠A:∠B:∠C=2:3:4,则△ABC是_______三角形.
29.将直角三角形(false为直角)沿线段CD折叠使B落在false处,若false,则false度数为________.
30.如图,在△ABC中,∠B和∠C的平分线交于点O,若∠A=50°,则∠BOC=_____.
31.如图△ABC中,∠ABC、∠ACB的平分线相交于点O,若∠A = 100°,则∠BOC = ____o.
32.已知如图,BQ平分∠ABP,CQ平分∠ACP,∠BAC=α,∠BPC=β,则∠BQC=_________.(用α,β表示)
33.如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=50°,求∠DAC及∠BOA的度数.
34.如图,在四边形false中,false,false,false,且false,false,求false的度数.
35.如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
36.如图,在△ABC中,∠B=40°,∠C=80°,AD是BC边上的高,AE平分∠BAC,
(1)求∠BAE的度数;(2)求∠DAE的度数.
37.如图,在△ ABC中,∠ ABC、∠ ACB的平分线交于点O.
(1)若∠ABC=40°,∠ ACB=50°,则∠BOC=_______
(2)若∠ABC+∠ ACB=lO0°,则∠BOC="________"
(3)若∠A=70°,则∠BOC=_________
(4)若∠BOC=140°,则∠A=________
(5)你能发现∠ BOC与∠ A之间有什么数量关系吗?写出并说明理由.
38.如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B,求证:CD⊥AB.
39.如图,已知直线false,false平分false,交false于点false,false,求false的度数.
40.已知:如图,false求证:false.
41.如图①,点false是false的边false上一点,连结false把false沿false折叠,使点false落在false处,令false.
(1)如图②,当点false落在四边形false内部时,若false,则false的度数为 ;
(2)事实上,当点false落在四边形false内部时,false与false之间的数量关系始终保持不变,请写出false与false之间的数量关系,并利用图②进行证明;
(3)如图③,当点false落在四边形false外部时,直接写出false与false之间的数量关系为 .
42.将一块直角三角板false放置在锐角false上,使得该三角板的两条直角边false恰好分别经过点false
(1)如图①,若false时,点false在false内,则false 度,false____度,false 度;
(2)如图②,改变直角三角板false的位置,使点false在false内,请探究false与false之间存在怎样的数量关系,并验证你的结论;
(3)如图③,改变直角三角板false的位置,使点false在false外,且在false边的左侧,直接写出false三者之间存在的数量关系.
43.如图.在false中,false平分false交false于点false,过点false作false交false于点false,false,求false的度数.
44.如图:点C在线段BD上,AC⊥CE,∠A=∠1,∠E=∠2.
(1)若∠1=70°,求∠B、∠D的度数;
(2)判断AB与ED的位置关系,并说明理由;
(3)作∠A、∠E的角平分线相交于点P,求∠P的度数.
参考答案
1.B
【解答】试题分析:设∠A=x,则∠B=x,∠C=3x.根据三角形的内角和定理,得:x+x+3x=180°,x=36°,则∠C=108°,所以该三角形是钝角三角形.故选B.
考点:三角形内角和定理.
2.D
【解答】试题解析:∵一个三角形三个内角的度数之比为2:3:7,
∴这个三角形的最大角为:180°×false=105°,
∴这个三角形一定是钝角三角形.
故选D
3.D
【解析】
试题解析:A、∠A+∠B+∠C=180°,而∠A=2∠B=3∠C,则∠A=false,所以A选项错误;
B、∠A+∠B+∠C=180°,而∠A+∠B=2∠C,则∠C=60°,不能确定△ABC为直角三角形,所以B选项错误;
C、∠A+∠B+∠C=180°,而∠A=∠B=30°,则∠C=120°,所以B选项错误;
D、∠A+∠B+∠C=180°,而∠A=false∠B=false∠C,则∠C=90°,所以D选项正确.
故选D.
考点:三角形内角和定理.
4.B
【解答】试题分析:由DA⊥AC,∠ADC=35°,可得∠ACD=55°,根据两线平行,同位角相等即可得∵AB∥CD,∠1=∠ACD=55°,故答案选B.
考点:平行线的性质.
5.C
【解答】如图,根据三角形内角和定理,得∠3+∠4+600=1800,
又根据平角定义,∠1+∠3=1800,∠2+∠4=1800,
∴1800-∠1+1800-∠2+600=1800.
∴∠1+∠2=240O.
故选C.
6.C
【解析】设∠A=x,则∠B=2x,∠C=3x,再根据三角形内角和定理求出x的值,进而可得出结论.
【解答】∵在△ABC中,若∠A:∠B:∠C=1:2:3,
∴设∠A=x,则∠B=2x,∠C=3x,
∴x+2x+3x=180°,解得x=30°,
∴∠C=3x=90°,
∴此三角形是直角三角形.
故选:C.
【点评】本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.
7.C
【解析】依据直角三角形,即可得到∠BCE=40°,再根据∠A=30°,CD平分∠ACB,即可得到∠BCD的度数,再根据∠DCE=∠BCD﹣∠BCE进行计算即可.
【解答】∵∠B=50°,CE⊥AB,
∴∠BCE=40°,
又∵∠A=30°,CD平分∠ACB,
∴∠BCD=false∠BCA=false×(180°﹣50°﹣30°)=50°,
∴∠DCE=∠BCD﹣∠BCE=50°﹣40°=10°,
故选C.
【点评】本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.
8.D
【解析】
【解析】利用余角的定义、三角形的三边关系、三角形的内角和及平行线的性质分别判断后即可确定正确的选项.
【解答】A、同角(或等角)的余角相等,正确,是真命题;
B、三角形的任意两边之和大于第三边,正确,是真命题;
C、三角形的内角和为180°,正确,是真命题;
D、两直线平行,同旁内角互补,故错误,是假命题,
故选D.
【点评】考查了命题与定理的知识,解题的关键是了解余角的定义、三角形的三边关系、三角形的内角和及平行线的性质,难度不大.
9.D
【解答】解:∵AH⊥BC,EF∥BC,
∴①AH⊥EF正确;
∵BF平分∠ABC,
∴∠ABF=∠CBF,
∵EF∥BC,
∴∠EFB=∠CBF,
∴②∠ABF=∠EFB正确;
∵BE⊥BF,而AC与BF不一定垂直,
∴BE∥AC不一定成立,故③错误;
∵BE⊥BF,
∴∠E和∠EFB互余,∠ABE和∠ABF互余,而∠EFB=∠ABF,
∴④∠E=∠ABE正确.
故选D.
10.A
【解析】
分析:根据平行线的性质求出∠C,求出∠DEC的度数,根据三角形内角和定理求出∠D的度数即可.
详解:∵AB∥CD,∴∠A+∠C=180°.
∵∠A=120°,∴∠C=60°.
∵DE⊥AC,∴∠DEC=90°,∴∠D=180°﹣∠C﹣∠DEC=30°.
故选A.
点睛:本题考查了平行线的性质和三角形内角和定理的应用,能根据平行线的性质求出∠C的度数是解答此题的关键.
11.D
【解析】根据已知,求出∠ADF,便可找到答案了.
【解答】解:∵∠B=60°,
∴∠A=30°,
∵∠BDE=75°,∠FDE=45°,
∴∠ADF=180°﹣75°﹣45°=60°,
∴∠AMD=180°﹣30°﹣60°=90°,
故选:D.
【点评】本题考查三角板当中的特殊性,以及三角形内角和性质。能够结合具体分析即可.
12.B
【解答】分析:先由AB∥CD,得∠C=∠ABC=30°,CD=CE,得∠D=∠CED,再根据三角形内角和定理得,∠C+∠D+∠CED=180°,即30°+2∠D=180°,从而求出∠D.
详解:∵AB∥CD,
∴∠C=∠ABC=30°,
又∵CD=CE,
∴∠D=∠CED,
∵∠C+∠D+∠CED=180°,即30°+2∠D=180°,
∴∠D=75°.
故选B.
点睛:此题考查的是平行线的性质及三角形内角和定理,解题的关键是先根据平行线的性质求出∠C,再由CD=CE得出∠D=∠CED,由三角形内角和定理求出∠D.
13.C
【解析】由三角形的一个外角等于与它不相邻的两个内角的和,得∠A′DB=∠CA'D-∠B,又由于折叠前后图形的形状和大小不变,∠CA'D=∠A=50°,易求∠B=90°-∠A=40°,从而求出∠A′DB的度数.
【解答】∵Rt△ABC中,∠ACB=90°,∠A=50°,
∴∠B=90°-50°=40°,
∵将其折叠,使点A落在边CB上A′处,折痕为CD,则∠CA'D=∠A,
∵∠CA'D是△A'BD的外角,
∴∠A′DB=∠CA'D-∠B=50°-40°=10°.
故选C.
【点评】本题考查图形的折叠变化及三角形的外角性质.关键是要理解折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.解答此题的关键是要明白图形折叠后与折叠前所对应的角相等.
14.C
【解答】A、因为有两个角为30°、60°,则第三个角为90°,所以此选项不正确;
B、因为有两个角为40°、80°,则第三个角为60°,所以此选项不正确;
C、因为有两个角为50°、80°,则第三个角为50°,有两个角相等,所以此选项正确;
D、因为100°+120°>180°,所以此选项不正确;
故选:C.
15.D
【解析】根据三角形内角和定理求出∠ABD,根据角平分线的定义求出∠ABF,根据三角形的外角性质求出即可.
【解答】解:∵AD是△ABC的高,
∴∠ADB=90°,
∵∠BAD=42°,
∴∠ABD=180°﹣∠ADB﹣∠BAD=48°,
∵BE是△ABC的角平分线,
∴∠ABF=false∠ABD=24°,
∴∠BFD=∠BAD+∠ABF=42°+24°=66°,
故选:D.
【点评】本题考查三角形内角和定理、角平分线的定义,解题的关键是熟记概念与定理并准确识图.
16.B
【解析】延长AE与CD交于点F,根据平行线的性质得false,再根据三角形内角和定理即可求解.
【解答】∵AB∥CD,
∴∠B+∠C=180°,
∴∠4+∠5=180°,
根据多边形的外角和定理,∠1+∠2+∠3+∠4+∠5=360°,
∴∠1+∠2+∠3=360°-180°=180°.
故选:B.
【点评】本题考查了五边形的角度问题,掌握平行线的性质、三角形内角和定理是解题的关键.
17.D
【解析】将∠B的度数依次代入false中,根据三角形的内角和为180°即可判断false是否为锐角三角形.
【解答】A.当∠B=false时,false,则∠C=180°-20°-45°=115°,显然不是锐角三角形,故错误;
B.当∠B=false时,false,则∠C=180°-false-45°=105°,显然不是锐角三角形,故错误;
C.当∠B=false时,false,则∠C=180°-false-45°=90°,显然不是锐角三角形,故错误;
D.当∠B=false时,false,则∠C=180°-20°-45°=75°,显然是锐角三角形,故正确;
故选D.
【点评】此题考查三角形的内角和,解题关键在于掌握锐角三角形的特点.
18.D
【解析】当△ABC内的点的个数是1时,三角形内互不重叠的小三角形的个数是3;当△ABC内的点的个数是2时,三角形内互不重叠的小三角形的个数是5;依此类推得到当△ABC内的点的个数是3时,三角形内互不重叠的小三角形的个数是7;当△ABC内的点的个数是n时,三角形内互不重叠的小三角形的个数2n+1,所以这些小三角形的内角和为(2n+1)·180°
【解答】】解:图1中,当△ABC内只有1个点时,可分割成3个互不重叠的小三角形;
图2中,当△ABC内只有2个点时,可分割成5个互不重叠的小三角形;
图3中,当△ABC内只有3个点时,可分割成7个互不重叠的小三角形;
根据以上规律,当△ABC内有n个点(P1,P2,…,Pn)时,可以把△ABC分割成S=2n+1个互不重叠的三角形,所以这些小三角形的内角和为(2n+1)·180°.
【点评】此题考查了平面图形的有规律变化,要求学生通过观察图形,分析、归纳并发现其中的规律,并应用规律解决问题是解题的关键.
19.20
【解析】根据三角形内角和和翻折的性质解答即可.
【解答】解:false,将false沿着false翻折得到false,
false,false,
false,
故答案为20
【点评】此题考查翻折的性质,关键是根据三角形内角和和翻折的性质解答.
20.40°.
【解答】∵将Rt△ABC沿CD折叠,使点B落在AC边上的B′处,
∴∠ACD=∠BCD,∠CDB=∠CDB′,
∵∠ACB=90°,∠A=25°,
∴∠ACD=∠BCD=45°,∠B=90°﹣25°=65°,
∴∠BDC=∠B′DC=180°﹣45°﹣65°=70°,
∴∠ADB′=180°﹣70°﹣70°=40°.
故答案为40°.
21.10
【解析】根据三角形内角和定理求出∠BAC,再根据角平分线的定义求出∠BAD,根据直角三角形两锐角互余求出∠BAE,然后求解即可.
【解答】解:∵∠B=50°,∠C=70°,
∴∠BAC=180°-∠B-∠C=180°-50°-70°=60°,
∵AD是角平分线,
∴∠BAD=false∠BAC=false×60°=30°,
∵AE是高,
∴∠BAE=90°-∠B=90°-50°=40°,
∴∠DAE=∠BAE-∠BAD=40°-30°=10°.
故答案为:10.
【点评】本题考查了三角形的内角和定理,三角形的角平分线、高线的定义,直角三角形两锐角互余的性质,熟记定理并准确识图是解题的关键.
22.280
【解答】根据三角形内角和定理,可得:∠1+∠2=180°-40°=140°,∠3+∠4=180°-40°=140°,则∠1+∠2+∠3+∠4=140°+140°=280°.
故答案为280.
23.122.
【解析】
【解析】根据三角形的内角和定理和角平分线的定义求得.
【解答】∵在△ABC中,BE平分∠ABC,CE平分∠ACB,∠A=64°,
∴∠EBC+∠ECB=false=58°,
∴∠BEC=180°-58°=122°;
故答案为:122.
【点评】本题考查了角平分线的定义,三角形的内角和,熟记三角形的内角和是解题的关键.
24.30°
【解析】设较小的锐角是false,然后根据直角三角形两锐角互余列出方程求解即可.
【解答】设较小的锐角是x,则另一个锐角是2x,
由题意得,x+2x=90°,
解得x=30°,
即此三角形中最小的角是30°.
故答案为30°.
【点评】本题考查了直角三角形的性质,熟练掌握该知识点是本题解题的关键.
25.①③④
【解析】先根据AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,∠EAM和∠EDN的平分线交于点F,由三角形内角和定理以及平行线的性质即可得出结论.
【解答】解:∵AB⊥BC,AE⊥DE,
∴∠1+∠AEB=90°,∠DEC+∠AEB=90°,
∴∠1=∠DEC,
又∵∠1+∠2=90°,
∴∠DEC+∠2=90°,
∴∠C=90°,
∴∠B+∠C=180°,
∴AB∥CD,故①正确;
∴∠ADN=∠BAD,
∵∠ADC+∠ADN=180°,
∴∠BAD+∠ADC=180°,
又∵∠AEB≠∠BAD,
∴AEB+∠ADC≠180°,故②错误;
∵∠4+∠3=90°,∠2+∠1=90°,而∠3=∠1,
∴∠2=∠4,
∴ED平分∠ADC,故③正确;
∵∠1+∠2=90°,
∴∠EAM+∠EDN=360°-90°=270°.
∵∠EAM和∠EDN的平分线交于点F,
∴∠EAF+∠EDF=false×270°=135°.
∵AE⊥DE,
∴∠3+∠4=90°,
∴∠FAD+∠FDA=135°-90°=45°,
∴∠F=180°-(∠FAD+∠FDA)=180-45°=135°,故④正确.
故答案为:①③④.
【点评】此题考查平行线的性质与判定、三角形内角和定理、直角三角形的性质及角平分线的性质,熟知三角形的内角和等于180°是解题的关键.
26.40°
【解析】利用三角形的内角和和四边形的内角和即可求得.
【解答】∵△ABC沿着DE翻折,
∴∠1+2∠BED=180°,∠2+2∠BDE=180°,
∴∠1+∠2+2(∠BED+∠BDE)=360°,
而∠1+∠2=80°,∠B+∠BED+∠BDE=180°,
∴80°+2(180°-∠B)=360°,
∴∠B=40°.
故答案为40°.
【点评】本题考查图形的折叠变化及三角形的内角和定理.关键是要理解折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.
27.35
【解析】
分析:过点G作AB平行线交EF于P,根据平行线的性质求出∠EGP,求出∠PGF,根据平行线的性质、平角的概念计算即可.
详解:过点G作AB平行线交EF于P,
由题意易知,AB∥GP∥CD,
∴∠EGP=∠AEG=20°,
∴∠PGF=70°,
∴∠GFC=∠PGF=70°,
∴∠HFD=180°-∠GFC-∠GFP-∠EFH=35°.
故答案为35°.
点睛:本题考查的是平行线的性质、三角形内角和定理的应用,掌握两直线平行、内错角相等是解题的关键.
28.锐角.
【解析】
试题解析:已知在△ABC中,∠A:∠B:∠C=2:3:4,
设∠A=2x,根据三角形的内角和定理,
则得到方程2x+3x+4x=180°,
解得2x=40°.
3x=60°,4x=80°.
则△ABC是锐角三角形.
考点:三角形内角和定理.
29.20°.
【解析】根据翻折的性质可知:∠BCD=∠B′CD,又∠BCD+∠B′CD=∠B′CB=∠ACB+∠ACB′=90°+50°=140°,继而即可求出∠BCD的值,又∠ACD+∠BCD=∠ACB=90°,继而即可求出∠ACD的度数.
【解答】解:∵△B′CD时由△BCD翻折得到的,
∴∠BCD=∠B′CD,
又∵∠BCD+∠B′CD=∠B′CB=∠ACB+∠ACB′=90°+50°=140°,
∴∠BCD=70°,
又∵∠ACD+∠BCD=∠ACB=90°,
∴∠ACD=20°.
故答案为:20°.
【点评】本题考查翻折变换的知识,难度适中,解题关键是掌握折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
30.115°.
【解析】根据三角形的内角和定理得出∠ABC+∠ACB=130°,然后根据角平分线的概念得出∠OBC+∠OCB,再根据三角形的内角和定理即可得出∠BOC的度数.
【解答】解;∵∠A=50°,
∴∠ABC+∠ACB=180°﹣50°=130°,
∵∠B和∠C的平分线交于点O,
∴∠OBC=false∠ABC,∠OCB=false∠ACB,
∴∠OBC+∠OCB=false×(∠ABC+∠ACB)=false×130°=65°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=115°,
故答案为:115°.
【点评】本题考查了三角形的内角和定理和三角形的角平分线的概念,关键是求出∠OBC+∠OCB的度数.
31.140
【解析】根据三角形内角和定理得false,再根据角平分线的性质可得false,最后根据三角形内角和定理即可求出∠BOC的度数.
【解答】∵∠A = 100°
∴false
∵∠ABC、∠ACB的平分线相交于点O
∴false
∴false
故答案为:140.
【点评】本题考查了角平分线相关的计算题,掌握三角形内角和定理、角平分线的性质是解题的关键.
32.false(α+β).
【解析】连接BC,根据角平分线的性质得到∠3=false∠ABP,∠4=false∠ACP,根据三角形的内角和得到∠1+∠2=180°-β,2(∠3+∠4)+(∠1+∠2)=180°-α,求出∠3+∠4=false(β-α),根据三角形的内角和即可得到结论.
【解答】解:连接BC,
∵BQ平分∠ABP,CQ平分∠ACP,
∴∠3=false∠ABP,∠4=false∠ACP,
∵∠1+∠2=180°-β,2(∠3+∠4)+(∠1+∠2)=180°-α,
∴∠3+∠4=false(β-α),
∵∠BQC=180°-(∠1+∠2)-(∠3+∠4)=180°-(180°-β)-false(β-α),
即:∠BQC=false(α+β).
故答案为:false(α+β).
【点评】本题考查了三角形的内角和,角平分线的定义,连接BC构造三角形是解题的关键.
33.∠DAC=40°,∠BOA=115°
【解析】
试题分析:在Rt△ACD中,根据两锐角互余得出∠DAC度数;△ABC中由内角和定理得出∠ABC度数,再根据AE,BF是角平分线可得∠BAO、∠ABO,最后在△ABO中根据内角和定理可得答案.
解:∵AD是BC边上的高,
∴∠ADC=90°,
又∵∠C=50°,
∴在△ACD中,∠DAC=90°-∠C=40°,
∵∠BAC=60°,∠C=50°,
∴在△ABC中,∠ABC=180°-∠BAC-∠C=70°,
又∵AE、BF分别是∠BAC 和∠ABC的平分线,
∴∠BAO=false∠BAC=30°,∠ABO=false∠ABC=35°,
∴∠BOA=180°-∠BAO -∠ABO =180°-30°-35°=115°.
34.false
【解析】连接BD,根据false,可得false,false,由false,false,可得false,即可求解.
【解答】解:如图,连接BD,
∵false,∠C=90°
∴false,false;
∵false,false,
∴false,false,false,
∴△ABD是直角三角形,且false,
又∵false,
∴false,
∴false.
故答案为false.
【点评】本题主要考查四边形的应用,灵活应用勾股定理及其逆定理,是解题的关键.
35.(1) 65°;(2) 25°.
【解答】分析:(1)先根据直角三角形两锐角互余求出∠ABC=90°﹣∠A=50°,由邻补角定义得出∠CBD=130°.再根据角平分线定义即可求出∠CBE=false∠CBD=65°;
(2)先根据直角三角形两锐角互余的性质得出∠CEB=90°﹣65°=25°,再根据平行线的性质即可求出∠F=∠CEB=25°.
详解:
(1)∵在Rt△ABC中,∠ACB=90°,∠A=40°,
∴∠ABC=90°﹣∠A=50°,
∴∠CBD=130°.
∵BE是∠CBD的平分线,
∴∠CBE=false∠CBD=65°;
(2)∵∠ACB=90°,∠CBE=65°,
∴∠CEB=90°﹣65°=25°.
∵DF∥BE,
∴∠F=∠CEB=25°.
点睛:本题考查了三角形内角和定理,直角三角形两锐角互余的性质,平行线的性质,邻补角定义,角平分线定义.掌握各定义与性质是解题的关键.
36.(1) ∠BAE=30 °;(2) ∠EAD=20°.
【解答】分析:
(1)由三角形内角和为180°结合已知条件易得∠BAC=60°,再结合AE平分∠BAC即可得到∠BAE=30°;
(2)由AD是△ABC的高可得∠ADB=90°,结合∠ABC=40°可得∠BAD=50°,再结合∠BAE=30°即可解得∠DAE=20°.
详解:
(1)∵在△ABC中,∠ABC=40°,∠ACB=80°,
∴∠BAC=180°-40°-80°=60°,
∵AE平分∠BAC,
∴∠BAE=30°;
(2)∵AD是△ABC的高,
∴∠ADB=90°,
∴∠BAD=180°-90°-40°=50°,
∴∠DAE=∠BAD-∠BAE=50°-30°=20°.
点睛:这是一道有关三角形角度的几何计算题,熟悉“三角形内角和为180°,三角形高的定义和三角形角平分线的定义”是解答本题的关键.
37.(1)、135°;(2)、130°;(3)、125°;(4)、100°;(5)、∠BOC=90°+0.5∠A
【解析】根据角平分线的性质以及三角形内角和定理得出∠OBC和∠OCB与∠A之间的关系,然后根据△BOC的内角和定理得出∠BOC与∠A的关系.
【解答】(1)∵∠ABC=40°,∠ACB=50°,在△ABC中,∠ABC、∠ACB的平分线交于点O.
∴∠OBC=false∠ABC=20°,∠OCB=false∠ACB=25°,
∴∠BOC=180°-∠OBC-∠OCB=180°-20°-25°=135°,
故答案是:135°;
(2)在△ABC中,∠ABC、∠ACB的平分线交于点O.
∴∠OBC=false∠ABC,∠OCB=false∠ACB,
∴∠OBC+∠OCB=false(∠ABC+∠ACB)=50°,
∴∠BOC=180°-false(∠ABC+∠ACB)=180°-50°=130°,
故答案是130°.
(3)在△ABC中,∠ABC、∠ACB的平分线交于点O.
∴∠OBC=false∠ABC,∠OCB=false∠ACB,
∴∠OBC+∠OCB=false(∠ABC+∠ACB)=55°,
∴∠BOC=180°-false(∠ABC+∠ACB)=180°-55°=125°,
故答案是125°;
(4)∵∠BOC=140°,
∴∠OBC+OCB=40°,
∵∠OBC=false∠ABC,∠OCB=false∠ACB,
∴∠ABC+∠ACB=2(∠OBC+OCB)=80°,
∴∠A=100°,
故答案是:100°;
(5)、BO平分∠ABC, CO平分∠ABC
∴∠OBC=0.5∠ABC ∠OCB=0.5∠ACB
∴∠OBC+∠OCB=0.5∠ABC+0.5∠ACB=
0.5(180-∠A)=90-0.5∠A
∴∠O=180-(∠OBC+∠OCB)=180-(90-0.5∠A)=90°+0.5∠A
38.证明过程见解析
【解答】试题分析:由false可得false, 由false,根据等量代换可得false,从而false,接下来,依据垂线的定义可得到AB和CD的位置关系.
证明:在false中,false,
∴false,
又∵false,
∴false,
∴false,
∴false.
点睛:本题主要就是依据三角形的内角和定理和垂线的定义求解的. 当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线.
39.100°
【解析】根据平行线的性质可得false,再根据角平分线的性质可得false,最后根据三角形内角和定理求解即可.
【解答】∵false
∴false
∵false
∴false
∵false平分false
∴false
∴false
【点评】本题考查了平行线的角度问题,掌握平行线的性质、角平分线的性质、三角形内角和定理是解题的关键.
40.见解析
【解析】根据平行线的性质得到∠DAB+∠B=∠BCD+∠D=180°,∠2=∠3,等量代换得到∠DAB=∠BCD,根据对顶角的性质得到∠1=∠2,∠3=∠4,等量代换得到∠1=∠4,根据三角形的外角的性质得到∠E=∠DAB-∠1,∠F=∠BCD-∠4,于是得到结论.
【解答】如下图:
∵AD∥BC,
∴∠DAB+∠B=∠BCD+∠D=180°,∠2=∠3,
∵∠B=∠D,
∴∠DAB=∠BCD,
∵∠1=∠2,∠3=∠4,
∴∠1=∠4,
∴∠E=∠DAB-∠1,∠F=∠BCD-∠4,
∴∠E=∠F.
【点评】此题主要查了平行线的性质与判定以及三角形内角和定理等知识,熟练正确平行线的性质是解决问题的关键.
41.(1)false;(2)false,证明见解析;(3)false.
【解析】(1)根据翻折变换的性质用∠1、∠2表示出∠ADE和∠AED,再根据三角形的内角和定理列式整理即可得解;
(2)设false,分别用含α和β的式子表示出false、false和false,求出false即可得解;
(3)设false,分别用含α和β的式子表示出false、false和false,分别对式子变形整理可得答案.
【解答】解:(1)由折叠的性质得:∠ADE=∠A′DE,∠AED=∠A′ED,false,
∴∠ADE=false(180°?∠1),∠AED=false(180°?∠2),
在△ADE中,∠A+∠ADE+∠AED=180°,
∴30°+false(180°?∠1)+false(180°?∠2)=180°,
整理得:∠1+∠2=60°;
(2)设false,则false,false,
∴false,
由false和false得:false,即false;
(3)设false,则false,false,
∴false,false
∵false,即false.
【点评】本题考查了翻折变换的性质,三角形内角和定理,难度不大,熟记性质并准确识图是解题的关键.
42.(1)135;90;45;(2)∠ABD+∠ACD=90°-∠A,证明见解析;(3)∠ACD-∠ABD=90°-∠A
【解析】(1)在△BCD中,根据三角形内角和定理可得∠DBC+∠DCB =90°,在△ABC中,根据三角形内角和定理可得∠ABC+∠ACB=135°,进而可求出∠ABD+∠ACD的度数;
(2)根据三角形内角和定理可得∠ABC+∠ACB=180°-∠A,∠DBC+∠DCB=90°,
整理可得∠ABD+∠ACD=90°-∠A;
(3)根据三角形内角和定理可得∠ACD+∠A+∠AMC=180°,∠ABD+∠D+∠BMD=180°,整理可得∠ACD-∠ABD=90°-∠A.
【解答】解:(1)在△ABC中,∵∠A=45°,
∴∠ABC+∠ACB=180°-45°=135°,
在△DBC中,∵∠BDC=90°,
∴∠DBC+∠DCB=180°-90°=90°,
∴∠ABD+∠ACD=135°-90°=45°;
故答案为:135;90;45.?
(2)∠ABD+∠ACD与∠A之间的数量关系为:∠ABD+∠ACD=90°-∠A.证明如下:
在△ABC中,∠ABC+∠ACB=180°-∠A.?
在△DBC中,∠DBC+∠DCB=90°.
∴∠ABC+∠ACB-(∠DBC+∠DCB)=180°-∠A-90°.
∴∠ABD+∠ACD=90°-∠A.
(3)∠ACD-∠ABD=90°-∠A.
如图③,设AB交CD于点M,
∵∠ACD+∠A+∠AMC=180°,∠ABD+∠D+∠BMD=180°,∠AMC=∠BMD,
∴∠ACD-∠ABD=90°-∠A.
【点评】本题考查了三角形的内角和定理,对顶角相等,熟练掌握三角形内角和是180°是解答本题的关键.
43.∠CDE =39°
【解析】利用三角形的内角和定理求出∠ACB,再利用角平分线的定义求出∠BCD,利用平行线的性质即可解决问题.
【解答】解:∵CD平分∠ACB,
∴∠BCD=false∠ACB,
∵∠ACB=180°-∠A-∠B=180°-54°-48°=78°,
∴∠BCD=39°,
∵DE//BC,
∴∠CDE=∠BCD=39°.
【点评】本题考查三角形内角和定理,角平分线的定义,平行线的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
44.(1)false,false;(2)false,证明见解析;(3)false.
【解析】(1)由三角形内角和及已知直接可求∠B ,再AC⊥CE可得false,求出∠2,同理可求∠D.
(2)由已知易得false,从而可得false,根据平行线的判定定理得到:直线false与false平行.
(3)由AP、EP是∠BAC、∠CED的角平分线可得false,再由三角形内角和定理可求false,进而可得false,再由三角形内角和即可求解.
【解答】解:(1)∵∠A=∠1,∠1=70°,
在false中,false,
∴false,
又false,
∴false,
又∵false,false,
false.
(2)false;理由如下:
false,
∴false,
又∵∠A=∠1,∠E=∠2.
∴false
∴false,
又∵false,
false,
false.
(3)如图,连接AE,
由(2)可知false,
∵AP、EP平分false、false,即false,false
∴false,
false,
∴false,
∴false,
∴false,
即:false.
【点评】该题主要考查了三角形内角和及平行线的判定等问题;灵活运用三角形的内角和定理求解是解题的关键.
1.适合条件∠A=∠B=false∠C的三角形一定是( )
A.锐角三角形; B.钝角三角形; C.直角三角形; D.任意三角形.
2.一个三角形三个内角的度数之比为2∶3∶7,这个三角形一定是( )
A.等腰三角形 B.直角三角形 C.锐角三角形 D.钝角三角形
3.下列条件中,能判定△ABC为直角三角形的是( )
A.∠A=2∠B=3∠C B.∠A+∠B=2∠C
C.∠A=∠B=30° D.∠A=false∠B=false∠C
4.如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为( )
A.65° B.55° C.45° D.35°
5.如图所示,一个60o角的三角形纸片,剪去这个60°角后,得到 一个四边形,则么的度数为( )
A.120O B.180O. C.240O D.3000
6.在△ABC中,∠A:∠B:∠C=1:2:3,则△ABC为( )
A.等腰三角形 B.锐角三角形 C.直角三角形 D.钝角三角形
7.如图,在△ABC中,∠B=50°,∠A=30°,CD平分∠ACB,CE⊥AB于点E,则∠DCE的度数是( )
A.5° B.8° C.10° D.15°
8.下列命题是假命题的是( )
A.同角(或等角)的余角相等
B.三角形的任意两边之和大于第三边
C.三角形的内角和为180°
D.两直线平行,同旁内角相等
9.如图,△ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC,以下四个结论:①AH⊥EF,②∠ABF=∠EFB,③AC∥BE,④∠E=∠ABE,正确的是( )
A.①②③④ B.①② C.①③④ D.①②④
10.如图,已知AB∥CD,DE⊥AC,垂足为E,∠A=120°,则∠D的度数为( )
A.30° B.60° C.50° D.40°
11.将一副三角板按如图位置摆放,若∠BDE=75°,则∠AMD的度数是( )
A.75° B.80° C.85° D.90°
12.如图,AB∥CD,点E在线段BC上,CD=CE,若∠ABC=30°,则∠D为( )
A.85° B.75° C.60° D.30°
13.如图,false中,false,false,将其折叠,使点false落在边false上false处,折痕为false,则false等于( )
A.false B.false C.false D.false
14.下列能判定三角形是等腰三角形的是(? ?)
A.有两个角为30°、60°?? B.有两个角为40°、80°
C.有两个角为50°、80°?? D.有两个角为100°、120°
15.如图,AD是△ABC的高,BE是△ABC的角平分线,BE,AD相交于点F,已知∠BAD=42°,则∠BFD=( )
A.45° B.54° C.56° D.66°
16.如图,五边形false中,false,false、false、false是false、false、false的外角,则false等于( )
A.90° B.180° C.150° D.120°
17.已知false是锐角三角形,false, 则false的度数可以是( )
A.false B.false C.false D.false
18.若△ABC内有一个点P1,当P1、A、B、C没有任何三点在同一直线上时,如图1,可构成3个互不重叠的小三角形;若△ABC内有两个点P1、P2,其它条件不变,如图2,可构成5个互不重叠的小三角形:……若△ABC内有n个点,其它条件不变,则构成若干个互不重叠的小三角形,这些小三角形的内角和为()
A.n·180° B.(n+2)·180° C.(2n-1)·180° D.(2n+1)·180°
19.如图,在false中,点false是false上的点,false,将false沿着false翻折得到false,则false______°.
20.如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点,将Rt△ABC沿CD折叠,使点B落在AC边上的B′处,则∠ADB′等于_____.
21.如图,AD、AE分别是△ABC的角平分线和高,∠B=50°,∠C=70°,则∠DAE=_____________°.
22.如图,∠1+∠2+∠3+∠4=______度.
23.如图,在△ABC中,BE平分∠ABC,CE平分∠ACB,∠A=64°,则∠BEC=_____度.
24.直角三角形中,一个锐角等于另一个锐角的2倍,则较小的锐角是_______.
25.如图,false平分false交false于点false分别是false延长线上的点,false和false的平分线交于点false.下列结论:①false;②false;③false平分false;④false为定值.其中结论正确的有_______(填写所有正确的序号).
26.如图所示,将△ABC沿着DE翻折,若∠1+∠2=80°,则∠B=_____________.
27.如图,false,一副三角尺按如图所示放置,∠AEG=20度,则 false为 ______________度.
28.△ABC中,若已知∠A:∠B:∠C=2:3:4,则△ABC是_______三角形.
29.将直角三角形(false为直角)沿线段CD折叠使B落在false处,若false,则false度数为________.
30.如图,在△ABC中,∠B和∠C的平分线交于点O,若∠A=50°,则∠BOC=_____.
31.如图△ABC中,∠ABC、∠ACB的平分线相交于点O,若∠A = 100°,则∠BOC = ____o.
32.已知如图,BQ平分∠ABP,CQ平分∠ACP,∠BAC=α,∠BPC=β,则∠BQC=_________.(用α,β表示)
33.如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=50°,求∠DAC及∠BOA的度数.
34.如图,在四边形false中,false,false,false,且false,false,求false的度数.
35.如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
36.如图,在△ABC中,∠B=40°,∠C=80°,AD是BC边上的高,AE平分∠BAC,
(1)求∠BAE的度数;(2)求∠DAE的度数.
37.如图,在△ ABC中,∠ ABC、∠ ACB的平分线交于点O.
(1)若∠ABC=40°,∠ ACB=50°,则∠BOC=_______
(2)若∠ABC+∠ ACB=lO0°,则∠BOC="________"
(3)若∠A=70°,则∠BOC=_________
(4)若∠BOC=140°,则∠A=________
(5)你能发现∠ BOC与∠ A之间有什么数量关系吗?写出并说明理由.
38.如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B,求证:CD⊥AB.
39.如图,已知直线false,false平分false,交false于点false,false,求false的度数.
40.已知:如图,false求证:false.
41.如图①,点false是false的边false上一点,连结false把false沿false折叠,使点false落在false处,令false.
(1)如图②,当点false落在四边形false内部时,若false,则false的度数为 ;
(2)事实上,当点false落在四边形false内部时,false与false之间的数量关系始终保持不变,请写出false与false之间的数量关系,并利用图②进行证明;
(3)如图③,当点false落在四边形false外部时,直接写出false与false之间的数量关系为 .
42.将一块直角三角板false放置在锐角false上,使得该三角板的两条直角边false恰好分别经过点false
(1)如图①,若false时,点false在false内,则false 度,false____度,false 度;
(2)如图②,改变直角三角板false的位置,使点false在false内,请探究false与false之间存在怎样的数量关系,并验证你的结论;
(3)如图③,改变直角三角板false的位置,使点false在false外,且在false边的左侧,直接写出false三者之间存在的数量关系.
43.如图.在false中,false平分false交false于点false,过点false作false交false于点false,false,求false的度数.
44.如图:点C在线段BD上,AC⊥CE,∠A=∠1,∠E=∠2.
(1)若∠1=70°,求∠B、∠D的度数;
(2)判断AB与ED的位置关系,并说明理由;
(3)作∠A、∠E的角平分线相交于点P,求∠P的度数.
参考答案
1.B
【解答】试题分析:设∠A=x,则∠B=x,∠C=3x.根据三角形的内角和定理,得:x+x+3x=180°,x=36°,则∠C=108°,所以该三角形是钝角三角形.故选B.
考点:三角形内角和定理.
2.D
【解答】试题解析:∵一个三角形三个内角的度数之比为2:3:7,
∴这个三角形的最大角为:180°×false=105°,
∴这个三角形一定是钝角三角形.
故选D
3.D
【解析】
试题解析:A、∠A+∠B+∠C=180°,而∠A=2∠B=3∠C,则∠A=false,所以A选项错误;
B、∠A+∠B+∠C=180°,而∠A+∠B=2∠C,则∠C=60°,不能确定△ABC为直角三角形,所以B选项错误;
C、∠A+∠B+∠C=180°,而∠A=∠B=30°,则∠C=120°,所以B选项错误;
D、∠A+∠B+∠C=180°,而∠A=false∠B=false∠C,则∠C=90°,所以D选项正确.
故选D.
考点:三角形内角和定理.
4.B
【解答】试题分析:由DA⊥AC,∠ADC=35°,可得∠ACD=55°,根据两线平行,同位角相等即可得∵AB∥CD,∠1=∠ACD=55°,故答案选B.
考点:平行线的性质.
5.C
【解答】如图,根据三角形内角和定理,得∠3+∠4+600=1800,
又根据平角定义,∠1+∠3=1800,∠2+∠4=1800,
∴1800-∠1+1800-∠2+600=1800.
∴∠1+∠2=240O.
故选C.
6.C
【解析】设∠A=x,则∠B=2x,∠C=3x,再根据三角形内角和定理求出x的值,进而可得出结论.
【解答】∵在△ABC中,若∠A:∠B:∠C=1:2:3,
∴设∠A=x,则∠B=2x,∠C=3x,
∴x+2x+3x=180°,解得x=30°,
∴∠C=3x=90°,
∴此三角形是直角三角形.
故选:C.
【点评】本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.
7.C
【解析】依据直角三角形,即可得到∠BCE=40°,再根据∠A=30°,CD平分∠ACB,即可得到∠BCD的度数,再根据∠DCE=∠BCD﹣∠BCE进行计算即可.
【解答】∵∠B=50°,CE⊥AB,
∴∠BCE=40°,
又∵∠A=30°,CD平分∠ACB,
∴∠BCD=false∠BCA=false×(180°﹣50°﹣30°)=50°,
∴∠DCE=∠BCD﹣∠BCE=50°﹣40°=10°,
故选C.
【点评】本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.
8.D
【解析】
【解析】利用余角的定义、三角形的三边关系、三角形的内角和及平行线的性质分别判断后即可确定正确的选项.
【解答】A、同角(或等角)的余角相等,正确,是真命题;
B、三角形的任意两边之和大于第三边,正确,是真命题;
C、三角形的内角和为180°,正确,是真命题;
D、两直线平行,同旁内角互补,故错误,是假命题,
故选D.
【点评】考查了命题与定理的知识,解题的关键是了解余角的定义、三角形的三边关系、三角形的内角和及平行线的性质,难度不大.
9.D
【解答】解:∵AH⊥BC,EF∥BC,
∴①AH⊥EF正确;
∵BF平分∠ABC,
∴∠ABF=∠CBF,
∵EF∥BC,
∴∠EFB=∠CBF,
∴②∠ABF=∠EFB正确;
∵BE⊥BF,而AC与BF不一定垂直,
∴BE∥AC不一定成立,故③错误;
∵BE⊥BF,
∴∠E和∠EFB互余,∠ABE和∠ABF互余,而∠EFB=∠ABF,
∴④∠E=∠ABE正确.
故选D.
10.A
【解析】
分析:根据平行线的性质求出∠C,求出∠DEC的度数,根据三角形内角和定理求出∠D的度数即可.
详解:∵AB∥CD,∴∠A+∠C=180°.
∵∠A=120°,∴∠C=60°.
∵DE⊥AC,∴∠DEC=90°,∴∠D=180°﹣∠C﹣∠DEC=30°.
故选A.
点睛:本题考查了平行线的性质和三角形内角和定理的应用,能根据平行线的性质求出∠C的度数是解答此题的关键.
11.D
【解析】根据已知,求出∠ADF,便可找到答案了.
【解答】解:∵∠B=60°,
∴∠A=30°,
∵∠BDE=75°,∠FDE=45°,
∴∠ADF=180°﹣75°﹣45°=60°,
∴∠AMD=180°﹣30°﹣60°=90°,
故选:D.
【点评】本题考查三角板当中的特殊性,以及三角形内角和性质。能够结合具体分析即可.
12.B
【解答】分析:先由AB∥CD,得∠C=∠ABC=30°,CD=CE,得∠D=∠CED,再根据三角形内角和定理得,∠C+∠D+∠CED=180°,即30°+2∠D=180°,从而求出∠D.
详解:∵AB∥CD,
∴∠C=∠ABC=30°,
又∵CD=CE,
∴∠D=∠CED,
∵∠C+∠D+∠CED=180°,即30°+2∠D=180°,
∴∠D=75°.
故选B.
点睛:此题考查的是平行线的性质及三角形内角和定理,解题的关键是先根据平行线的性质求出∠C,再由CD=CE得出∠D=∠CED,由三角形内角和定理求出∠D.
13.C
【解析】由三角形的一个外角等于与它不相邻的两个内角的和,得∠A′DB=∠CA'D-∠B,又由于折叠前后图形的形状和大小不变,∠CA'D=∠A=50°,易求∠B=90°-∠A=40°,从而求出∠A′DB的度数.
【解答】∵Rt△ABC中,∠ACB=90°,∠A=50°,
∴∠B=90°-50°=40°,
∵将其折叠,使点A落在边CB上A′处,折痕为CD,则∠CA'D=∠A,
∵∠CA'D是△A'BD的外角,
∴∠A′DB=∠CA'D-∠B=50°-40°=10°.
故选C.
【点评】本题考查图形的折叠变化及三角形的外角性质.关键是要理解折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.解答此题的关键是要明白图形折叠后与折叠前所对应的角相等.
14.C
【解答】A、因为有两个角为30°、60°,则第三个角为90°,所以此选项不正确;
B、因为有两个角为40°、80°,则第三个角为60°,所以此选项不正确;
C、因为有两个角为50°、80°,则第三个角为50°,有两个角相等,所以此选项正确;
D、因为100°+120°>180°,所以此选项不正确;
故选:C.
15.D
【解析】根据三角形内角和定理求出∠ABD,根据角平分线的定义求出∠ABF,根据三角形的外角性质求出即可.
【解答】解:∵AD是△ABC的高,
∴∠ADB=90°,
∵∠BAD=42°,
∴∠ABD=180°﹣∠ADB﹣∠BAD=48°,
∵BE是△ABC的角平分线,
∴∠ABF=false∠ABD=24°,
∴∠BFD=∠BAD+∠ABF=42°+24°=66°,
故选:D.
【点评】本题考查三角形内角和定理、角平分线的定义,解题的关键是熟记概念与定理并准确识图.
16.B
【解析】延长AE与CD交于点F,根据平行线的性质得false,再根据三角形内角和定理即可求解.
【解答】∵AB∥CD,
∴∠B+∠C=180°,
∴∠4+∠5=180°,
根据多边形的外角和定理,∠1+∠2+∠3+∠4+∠5=360°,
∴∠1+∠2+∠3=360°-180°=180°.
故选:B.
【点评】本题考查了五边形的角度问题,掌握平行线的性质、三角形内角和定理是解题的关键.
17.D
【解析】将∠B的度数依次代入false中,根据三角形的内角和为180°即可判断false是否为锐角三角形.
【解答】A.当∠B=false时,false,则∠C=180°-20°-45°=115°,显然不是锐角三角形,故错误;
B.当∠B=false时,false,则∠C=180°-false-45°=105°,显然不是锐角三角形,故错误;
C.当∠B=false时,false,则∠C=180°-false-45°=90°,显然不是锐角三角形,故错误;
D.当∠B=false时,false,则∠C=180°-20°-45°=75°,显然是锐角三角形,故正确;
故选D.
【点评】此题考查三角形的内角和,解题关键在于掌握锐角三角形的特点.
18.D
【解析】当△ABC内的点的个数是1时,三角形内互不重叠的小三角形的个数是3;当△ABC内的点的个数是2时,三角形内互不重叠的小三角形的个数是5;依此类推得到当△ABC内的点的个数是3时,三角形内互不重叠的小三角形的个数是7;当△ABC内的点的个数是n时,三角形内互不重叠的小三角形的个数2n+1,所以这些小三角形的内角和为(2n+1)·180°
【解答】】解:图1中,当△ABC内只有1个点时,可分割成3个互不重叠的小三角形;
图2中,当△ABC内只有2个点时,可分割成5个互不重叠的小三角形;
图3中,当△ABC内只有3个点时,可分割成7个互不重叠的小三角形;
根据以上规律,当△ABC内有n个点(P1,P2,…,Pn)时,可以把△ABC分割成S=2n+1个互不重叠的三角形,所以这些小三角形的内角和为(2n+1)·180°.
【点评】此题考查了平面图形的有规律变化,要求学生通过观察图形,分析、归纳并发现其中的规律,并应用规律解决问题是解题的关键.
19.20
【解析】根据三角形内角和和翻折的性质解答即可.
【解答】解:false,将false沿着false翻折得到false,
false,false,
false,
故答案为20
【点评】此题考查翻折的性质,关键是根据三角形内角和和翻折的性质解答.
20.40°.
【解答】∵将Rt△ABC沿CD折叠,使点B落在AC边上的B′处,
∴∠ACD=∠BCD,∠CDB=∠CDB′,
∵∠ACB=90°,∠A=25°,
∴∠ACD=∠BCD=45°,∠B=90°﹣25°=65°,
∴∠BDC=∠B′DC=180°﹣45°﹣65°=70°,
∴∠ADB′=180°﹣70°﹣70°=40°.
故答案为40°.
21.10
【解析】根据三角形内角和定理求出∠BAC,再根据角平分线的定义求出∠BAD,根据直角三角形两锐角互余求出∠BAE,然后求解即可.
【解答】解:∵∠B=50°,∠C=70°,
∴∠BAC=180°-∠B-∠C=180°-50°-70°=60°,
∵AD是角平分线,
∴∠BAD=false∠BAC=false×60°=30°,
∵AE是高,
∴∠BAE=90°-∠B=90°-50°=40°,
∴∠DAE=∠BAE-∠BAD=40°-30°=10°.
故答案为:10.
【点评】本题考查了三角形的内角和定理,三角形的角平分线、高线的定义,直角三角形两锐角互余的性质,熟记定理并准确识图是解题的关键.
22.280
【解答】根据三角形内角和定理,可得:∠1+∠2=180°-40°=140°,∠3+∠4=180°-40°=140°,则∠1+∠2+∠3+∠4=140°+140°=280°.
故答案为280.
23.122.
【解析】
【解析】根据三角形的内角和定理和角平分线的定义求得.
【解答】∵在△ABC中,BE平分∠ABC,CE平分∠ACB,∠A=64°,
∴∠EBC+∠ECB=false=58°,
∴∠BEC=180°-58°=122°;
故答案为:122.
【点评】本题考查了角平分线的定义,三角形的内角和,熟记三角形的内角和是解题的关键.
24.30°
【解析】设较小的锐角是false,然后根据直角三角形两锐角互余列出方程求解即可.
【解答】设较小的锐角是x,则另一个锐角是2x,
由题意得,x+2x=90°,
解得x=30°,
即此三角形中最小的角是30°.
故答案为30°.
【点评】本题考查了直角三角形的性质,熟练掌握该知识点是本题解题的关键.
25.①③④
【解析】先根据AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,∠EAM和∠EDN的平分线交于点F,由三角形内角和定理以及平行线的性质即可得出结论.
【解答】解:∵AB⊥BC,AE⊥DE,
∴∠1+∠AEB=90°,∠DEC+∠AEB=90°,
∴∠1=∠DEC,
又∵∠1+∠2=90°,
∴∠DEC+∠2=90°,
∴∠C=90°,
∴∠B+∠C=180°,
∴AB∥CD,故①正确;
∴∠ADN=∠BAD,
∵∠ADC+∠ADN=180°,
∴∠BAD+∠ADC=180°,
又∵∠AEB≠∠BAD,
∴AEB+∠ADC≠180°,故②错误;
∵∠4+∠3=90°,∠2+∠1=90°,而∠3=∠1,
∴∠2=∠4,
∴ED平分∠ADC,故③正确;
∵∠1+∠2=90°,
∴∠EAM+∠EDN=360°-90°=270°.
∵∠EAM和∠EDN的平分线交于点F,
∴∠EAF+∠EDF=false×270°=135°.
∵AE⊥DE,
∴∠3+∠4=90°,
∴∠FAD+∠FDA=135°-90°=45°,
∴∠F=180°-(∠FAD+∠FDA)=180-45°=135°,故④正确.
故答案为:①③④.
【点评】此题考查平行线的性质与判定、三角形内角和定理、直角三角形的性质及角平分线的性质,熟知三角形的内角和等于180°是解题的关键.
26.40°
【解析】利用三角形的内角和和四边形的内角和即可求得.
【解答】∵△ABC沿着DE翻折,
∴∠1+2∠BED=180°,∠2+2∠BDE=180°,
∴∠1+∠2+2(∠BED+∠BDE)=360°,
而∠1+∠2=80°,∠B+∠BED+∠BDE=180°,
∴80°+2(180°-∠B)=360°,
∴∠B=40°.
故答案为40°.
【点评】本题考查图形的折叠变化及三角形的内角和定理.关键是要理解折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.
27.35
【解析】
分析:过点G作AB平行线交EF于P,根据平行线的性质求出∠EGP,求出∠PGF,根据平行线的性质、平角的概念计算即可.
详解:过点G作AB平行线交EF于P,
由题意易知,AB∥GP∥CD,
∴∠EGP=∠AEG=20°,
∴∠PGF=70°,
∴∠GFC=∠PGF=70°,
∴∠HFD=180°-∠GFC-∠GFP-∠EFH=35°.
故答案为35°.
点睛:本题考查的是平行线的性质、三角形内角和定理的应用,掌握两直线平行、内错角相等是解题的关键.
28.锐角.
【解析】
试题解析:已知在△ABC中,∠A:∠B:∠C=2:3:4,
设∠A=2x,根据三角形的内角和定理,
则得到方程2x+3x+4x=180°,
解得2x=40°.
3x=60°,4x=80°.
则△ABC是锐角三角形.
考点:三角形内角和定理.
29.20°.
【解析】根据翻折的性质可知:∠BCD=∠B′CD,又∠BCD+∠B′CD=∠B′CB=∠ACB+∠ACB′=90°+50°=140°,继而即可求出∠BCD的值,又∠ACD+∠BCD=∠ACB=90°,继而即可求出∠ACD的度数.
【解答】解:∵△B′CD时由△BCD翻折得到的,
∴∠BCD=∠B′CD,
又∵∠BCD+∠B′CD=∠B′CB=∠ACB+∠ACB′=90°+50°=140°,
∴∠BCD=70°,
又∵∠ACD+∠BCD=∠ACB=90°,
∴∠ACD=20°.
故答案为:20°.
【点评】本题考查翻折变换的知识,难度适中,解题关键是掌握折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
30.115°.
【解析】根据三角形的内角和定理得出∠ABC+∠ACB=130°,然后根据角平分线的概念得出∠OBC+∠OCB,再根据三角形的内角和定理即可得出∠BOC的度数.
【解答】解;∵∠A=50°,
∴∠ABC+∠ACB=180°﹣50°=130°,
∵∠B和∠C的平分线交于点O,
∴∠OBC=false∠ABC,∠OCB=false∠ACB,
∴∠OBC+∠OCB=false×(∠ABC+∠ACB)=false×130°=65°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=115°,
故答案为:115°.
【点评】本题考查了三角形的内角和定理和三角形的角平分线的概念,关键是求出∠OBC+∠OCB的度数.
31.140
【解析】根据三角形内角和定理得false,再根据角平分线的性质可得false,最后根据三角形内角和定理即可求出∠BOC的度数.
【解答】∵∠A = 100°
∴false
∵∠ABC、∠ACB的平分线相交于点O
∴false
∴false
故答案为:140.
【点评】本题考查了角平分线相关的计算题,掌握三角形内角和定理、角平分线的性质是解题的关键.
32.false(α+β).
【解析】连接BC,根据角平分线的性质得到∠3=false∠ABP,∠4=false∠ACP,根据三角形的内角和得到∠1+∠2=180°-β,2(∠3+∠4)+(∠1+∠2)=180°-α,求出∠3+∠4=false(β-α),根据三角形的内角和即可得到结论.
【解答】解:连接BC,
∵BQ平分∠ABP,CQ平分∠ACP,
∴∠3=false∠ABP,∠4=false∠ACP,
∵∠1+∠2=180°-β,2(∠3+∠4)+(∠1+∠2)=180°-α,
∴∠3+∠4=false(β-α),
∵∠BQC=180°-(∠1+∠2)-(∠3+∠4)=180°-(180°-β)-false(β-α),
即:∠BQC=false(α+β).
故答案为:false(α+β).
【点评】本题考查了三角形的内角和,角平分线的定义,连接BC构造三角形是解题的关键.
33.∠DAC=40°,∠BOA=115°
【解析】
试题分析:在Rt△ACD中,根据两锐角互余得出∠DAC度数;△ABC中由内角和定理得出∠ABC度数,再根据AE,BF是角平分线可得∠BAO、∠ABO,最后在△ABO中根据内角和定理可得答案.
解:∵AD是BC边上的高,
∴∠ADC=90°,
又∵∠C=50°,
∴在△ACD中,∠DAC=90°-∠C=40°,
∵∠BAC=60°,∠C=50°,
∴在△ABC中,∠ABC=180°-∠BAC-∠C=70°,
又∵AE、BF分别是∠BAC 和∠ABC的平分线,
∴∠BAO=false∠BAC=30°,∠ABO=false∠ABC=35°,
∴∠BOA=180°-∠BAO -∠ABO =180°-30°-35°=115°.
34.false
【解析】连接BD,根据false,可得false,false,由false,false,可得false,即可求解.
【解答】解:如图,连接BD,
∵false,∠C=90°
∴false,false;
∵false,false,
∴false,false,false,
∴△ABD是直角三角形,且false,
又∵false,
∴false,
∴false.
故答案为false.
【点评】本题主要考查四边形的应用,灵活应用勾股定理及其逆定理,是解题的关键.
35.(1) 65°;(2) 25°.
【解答】分析:(1)先根据直角三角形两锐角互余求出∠ABC=90°﹣∠A=50°,由邻补角定义得出∠CBD=130°.再根据角平分线定义即可求出∠CBE=false∠CBD=65°;
(2)先根据直角三角形两锐角互余的性质得出∠CEB=90°﹣65°=25°,再根据平行线的性质即可求出∠F=∠CEB=25°.
详解:
(1)∵在Rt△ABC中,∠ACB=90°,∠A=40°,
∴∠ABC=90°﹣∠A=50°,
∴∠CBD=130°.
∵BE是∠CBD的平分线,
∴∠CBE=false∠CBD=65°;
(2)∵∠ACB=90°,∠CBE=65°,
∴∠CEB=90°﹣65°=25°.
∵DF∥BE,
∴∠F=∠CEB=25°.
点睛:本题考查了三角形内角和定理,直角三角形两锐角互余的性质,平行线的性质,邻补角定义,角平分线定义.掌握各定义与性质是解题的关键.
36.(1) ∠BAE=30 °;(2) ∠EAD=20°.
【解答】分析:
(1)由三角形内角和为180°结合已知条件易得∠BAC=60°,再结合AE平分∠BAC即可得到∠BAE=30°;
(2)由AD是△ABC的高可得∠ADB=90°,结合∠ABC=40°可得∠BAD=50°,再结合∠BAE=30°即可解得∠DAE=20°.
详解:
(1)∵在△ABC中,∠ABC=40°,∠ACB=80°,
∴∠BAC=180°-40°-80°=60°,
∵AE平分∠BAC,
∴∠BAE=30°;
(2)∵AD是△ABC的高,
∴∠ADB=90°,
∴∠BAD=180°-90°-40°=50°,
∴∠DAE=∠BAD-∠BAE=50°-30°=20°.
点睛:这是一道有关三角形角度的几何计算题,熟悉“三角形内角和为180°,三角形高的定义和三角形角平分线的定义”是解答本题的关键.
37.(1)、135°;(2)、130°;(3)、125°;(4)、100°;(5)、∠BOC=90°+0.5∠A
【解析】根据角平分线的性质以及三角形内角和定理得出∠OBC和∠OCB与∠A之间的关系,然后根据△BOC的内角和定理得出∠BOC与∠A的关系.
【解答】(1)∵∠ABC=40°,∠ACB=50°,在△ABC中,∠ABC、∠ACB的平分线交于点O.
∴∠OBC=false∠ABC=20°,∠OCB=false∠ACB=25°,
∴∠BOC=180°-∠OBC-∠OCB=180°-20°-25°=135°,
故答案是:135°;
(2)在△ABC中,∠ABC、∠ACB的平分线交于点O.
∴∠OBC=false∠ABC,∠OCB=false∠ACB,
∴∠OBC+∠OCB=false(∠ABC+∠ACB)=50°,
∴∠BOC=180°-false(∠ABC+∠ACB)=180°-50°=130°,
故答案是130°.
(3)在△ABC中,∠ABC、∠ACB的平分线交于点O.
∴∠OBC=false∠ABC,∠OCB=false∠ACB,
∴∠OBC+∠OCB=false(∠ABC+∠ACB)=55°,
∴∠BOC=180°-false(∠ABC+∠ACB)=180°-55°=125°,
故答案是125°;
(4)∵∠BOC=140°,
∴∠OBC+OCB=40°,
∵∠OBC=false∠ABC,∠OCB=false∠ACB,
∴∠ABC+∠ACB=2(∠OBC+OCB)=80°,
∴∠A=100°,
故答案是:100°;
(5)、BO平分∠ABC, CO平分∠ABC
∴∠OBC=0.5∠ABC ∠OCB=0.5∠ACB
∴∠OBC+∠OCB=0.5∠ABC+0.5∠ACB=
0.5(180-∠A)=90-0.5∠A
∴∠O=180-(∠OBC+∠OCB)=180-(90-0.5∠A)=90°+0.5∠A
38.证明过程见解析
【解答】试题分析:由false可得false, 由false,根据等量代换可得false,从而false,接下来,依据垂线的定义可得到AB和CD的位置关系.
证明:在false中,false,
∴false,
又∵false,
∴false,
∴false,
∴false.
点睛:本题主要就是依据三角形的内角和定理和垂线的定义求解的. 当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线.
39.100°
【解析】根据平行线的性质可得false,再根据角平分线的性质可得false,最后根据三角形内角和定理求解即可.
【解答】∵false
∴false
∵false
∴false
∵false平分false
∴false
∴false
【点评】本题考查了平行线的角度问题,掌握平行线的性质、角平分线的性质、三角形内角和定理是解题的关键.
40.见解析
【解析】根据平行线的性质得到∠DAB+∠B=∠BCD+∠D=180°,∠2=∠3,等量代换得到∠DAB=∠BCD,根据对顶角的性质得到∠1=∠2,∠3=∠4,等量代换得到∠1=∠4,根据三角形的外角的性质得到∠E=∠DAB-∠1,∠F=∠BCD-∠4,于是得到结论.
【解答】如下图:
∵AD∥BC,
∴∠DAB+∠B=∠BCD+∠D=180°,∠2=∠3,
∵∠B=∠D,
∴∠DAB=∠BCD,
∵∠1=∠2,∠3=∠4,
∴∠1=∠4,
∴∠E=∠DAB-∠1,∠F=∠BCD-∠4,
∴∠E=∠F.
【点评】此题主要查了平行线的性质与判定以及三角形内角和定理等知识,熟练正确平行线的性质是解决问题的关键.
41.(1)false;(2)false,证明见解析;(3)false.
【解析】(1)根据翻折变换的性质用∠1、∠2表示出∠ADE和∠AED,再根据三角形的内角和定理列式整理即可得解;
(2)设false,分别用含α和β的式子表示出false、false和false,求出false即可得解;
(3)设false,分别用含α和β的式子表示出false、false和false,分别对式子变形整理可得答案.
【解答】解:(1)由折叠的性质得:∠ADE=∠A′DE,∠AED=∠A′ED,false,
∴∠ADE=false(180°?∠1),∠AED=false(180°?∠2),
在△ADE中,∠A+∠ADE+∠AED=180°,
∴30°+false(180°?∠1)+false(180°?∠2)=180°,
整理得:∠1+∠2=60°;
(2)设false,则false,false,
∴false,
由false和false得:false,即false;
(3)设false,则false,false,
∴false,false
∵false,即false.
【点评】本题考查了翻折变换的性质,三角形内角和定理,难度不大,熟记性质并准确识图是解题的关键.
42.(1)135;90;45;(2)∠ABD+∠ACD=90°-∠A,证明见解析;(3)∠ACD-∠ABD=90°-∠A
【解析】(1)在△BCD中,根据三角形内角和定理可得∠DBC+∠DCB =90°,在△ABC中,根据三角形内角和定理可得∠ABC+∠ACB=135°,进而可求出∠ABD+∠ACD的度数;
(2)根据三角形内角和定理可得∠ABC+∠ACB=180°-∠A,∠DBC+∠DCB=90°,
整理可得∠ABD+∠ACD=90°-∠A;
(3)根据三角形内角和定理可得∠ACD+∠A+∠AMC=180°,∠ABD+∠D+∠BMD=180°,整理可得∠ACD-∠ABD=90°-∠A.
【解答】解:(1)在△ABC中,∵∠A=45°,
∴∠ABC+∠ACB=180°-45°=135°,
在△DBC中,∵∠BDC=90°,
∴∠DBC+∠DCB=180°-90°=90°,
∴∠ABD+∠ACD=135°-90°=45°;
故答案为:135;90;45.?
(2)∠ABD+∠ACD与∠A之间的数量关系为:∠ABD+∠ACD=90°-∠A.证明如下:
在△ABC中,∠ABC+∠ACB=180°-∠A.?
在△DBC中,∠DBC+∠DCB=90°.
∴∠ABC+∠ACB-(∠DBC+∠DCB)=180°-∠A-90°.
∴∠ABD+∠ACD=90°-∠A.
(3)∠ACD-∠ABD=90°-∠A.
如图③,设AB交CD于点M,
∵∠ACD+∠A+∠AMC=180°,∠ABD+∠D+∠BMD=180°,∠AMC=∠BMD,
∴∠ACD-∠ABD=90°-∠A.
【点评】本题考查了三角形的内角和定理,对顶角相等,熟练掌握三角形内角和是180°是解答本题的关键.
43.∠CDE =39°
【解析】利用三角形的内角和定理求出∠ACB,再利用角平分线的定义求出∠BCD,利用平行线的性质即可解决问题.
【解答】解:∵CD平分∠ACB,
∴∠BCD=false∠ACB,
∵∠ACB=180°-∠A-∠B=180°-54°-48°=78°,
∴∠BCD=39°,
∵DE//BC,
∴∠CDE=∠BCD=39°.
【点评】本题考查三角形内角和定理,角平分线的定义,平行线的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
44.(1)false,false;(2)false,证明见解析;(3)false.
【解析】(1)由三角形内角和及已知直接可求∠B ,再AC⊥CE可得false,求出∠2,同理可求∠D.
(2)由已知易得false,从而可得false,根据平行线的判定定理得到:直线false与false平行.
(3)由AP、EP是∠BAC、∠CED的角平分线可得false,再由三角形内角和定理可求false,进而可得false,再由三角形内角和即可求解.
【解答】解:(1)∵∠A=∠1,∠1=70°,
在false中,false,
∴false,
又false,
∴false,
又∵false,false,
false.
(2)false;理由如下:
false,
∴false,
又∵∠A=∠1,∠E=∠2.
∴false
∴false,
又∵false,
false,
false.
(3)如图,连接AE,
由(2)可知false,
∵AP、EP平分false、false,即false,false
∴false,
false,
∴false,
∴false,
∴false,
即:false.
【点评】该题主要考查了三角形内角和及平行线的判定等问题;灵活运用三角形的内角和定理求解是解题的关键.
